随着无线通信技术的进步以及无线传感器网络(Wireless Sensor Networks, WSNs) [1-3]等的飞速发展, 利用无线网络的目标定位技术已经成为环境监测、室内定位、无线电监控等[4, 5]领域中众多学者关注的热点问题.
现今, 已有大量关于WSNs定位算法的研究成果. 根据传感器测量值的物理变量类型划分, 可分为3类: 基于到达角度定位 (Angle of Arrival, AoA)、基于到达时间差 (Time Difference of Arrival, TDoA) 定位和基于接收信号强度指数(Received Signal Strength Indicator, RSSI)定位[6, 7]. 其中基于RSSI的 WiFi和ZigBee等技术具有低成本、低功耗、易部署等优势, 使得基于 RSSI 的室内定位得到了广泛关注.
基于RSSI的定位方法的基本工作原理是利用 RSSI值与距离之间存在的关系, 根据终端测量接收到的信号强度和已知的无线测距模型, 估算出收发方之间的距离. 然而, 在实际应用中, 噪声的多模态和复杂多变的特性给精确定位带来巨大障碍, 使得定位性能得不到保障. 针对该问题, 主流的处理方法有两种: 一种以拓展卡尔曼滤波(Extended Kalman Filtering, EKF)方法[8, 9]为代表, 根据噪声的统计特性进行分析; 另一种以集员滤波(Set-Membership Filtering, SMF) 方法[10, 11]为代表, 将噪声看作是幅值有界但大小未知的量进行分析. 然而, 在实际的应用中, 精确的噪声统计特性是无法获取的, 这大大降低了EKF的性能. 而这些杂乱噪声信号虽是未知的, 但是噪声的边界容易获得, 因而本文考虑采用集员滤波方法来处理未知但有界的噪声.
文献[10]提出集员滤波后, 集员滤波在理论与应用上都引起了很多学者的关注. 文献[11]采用集员滤波对带有非线性有约束的系统进行了分析, 考虑了非线性函数线性化时基点误差和截断误差对状态估计的影响. 文献[12]解决了一类具有传感器饱和的离散时变系统的集员滤波问题. 然而这些研究成果仅适用于单目标系统. 近年来, 随着传感器成本的逐年下降以及高精度、多目标定位的需求越来越多, 很多学者开始倾向于研究针对多目标的分布式多边椭圆定位, 以提升定位精度并准确刻画目标状态. Le Thu Nguyen等[13]提出了基于序列蒙特卡罗方法的多源定位系统. Meng等[14]针对WSN 中基于能量的多源定位, 提出了一种有效的EM算法. 在此基础上, Meng等[15, 16]基于集员滤波思想, 分析了声能损耗模型下的多源椭圆定位问题. 然而, 由于声能模型的结构特性, 使得其分析难度过大, 且当锚节点与待测节点距离过近时高阶余项无界, 无法满足定位要求.
本文针对基于RSSI的多目标定位问题, 提出点估计与椭圆估计相融合的分布式多边融合定位算法. 首先, 通过多边定位算法进行粗定位. 其次通过集员滤波方法求解多目标椭圆定位问题. 值得指出的是, 与以往的优化算法不同, 本文提出的优化算法获得的结果为可以包含真实目标节点位置的椭圆集, 而非一个最优估计点.
2 问题描述 2.1 系统组成本文研究了无线传感网络上基于 RSSI的室内多目标的定位问题. 传感网络结构如图1所示.

|
图 1 传感网络结构 |
图1中, N个待测节点通过通信信道向附近的锚节点发送信号, 分布在已知位置的N个锚节点分别接收RSSI并传输到数据处理中心. 数据处理中心首先通过多边定位算法进行粗定位, 然后再通过集员滤波进一步优化定位性能.
2.2 RSSI测距模型在利用RSSI定位时, 一般采用对数分布阴影模型[17]来确定距离与测量值间的关系, 其形式如下:
| ${\textit{RSSI}} = \alpha - {\rm{10}}\gamma \times {\rm{ lg}}(d{\rm{/}}{d_{\rm{0}}})$ | (1) |
式中,
| $d = {d_0} \times {10^{\frac{{\alpha - {\textit{RSSI}}}}{{10\gamma }}}}$ | (2) |
本文假定参数
数据处理中心接收到各锚节点的RSSI信号后, 即可利用RSSI测距模型得出测量距离, 然后通过多边定位算法对待测节点位置进行估计. 方法如下:
设分布在已知空间中特定位置的L个锚节点的坐标集为
| $\left\{ {\begin{array}{*{20}{c}} {{{{\rm{(}}{{{A}}_1} - {{{{\hat a}}}_n})}^2} + {{{\rm{(}}{{{B}}_1} - {{{{\hat b}}}_n})}^2} = d_{1, n}^2} \\ {{{{\rm{(}}{{{A}}_2} - {{{{\hat a}}}_n})}^2} + {{{\rm{(}}{{{B}}_2} - {{{{\hat b}}}_n})}^2} = d_{2, n}^2} \\ \vdots \\ {{{{\rm{(}}{{{A}}_L} - {{{{\hat a}}}_n})}^2} + {{{\rm{(}}{{{B}}_L} - {{{{\hat b}}}_n})}^2} = d_{L, n}^2} \end{array}} \right.$ | (3) |
式(3)可以转化为:
| $\left\{ {\begin{array}{*{20}{c}} { - {\rm{2}}{{{A}}_1}{{{{\hat a}}}_n} - 2{{{B}}_1}{{{{\hat b}}}_n} + {{\hat a}}_n^2 + {{\hat b}}_n^2 = d_{1, n}^2 - {{A}}_1^2 - {{B}}_1^2} \\ { - {\rm{2}}{{{A}}_2}{{{{\hat a}}}_n} - 2{{{B}}_2}{{{{\hat b}}}_n} + {{\hat a}}_n^2 + {{\hat b}}_n^2 = d_{2, n}^2 - {{A}}_2^2 - {{B}}_2^2} \\ \vdots \\ { - {\rm{2}}{{{A}}_L}{{{{\hat a}}}_n} - 2{{{B}}_L}{{{{\hat b}}}_n} + {{\hat a}}_n^2 + {{\hat b}}_n^2 = d_{L, n}^2 - {{A}}_L^2 - {{B}}_L^2} \end{array}} \right.$ | (4) |
式(4)可以表示为:
| ${{H}}{{\hat{ x}}_n} = {{{G}}_n}$ | (5) |
式中,
| ${{{G}}_n} = \left( {\begin{array}{*{20}{c}} {d_{1, n}^2 - {{A}}_1^2 - {{B}}_1^2 - d_{L, n}^2 + {{A}}_L^2 + {{B}}_L^2} \\ {d_{2, n}^2 - {{A}}_2^2 - {{B}}_2^2 - d_{L, n}^2 + {{A}}_L^2 + {{B}}_L^2} \\ \vdots \\ {d_{L - 1, n}^2 - {{A}}_{L - 1}^2 - {{B}}_{L - 1}^2 - d_{L, n}^2 + {{A}}_L^2 + {{B}}_L^2} \end{array}} \right)$ | (6) |
| ${\boldsymbol{H}} = - 2 \times \left( {\begin{array}{*{20}{c}} {{{{A}}_1} - {{{A}}_L}} \\ {{{{A}}_2} - {{{A}}_L}} \\ \vdots \\ {{{{A}}_{L - 1}} - {{{A}}_L}} \end{array}\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array}\begin{array}{*{20}{c}} {{{{B}}_1} - {{{B}}_L}} \\ {{{{B}}_2} - {{{B}}_L}} \\ \vdots \\ {{{{B}}_{L - 1}} - {{{B}}_L}} \end{array}} \right)$ | (7) |
解方程(7)可得第n个待测节点坐标为:
| ${{\hat{x}}_n} = {({{{H}}^{\rm{T}}}{{H}})^{ - 1}}{{{H}}^{\rm{T}}}{{{G}}_n}$ | (8) |
同理, 可以获得其它所有待测节点的坐标, 即可以求出坐标集
| ${{\beta}}_n^0 = \{ {{x}} \in {{{R}}^2}:{({{{x}}_n} - {{\hat{x}}^0}_n)^{\rm{T}}}{({{P}}_n^0)^{ - 1}}({{{x}}_n} - {\hat{x}}_n^0) \le 1\} $ | (9) |
式中,
包含真实状态集x的有界集
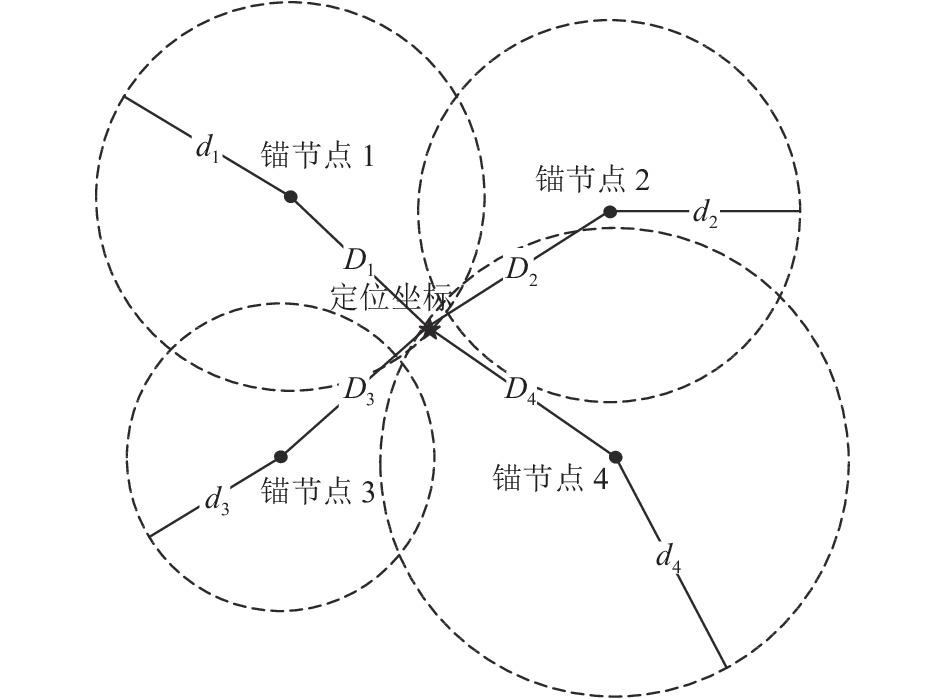
|
图 2 多边定位示意图 |
3 集员滤波 3.1 优化模型构建
获得包含真实目标位置的初始椭圆后, 重新对定位模型进行分析, 每个传感器的测量值可重新表示为:
| ${y_l} = \sum\limits_{n = 1}^N {\left(\alpha - {\rm{10}}\gamma \times {\rm{lg}}\left(\frac{{{\rm{||}}{{{x}}_n} - {{{r}}_l}{\rm{||}}}}{{{d_{\rm{0}}}}}\right)\right)} + {\lambda _l}{v _l}$ | (10) |
式中,
此外, 将l个传感器的所有测量值记为
| $f({{x}}) = \sum\limits_{n = 1}^N {{f_n}} ({{{x}}_n})$ | (11) |
其中,
| ${{y}} = f({{x}}) + {v}$ | (12) |
式中,
利用泰勒公式, 将函数
| $f({{x}}) = f({\hat{x}}) + J({\hat{ x}})({{x}} - {\hat{x}}) + \nabla f({{x}}, {\hat{x}})$ | (13) |
式中,
| $\nabla f({{x}}, {\hat{x}}) \in {{\zeta }} = \left\{ {\textit{z}} \in {{{R}}^L}:{{D}}_l^f \le {{\textit{z}}_l} \le {{U}}_l^f\right\} $ | (14) |
其中,
结合式(11)和式(13)可得, 在第i次优化时:
| $\nabla f({{x}}, {{\hat{x}}^i}) = \sum\limits_{n = 1}^N {({f_n}({{{x}}_n}) - {f_n}({{{\hat{x}}}^i}_n) - {J_n}({{{\hat{x}}}^i}_n)({{{x}}_n} - {{{\hat{x}}}^i}_n))} $ | (15) |
式中,
| $\nabla {f_n}({{{x}}_n}, {\hat{x}}_n^i) = {f_n}({{{x}}_n}) - {f_n}({{\hat{x}}^i}_n) - {J_n}({{\hat{x}}^i}_n)({{x}_n} - {{\hat{x}}^i}_n)$ | (16) |
式中,
对于任意
| $\nabla {f_n}({{{x}}_n}, {\hat{x}}_n^i) \in {{\zeta }}_n^i = \left\{ {\textit{z}} \in {{{R}}^N}:{{D}}_{l, n}^{f, i} \le {{\textit{z}}_l} \le {{U}}_{l, n}^{f, i}\right\} $ | (17) |
式中,
式(14)中有界余项
| ${{{D}}^{f, i}} = \sum\limits_{n = 1}^N {{{D}}_n^{f, i}} ,\;{{{U}}^{f, i}} = \sum\limits_{n = 1}^N {{{U}}_n^{f, i}} $ | (18) |
由文献[16]的命题1可知, 在求解有界集
定理1. 如果目标节点位置总包含于一个有界集
| $\begin{split}U_{l, n}^{f, i}&=\mathop{\max}\limits_{{{{x}}_n}\in {\beta}_n^i} \nabla {f_{l, n}}({{{x}}_n}, {\hat{x}}_n^i)\\ & = \max \left\{ {\nabla {{\tilde f}_{l, n}}\left( { - 1, R_n^i} \right), \nabla {{\tilde f}_{l, n}}\left( {1, R_n^i} \right), 0} \right\} \end{split}$ | (19) |
| $ D_{l, n}^{f, i}=\mathop {\min }\limits_{{{{x}}_n} \in {\beta}_n^i} \nabla {f_{l, n}}({{{x}}_n}, {\hat{x}}_n^i) = \min \left\{ {\nabla {{\tilde f}_{l, n}}\left( {{k_1}, R_n^i} \right), 0} \right\} $ | (20) |
式中,
证明: 令
| $\nabla {{\tilde f}_{l, n}}(\Delta {{x}}) = 10\gamma \times (\dfrac{{{{({\hat{x}}_n^i - {{{r}}_l})}^{\rm{T}}}}}{{{\rm{||}}{\hat{x}}_n^i - {{{r}}_l}{\rm{|}}{{\rm{|}}^{\rm{2}}}{\rm{ln10}}}}\Delta {{x}}{ + \lg \dfrac{{||{\hat{x}}_n^i - {{{r}}_l}||}}{{||{\hat{x}}_n^i - {{{r}}_l} + \Delta {{x}}||}})} $ | (21) |
记
| $ \nabla {\tilde f_{l, n}}(k, t) = 10\gamma [\frac{{kt}}{{{\tau _l}\ln 10}} + \lg {\tau _l} - \frac{1}{2}\lg ({t^2} + {\tau ^2} + 2t{\tau _l}k)] $ | (22) |
式中,
余下证明可分为两部分: (1)求当
(1)首先, 观察可知, 当t=0时, 函数
① 当k=–1时,
② 当k=1时,
综上可得:
| $\mathop{\max}\limits_{{{{x}}_n} \in {\beta}_n^i} \nabla {{\tilde f}_{l, n}}({{{x}}_n}, {\hat{x}}_n^i) = \max \left\{ {\nabla {{\tilde f}_{l, n}}\left( { - 1, R_n^i} \right), \nabla {{\tilde f}_{l, n}}\left( {1, R_n^i} \right)0} \right\} $ | (23) |
(2)同理, 可得:
| $\mathop{\min}\limits_{{{{x}}_n} \in {\beta}_n^i} \nabla {{\tilde f}_{l, n}}({{{x}}_n}, {\hat{x}}_n^i) = \min \left\{ {\nabla {{\tilde f}_{l, n}}\left( {{k_1}, R_n^i} \right), 0} \right\} $ | (24) |
式中,
基于上述准备工作, 本节给出集员优化方法对估计的有界椭圆集进行优化.
定理2. 在第
| $\min {{Tr}}({{P}}_n^{i + 1}),\;\;{\rm{s.t.}}\;{{P}}_n^{i + 1}{\rm{ > }}{{0}}, \tau _n^x > 0, \tau _\nu ^{} > 0, {\tau _l} > 0$ | (25) |
| $\left[ {\begin{array}{*{20}{c}} { - {{P}}_n^{i + 1}}&{{{\varPhi }}_n^{i + 1}{{({{\varPsi }}_{}^{i + 1})}_ \bot }} \\ {{{({{\varPhi }}_n^{i + 1}{{({{\varPsi }}_{}^{i + 1})}_ \bot })}^{\rm{T}}}}&{ - ({{\varPsi }}_{}^{i + 1})_ \bot ^{\rm{T}}{{\varXi }}_n^{i + 1}{{({{\varPsi }}_{}^{i + 1})}_ \bot }} \end{array}} \right] \le 0$ | (26) |
式中,
| ${{\varPhi }}_n^{i + 1} = [{{x}}_n^i - {\hat{x}}_n^{i + 1}, {{E}}_n^i, {\boldsymbol{0}}, {\boldsymbol{0}}]$ | (27) |
| ${{\varPsi }}_{}^{i + 1} = [f({{\hat{ x}}^i}) + {{\hat{e}}^i} - {{y}}, {{{J}}^i}{{{E}}^i}, {\rm{diag}}({{\hat{b}}^i}), {{\lambda }}]$ | (28) |
| ${{{\varXi }}_n} = {\rm{diag}}(1 - \tau _n^x - \sum\limits_{l = 1}^L {{\tau _m}} - \tau _v ^{}, \tau _n^xI, {\rm{diag}}({\tau _1}, \cdots , {\tau _L}), \tau _v ^{}{Q^{ - 1}})$ | (29) |
证明: 由式
| ${{{x}}_n} - {\hat{x}}_n^{i + 1} = {\hat{x}}_n^i + {{E}}_n^i{{\mu }} - {\hat{x}}_n^{i + 1}$ | (30) |
另外, 结合式(12)和式(13)可得:
| ${{y}} = f({{x}}) + v= f({\hat{x}}) + {{{J}}^i}{{{E}}^i}{{\mu }} + {{{\hat{e}}}^i} + {\rm{diag}}({{{\hat{b}}}^i}){{\varDelta }} + {{\lambda v}} $ | (31) |
记
| ${{{x}}_n} - {\hat{x}}_n^{i + 1} = {{\varPhi }}_n^{i + 1}{{\xi }}$ | (32) |
| ${{\varPsi }}_{}^{i + 1}{{\xi }} = {{0}}$ | (33) |
那么, 由
| ${({{\varPhi }}_n^{i + 1}{{\xi }})^{\rm{T}}}{({{P}}_n^{i + 1})^{ - 1}}{{\varPhi }}_n^{i + 1}{{\xi }} \le 1$ | (34) |
其满足,
| ${{{\xi }}^{\rm{T}}}{({{\varPsi }}_{}^{i + 1})^{\rm{T}}}{{\varPsi }}_{}^{i + 1}{{\xi }} = 0$ | (35) |
| ${{{\xi }}^{\rm{T}}}{\rm{diag}}\left( { - 1, {{I}}, {\boldsymbol{0}}, {\boldsymbol{0}}} \right){{\xi }} \le 0$ | (36) |
| ${{{\xi }}^{\rm{T}}}{\rm{diag}}( - 1, {\boldsymbol{0}}, \cdots \overbrace {0, \cdots , 1, \cdots , 0}^{{\text{第}}l{\text{个元素为}}1} \cdots , {\boldsymbol{0}}){{\xi }} \le 0$ | (37) |
| ${{{\xi }}^{\rm{T}}}{\rm{diag}}( - 1, {\boldsymbol{0}}, {\boldsymbol{0}}, {{Q}}_{}^{ - 1}){{\xi }} = 0$ | (38) |
由S-procedure 引理[18, 19]可得, 存在正定参数
| $\begin{split} & {({{\varPhi }}_n^{i + 1})^{\rm{T}}}{({{P}}_n^{i + 1})^{ - 1}}{{\varPhi }}_n^{i + 1} - {\rm{diag}}(1, {\boldsymbol{0}}, {\boldsymbol{0}}, {\boldsymbol{0}}) \\ & - \sum\limits_{l = 1}^L {{\tau _l}} {\rm{diag}}( - 1, {\boldsymbol{0}}, \cdots \overbrace {0, \cdots , 1, \cdots , 0}^{{\text{第}}l{\text{个元素为}}1} \cdots , {\boldsymbol{0}}) \\ & - \tau _n^x{\rm{diag}}( - 1, I, {\boldsymbol{0}}, {\boldsymbol{0}}) - \tau _\nu ^{}{\rm{diag}}( - 1, {\boldsymbol{0}}, {\boldsymbol{0}}, {{Q}}_{}^{ - 1}) \\ & - {\tau _y}{({{\varPsi }}_n^{i + 1})^{\rm{T}}}{{\varPsi }}_n^{i + 1} \le 0 \end{split} $ | (39) |
根据Schur-Complements引理[18], 式(39)可转化为式(26). 证毕.
利用定理2中式(25), 式(26)对椭圆集进行优化时, 为了降低计算的复杂度, 可设置一个阈值
为验证本文所提算法的有效性和实用性, 选取面积为10 m×10 m的空地进行实验, 实验的场景如图3所示. 实验中采用带有CC2530芯片的无线模块接收和发送信号, 以1 m为单位长度, 9个锚节点规则的排布在方形区域中, 其坐标分别为(0.5, 0.5), (0.5, 5), (0.5, 9.5), (5, 0.5), (5, 5), (5, 9.5), (9.5, 0.5), (9.5, 5), (9.5, 9.5), 3个待测节点坐标分别为(2.5, 7), (5, 2.5), (6, 7).

|
图 3 实验场景 |
通过实验获取RSSI数据后, 在带有YALMIP和SeDuMi工具箱的Matlab R2016a仿真平台对数据进行处理. 仿真中初始参数设置如表1所示.
| 表 1 参数设置 |
简单处理实验数据, 得到RSSI的平均值, 然后通过2.2节和2.3节的定位算法计算出初值, 再利用第3节中集员滤波优化算法对初始估计区域进行优化, 仿真运行结果如图4所示.

|
图 4 DMFL算法的定位示意图 |
图4展示本文所提算法优化过程中和最终优化的各目标所处的椭圆区域, 定位 所得椭圆的中心点分别为(2.3621, 7.0539), (4.9891, 2.7220), (6.0852, 6.9940), 用椭球中心点与待测节点之间的距离差表示估计误差, 这种情况下所得的估计误差分别为 0.0995 m、0.2747 m和0.1052 m. 另外从图4可以看出, 采用该算法定位获得的椭圆集总能包含真实的待测节点坐标, 体现了良好的定位性能.
为了证明DMFL算法的优越性, 与文献[20]中的多边定位算法(Multi-lateral Localization Algorithm, MLA)算法和文献[12]中的分布式集员滤波(Distributed Set-Membership Filtering, DSMF)算法进行了对比. 定位误差比较结果如表2所示.
| 表 2 3种算法的误差比较(m) |
3种算法的运行时间分别为0.017 s, 1.864 s和2.427 s.
从表2中的均值栏可以看出, 相比于DSMF和MLA算法, 本文所提的DMFL算法定位的误差最小. 此外, DMFL算法对各待测节点的定位误差最大不超过0.3 m, 体现出该算法具有较好的鲁棒性能. 从运行的时间成本来看, DMFL算法与DSMF算法运行时间相近, 均远大于MLA算法的运行时间, 这也是这两种算法为实现高精度定位时所不可避免的.
另外, 为了探究锚节点个数、迭代次数与估计误差的关系, 图5(a)中展示了优化迭代4次时锚节点个数与估计误差的关系, 图5(b)中展示了有9 个锚节点时迭代次数与估计误差的函数关系.
从图5(a)和图5(b)中可以看出估计误差随着锚节点数量的增多和迭代次数的增加而减小, 最终趋于平稳. 然而, 锚节点数量的增多和迭代次数的增加意味着定位成本和时间消耗的增加. 因此在实际应用中需要根据需要权衡锚节点的布置数量和优化算法的迭代次数. 从图5(a)中可以看出迭代4次时布置7个锚节点是较优的选择, 从图5(b)中可以得出布置9个锚节点时迭代2次是较优的选择.
当对多个目标进行定位时, 由于受折射、衍射等的影响, 定位性能与待定位目标定个数也存在较大关系. 一般待定位目标越多, 信号受折射、衍射的影响越大, 即获取的信号的噪声越大. 为验证噪声未知但有界条件下, 噪声大小对定位性能的影响, 通过电脑模拟测量值进行了200次蒙特卡罗仿真验证, 仿真中锚节点和待测节点布置方式相同, 迭代次数为4次, 仿真结果如图6. 此外, 通过图7展示了锚节点不规则排布时仍能实现有效定位.

|
图 5 DMFL锚节点数、迭代次数与估计误差的关系 |

|
图 6 DMFL噪声大小与估计误差的关系图 |
5 总结
本文针对多目标定位精度低、性能差的问题进行了详细分析, 并提出了相应的优化方法. 首先, 采用多边定位算法进行粗定位, 获取初值. 其次, 通过在线分析获取了泰勒展式的高阶有界余项. 然后, 利用迭代优化算法求解了多目标椭圆定位问题. 最后, 通过实验和仿真证明了所提定位算法的可行性与有效性. 结果表明:
(1)本文所提出的算法定位精度高于DSMF和MLA算法, 且性能更为稳定, 定位误差最大不超过0.3 m, 更适用于实际环境.

|
图 7 随机布置锚节点时DMFL算法的定位示意图 |
(2)锚节点个数、迭代次数、噪声大小对估计误差均有较大影响. 但随着锚节点个数和迭代次数的增加, 估计误差缩小的幅度在降低.
(3)在锚节点规则分布和随机分布情况下, 该算法均可实现可靠定位, 给出包含目标位置的最优椭圆区域.
| [1] |
Laoudias C, Moreira A, Kim S, et al. A survey of enabling technologies for network localization, tracking, and navigation. IEEE Communications Surveys & Tutorials, 2018, 20(4): 3607-3644. |
| [2] |
Elhabyan R, Shi W, St-Hilaire M. Coverage protocols for wireless sensor networks: Review and future directions. Journal of Communications and Networks, 2019, 21(1): 45-60. DOI:10.1109/JCN.2019.000005 |
| [3] |
游康勇, 杨立山, 郭文彬. 无线传感器网络下基于压缩感知的多目标分层贪婪匹配定位. 自动化学报, 2019, 45(3): 480-489. |
| [4] |
Behera TM, Mohapatra SK, Samal UC, et al. I-SEP: An improved routing protocol for heterogeneous WSN for IoT-based environmental monitoring. IEEE Internet of Things Journal, 2020, 7(1): 710-717. DOI:10.1109/JIOT.2019.2940988 |
| [5] |
吴鹏, 于世东. 基于UWB室内送餐机器人定位信息系统. 计算机系统应用, 2021, 30(1): 101-105. DOI:10.15888/j.cnki.csa.007767 |
| [6] |
Zafari F, Gkelias A, Leung KK. A survey of indoor localization systems and technologies. IEEE Communications Surveys & Tutorials, 2019, 21(3): 2568-2599. |
| [7] |
曹建荣, 张旭, 武欣莹, 等. 结合CNN和WiFi指纹库的室内定位算法. 计算机系统应用, 2020, 29(7): 173-179. DOI:10.15888/j.cnki.csa.007492 |
| [8] |
Kalman RE. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 1960, 82(1): 35-45. DOI:10.1115/1.3662552 |
| [9] |
Calafiore G. Reliable localization using set-valued nonlinear filters. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2005, 35(2): 189-197. DOI:10.1109/TSMCA.2005.843383 |
| [10] |
Schweppe FC. Recursive state estimation: Unknown but bounded errors and system inputs. IEEE Transactions on Automatic Control, 1968, 13(1): 22-28. DOI:10.1109/TAC.1968.1098790 |
| [11] |
Yang FW, Li YM. Set-membership filtering for systems with sensor saturation. Automatica, 2009, 45(8): 1896-1902. DOI:10.1016/j.automatica.2009.04.011 |
| [12] |
Yang B, Qiu QW, Han QL, et al. Received signal strength indicator-based indoor localization using distributed set-membership filtering. IEEE Transactions on Cybernetics, 2020.
|
| [13] |
Le Thu Nguyen T, Septier F, Rajaona H, et al. A bayesian perspective on multiple source localization in wireless sensor networks. IEEE Transactions on Signal Processing, 2016, 64(7): 1684-1699. DOI:10.1109/TSP.2015.2505689 |
| [14] |
Meng W, Xiao WD, Xie LH. An efficient EM algorithm for energy-based multisource localization in wireless sensor networks. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 1017-1027. DOI:10.1109/TIM.2010.2047035 |
| [15] |
Meng FQ, Shen XJ, Wang ZG, et al. Set-membership multiple-source localization using acoustic energy measurements. 2017 20th International Conference on Information Fusion (Fusion). Xi’an: IEEE, 2017. 1–7.
|
| [16] |
Meng FQ, Shen XJ, Wang ZG, et al. Multiple-source ellipsoidal localization using acoustic energy measurements. Automatica, 2020, 112: 108737. DOI:10.1016/j.automatica.2019.108737 |
| [17] |
Braun WR, Dersch U. A physical mobile radio channel model. IEEE Transactions on Vehicular Technology, 1991, 40(2): 472-482. DOI:10.1109/25.289429 |
| [18] |
Boyd SP, El Ghaoui L, Feron E, et al. Linear matrix inequalities in system and control theory. Philadelphia: Society for Industrial and Applied Mathematics, 1994.
|
| [19] |
Skelton RE, Iwasaki T, Grigoriadis KM. A Unified Algebraic Approach to Linear Control Design. Bristol: Taylor & Francis, 1998.
|
| [20] |
Shu T, Chen YY, Yang J. Protecting multi-lateral localization privacy in pervasive environments. IEEE/ACM Transactions on Networking, 2015, 23(5): 1688-1701. DOI:10.1109/TNET.2015.2478881 |
 2021, Vol. 30
2021, Vol. 30



