电力对现代社会活动至关重要, 为了保证电力设备的正常运转, 需要对电力线路进行有效的监测和维护, 在电力设施不足的情况下甚至需要带电作业. 我国现阶段输电线路巡检方法包括作业人员实地巡检和低空巡检^[1-3]. 实地勘察由于实际作业中配电线路结构复杂、作业项目难度高、作业组织流程多等因素, 存在着安全距离不足或触碰带点或接地体接触等问题, 导致安全风险较高或发生触电事故; 低空巡检方法则主要采用直升机进行肉眼巡查或手持仪器进行数据采集, 劳动强度大, 工作效率低, 难以适应现代化电力网络建设与维护的发展^[4]. 带电作业是提高供电可靠性的有效手段之一, 但在实际作业中由于配电线路结构的复杂性、作业项目的难度、作业组织流程多、现场安全管控能力不足、操作人员的技术技能水平及安全意识等综合因素影响, 在作业过程会出现带电作业的安全距离不足或触碰带电体或与接地体接触, 导致安全风险较高或发生触电事故.

传感器技术的发展使得非接触式巡检的成本降低, 基于可见光航拍的电力巡检是目前的一种常用手段, 通过摄像机采集照片、视频等图像数据进行事后数据处理, 机器视觉技术的快速发展使得故障诊断的自动化程度和精度取得巨大的提高^[5]. 激光雷达测量技术是一种日渐成熟的高精度测量技术, 可以获取目标地物的高精度空间位置信息, 与基于图像的提取电力线检测方式相比, 基于激光雷达点云数据的识别方法可以避免二维(2D)光栅图像不可避免的一些问题, 如光照变化和背景混淆^[6-8]. 基于以上现状分析, 本文设计并实现了一套基于非接触远距离高精度的激光雷达配电线路安全距离监测预警系统, 用以安全距离测量、作业安全监测以及可视化监控, 实现作业现场的实时管控, 为作业人员的安全防护提供保障, 避免安全隐患, 提高带电作业的安全水平.

1 安全距离监测预警系统方案

为了实现10 kV配电线路带电作业周边环境安全距离测量与预警, 在电力作业斗臂车四周安装4套单线激光雷达(思岚RPLIDAR S1)与大疆GM6020云台电机的组合设备进行三维电力带电作业环境感知, 这样的组合具备体积小、质量轻的特点. 通过网络实时的将4套设备实时采集的点云数据传输至数据处理平台进行可视化显示、安全距离监测与预警. 安全距离监测预警系统整体方案如图1所示.

思岚RPLIDAR S1是一款TOF激光雷达, 小巧轻便, 单个重量仅105 g, 采样频率10 Hz, 最大测量距离可达40 m, 典型角度分辨率为0.391°, 可以有效避免环境光与强日光的干扰, 实现室外场景的稳定测距. RoboMaster GM6020是一款内部集成驱动器的高性能直流无刷电机, 电机重量仅约468 g, 电机采用空心轴设计, 扭矩密度大、控制精度高、交互方式灵活、保护功能强. 点云采集通过集成的微型计算机(使用树莓派操作系统)进行控制, 集成的点云采集设备如图2所示.

2 多激光雷达标定

低成本激光雷达通常面临点云稀疏无法提取有效信息的问题, 将多个激光雷达组合起来, 能够增加激光雷达的有效测量范围^[9]. 单个激光雷达输出的原始数据为扫描点在该激光雷达自身坐标系下的三维坐标及反射率, 由于思岚RPLIDAR S1单线雷达和RoboMaster GM6020电机的组合设备安装在斗臂车的侧面, 相互之间并不通视, 单套设备只能感知到一个方向上的环境信息, 因此需要融合4套设备点云数据以获取电力作业斗臂车全方位的环境信息. 4套设备之间需要标定空间位置关系以进行多激光雷达点云融合, 实际应用中应将点云归算到以斗臂车中心点为原点的坐标系下.

为了达到目的, 我们需要精确的校准传感器之间的六自由度刚体变换, 根据是否设置人工目标, 标定方法大致被分为两种. 近年来, 有学者提出了一种利用场景反射强度提取点强度的方法实现多激光雷达的标定算法, 根据点云的几何特征, 使得能够离线的标定任意场景中多个二维激光雷达^[10]. 基于人工地标的方法目前被普遍用于寻找传感器之间的对应关系. Xie等提出了一种通用的标定解决方案, 在预先构建的环境中使用标签(apriltags)并联合了多个摄像头与激光雷达^[11]. Röwekämper提出了一种跟踪的方法, 利用重叠区域的运动目标对多个2D激光雷达进行标定^[12]. 程宇航等分析了5种点云拼接的精度, 包括标靶拼接、已知后视点拼接、后方交会拼接、点云试图拼接、特征点拼接, 结果表明在50 m测量距离范围内, 基于标靶的点云拼接方法精度最高^[13]. 考虑到本文的设备在实际应用中4个激光雷达之间互相不共视, 没有重叠点云, 采用标靶标定的方式更适合于本文. 本文采用了一种基于标靶纸(黑白格子)的三维激光雷达标定方法, 我们在封闭的室内空间布设多组标靶, 并利用高精度静态三维激光扫描仪确定标靶位置, 将所有的激光点云标定到统一的坐标系下.

多激光雷达空间位置关系标定就是求解各个激光雷达坐标系相对于所选定的世界坐标系的旋转参数 $\left( {Roll,Pitch,Yaw} \right)$ 和平移参数 $\left( {\Delta x,\Delta y,\Delta {\textit{z}}} \right)$ . 针对三维激光雷达外参标定求解问题, 传统方法一般根据约束关系直接对所有标定参数进行最优估计, 为了保证标定精度, 通常采用特制的标志物, 以建立严格的约束方程, 利用约束关系同时求解6个参数.

本文在室内进行模拟实验来对4套激光雷达设备进行标定, 标定场景如图3所示. 在室内平整墙面上贴黑白格子标靶纸作为参照物, 在场地中央假设架设法如(Focus 3D)高精度三维激光扫描仪, 假设其为斗臂车中心点, 在其四周摆放4套激光雷达设备进行数据采集.

法如高精度三维激光扫描仪和单线激光雷达采集的三维点云如图4所示, 在点云中可以快速便捷地提取出标靶纸的中心位置.

使用开源软件CloudCompare提取标靶纸中心点的坐标, 记场景中所有标靶纸的中心坐标在单线激光雷达坐标系 ${L_1}$ 下的坐标为 ${\{ ({x_1},{y_1},{{\textit{z}}_1}),({x_2},{y_2},{{\textit{z}}_2}), \cdots \} _{{L_1}}}$ , 在世界坐标系 $W$ 即法如坐标系下的坐标系为 $\{ ({x_1},{y_1},{{\textit{z}}_1}), $ $ ({x_2},{y_2},{{\textit{z}}_2}), \cdots \} _W$ . 世界坐标系与单线激光雷达坐标系 ${L_1}$ 之间的平移参数表示为向量 $T_{{L_1}}^W = {(\Delta x,\Delta y,\Delta {\textit{z}})^{\rm{T}}}$ , $\Delta x, $ $ \Delta y,\Delta {\textit{z}}$ 分别为沿着X, Y, Z轴的平移参数, 旋转参数表示为旋转矩阵 $R_{{L_1}}^W(\alpha ,\beta ,\gamma )$ , $\alpha ,\beta ,\gamma $ 分别为绕X, Y, Z轴旋转的旋转角度参数, 那么两套坐标系有如下转换关系:

${\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right]_W} = R_{{L_1}}^W(\alpha )R_{{L_1}}^W(\alpha )R_{{L_1}}^W(\gamma ){\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right]_{L_1}} + T_{{L_1}}^W(\Delta x,\Delta y,\Delta {\textit{z}})$

(1)

其中,

$\left\{ \begin{split}& {R}_{L1}^{W}(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{cos}\alpha & \mathrm{sin}\alpha \\ 0& -\mathrm{sin}\alpha & \mathrm{cos}\alpha \end{array}\right] \\&{R}_{L1}^{W}(\beta )=\left[\begin{array}{ccc}\mathrm{cos}\beta & 0& -\mathrm{sin}\beta \\ 0& 1& 0\\ \mathrm{sin}\beta & 0& \mathrm{cos}\beta \end{array}\right]\\& {R}_{L1}^{W}(\gamma )=\left[\begin{array}{ccc}\mathrm{cos}\gamma & \mathrm{sin}\gamma & 0\\ -\mathrm{sin}\gamma & \mathrm{cos}\gamma & 0\\ 0& 0& 1\end{array}\right]\end{split}\right.$

(2)

当旋转角度为小角度时, 可取:

$ \left\{\begin{array}{lc}\mathrm{cos}\alpha =\mathrm{cos}\beta =\mathrm{cos}\gamma =1\\ \mathrm{sin}\alpha =\alpha ,\; \mathrm{sin}\beta =\beta ,\; \mathrm{sin}\gamma =\gamma \\ \mathrm{sin}\alpha \mathrm{sin}\beta =\mathrm{sin}\alpha \mathrm{sin}\gamma =\mathrm{sin}\beta \mathrm{sin}\gamma =0\end{array}\right.$

(3)

相应的坐标转换公式变为:

${\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right]_W} = \left[ {\begin{array}{*{20}{c}} 1&\gamma &{ - \beta } \\ \gamma &1&\alpha \\ \beta &{ - \alpha }&1 \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right]_{L_1}} + \left[ {\begin{array}{*{20}{c}} {\Delta x} \\ {\Delta y} \\ {\Delta {\textit{z}}} \end{array}} \right]$

(4)

写成误差方程的形式, 可以得到:

$\begin{split}\left[ {\begin{array}{*{20}{c}} {{V_X}} \\ {{V_Y}} \\ {{V_Z}} \end{array}} \right] &= {\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right]_W} - {\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right]_{L_1}} \\&= \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{ - {Z_{L_1}}}&{{Y_{L_1}}} \\ 0&1&0&{{Z_{L_1}}}&0&{ - {X_{L_1}}} \\ 0&0&1&{ - {Y_{L_1}}}&{{X_{L_1}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta x} \\ {\Delta y} \\ {\Delta {\textit{z}}} \\ \alpha \\ \beta \\ \gamma \end{array}} \right]\end{split}$

(5)

改成矩阵的形式为: $ V=B\cdot X+\Delta $ , 其中X为待求得转换向量, V为改正数向量, $\Delta $ 为测量噪声. 按照最小二乘法 ${V^{\rm{T}}}PV = \min$ 最小得原则, 取权值为距离的倒数, 可以列出法方程为 ${B^{\rm{T}}}PBX + {B^{\rm{T}}} = 0$ , 其解为 $X = - {\left( {{B^{\rm{T}}}PB} \right)^{ - 1}} $ $ {B^{\rm{T}}}P$ . 为了求取6个转换参数, 至少需要3组公共点. Cereres solver库^[14]构建并求解上述最小二乘优化解. 通过重复上述步骤可以依次计算4个激光雷达坐标系 ${L_1}$ 与世界坐标系W的转换参数 $R_{{L_1}}^W,T_{{L_1}}^W;R_{{L_2}}^W,T_{{L_2}}^W;R_{{L_3}}^W, $ $ T_{{L_3}}^W;R_{{L_4}}^W,T_{{L_4}}^W$ , 这样可以将4个激光雷达的数据统一到同一个世界坐标系下, 实现多激光雷达点云的拼接, 标定结果如表1所示.

通过标定转换参数后, 截取4台激光雷达融合后产生的部分点云如图5所示, 可以看到点云重合度很高, 反映了标定参数的准确性, 统计同名点之间的差异, 其RMS为0.03 m, 表明标定参数可以很好的融合不同激光雷达点云.

3 软件系统开发与安全距离监测测试

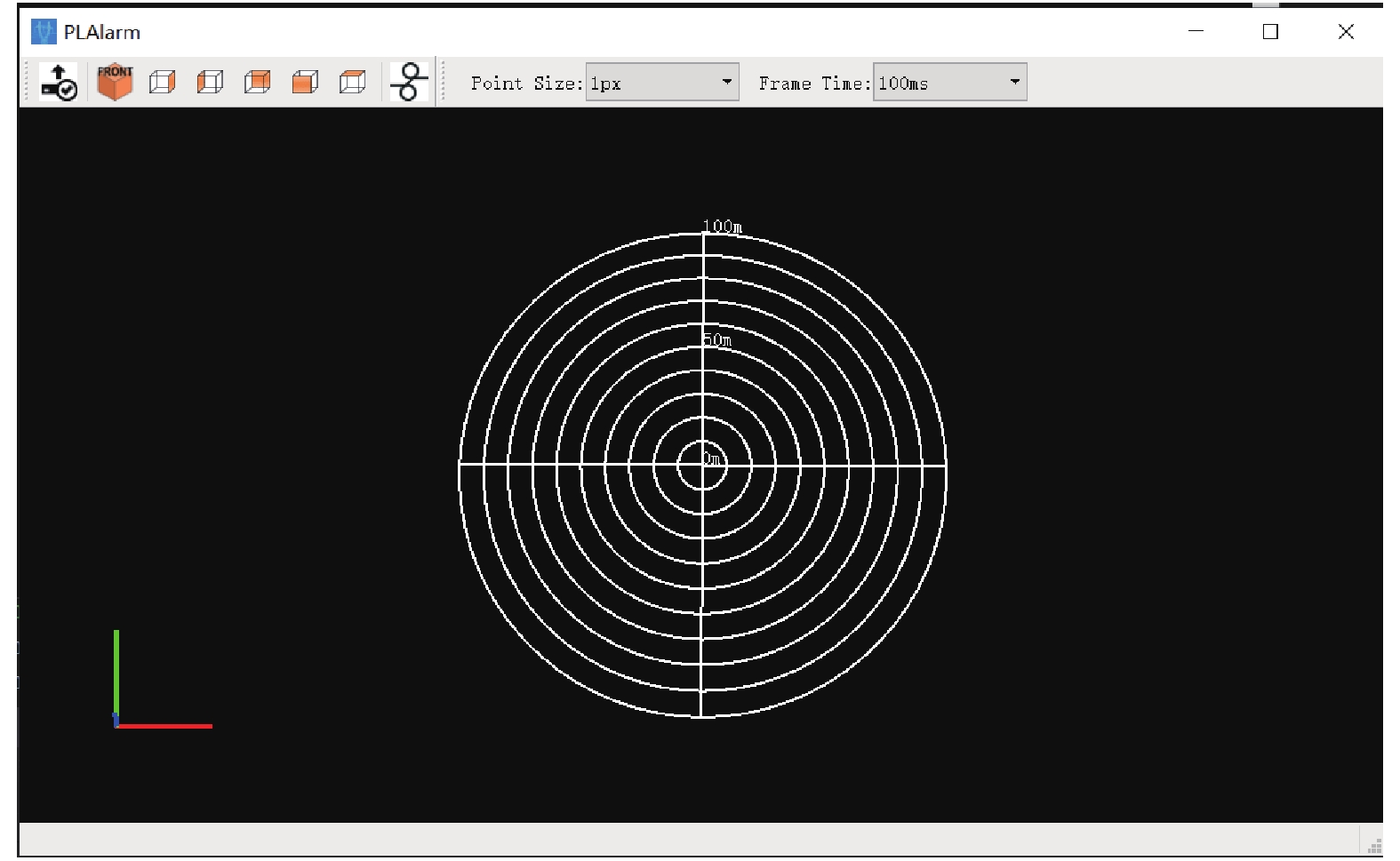
本文采用网络通信方式将4套设备采集的点云数据实时的传输至数据处理平台, 在Windows 10操作系统下基于QT平台采用C++程序设计语言开发实时采集、处理和可视化软件平台, 软件界面如图6所示. 软件功能主要包括: (1)多台激光雷达传感器实时连接及数据采集; (2)多视角点云切换(前视, 侧视, 俯视等); (3)点显示像素大小选择; (4)视场内点云积分时间, 可以选择按照100 ms, 200 ms, 500 ms, 1000 ms时间显示点云; (5)最邻近障碍物点探测, 当在设置的监测预警范围内出现障碍物时, 系统自动报警.

监测预警功能首先对每一帧点云进行降噪处理, 然后遍历当前点云帧中的每一个点并计算其与坐标原点的距离, 并找到最小距离, 如式(6)所示, 其中 ${s_i}$ 表示当前帧第i个点的距离, 如果最小距离在预警范围内, 系统会自动语音提示报警, 预警距离限值的确定是根据电力作业时的相关安全规程确定, 本文中设定预警距离为0.5 m.

$\min dist = \min \{ {s_1},{s_2},{s_3}, \cdots, {s_n}\} $

(6)

在国内某配电公司训练场10 kV电线附近进行测试, 测试场景如图7所示.

测试时, 电力维修工人在斗臂车内手持激光雷达采集设备, 如图7所示. 首先将绝缘斗臂车停于目标电线附近, 利用斗臂车绝缘斗将工作人员升到目标高度附近, 作业面与导线的距离为3 m, 这种情况下, 激光雷达能够采集的导线的最远点为4.69 m, 但导线的数据点不够, 不足以看出导线的形状, 能够采集到比导线更细但反射强度更强的斜拉钢索, 最远有效测量距离为5.59 m. 现场采集及最远距离测试结果如图8、图9所示.

然后移动斗臂车的作业斗, 使作业面与导线的距离为0.5 m的情况再次进行测量, 由于设置安全监测距离为0.5 m, 因此此时设备自动报警, 导线可测量的最远距离为4.12 m.

经过现场测试得到结论, 对于10 kV的导线, 可以保证密度足够的3 m有效测量距离. 对于金属拉线有效距离可以达到5 m以上, 也可探测到地面大型地物, 如人员, 车辆等, 能够实现电力作业安全距离监测与预警功能.

4 总结

在本文中, 提出并实现了一种基于多激光雷达的电力线安全距离监测预警系统, 通过将单线激光雷达(思岚RPLIDAR S1)与RoboMaster GM6020云台电机组合实现三维环境感知, 基于Qt平台采用C++程序设计语言开发了一套实时采集、处理和可视化软件平台, 可实现10 kV带电作业安全距离监测预警功能, 可以有效避免安全隐患, 提高带电作业的安全水平.