2. 中国科学院大学, 北京 100049;
3. 中国科学院 国家天文台, 北京 100101
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China
数值模拟是宇宙学中重要的研究方法, 它既可以帮助科学家验证理论模型和了解宇宙演化过程, 也可以与观测数据对比来完善理论模型以加深对宇宙的了解. 因此, 数值模拟为天文研究和天文观测提供了有力的数值实验方法和理论验证工具, 并已经成为现代天体物理研究中不可缺少的基本研究方法[1].
科学可视化作为一种高效的数据分析手段, 在科学模拟数据的分析中越来越重要. 科学可视化的正式提出是在20世纪80年代, 它利用图形学相关方法来帮助用户理解科学概念和了解科学数据. 传统的统计分析方法常常是分析宇宙模拟数据中各种结构的总体属性, 例如结构的质量、密度、状态和形态等, 但这种方式难以高效形象地了解和利用数值模拟数据. 科学可视化可以直观地将模拟数据中的多个物理量(例如密度、温度、压力、速度等)和特征结构展现给科学家, 同时还可以探索多个物理量之间的相互关系, 并允许科学家进行交互式分析, 这极大地提高了数据分析的效率. 此外, 针对模拟数据的时序分析, 可视化所生成的时序演化动画可以详细展示模拟中每个特征的演化过程和不同物理属性的动态变化, 这是传统的统计分析方法无法达到的.
超级计算机的发展使得计算能力快速地增长, 这同时也推动了宇宙数值模拟研究的发展. 科学家可以使用更大规模的数据进行更高精度的宇宙数值模拟, 随着模拟规模的增长, 模拟产生的数据也呈现爆炸式增长. 例如, 当前最大的宇宙学N体数值模拟所使用的数据规模达到为2万亿粒子, 模拟过程中每次数据的保存需要大约130 TB的存储空间, 通常保存单次宇宙数值模拟的数据需要PB级别的存储空间[2]. 此外, 宇宙模拟的空间跨度也越来越大. 早期模拟的焦点主要集中在宇宙大尺度结构[3], 之后银河系尺度和星系团尺度的单个暗物质晕模拟应运而生[4], 当前已经发展出从星系团到地球尺度暗物质晕的20个数量级的高精度模拟[5]. 越来越大规模的宇宙数值模拟和越来越复杂的模拟内容对科学可视化提出了新的要求也带来了新的挑战. 科学可视化不仅需要帮助科学家将模拟数据转换成图像, 同时还需要帮助和辅助专家针对不同任务进行数据分析和数据探索.
科学可视化领域发展出了多种可视化技术以应对复杂多样的可视化任务. 初期的可视化研究主要关注如何将数据展示, 即数据的绘制, 这是宇宙数值模拟数据可视化分析的基础. 近些年来, 由于数据量的剧增和数据内容的复杂多样, 通常采用多种技术与可视化相结合的方法来满足数据可视化分析的需求. 概括来说, 针对宇宙数值模拟可视化的研究以模拟数据的绘制为基础, 以模拟数据规模的增长和数据分析研究的发展为推动, 在近些年来呈现出以下几个方面的研究主题:
1) 交互可视化: 利用交互技术辅助用户对可视化内容进行交互式分析, 以实现特定任务分析为目的.
2) 并行可视化: 利用并行计算或者GPU计算加速对数据的处理并提高数据绘制效率, 以达到分析或者绘制大规模模拟数据的目的.
3) 原位可视化: 利用原位处理方法, 在模拟的计算节点上对数据进行原位处理, 解决I/O瓶颈和存储限制的问题, 以达到超大规模数据可视化与分析的目的.
4) 机器学习与可视化: 利用机器学习的相关算法对数值模拟数据进行处理和分析, 然后进行可视化分析, 以提高数据分析的能力和效率.
本文首先介绍了宇宙数值模拟的数据结构和发展趋势, 然后对当前所使用的模拟数据绘制算法进行总结. 在此基础上, 介绍了当前主要研究主题下的多个研究案例, 归纳了不同研究主题下的研究主线, 最后进行了总结和展望.
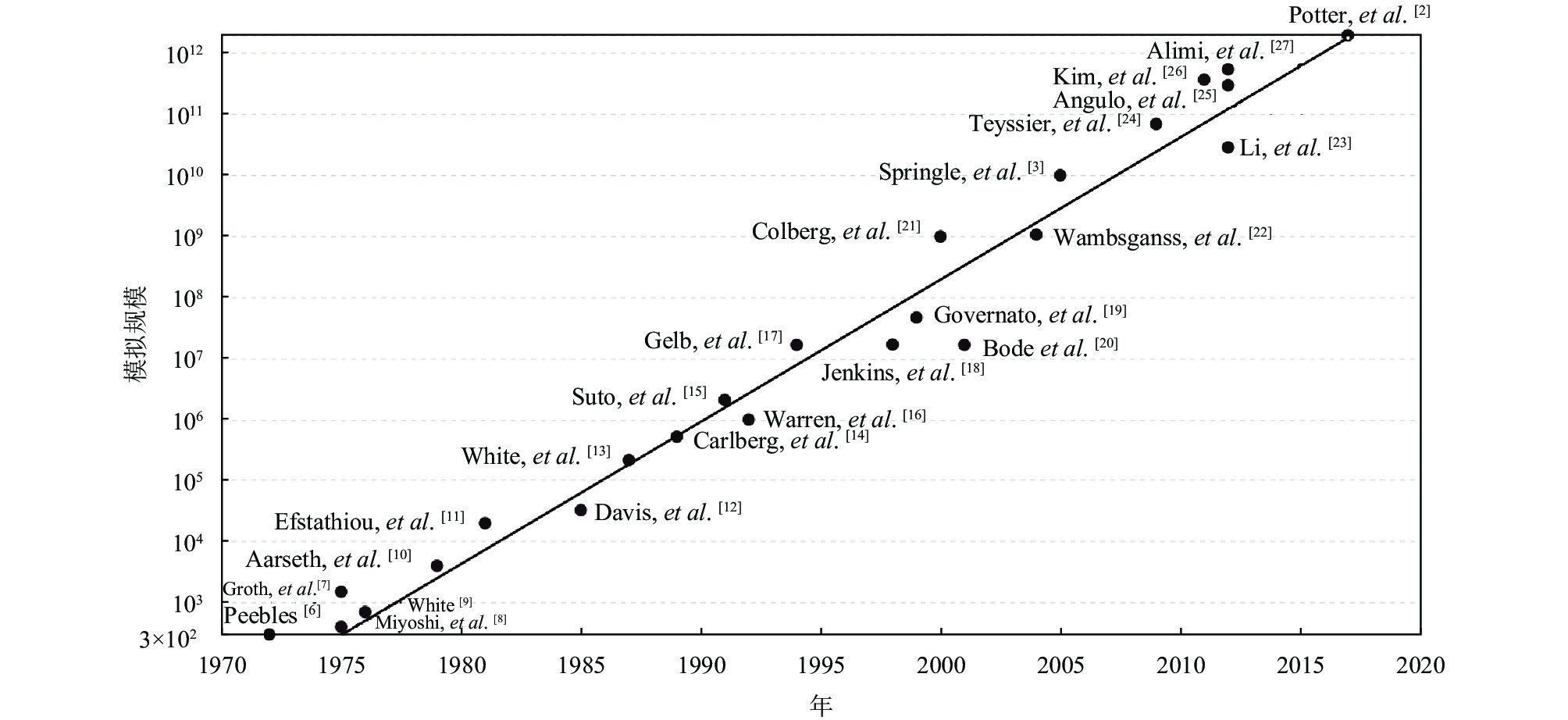
1 宇宙数值模拟程序与模拟数据宇宙数值模拟起源于20世纪70年代, 最早的宇宙数值模拟为Peebles等[6]使用了大约300个粒子的N体模拟对星系团进行研究. 随着超级计算机的发展和宇宙学研究的深入, 宇宙数值模拟的数据规模不断增长, 模拟的数据规模增加速度与“摩尔定律”大致相符, 即每间隔大约18个月数据量就增加一倍. 时间与模拟规模的增长关系如图1所示, 图中线为“摩尔定律”曲线, 从图中可以看出粒子增长速度与“摩尔定律”大致相符. 随着E级计算的到来, 宇宙数值模拟的规模将会更大, 对模拟的精度也会更高, 对宇宙的分析也会越来越精确, 同时伴随着更多的大规模巡天观测结果的出现, 宇宙模型也将更加准确. 因此, 从宇宙数值模拟的规模发展趋势上来说, 模拟所使用的数据量会继续增加, 并且模拟的精度也会越来越高.
宇宙数值模拟程序所使用的模拟数据结构可以简单分为两类, 即网格数据和离散数据. 网格数据中又分为均匀网格和非均匀网格, 网格数据是将三维模拟空间划分为网格, 每个格点记录相关的物理变量. 模拟程序在使用网格数据进行计算时, 引力的计算以网格为基本单位, 模拟所保存的模拟数据格式为网格数据. 离散数据即粒子数据, 使用大量的粒子数据来覆盖三维模拟空间, 粒子属性包含位置、速度、质量、加速度等多个物理量. 模拟程序在使用粒子数据进行模拟的过程中, 引力的计算以粒子或者网格为基本单位, 模拟所保存的模拟数据格式为粒子数据.
2 宇宙数值模拟数据的绘制
数值模拟程序所保存的数据无法直观地展示, 需要进行数据处理和绘制, 模拟数据的绘制是可视化分析的基础. 数据的绘制方法从对原始数据的操作上可以分为3类, 即直接映射绘制、光滑核处理绘制和数据重组织绘制. 本章节将介绍每种绘制算法的基本原理, 并且给出在同一数据集下每种算法的可视化展示图像.
2.1 直接映射直接映射即数据不经过处理, 直接映射到图像完成绘制. 直接映射绘制是出现最早的绘制方法, 早在20世纪初, Whiting[28]就采用此方法将星球绘制成图像来展示星系图用于天文学生的教学, 并且此方法也是目前常用的绘制方法之一.
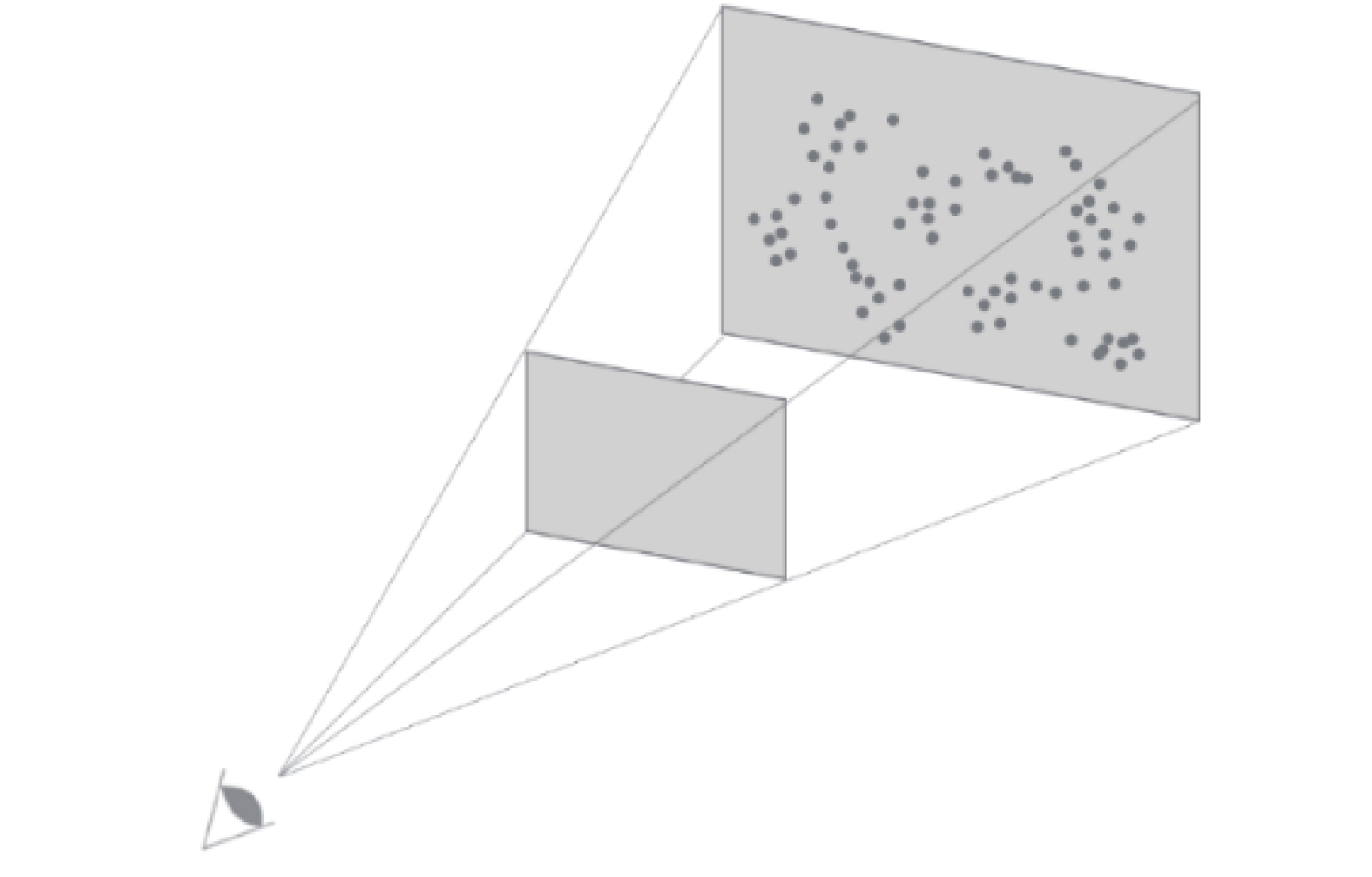
对于数值模拟为网格数据的2D图像绘制, 仅需要将三维的网格数据处理成二维网格, 然后根据图像大小进行映射即可完成数据的绘制, 过程示意图如图2所示.
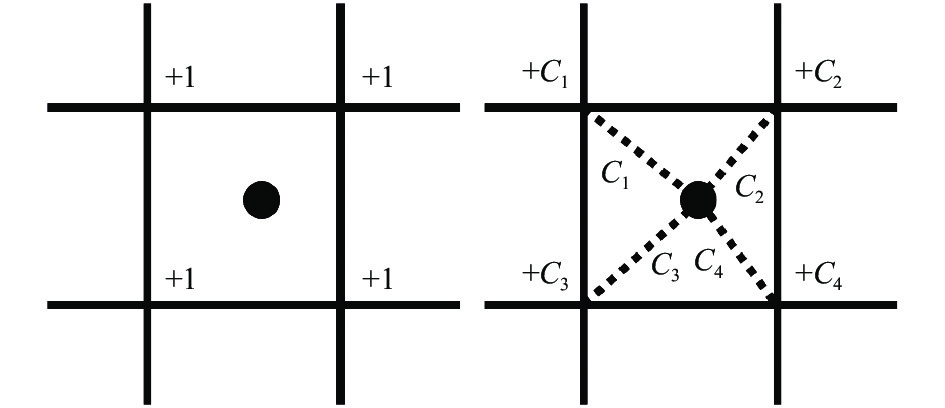
对于离散数据的2D图像绘制, 需要将粒子数据进行转换, 转换为均匀网格数据然后进行映射以完成粒子数据的绘制. 如图3所示, 展示的是粒子数据常用的两种转换方法. 每个粒子数据根据空间坐标属性映射到对应的均匀网格上, 所在网格的顶点将会增加相应的属性值.
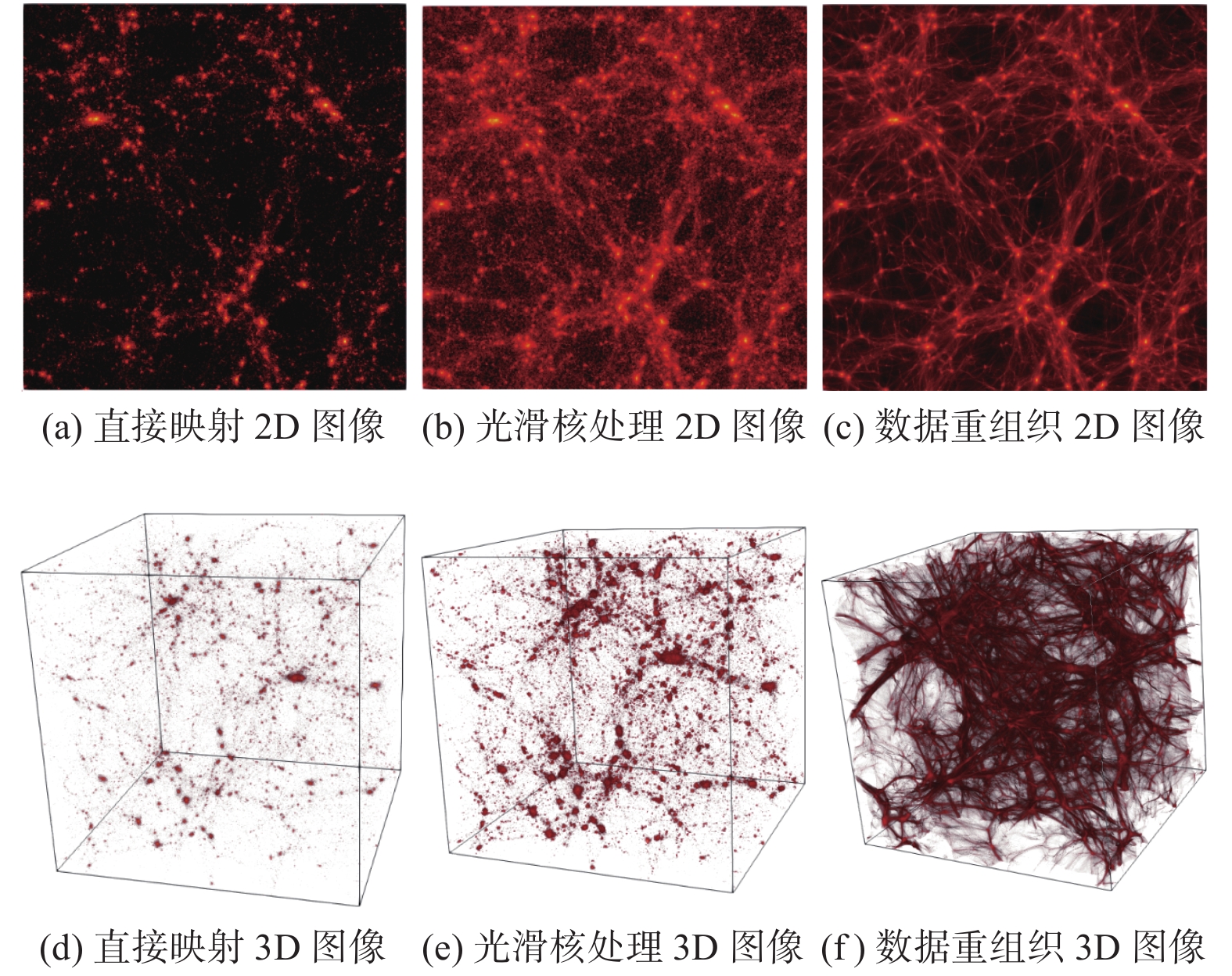
对于3D图像的绘制, 网格数据可以转换成体数据然后采用体绘制, 而粒子数据3D图像绘制也是将粒子转换成空间网格数据然后进行体绘制. 直接映射的可视化效果的2D图像和3D图像如图4(a)和图4(d)所示. 直接映射是最简单且效率最高的绘制方法, 但绘制图像的效果一般.
|
图 2 网格映射示意图 |
|
图 3 粒子映射示意图 |
|
图 4 不同绘制算法效果展示图 |
2.2 光滑核处理
数据直接映射的绘制效果一般, 为了提高绘制效果, 通常采用光滑核处理, 常用的光滑核为高斯光滑, 高斯分布函数公式如式(1)所示.
| $f(x) = \frac{1}{{\sqrt {2{\text{π}} } \sigma }}\exp \left( { - \frac{{{{(x - u)}^2}}}{{2{\sigma ^2}}}} \right) $ | (1) |
在使用过程中, 可以通过控制高斯分布函数中的标准差
使用光滑核函数对数据进行处理时, 针对于网格数据通常是对原始数据进行处理, 经过处理后的数据再经过直接映射然后完成数据的绘制. 针对于粒子数据, 采用的方式是将空间中的每个粒子转换成空间高斯分布函数, 然后再进行均匀网格的转换. 此外, 当把粒子转换成空间高斯分布函数时, 也可以采用抛雪球算法[29], 即将每个代表粒子的空间高斯分布直接抛到图像上进行绘制. 图4(b)和 图4(e)展示的为光滑核处理后的可视化图像结果, 从图像上可以看出光滑核处理后的绘制图像在结构表现上更加丰富, 可视化效果优于直接映射.
2.3 数据重组织数据重组织绘制通常用于天文模拟中粒子数据的绘制, 即将粒子数据重组成其他形态再进行映射和绘制. 目前最常使用的方法是Kaehler等[30]提出的可视化方法, 将粒子组建成四面体网格然后进行绘制.
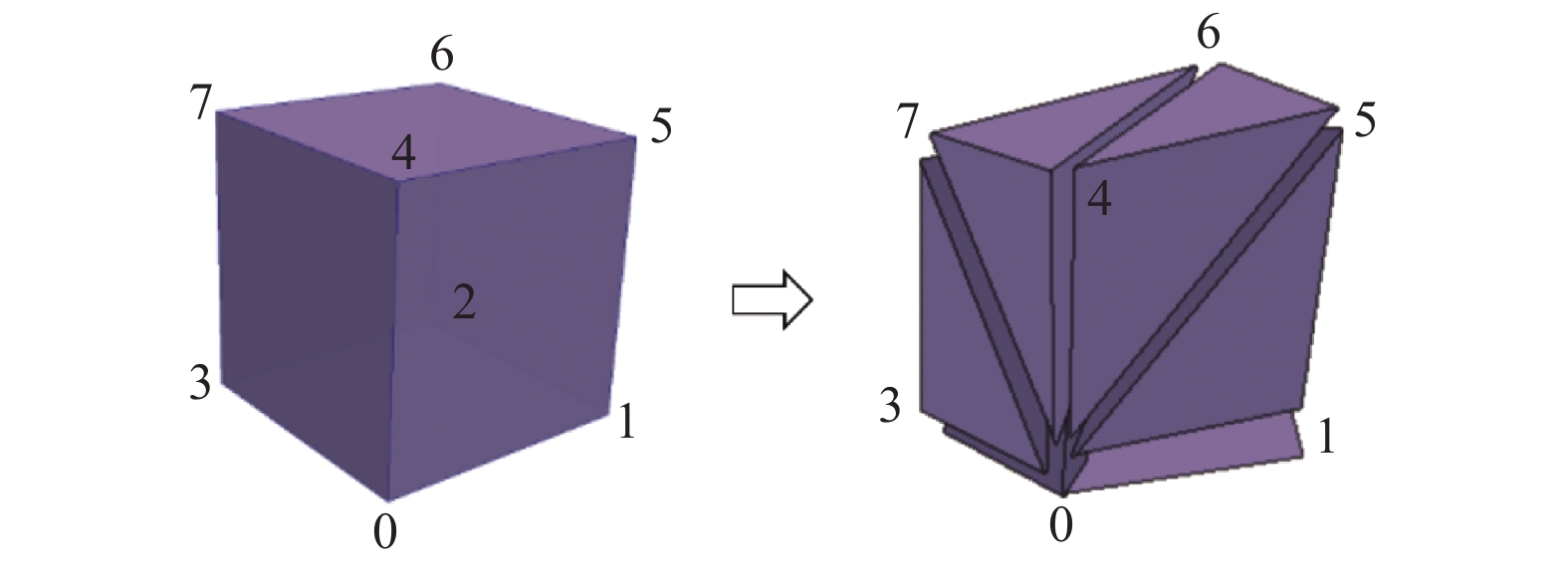
四面体网格算法是在模拟的初始时刻, 根据粒子的位置进行划分, 即空间上相邻8个粒子组成一个六面体, 然后将六面体切分成6个四面体, 每个四面体之间没有相交, 四面体的构建示意图如图5所示. 由于每个粒子会出现在8个六面体的顶点上, 因此在切分后, 每个粒子会出现在多个四面体的顶点, 空间内四面体通过顶点粒子相连接而构造成了四面体空间网格.
|
图 5 四面体构建示意图[30] |
在初始时刻完成四面体网格构造后, 记录每个四面体的粒子组成, 保持模拟过程中四面体组成粒子的不变, 每次绘制时以四面体为基本单位. 图4(c)和图4(f)展示的为四面体网格的绘制效果图, 从图像上可以看出四面体网格绘制效果非常好, 对宇宙特征结构展现的非常清晰, 可视化效果优于其他两种方法. 但是, 此方法也存在一定的限制, 即此方法仅限于对天文粒子数据的绘制, 并且绘制的时间远大于其他两种方法.
3 宇宙模拟数据可视化分析在模拟数据渲染的基础上和多种可视化任务的推动下, 发展出了多个可视化研究方向. 本节将依次探讨交互可视化、并行可视化、原位可视化和机器学习与可视化这些近年来的可视化研究热点, 并进行归纳和总结.
3.1 交互可视化交互可视化分析技术是使用交互式技术帮助用户进行模拟数据的分析, 其主要优势是通过交互完成特定的分析任务. 对于宇宙数值模拟的交互可视化分析根据分析的内容可以分为两类, 一类是对模拟数据的全局属性和参数进行分析, 另一类是对宇宙特定的结构进行分析.
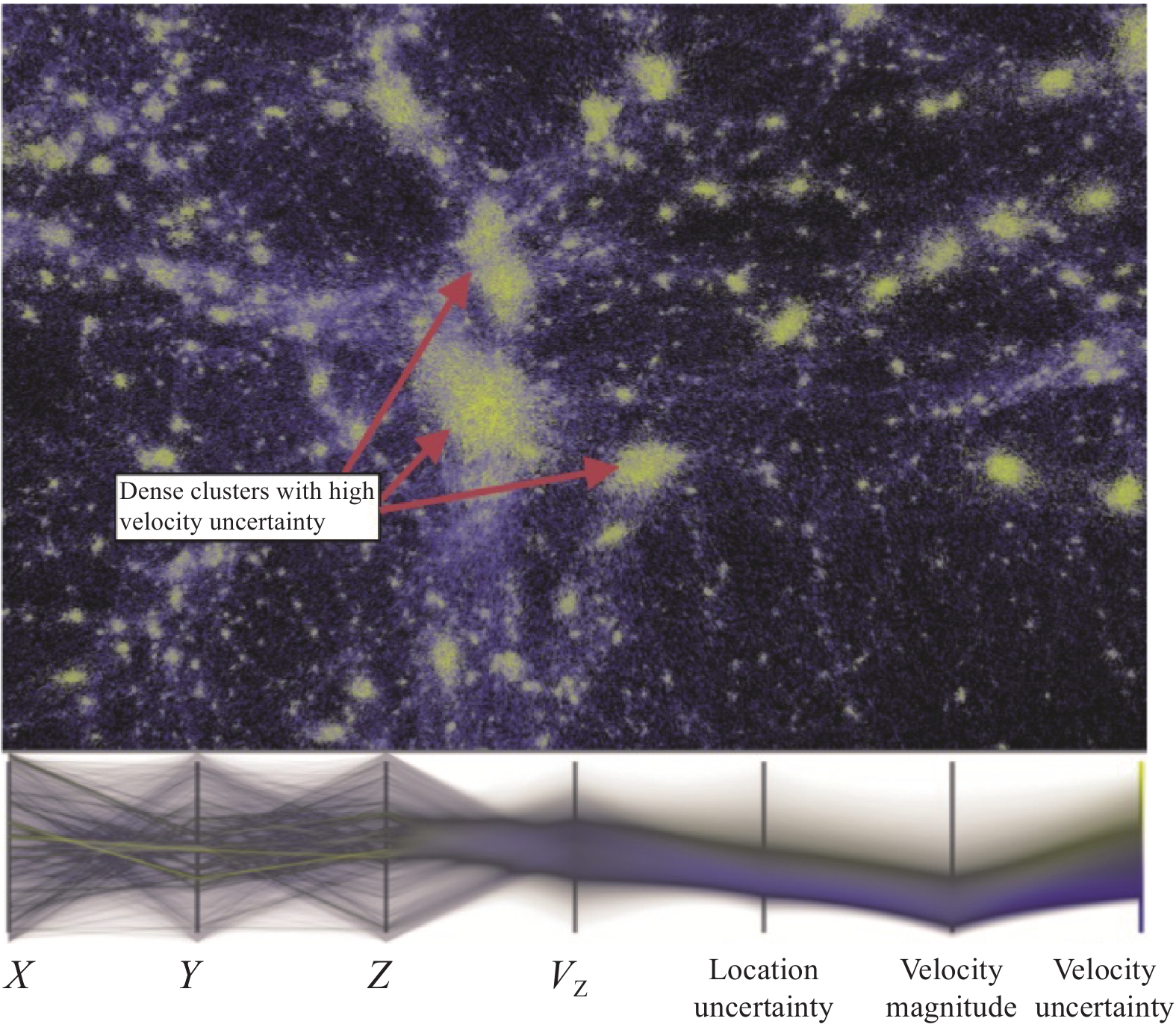
对模拟数据的属性和参数进行交互分析, 主要是对模拟数据的展示维度、展示区域、展示内容和时序属性等进行交互. 早期交互主要是对数据展示维度和时空位置等进行交互式分析, 例如Swayne等[31]设计了一个数据可视化系统用于展示高维空间中粒子数据并且允许用户进行旋转、区域选择和颜色调整等操作. 此外, Teuben等[32]和Price等[33]也实现类似工作, 即使用键盘和鼠标作为交互设备, 通过用户的交互操作对数据展示维度、展示区域和颜色映射等进行调整. 早期的交互式分析着重于对展示内容维度和展示区域的交互, 以帮助科学家更快的了解模拟数据. 随着研究的发展, 一些工作开始关注于对数据进行时序属性的分析. Haroz等[34]通过可视化系统来对不同的模拟的多个属性的时序差异进行分析. 如图6所示, 用户可以通过平行坐标轴来实时选择重要特征进而深入分析. 此外, Zhao等[35]通过一种交互粒子的图像生成算法展示模拟数据中高质量时序图像, 用来分析数据的时序特征. 从总体上来说, 对全局属性交互分析的主要目标是帮助用户了解数据并发现全局属性的异常特征.
|
图 6 不同模拟间的多属性时序差异分析[34] |
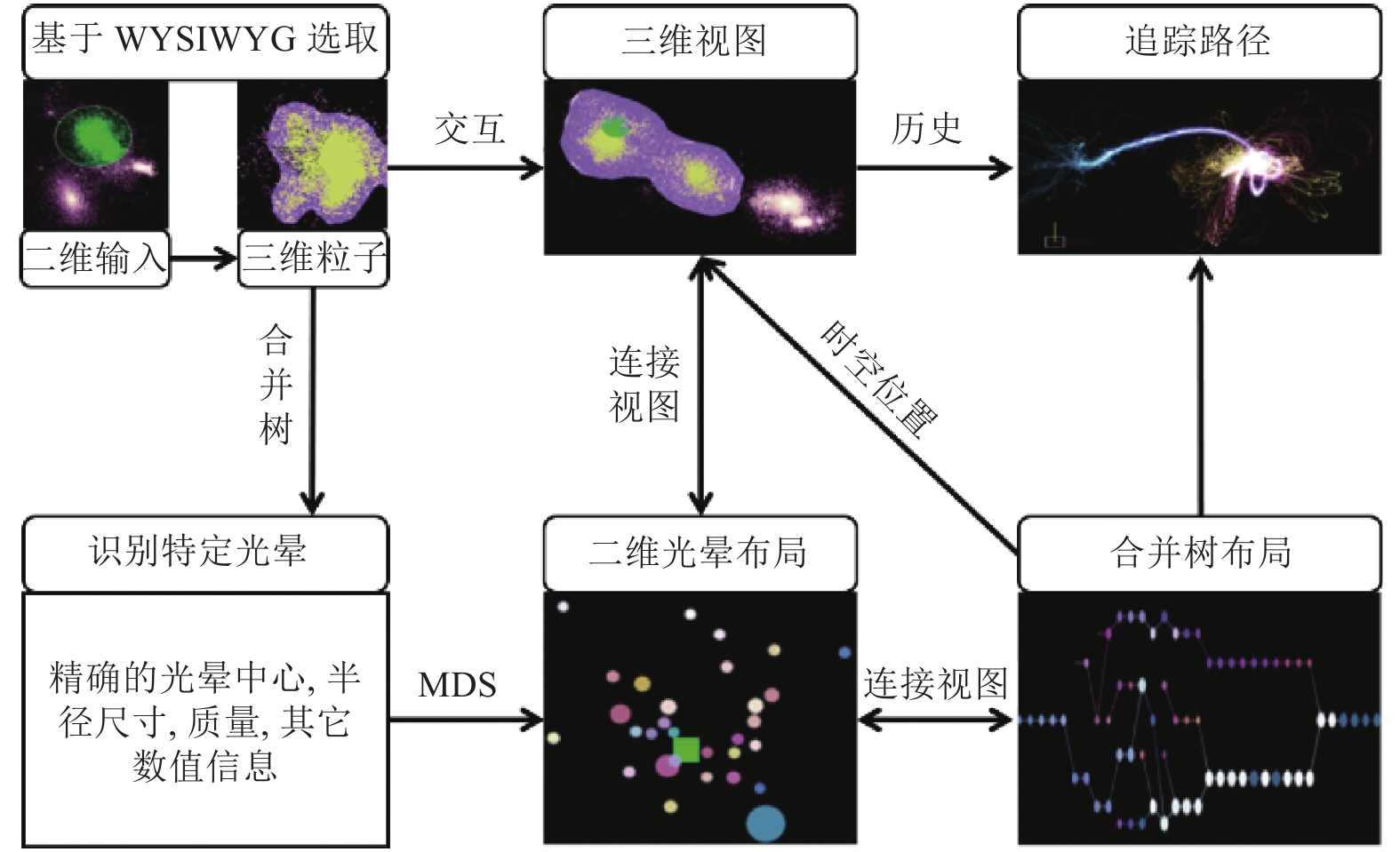
另一类是对宇宙特定的结构进行分析, 通常分析的目标结构集中在暗晕. 暗晕是模拟中由于粒子聚合而形成的密度高点, 是物质的三维塌缩而形成的. 对于暗晕的分析, 根据交互对象可以分为分析区域的选择和分析目标的选择. 分析区域的交互选择即用户通过交互操作对展示的目标区域进行选择[36-39]. 例如Shan等[36]通过开发可视化系统分析暗晕的合并演化历史, 如图7所示. 用户通过2D的交互操作选取目标分析区域, 系统基于交互参数来生成目标区域的暗晕3D的演化过程. Rapp等[39]通过概率密度函数来拟合大规模宇宙模拟数据, 进而可以有效地对结构进行表示, 通过对概率模拟函数的可视化和交互来达到对区域数据交互式分析的目的. 分析目标的交互选择, 即用户通过交互操作来显示单个暗晕的演化过程和物理属性[40-42]. 例如Almryde等[40]通过可视化展示了暗物质晕的合并树的演化历史, 允许用户通过交互操作从合并树中选择单独的暗晕来分析单个暗晕的属性. 从总体上来说, 对宇宙特定结构交互分析的主要目标是帮助用户分析单个或者区域的暗晕演化过程, 进而利用可视化图像更加深入直观的了解演化过程. 此外, Hanula等[41]通过构建一个沉浸式的可视化软件来对宇宙模拟数据进行交互和分析, 该软件通过多个分析视图的交互和联动展示, 帮助领域专家对模拟数据进行时序结构演化分析. 同时, 还可以帮助专家对特定暗晕的形成和演化进行交互和探索.
|
图 7 区域暗晕交互式分析流程图[36] |
3.2 并行可视化
计算机硬件的发展为并行计算提供了有力的支撑, 并行计算的发展也为可视化提供了新的技术. 为了处理和绘制大规模的模拟数据, 越来越多研究中采用了并行计算. 根据并行加速的内容, 可以将并行可视化分为两类, 第一类是并行的数据处理, 第二类是并行的数据绘制.
对于并行的数据处理, 即通过并行计算对大规模数据进行快速预处理, 将处理后的数据进行可视化展示. 例如Woodring等[43]基于ParaView[44]可视化软件设计了一个并行的数据处理模块, 并行的运行暗晕寻找算法和实时的暗晕分布展示, 利用并行计算可以极大提高数据处理的速度, 加速对暗晕的分析过程. 此外, Jin等[45]利用由多个GPU和CPU组成的超算, 使用了MPI[46]和OpenMP[47]框架对数据的坐标转换、归一化、旋转等操作进行加速处理. Tallada等[48]介绍了一款基于Hadoop的Web应用CosmoHub, 可以对大量宇宙数据集进行交互式探索和分发. 它正在为几个大型国际合作项目提供数据支持, 如欧几里得空间任务、暗能量调查(DES)、加速宇宙调查(PAUS)和马勒斯特姆科学研究所(MICE)的数值模拟等. 目前, 对109大小数据集的在线探索可以在几十秒的时间尺度内完成. 总体来说利用并行计算对数据进行处理的目标是通过并行的数据处理算法快速生成可视化的数据, 以达到可以处理和分析大规模数据的目的.
对于并行的数据绘制, 即利用并行技术对数据的绘制进行加速. 例如Kaehler等[49]设计实现了基于GPU的辅助光线投射算法, 利用GPU的并行加速生成局部精细网格, 该算法可以获得高质量体绘制结果. Dykes等[50]设计实现了基于GPU的Splotch方法, 通过将粒子数据进行分组使CPU和GPU可以同时对数据进行并行处理以加速Splotch的绘制过程. Rizzi等[51]实现了一种基于GPU的点绘制技术, 通过对粒子进行层次重组并使用动态的绘制任务分解, 用以加速大规模粒子数据的绘制. 此外, 也有许多相关的研究利用并行计算来加速渲染过程[52,53]. 利用并行计算对绘制进行加速的目标是能够对大规模数据进行绘制, 不仅提高绘制效率也可以获得高质量的图像.
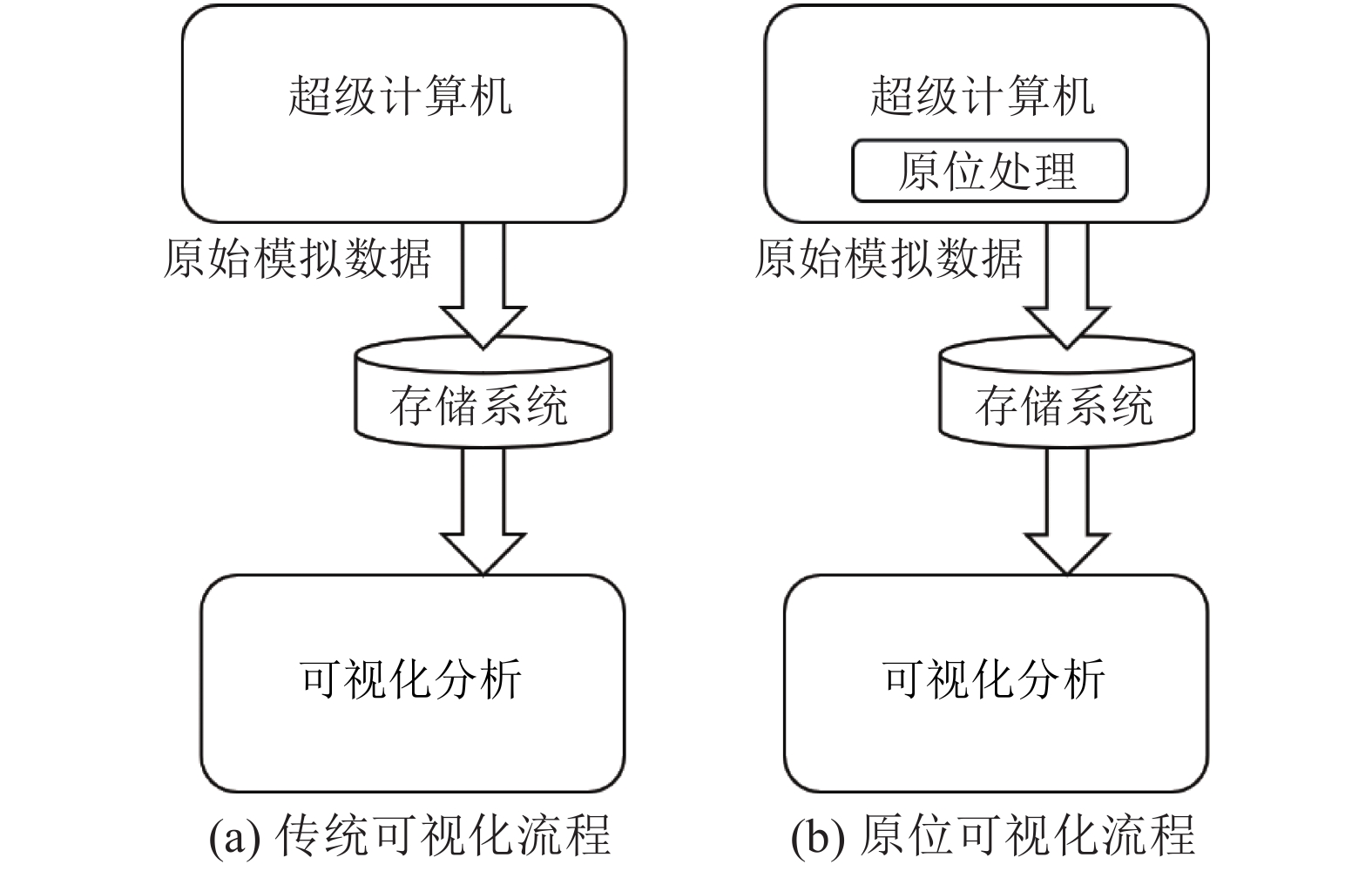
3.3 原位可视化随着超级计算机的发展, 模拟的规模越来越大, 但存储能力的增长却难以满足大规模模拟的数据存储要求. 由于存储资源的限制, 无法将所需的全部模拟数据进行保存、分析和可视化. 原位可视化是解决这种问题的最有效的方法. 原位可视化即在模拟运行的过程中, 在模拟的计算节点上对数据进行原位处理, 将处理后的数据进行保存以供事后的可视化分析. 原位可视化与传统后处理形式的可视化在流程上的对比如图8所示[54]. 原位可视化中数据在内存中就被可视化程序所处理, 处理后保存的数据量远小于原始数据, 因此可以解决I/O瓶颈的问题和存储限制的难点, 为可视化分析超大规模模拟的数据提供有效的方法. 原位可视化从原位处理的方式上可以分为3类, 即原位数据压缩处理、原位的图像渲染处理和原位特征提取处理.
原位数据压缩处理是通过使用压缩或者采样算法在原位进行处理以降低数据量, 进而可以保存更多的数据. 例如Woodring等[55]使用层次化的随机采样算法对超大规模的模拟数据进行原位采样处理, 算法通过KD树在每个计算节点对粒子数据进行分块, 在块内采用随机采样, 同时通过控制每个块的大小来调整压缩率. 此算法在计算节点之间不需要进行通信, 具有很高的并行效率和可扩展性, 通过层次化的随机采样可以极大降低数据的存储, 为大规模数据的可视化和分析提供了有力的支持. 但算法也存在一些限制, 随机采样丢失了许多细节, 使得高精度的分析误差较大, 并且由于粒子时序关系的丢失, 时序分析和时序可视化也需要额外的处理. Hazarika等[56]提出了一种抽样策略, 通过使用多个跨空间域的PCA模型获取全局多元关系可以在降低存储多变量模拟数据占用的同时保护多变量之间的关系. 也有一些研究探讨了压缩算法在原位的有效性, Zeyen等[57]比较了多种最新的压缩算法, 探讨了原位可视化中压缩算法的有效性, 他们通过对230个粒子数据的压缩实验, 测试了多个最先进的有损压缩算法和无损压缩算法的效果和效率. 通过对比, 他们指出在天文专家认可的最大误差下, 这些算法中SZ压缩算法[58]的压缩率最高, 可以达到46.72%. 压缩算法虽然可以保证数据的质量, 但其压缩率还是难以满足超大规模的原位处理要求.
|
图 8 传统可视化与原位可视化对比图[54] |
原位的图像渲染处理是模拟运行过程中, 在原位阶段运行数据绘制算法, 将原始数据直接可视化, 仅需要存储或者传输图像数据, 从而极大地降低数据量. Whitlock等[59]通过对可视化工具VisIt进行扩展, 在模拟过程中渲染模块与模拟程序同时进行运行, 并在用户控制下实时地对数据进行渲染和传输. 这种原位的图像渲染方式, 可以处理超大规模的模拟数据, 解决了I/O的瓶颈和存储的限制. 但仅存储和使用图像数据而丢弃原始数据, 使得用户难以进行后续的交互式探索和数据统计分析计算.
原位特征提取处理是通过使用数据分析或处理算法, 将专家最关心的特征进行提取和保存, 减少不必要的存储以达到超大规模原位可视化分析的目的. Li等[60]采用了概率密度模型在原位阶段对粒子数据进行特征提取, 该算法通过KD树对每个计算节点内数据进行划分, 划分后使用高斯混合模型对划分后的数据进行特征提取, 并使用模型评估、模型优化等手段提高特征数据的质量. 经过原位处理后, 仅需要保存高斯混合模型的参数, 并且可以通过蒙特卡洛算法重构粒子数据以支持数据可视化和物理属性计算. 该方法在原位处理时, 计算节点之间相互独立, 不需要额外的通信, 所以可扩展性较高. 同时算法的压缩率可达到1.3%, 并在此压缩率下可以重构高质量的数据用以可视化分析. 图9中展示了基于模型参数重构后粒子数据与原始数据的对比可视化结果, 从可视化效果可以看出, 重构数据可视化图像几乎与原始数据可视化图像一致. 类似地, Takle等[61]的工作也是采用了原位特征提取方法, 在模拟过程中追踪暗晕的演化历史并在模拟过程中完成合并树的建立. 通过这种特征追踪的方法可以高效地对暗晕结构进行分析和可视化. 原位特征提取处理的方式可以非常有效地解决I/O的瓶颈和存储的限制, 但此类研究通常针对特定的问题, 所以算法的通用性有待提高.

|
图 9 原始数据与特征提取算法的对比可视化[60] |
3.4 机器学习与可视化
机器学习作为一种有效的数据处理和分析手段, 已经应用在越来越多的领域. 随着深度学习研究发展, 极大的推动了其他领域深度学习相关应用研究的产生. 在宇宙数值模拟可视化研究中, 机器学习算法的应用也逐渐成为一个热点.
Preston等[62]研究了基于聚类算法合并树的数据可视化方法, 利用可视化技术分析在天文数据中应用聚类算法的效果, 帮助使用者对聚类结果更加了解, 提高数据分析的准确性和发现异常特征的能力. Wang等[63]提出了统计超分辨率方法来提高大规模宇宙数值模拟数据中分析和可视化的能力, 并且可以解决超大规模数据的传输和保存等数据处理瓶颈. 算法使用高斯混合模型对数据进行表达, 并利用小规模的模拟数据来构建先验知识, 然后通过算法来建立从低分辨率到高分辨率数据的映射关系. 在数据可视化时, 利用映射关系从低分辨率的数据中构建高分辨率的数据以获得高质量的可视化效果.
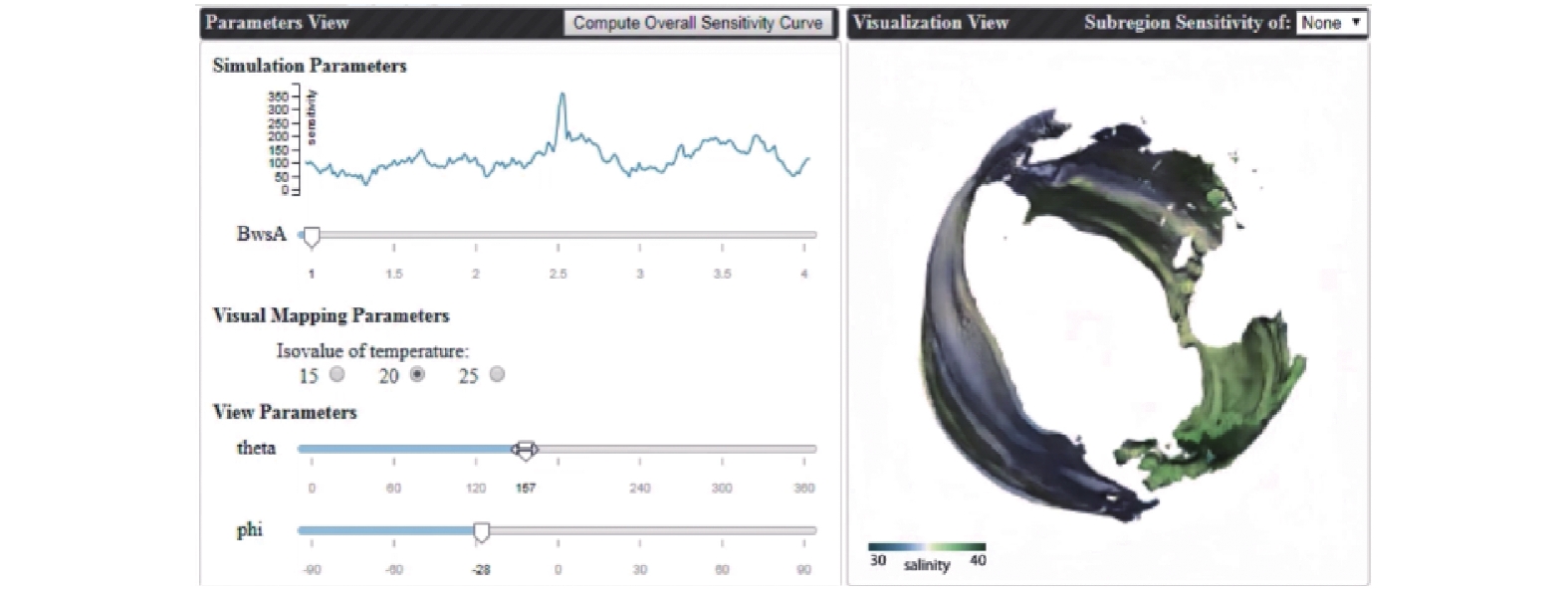
He等[64]提出了一个基于深度学习神经网络的模拟替代模型InSituNet, 它可以为科学家快速探索和预估不同模拟参数下的模拟结果. InSituNet使用了生成式对抗网络(GAN)[65]来处理模拟数据, 神经网络利用多组科学模拟数据学习模拟参数和可视化参数到可视化结果的映射关系. 用户可以使用训练后深度学习模型来仿真在不同的可视化参数和模拟参数下的可视化图像, 这可以减少不必要的模拟并节约超算的计算资源. 此外, 通过燃烧模拟、海洋模拟和宇宙数值模拟的多组数据测试, InSituNet表现出了良好的效果. 图10展示的为InSituNet可视化软件界面, 用户可以通过对左侧参数视图进行参数调整, 右侧可视化视图会实时展示设定参数下对应的可视化预测结果.
|
图 10 InSituNet可视化软件界面[64] |
总体来说, 机器学习算法作为数据分析和数据处理的手段, 支撑了可视化分析. 通过机器学习算法和可视化技术的结合, 极大提高数据分析效率.
4 研究趋势与挑战超级计算机的发展使得数值模拟的规模会继续增加, 特别是E级超级计算机的到来为科学数据的可视化分析带来新的机遇和挑战, 可视化作为分析超大规模数值模拟数据最有效的手段在未来的作用也将越来越突出. 在数据分析需求的推动下, 宇宙数值模拟可视化研究将会呈现新的发展趋势.
深度学习相关的研究在许多领域已崭露头角, 特别是近些年来深度神经网络的发展和应用, 极大的提高数据分析的能力与效率. 当前已经出现了一些将深度神经网络用于天文数据可视化分析的探索, 并取得非常好的效果. 未来在天文数据可视化中的应用会越来越多, 例如可视化技术结合深度神经网络对天文数据中特征结构的识别、追踪、分类和预测等将会是一个重要的研究方向.
超大规模数据分析的需求使得原位可视化研究越来越迫切, 随着E级计算的到来, 大规模数据分析的挑战会日益突出. 原位可视化作为一种有效分析超大规模数据的手段已经取得了多项研究成果, 但目前仍存在一些问题. 例如, 如何实现在原位可视化分析中基于原位的时序数据分析方法, 以及如何设计通用性的原位分析框架. 此外, 数据分析算法的发展(如数据挖掘算法、深度神经网络、并行数据处理等)也为原位可视化分析提供了新的数据分析思路.
在可视化交互方面, 目前还是多以鼠标和键盘的方式进行交互, 新型的交互设备将会为交互分析提供新的方法, 例如增强现实设备和虚拟现实设备的出现为科学数据的展示和交互提供了新的工具. 增强现实设备和虚拟现实设备提供的三维沉浸式环境适合展示科学模拟数据, 特别是天文模拟中模拟对象本就是三维空间, 这种三维沉浸式环境可以更加真实的展示模拟对象的演化特征, 并且带来的交互方式提高了数据分析的效率. 因此, 交互式设备的发展为科学数据分析中的交互方法带来新的研究内容.
5 结语本文首先介绍了宇宙数值模拟的发展和目前常用的数据绘制方法, 并在此基础上根据近年来宇宙数值模拟可视化研究的内容讨论了当前主要的可视化研究方向: 交互可视化、并行可视化、原位可视化、机器学习与可视化. 通过展示每个研究方向的具体案例, 归纳总结了当前的研究状态, 并根据发展趋势讨论了下一步研究的方法和方向.
可视化作为最有效的数据分析手段, 在宇宙模拟数据分析中已经取得了大量的研究成果, 但目前该领域仍存在许多需求和挑战, 仍需进一步的研究和发展.
| [1] |
冯珑珑, 朱维善. 现代宇宙学中的数值模拟技术和应用. 中国科学: 物理学 力学 天文学, 2013, 43(6): 687-707. |
| [2] |
Potter D, Stadel J, Teyssier R. PKDGRAV3: Beyond trillion particle cosmological simulations for the next era of galaxy surveys. Computational Astrophysics and Cosmology, 2017, 4(1): 2. DOI:10.1186/s40668-017-0021-1 |
| [3] |
Springel V, White SDM, Jenkins A, et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature, 2005, 435(7042): 629-636. DOI:10.1038/nature03597 |
| [4] |
Gao L, Navarro JF, Frenk CS, et al. The phoenix project: The dark side of rich galaxy clusters. Monthly Notices of the Royal Astronomical Society, 2012, 425(3): 2169-2186. DOI:10.1111/j.1365-2966.2012.21564.x |
| [5] |
Wang J, Bose S, Frenk CS, et al. Universal structure of dark matter haloes over a mass range of 20 orders of magnitude. Nature, 2020, 585(7823): 39-42. DOI:10.1038/s41586-020-2642-9 |
| [6] |
Peebles PJE. Structure of the coma cluster of galaxies. Astronomical Journal, 1970, 75: 13-20. DOI:10.1086/110933 |
| [7] |
Groth EJ, Peebles PJE. N-body studies of the clustering of galaxies. Bulletin of the American Astronomical Society, 1975, 7: 425.
|
| [8] |
Miyoshi K, Kihara T. Development of the correlation of galaxies in an expanding universe. Astronomical Society of Japan, Publications, 1975, 27(2): 333-346. |
| [9] |
White SDM. The dynamics of rich clusters of galaxies. Monthly Notices of the Royal Astronomical Society, 1976, 177(3): 717-733. DOI:10.1093/mnras/177.3.717 |
| [10] |
Aarseth SJ, Gott III JR, Turner EL. N-body simulations of galaxy clustering I. Initial conditions and galaxy collapse times. The Astrophysical Journal, 1979, 228: 664-683. |
| [11] |
Efstathiou G, Eastwood JW. On the clustering of particles in an expanding universe. Monthly Notices of the Royal Astronomical Society, 1981, 194(3): 503-525. DOI:10.1093/mnras/194.3.503 |
| [12] |
Davis M, Efstathiou G, Frenk CS, et al. The evolution of large-scale structure in a universe dominated by cold dark matter. The Astrophysical Journal, 1985, 292: 371-394. DOI:10.1086/163168 |
| [13] |
White SDM, Frenk CS, Davis M, et al. Clusters, filaments, and voids in a universe dominated by cold dark matter. The Astrophysical Journal, 1987, 313: 505-516. DOI:10.1086/164990 |
| [14] |
Carlberg RG, Couchman HMP. Mergers and bias in a cold dark matter cosmology. The Astrophysical Journal, 1989, 340: 47-68. DOI:10.1086/167375 |
| [15] |
Suto Y, Suginohara T. Redshift-space correlation functions in the cold dark matter scenario. The Astrophysical Journal, 1991, 370: L15-L18. DOI:10.1086/185966 |
| [16] |
Warren MS, Quinn PJ, Salmon JK, et al. Dark halos formed via dissipationless collapse. I: Shapes and alignment of angular momentum. The Astrophysical Journal, 1992, 399: 405-425. |
| [17] |
Gelb JM, Bertschinger E. Cold dark matter. I: The formation of dark halos. The Astrophysical Journal, 1994, 436: 467-490. |
| [18] |
Jenkins A, Frenk CS, Pearce FR, et al. Evolution of structure in cold dark matter universes. The Astrophysical Journal, 1998, 499(1): 20-40. DOI:10.1086/305615 |
| [19] |
Governato F, Babul A, Quinn T, et al. Properties of galaxy clusters: Mass and correlation functions. Monthly Notices of the Royal Astronomical Society, 1999, 307(4): 949-966. DOI:10.1046/j.1365-8711.1999.02706.x |
| [20] |
Bode P, Ostriker JP, Turok N. Halo formation in warm dark matter models. The Astrophysical Journal, 2001, 556(1): 93-107. DOI:10.1086/321541 |
| [21] |
Colberg JM, White SDM, Yoshida N, et al. Clustering of galaxy clusters in cold dark matter universes. Monthly Notices of the Royal Astronomical Society, 2000, 319(1): 209-214. |
| [22] |
Wambsganss J, Bode P, Ostriker JP. Giant arc statistics in concord with a concordance lambda cold dark matter universe. The Astrophysical Journal, 2004, 606(2): L93-L96. DOI:10.1086/421459 |
| [23] |
Li M, Pan J, Gao L, et al. Bulk flow of halos in ΛCDM simulation. The Astrophysical Journal, 2012, 761(2): 151-161. DOI:10.1088/0004-637X/761/2/151 |
| [24] |
Teyssier R, Pires S, Prunet S, et al. Full-sky weak-lensing simulation with 70 billion particles. Astronomy & Astrophysics, 2009, 497(2): 335-341. |
| [25] |
Angulo RE, Springel V, White SDM, et al. Scaling relations for galaxy clusters in the Millennium-XXL simulation. Monthly Notices of the Royal Astronomical Society, 2012, 426(3): 2046-2062. DOI:10.1111/j.1365-2966.2012.21830.x |
| [26] |
Kim J, Park C, Rossi G, et al. The new horizon run cosmological N-body simulations
. Journal of the Korean Astronomical Society, 2011, 44(6): 217-234. DOI:10.5303/JKAS.2011.44.6.217 |
| [27] |
Alimi JM, Bouillot V, Rasera Y, et al. DEUS full observable Λ CDM universe simulation: The numerical challenge. arXiv: 1206.2838, 2012.
|
| [28] |
Whiting SF. Use of graphs in teaching astronomy. Popular Astronomy, 1905, 13: 185-190. |
| [29] |
Westover L. Interactive volume rendering. Proceedings of the 1989 Chapel Hill Workshop on Volume Visualization. Chapel Hill: ACM, 1989. 9–16.
|
| [30] |
Kaehler R, Hahn O, Abel T. A novel approach to visualizing dark matter simulations. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(12): 2078-2087. DOI:10.1109/TVCG.2012.187 |
| [31] |
Swayne DF, Cook D, Buja A. XGobi: Interactive dynamic data visualization in the X Window system. Journal of Computational and Graphical Statistics, 1998, 7(1): 113-130. |
| [32] |
Teuben PJ, Hut P, Levy S, et al. Immersive 4-D interactive visualization of large-scale simulations. In: Harnden FR Jr, Primini FA, Payne HE, eds. Astronomical Data Analysis Software and Systems X. San Francisco: ASP, 2001, 238: 499. |
| [33] |
Price DJ. SPLASH: An interactive visualisation tool for smoothed particle hydrodynamics simulations. Publications of the Astronomical Society of Australia, 2007, 24(3): 159-173. DOI:10.1071/AS07022 |
| [34] |
Haroz S, Heitmann K. Seeing the difference between cosmological simulations. IEEE Computer Graphics and Applications, 2008, 28(5): 37-45. DOI:10.1109/MCG.2008.101 |
| [35] |
Zhao K, Sakamoto N, Koyamada K. Using interactive particle-based rendering to visualize a large-scale time-varying unstructured volume with mixed cell types. 2017 IEEE Pacific Visualization Symposium (PacificVis). Seoul: IEEE, 2017. 185–189.
|
| [36] |
Shan GH, Xie MJ, Li FA, et al. Interactive visual exploration of halos in large-scale cosmology simulation. Journal of Visualization, 2014, 17(3): 145-156. DOI:10.1007/s12650-014-0206-5 |
| [37] |
Preston A, Ghods R, Xie JR, et al. An integrated visualization system for interactive analysis of large, heterogeneous cosmology data. 2016 IEEE Pacific Visualization Symposium (PacificVis). Taipei: IEEE, 2016. 48–55.
|
| [38] |
Scherzinger A, Brix T, Drees D, et al. Interactive exploration of cosmological dark-matter simulation data. IEEE Computer Graphics and Applications, 2017, 37(2): 80-89. DOI:10.1109/MCG.2017.20 |
| [39] |
Rapp T, Peters C, Dachsbacher C. Visual analysis of large multivariate scattered data using clustering and probabilistic summaries. IEEE Transactions on Visualization and Computer Graphics, 2021, 27(2): 1580-1590. DOI:10.1109/TVCG.2020.3030379 |
| [40] |
Almryde KR, Forbes AG. Halos in a dark sky: Interactively exploring the structure of dark matter halo merger trees. 2015 IEEE Scientific Visualization Conference (SciVis). Chicago: IEEE, 2015. 73–77.
|
| [41] |
Hanula P, Piekutowski K, Uribe C, et al. Cavern halos: Exploring spatial and nonspatial cosmological data in an immersive virtual environment. 2015 IEEE Scientific Visualization Conference (SciVis). Chicago: IEEE, 2015. 87–99.
|
| [42] |
Takle J, Silver D, Kovacs E, et al. Visualization of multivariate dark matter halos in cosmology simulations. 2013 IEEE Symposium on Large-scale Data Analysis and Visualization (LDAV). Atlanta: IEEE, 2013. 131–132.
|
| [43] |
Woodring J, Heitmann K, Ahrens J, et al. Analyzing and visualizing cosmological simulations with ParaView. The Astrophysical Journal Supplement Series, 2011, 195(1): 11. DOI:10.1088/0067-0049/195/1/11 |
| [44] |
Henderson A, Ahrens J, Law C. The Paraview Guide. New York: Kitware, 2004.
|
| [45] |
Jin ZF, Krokos M, Rivi M, et al. High-performance astrophysical visualization using Splotch. Procedia Computer Science, 2010, 1(1): 1775-1784. DOI:10.1016/j.procs.2010.04.199 |
| [46] |
Clarke L, Glendinning I, Hempel R. The MPI message passing interface standard. In: Decker KM, Rehmann RM, eds. Programming Environments for Massively Parallel Distributed Systems. Birkhäuser, Basel: Springer, 1994.213–218.
|
| [47] |
Chandra R, Dagum L, Kohr DR, et al. Parallel Programming in OpenMP. San Francisco: Morgan Kaufmann Publishers, 2001.
|
| [48] |
Tallada P, Carretero J, Casals J, et al. CosmoHub: Interactive exploration and distribution of astronomical data on hadoop. Astronomy and Computing, 2020, 32: 100391. DOI:10.1016/j.ascom.2020.100391 |
| [49] |
Kaehler R, Wise J, Abel T, et al. GPU-assisted raycasting for cosmological adaptive mesh refinement simulations. In: Raghu M, Torsten M, eds. Volume Graphics. The Eurographics Association, 2006. 103–110.
|
| [50] |
Gheller C, Rivi M, Krokos M, et al. CUDA-splotch: GPU visualization of astrophysical data. Breast Cancer Research & Treatment, 2013, 475(1): 103.
|
| [51] |
Rizzi S, Hereld M, Insley J, et al. Large-scale parallel visualization of particle-based simulations using point sprites and level-of-detail. Proceedings of the 15th Eurographics Symposium on Parallel Graphics and Visualization. Argonne: Argonne National Lab., 2015. 1–10.
|
| [52] |
Hassan AH, Fluke CJ, Barnes DG, et al. Tera-scale astronomical data analysis and visualization. Monthly Notices of the Royal Astronomical Society, 2013, 429(3): 2442-2455. DOI:10.1093/mnras/sts513 |
| [53] |
Yang L, Szalay A. A GPU-based visualization method for computing dark matter annihilation signal. Astronomical Data Analysis Software and Systems XXII. San Francisco: Astronomical Society of the Pacific, 2013, 475: 73. |
| [54] |
单桂华, 田东, 谢茂金, 等. 千万亿次科学计算的原位可视化. 计算机辅助设计与图形学学报, 2013, 25(3): 286-293. DOI:10.3969/j.issn.1003-9775.2013.03.002 |
| [55] |
Woodring J, Ahrens J, Figg J, et al. In-situ sampling of a large-scale particle simulation for interactive visualization and analysis. Computer Graphics Forum, 2011, 30(3): 1151-1160. DOI:10.1111/j.1467-8659.2011.01964.x |
| [56] |
Hazarika S, Biswas A, Wolfram PJ, et al. Relationship-aware multivariate sampling strategy for scientific simulation data. 2020 IEEE Visualization Conference (VIS). Salt Lake City: IEEE, 2020. 41–45.
|
| [57] |
Zeyen M, Ahrens J, Hagen H, et al. Cosmological particle data compression in practice. Proceedings of the in situ Infrastructures on Enabling Extreme-Scale Analysis and Visualization. Denver: ACM, 2017. 12–16.
|
| [58] |
Di S, Cappello F. Fast error-bounded lossy HPC data compression with SZ. 2016 IEEE International Parallel and Distributed Processing Symposium (IPDPS). Chicago: IEEE, 2016. 730–739.
|
| [59] |
Whitlock B, Favre JM, Meredith JS. Parallel in situ coupling of simulation with a fully featured visualization system. Proceedings of the 11th Eurographics Conference on Parallel Graphics and Visualization. Llandudno: ACM, 2011.101–109.
|
| [60] |
Li G, Xu JY, Zhang TC, et al. Distribution-based particle data reduction for in-situ analysis and visualization of large-scale N-body cosmological simulations. 2020 IEEE Pacific Visualization Symposium (PacificVis). Tianjin: IEEE, 2020. 171–180.
|
| [61] |
Takle J, Heitmann K, Peterka T, et al. Abstract: Tracking and visualizing evolution of the universe: In situ parallel dark matter halo merger trees. 2012 SC Companion: High Performance Computing, Networking Storage and Analysis. Salt Lake City: IEEE, 2012. 1482–1483.
|
| [62] |
Preston A, Ma KL. Cluster-based visualization for merger tree data: The challenge of missing expectations. 2018 IEEE Scientific Visualization Conference (SciVis). Berlin: IEEE, 2018. 42–46.
|
| [63] |
Wang KC, Xu JY, Woodring J, et al. Statistical super resolution for data analysis and visualization of large scale cosmological simulations. 2019 IEEE Pacific Visualization Symposium (PacificVis). Bangkok: IEEE, 2019.303–312.
|
| [64] |
He WB, Wang JP, Guo HQ, et al. InSituNet: Deep image synthesis for parameter space exploration of ensemble simulations. IEEE Transactions on Visualization and Computer Graphics, 2020, 26(1): 23-33. |
| [65] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: ACM, 2014. 2672–2680.
|
 2021, Vol. 30
2021, Vol. 30