深度强化学习^[1]通过将深度学习^[2]与强化学习^[3]相结合, 在序贯决策问题上取得显著进展. 例如Atari 2600视频游戏^[4]、棋盘游戏^[5]、自动驾驶^[6]等领域. 深度学习的引入解决了传统强化学习在处理高维状态空间时所遇到的问题, 通过使用线性或非线性函数对强化学习中的值函数进行表示, 能直接从高维状态输入中学习到策略.

即便深度强化学习在很多复杂环境中取得突破, 但目前仍有一些问题影响着深度强化学习的发展^[7]. 其中样本效率问题是强化学习的挑战之一, 强化学习的学习过程是通过智能体与环境的相互作用, 探索未知的区域并获得数据样本, 再根据所获的数据样本进策略更新. 因而强化学习的学习过程中没有固定的数据集, 需要通过智能体与环境进行大量交互获取数据样本, 并依据样本不断改进策略, 最终才能适应环境以得到良好的策略. 这样会导致智能体需要消耗极大的时间成本用于获取数据样本, 特别是在现实环境中, 会承担很多风险与代价. 例如深度Q网络^[1]在Arcade Learning Environment (ALE)平台的游戏中需要大概两亿帧的状态转移样本(大约39天的实时游戏时间)来进行训练才能达到人类水平; 在自动驾驶等领域应用深度强化学习算法时, 不能冒险尝试多种情况, 使得获得样本的成本代价高; 在一些机器人控制研究中, 需要消耗大量的成本用于机器人与环境进行交互来获取数据等. 因此, 减少智能体与环境的交互次数显得尤为重要. 同时 如何对经验进行回放将会影响深度强化学习算法最终所训练出的策略的优劣, 选择不同的数据样本对学习最优策略产生的影响也将不同. 深度Q网络算法通过随机选择记忆回放单元中的样本进行训练, 这种方式能够打破样本之间的相关性, 为深度神 经网络提供独立同分布的样本, 但对每个样本进行同等对待的随机抽样方式显得并不高效.

国内外研究者对以上问题开展了研究. 一些研究者认为缺乏有效的探索会导致所生成的数据样本不能为学习最优策略提供良好的帮助, 需要通过改变探索策略生成出更利于学习的数据样本, 这样能在一定程度上减少智能体与环境交互的次数. 通过引入随机性改变探索策略, Plappert等人^[8]提出在参数空间加入适当的噪声; Fortunato等人^[9]提出在参数空间与动作空间加入噪声相结合的方法. 不同于非盲目式的改变探索策略, Bellemare等人^[10]将对状态的虚拟计数作为衡量不确定性的指标; Pathak等人^[11]提出基于好奇心驱动的探索方法记录对状态的访问次数, 用于赋予内在奖励以鼓励智能体探索; 杨珉等人^[12]使用贝叶斯线性回归方法提高智能体的探索效率; 李超等人^[13]根据智能体对于状态空间的离散化程度改写值函数形式, 基于该值函数对环境进行合理探索. 当然, 若能够有效构建环境模型, 智能体将无需再与环境进行真实的交互, 直接从拟合的环境模型中获取数据样本. Tangkaratt等人^[14]提出学习控制的概率推理方法使用高斯过程对状态转移模型进行建模, 使用最小二乘条件密度来学习状态转移模型; Ha等人^[15]构建神经网络生成模型, 学习低维空间下的状态表示的世界模型. 这些方法都是通过从智能体与环境交互的角度出发来提升样本效率, 忽略了如何在本身已获得的数据样本上, 减少智能体与环境的交互次数. 因而, 在从与环境的交互中获取数据样本后, 如何高效利用样本也会影响到样本效率. Schaul等人^[16]提出优先经验回放算法通过TD-error值赋予状态转移样本不同的重要性; 赵英男等人^[17]提出先以序列累计回报作为样本优先级再以TD-error分布构造优先级的二次采样的方式对样本进行选择; 朱斐等人^[18]通过奖赏、时间步和采样次数共同决定样本的优先级, 使智能体能更有效的选择动作; Lin等人^[19]提出的序列记忆深度Q网络算法通过存储经验的奖赏值对采样到的状态转移样本进行区别对待等. 但以上的采样方式都是单个看待经验回放单元中的状态转移样本, 由于强化学习中的奖励具有稀疏性与延迟性, 对单个样本进行采样时很容易采样到不具有奖励的状态转移样本, 导致采样效率低. 同时, 强化学习作为一种通过与环境交互、从环境状态到动作映射的学习方式, 在学习过程中会产生无数条序列轨迹, 这些序列轨迹由多个样本所组成, 并且每个序列样本都会带有奖赏值. Lee等人^[20]在2019年提出的序列向后更新(Episodic Backward Update, EBU)算法, 不同于以往对状态转移样本进行单个采样的方式, 通过采样整个序列轨迹由后向前更新对深度Q网络进行训练, 更快地传播奖赏值, 提高了采样效率.

遗传算法作为求解最优问题的常用算法, 能通过模拟生物在自然环境中的进化过程搜索全局最优解. 其中交叉操作能采用多种交叉方法以生成新的个体^[21]. 当面临深度强化学习中需要解决减少智能体与环境的交互次数的问题时, 运用能产生新个体的交叉算子, 进而对数据样本数量进行扩充. 因此, 本文尝试利用遗传算法中的交叉算子, 作用于序列轨迹以产生新的序列样本, 从而扩充序列样本数量, 减小智能体与环境的交互次数, 使智能体能获得更优策略. 在Playing Atari 2600视频游戏验证本方法, 实验结果显示该方法能获得更高的平均奖赏值并提高样本的利用率.

1 研究基础 1.1 强化学习

在强化学习中, 智能体通过与环境进行交互以达到最大化累计奖赏的目标, 整个学习过程使用马尔科夫决策过程进行建模: 在每个离散的时间步 $t$ , 智能体从与环境的交互过程中获得状态的表示 ${s_t}$ , 依据当前策略 $\pi $ , 得到应采取的动作 ${a_t}$ , 执行该动作得到即时奖励 ${r_t}$ 并转移到下一状态 ${s_{t + 1}}$ . 这个过程一直循环下去, 直到到达标志着智能体的任务结束时的终止状态, 意味着完成一个序列轨迹. 状态转移样本表示为 $({s_t},{a_t},{r_t},{s_{t + 1}})$ , 智能体从初始状态到终止状态的序列轨迹由状态转移样本构成, 表示为: $({s_1},{a_1},{r_1},{s_2}),\cdots,({s_t},{a_t},{r_t},{s_{t + 1}})$ .

智能体在一个序列中状态 ${s_t}$ 所获累计奖赏值定义为:

${G_t} = \sum\limits_{k = 0}^T {{\gamma ^k}} {R_{t + k + 1}}$

(1)

其中, 折扣因子 $\gamma \in (0,1]$ 用于调节不同状态对累计奖赏值的影响程度. 强化学习的目的是学习到使得 ${G_t}$ 期望值最大的策略, 动作值函数定义为:

$ \begin{split} {Q}_{\pi }(s,a)&={E}_{\pi }[{G}_{t}|{S}_{t}=s,{A}_{t}=a]\\ &={\displaystyle \sum _{{s}^{\prime }\in S, {a}^{\prime }\in A}p({s}^{\prime }|s,a)}[r+\gamma {Q}_{\pi }({s}^{\prime },{a}^{\prime })]\end{split}$

(2)

由于状态转移概率未知, 可通过Q学习更新值函数:

$ Q(s,a) \leftarrow Q(s,a) + \alpha [r + \gamma \mathop {\max }\limits_{a' \in A} Q(s',a') - Q(s,a)] $

(3)

经过式(3)的不断迭代, 最终状态值函数 $Q(s,a)$ 会收敛到最优值, 达到最大化累计序列奖赏值的目标.

1.2 深度强化学习与经验回放

在强化学习面对高维状态空间时, 深度Q网络^[1]算法通过引入深度学习中的神经网络对Q学习算法中的Q值进行参数化, 经验回放机制为神经网络的训练提供数据样本. 经验回放单元D存储了智能体在每个时间步生成的状态转移样本 $({s_t},{a_t},{r_t},{s_{t + 1}})$ , 此时, 状态动作值函数更新方式为:

$ Q(s,a;\theta ) \leftarrow Q(s,a;\theta ) + \alpha [r + \gamma \mathop {\max }\limits_{a' \in A} Q(s',a';\theta ') - Q(s,a;\theta )] $

(4)

训练过程中, 智能体从经验回放单元中随机选择状态转移样本执行更新, 利用随机梯度下降方法最小化损失函数:

$L(\theta ) = {E_{(s,a,r,s') \sim D}}\left[ {{{(y - Q(s,a;\theta ))}^2}} \right] $

(5)

其中,

$ y = \left\{ {\begin{array}{*{20}{l}} {r + \gamma \mathop {\max }\limits_{a' \in A} Q\left( {s',a';\theta '} \right), \;如果s'是终态}\\ {r, \qquad \qquad \qquad \quad \quad\; 否则} \end{array}} \right. $

(6)

式(6)中, $\theta '$ 为目标值函数网络的参数, 在一定的周期内将当前网络参数复制给目标值函数网络, 以保证学习过程的稳定性.

1.3 EBU算法

EBU算法的主要工作是解决深度强化学习中的样本效率问题. 主要有以下两方面:

(1) 深度Q网络通过均匀随机选择的方式对状态转移样本进行采样, 但在许多问题中, 智能体与环境交互所获的奖励往往具有稀疏性与延迟性, 该方式会使得抽样到具有奖励的状态转移样本的概率很低. (2) 在训练早期阶段, 所有Q值初始化为0, 在使用式(4)对Q值进行更新时, 若下一状态的Q值也为0, 会导致更新所获信息无效. 因此, 该算法通过采样一整个序列样本进行训练, 能保证至少一个带有奖励的状态转移样本被采样到, 同时, 在对Q值进行更新的时候, 从序列末尾往序列开始的方向进行更新, 使得更新过程能充分利用有效信息^[11].

具体训练过程中, 采样一整个序列样本后, 通过序列由后向前更新的方式赋予式(6)中的y值. 由于直接使用此y值会造成深度Q网络的不稳定问题, 通过引入调节因子 $\;\beta $ 降低影响, 更新方式为:

$\tilde Q[{A_{k + 1}},k] \leftarrow \beta {y_{k + 1}} + (1 - \beta )\tilde Q[{A_{k + 1}},k]$

(7)

其中, $k$ 为序列时间步, $\tilde Q$ 值为从目标值函数网络中获取的值. 当 $\;\beta {\rm{ = }}0$ 时, 相当于一步更新的深度Q网络; 当 $\;\beta {\rm{ = }}1$ 时, 容易产生过估计问题. 该算法分为固定 $\;\beta $ 值和自适应 $\;\beta $ 值两种, 本文仅针对样本问题, 选取固定 $\;\beta $ 值的算法进行研究.

2 基于遗传交叉算子增强深度Q网络 2.1 利用交叉算子扩充序列样本数量

强化学习作为基于行为的学习方式, 不同于依据正例与反例来告知应采取何种行为的监督与非监督学习, 需要通过试错的决策过程来生成无数条序列轨迹, 以用来发现最优策略. 为了减少该决策过程所需消耗的成本与代价, 可采用遗传交叉算子对序列轨迹进行扩充. 强化学习试错的学习方式会使得序列轨迹中存在相似状态, 选择这些相似状态作为交叉点, 能产生出目前未出现过的序列轨迹, 以此用来扩充序列轨迹数量, 提高对当前样本的利用率.

本文将智能体与环境交互产生的序列样本作为染色体, 序列样本中的状态作为基因. 每次从经验回放单元中选择两条染色体作为父代, 选取相似基因作为交叉点, 采用遗传算法中的单点交叉算子, 交换父代基因生成两个子代. 具体而言, 可如图1所示, 经验回放单元可表示为 $D = \{ {e^1},{e^2}, \cdots \} $ , ${e^i} = \{ (s_1^i,a_1^i,r_1^i,s_2^i),(s_2^i,a_2^i,r_2^i,s_3^i), \cdots , $ $ (s_{T-1}^i,a_{T-1}^i,r_{T-1}^i,s_T^i)\} $ 为经验回放中的第i个序列, 在D中选择两个序列 $ {e}^{i}、{e}^{j}$ , 判定 $s_3^i$ 与 $s_4^j$ 作为交叉点, 依据单点交叉生成新的 ${e^{i'}}$ 与 ${e^{j'}}$ 并存入D'中.

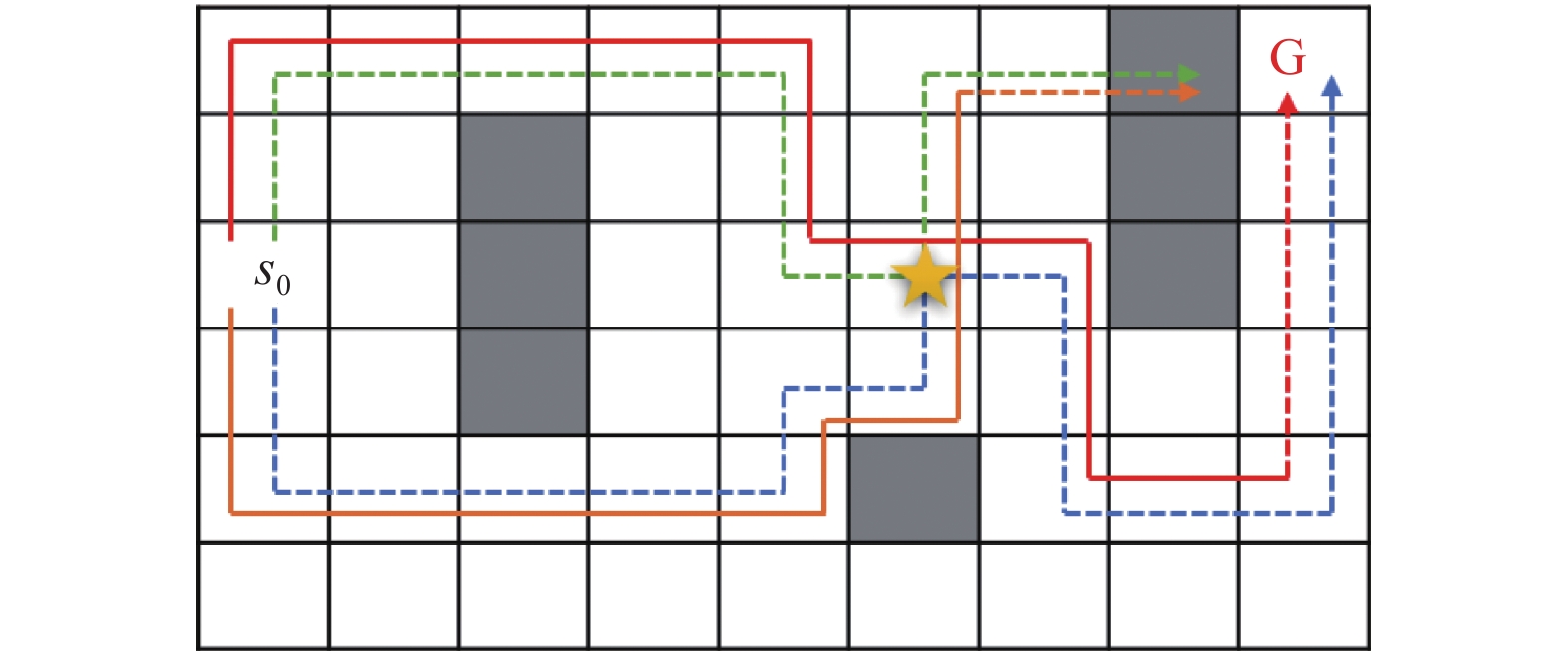
同时, 由于经验回放单元中所存储的序列是由智能体不断与环境交互试错生成, 因此每条序列的终态会存在大量相似性, 在选择序列进行交叉操作时, 我们所选取的应是以不同状态作为终态的序列轨迹, 以便利用遗传算子的探索能力, 增加新生成的序列的多样性. 如图2所示, 在这个迷宫环境中, 绿色与蓝色轨迹是智能体与环境交互生成, 且以不同的状态作为结尾, 黄色五角星为交叉状态所在的位置, 红色与橙色为交叉后生成的序列轨迹. 若选择以相同状态作为结尾的轨迹, 虽然也能产生新的序列, 但并没有选择以不同状态作为结束的轨迹交叉而产生的序列轨迹的多样性高.

此外, 由式(1)计算每条序列的累计奖赏, 其可作为当前策略的评价指标, 累计奖赏值越大说明当前策略越优. 并且, 序列累计奖赏值越大的序列所包含的有效动作样本越多^[15], 意味着使用这些状态转移样本会更有利于学习最优策略. 因此, 对于利用交叉算子所生成的新序列, 我们仅保留序列累计奖赏变高的序列. 通过使用交叉算子生成的序列降低了数据样本的生成成本, 增加了经验回放单元中的序列数量.

2.2 判定状态相似的方法

当状态空间巨大甚至无穷时, 一个状态出现在两个不同的序列轨迹中的概率非常低. 交叉点不必是两个不同序列中的完全相同的状态, 而是两个相似度高的状态. 是因为强化学习采用函数近似之后, 本质上就是对有限样本上的经验进行泛化, 把所访问过的状态的值推广到新的近似状态上.

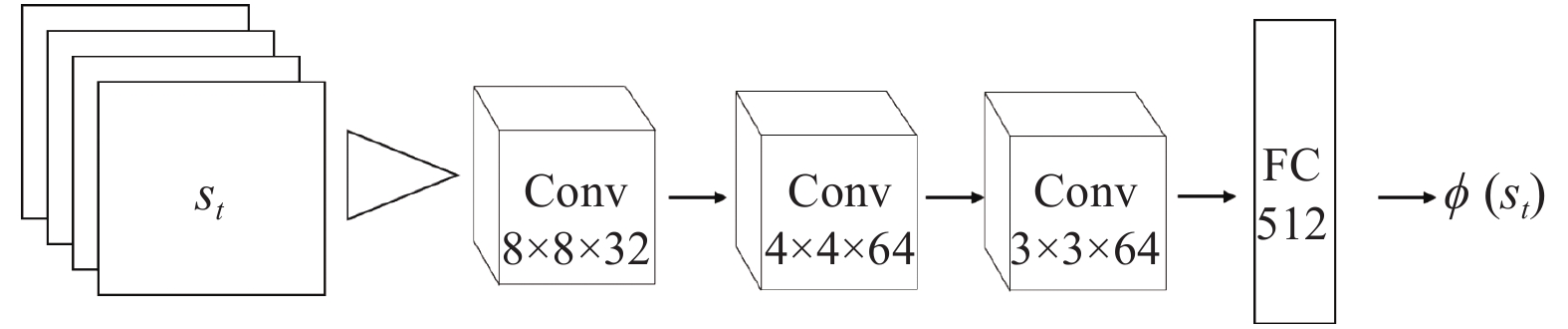
深度Q网络中采用直接将图像作为输入, 通过深度神经网络提取出高层特征, 实现端到端的训练方式. 基于神经网络提取的高层特征度量两个状态的相似度一方面降低了维度, 另一方面也抓住了所求解问题的状态内在相似的内在本质. 这里, 用于特征提取的深度神经网络结构如图3所示.

对序列轨迹中的状态进行高层特征抽取后, 比较两状态特征之间的距离, 距离越大说明相似度越低, 距离越小则相似度越高. 依据式(8)计算特征之间的距离:

$d\left( {s_t^i,s_t^{{j}}} \right) = \sqrt {{{\left( {\phi \left( {s_t^i} \right){\rm{ - }}\phi \left( {s_t^{{j}}} \right)} \right)}^2}} $

(8)

其中, $\phi (s_t^{})$ 为通过深度神经网络对状态进行特征抽取后的结果.

2.3 从经验回放单元中选择样本

强化学习作为利用试错的方法解决序贯决策问题的学习方式, 每条序列轨迹都是智能体为了达到最终的学习目标所做出的尝试, 经验回放单元中存储着智能体与环境实时交互所产生的序列轨迹. 与序列向后更新算法类似, 我们通过选择整个序列的采样技术, 使得深度Q网络在训练时采取从整个序列由后往前的状态转移样本进行训练.

通过使用对原始经验回放单元中的序列轨迹进行交叉操作后, 将交叉生成的新的序列轨迹存储在经验回放单元D'之中, 得到了新的经验回放单元D'. D'作为原始经验回放单元D的补充, 在采样过程中, 优先采样D中的序列, 再以一定的概率采样新的经验回放单元D'中的序列, 具体为随机产生[0, 1]之间的随机数 $\sigma $ , 如果小于设置的参数 $\;\mu $ , 则从经验回放单元D中选择序列样本, 反之, 从D'中选择.

2.4 算法描述

本文提出的利用遗传交叉算子(Genetic Crossover Operator, GCO)扩充序列样本的方法是建立在序列向后更新(EBU)算法的基础上, 为智能体在选择序列样本进行训练时, 扩大序列样本的选择面, 增大序列样本多样性, 有利于获得更优质的策略. 具体算法如算法1.

算法1. GCO-EBU算法

1) 初始化: 记忆回放单元D的容量为N, 生成的记忆回放单元D'容量为N', 折扣因子γ, 学习率η, 抽样样本批量大小B, 训练最大时间步M, 目标Q网络更新频率F;

2) fore=1 toIdo:

3) fort=1 to $\scriptstyle {T_e}$ do:

4)     基于当前状态 $\scriptstyle {s_t}$ , 以 $\scriptstyle \varepsilon $ 的概率随机选择动作 $\scriptstyle {a_t}$ , 否则选择动作 $\scriptstyle {a_t} = \mathop {\arg \max } Q(s,a;\theta )$ ;

5)     执行动作 $\scriptstyle {a_t}$ 并观察到下一状态 $\scriptstyle {s_{t + 1}}$ , 获得即时奖励 $\scriptstyle {r_t}$ , 以及是否达到终态;

6)     获得状态转移样本 $\scriptstyle ({s_t},{a_t},{r_t},{s_{t + 1}})$ , 存储到经验回放单元D中;

7)     利用式(8)从D或D'中采样序列e', 采样到的序列长度为L;

8)     初始化临时目标Q表 $\scriptstyle \tilde Q = \tilde Q(s', \cdot ;\theta ')$ ;

9)     初始化目标向量y, $\scriptstyle {y_L} = {R_L}$ ;

10) for $\scriptstyle k = {T_{e'}} - 1$ to 1 do:

11)     $\scriptstyle \tilde Q[{A_{k + 1}},k] \leftarrow \beta {y_{k + 1}} + (1 - \beta )\tilde Q[{A_{k + 1}},k]$

12)     $\scriptstyle {y_k} \leftarrow {R_k} + \gamma {\max _{a \in A}}Q[a,k]$

13) end for

14)  计算损失函数 $\scriptstyle L(\theta ) = {\left( {y - Q(s,a;\theta )} \right)^2}$ ,并由梯度下降更新参数 $\scriptstyle \theta $ ;

15) if $\scriptstyle t{\text{%}} F$ ==0:

16)       $\scriptstyle \theta ' = \theta $

17) end for

18)   从经验回放中选择以不同状态作为终态结束的序列 $\scriptstyle {e^i}$ , $\scriptstyle {e^j}$

             $\scriptstyle {e^i} = < s_0^i,a_0^i,r_0^i,s_1^i,a_1^i,r_1^i,s_2^i, \cdots ,s_{{T_i}}^i >$

             $\scriptstyle {e^j} = < s_0^j,a_0^j,r_0^j,s_1^j,a_1^j,r_1^j,s_2^j, \cdots ,s_{{T_j}}^j > $

19) 选取序列eⁱ, e^j中 $\scriptstyle d(s_m^i,s_n^j)$ 最小的两个状态作为交叉点

20) 应用交叉算子生成新的序列样本

　　　 $ \scriptstyle {e}^{{j}^{\prime }}=<{s}_{0}^{j},{a}_{0}^{j},{r}_{0}^{j},{s}_{1}^{j}, \cdots ,{s}_{m}^{i},{a}_{m}^{i},\cdots ,{s}_{{T}_{i}}^{i}>$

　　　 $\scriptstyle {e^{i'}} = < s_0^i,a_0^i,r_0^i,s_1^i, \cdots ,s_n^j,a_n^j, \cdots ,s_{{T_j}}^j > $

21) 将 $ \scriptstyle {e}^{{i}^{\prime }}、{e}^{{j}^{\prime }}$ 存入 $\scriptstyle D'$

22) end for

该算法中, 4)–6)步为强化学习使用ε-greedy策略作为行为策略产生样本, 并将样本保存到经验回放单元中; 7)–16)步是采样序列样本并进行训练的过程, 其中7)–12)步为EBU算法过程, 通过从后向前倒序回放序列中的状态转移样本进行训练, 第7)步为控制采样到本文所提出方法所生成的序列样本的比例; 18)~20)步是通过交叉操作产生新的序列的过程, 从经验回放单元中随机选择到两条序列, 比较两条序列的终态的高级特征是否相似, 选取终态差异较大的序列进行交叉, 其中第19)步为依据状态的高级特征判断出两条序列的交叉点, 依据交叉点最终完成交叉, 生成出新的序列样本.

3 实验分析 3.1 实验设置

本文采用ALE作为实验验证平台. ALE中包含了大量各种类别的Playing Atari 2600游戏接口, 为研究深度强化学习提供了丰富内容, 许多改进的深度强化学习算法都在该平台验证. 采用Playing Atari 2600游戏中的9个控制问题验证本文方法的有效性, 控制问题分别为Breakout、Space_invaders、Ms_pacman、Atlantis、Phoenix、Video_pinball、Assault、Asteriods.

将本文方法与NATURE-DQN^[1]、EBU^[20]算法进行对比, 其中NATURE-DQN的训练过程是从经验回放单元中随机选择样本, 本文则是在利用序列样本训练的EBU算法基础上应用所提出的方法. 具体参数设置为: 由于ALE所提供的游戏画面大小统一为210×210, 为了方便训练, 将图像灰度化处理并将大小裁剪为84×84, 并将4帧图像作为一个状态看待; 由于每个Atari游戏奖励设置不同, 实验过程中对每个游戏所获的奖励进行统一化处理, 即将奖励归一化在[−1,1]之间; 在训练过程中, 经验回放单元初始化是没有任何样本存在, 两个经验回放单元大小设置为1000000, 在智能体与环境交互超过50000步时再从经验回放单元中选择样本进行训练, 每次选择样本的个数为32的倍数, 序列样本的大小不足32的倍数时, 在往前选择状态转移样本进行填充; 使用ε-greedy策略作为智能体的行为策略, $\varepsilon $ 大小随着步数从1递减到0.1; 采用RMSProp方式更新网络参数, 动量设置为0.95; 折扣因子 $\gamma $ 设置为0.99; 学习率设置为0.00025; 选择经验回放单元D'的参数 $\;\mu $ 设置为0.9; 网络结构与N3ATURE-DQN相同, 使用三层卷积网络与两层全连接网络构成, 第1层卷积具有32个大小为8×8的滤波器, 步长为4, 第2层卷积具有64个大小为4×4的滤波器, 步长为2, 第3层卷积具有64个大小为3×3的滤波器, 步长为1, 选取的激活函数为ReLU, 第1层全连接具有512个神经元, 第2层全连接神经元个数为当前游戏所对应的动作空间大小; 目标值网络与该网络结构相同, 每隔10000步将当前网络参数赋给目标值网络. 在对序列样本进行交叉操作时, 使用三层卷积层与一层全连接层对状态进行高层特征抽取, 判断两个状态是否相似. 本文采用的EBU算法为文献[20]中的算法2, 超参数 $\;\beta $ 为0.5.

3.2 实验结果与分析

在实验中, 3种方法均采用相同的实验参数, 图4为实验结果曲线图, 横坐标为epoch, 每个epoch包含62500步, 即智能体与环境交互62500次, 纵坐标为各方法中智能体结束一个epoch后测试30次序列的平均累计奖赏值, 奖赏值越高说明智能体所学习到的策略越优.

通过实验结果可以看出, 本文提出的方法GCO-EBU与NATURE-DQN和EBU算法相比, 在多数控制问题上能使用更少的与环境交互的次数获得更高的奖赏值. 具体而言, 在图4(a)–图4(d)的Assault、Space_invader、Altantis、Phoenix控制问题上GCO-EBU算法能在训练初期就能观察到明显效果, 说明相对于两个对比算法, 我们对序列样本数量的扩充为训练提供了帮助, 使得智能体获得了更高的平均奖赏值. 在图4(e)Asteroids问题中, GCO-EBU在训练初期效果低于对比算法, 但在训练后期所获奖赏值远高于两种方法,由于该问题在训练初期序列轨迹终态相似度高, 利用交叉所生成的轨迹并未给序列样本好的扩充, 而在训练后期终态相似度大, 能生成出多样性大的序列轨迹. 在图4(f)–图4(g) Breakout、Video_pinball问题上, 所获奖赏值的曲线比较相似, 稳定性低于其他问题, 这和两个问题的游戏规则有关. Breakout问题上GCO-EBU优于NATURE-DQN算法, 但和EBU算法相比却没有更大的改进, 这由于Breakout问题在游戏初期所获的奖赏值是非常稀疏的, 导致在运用本文方法时, 所生成的序列样本的累计奖赏值发生改变的情况过少, 因此未能达到很好扩充序列样本的目的. 由Video_pinball问题的实验结果图也可看出, GCO-EBU与EBU相比的效果也并不明显, 但整体而言, 本文所提出的方法还是能帮助智能体在相同时间内获得更高的奖赏值. 在图4(h) Ms_pacman问题上, GCO-EBU与EBU的实验效果不如NATURE-DQN, 但本文的改进是建立在EBU算法上, 在训练后期本文方法在相同的与智能体交互次数中所取得的奖赏值高于EBU.

表1是3种算法在8个控制问题上的平均奖赏值的对比, 整体而言, 说明依据遗传算子来扩大序列样本数量, 增加序列样本多样性的方法, 能使得在智能体与环境的相同交互次数中, 探索到更多的序列, 提高样本的利用率, 从而获得更高的奖赏值, 得到更优质的策略.

4 结论与展望

本文所提出的利用遗传算法中的交叉算子作用于序列样本的方法, 能增大深度强化学习算法的序列样本数量, 减少智能体与环境的交互次数, 提升样本效率, 使得智能体获得更高的平均奖赏值, 最终导出更优质策略. 通过ALE平台上的8个Playing Atari游戏验证了该方法的有效性. 目前仅在基于值函数的强化学习算法上验证本方法, 今后的研究工作是将该方法应用于基于策略的强化学习算法, 通过扩充序列样本的方式, 增大策略空间, 更好地服务于策略梯度算法, 使得策略能跳出局部最优的困境.