2. 中国航天员科研训练中心, 北京 100094
2. Scientific Research Training Center for Chinese Astronauts, Beijing 100094, China
传统睡眠监测手段会对人体正常睡眠造成一定程度的干扰, 其睡眠数据的客观性和真实性也相应受到影响, 难以满足家庭睡眠监测的实际应用需求, 非接触方式实现的睡眠监测系统则可以克服传统睡眠监测设备中的弊端.床垫式睡眠监测系统通过在床垫中安装压力或压电传感器, 可以对人体呼吸和心跳等典型生理特征参数进行无扰式监测, 因其具有使用简单的优点, 其相关理论研究已成为生理信号监测领域的热点问题[1-4].
基于压电薄膜传感器的床垫式睡眠监测系统可以感知微小压力或震动变化, 从而捕获心冲击(BCG)力传至体表的震动成分、呼吸时人体胸腔起伏对床垫的压力变化以及体动等信息并转为电信号. 但由于采用该方式采集的信号是集呼吸、心跳以及噪声等在内的复杂生理信号, 需要从混合信号中实现呼吸和心跳等信号的有效分离和识别, 才能准确计算呼吸率和心率等关键睡眠特征参数.
对心冲击信号进行分离和提取时, 大多采用常规的滤波器、小波变换或经验模态分解(EMD)等方法实现[5-8]. 常规的滤波器无法准确描述其局部特性, 且常规滤波器需要根据先验知识预定义滤波器截止频率, 无法根据心率的变化动态分割频谱; 若采用小波变换, 因难以选取合适的小波基和分解层数, 且缺乏自适应性, 故信号提取效果不佳; EMD方法则存在模态混叠, 缺乏完备理论基础以及计算量大等局限[9]. 本文采用基于经验小波变换(Empirical Wavelet Transform, EWT)的信号处理方法, 可以根据原始信号特点, 动态地确定呼吸和心跳等信号的频带范围, 对输入信号进行自适应分解和重构, 有效提取呼吸和心冲击信号. 在此基础上, 采用K-means聚类算法进行心跳定位.
1 床垫式生理信号监测系统本设计所采用的睡眠监测系统方案如图1所示, 睡眠监测系统主要由传感器装置、监测系统主机以及监测终端设备3部分构成. 本设计采用基于压电薄膜传感器的监测床垫进行信号采集, 并设计了具备电荷放大、滤波以及信号放大等功能的信号调理电路. 经调理后的电压信号送至低功耗单片机进行AD转换, 转换后的结果通过WiFi模块送至监测终端进行后续算法处理和数据分析.

|
图 1 监测系统框图 |
1.1 传感器装置
睡眠状态下人体心脏跳动、正常的呼吸均会使产生一定幅度的震动, 并导致床垫上有轻微的压力波动.与其他运动相比, 心跳所产生的压力变化微弱, 且容易淹没在呼吸和环境噪声中, 故其提取最为困难. 因此传感器选择优先考虑满足心跳信息提取要求, 并兼顾适合床垫式监测的需求.
考虑到聚偏二氟乙烯(PolyVinyliDene Fluoride, PVDF)压电薄膜传感器不仅具有灵敏度高、可精确测量动态压力的优点[10], 而且可实现最低0.1 Hz的检测频率, 可在本系统中实现动态压力检测. 在实际监测装置中将包含传感器的带状物放置在床垫与被褥之间, 该传感器可通过感知床垫上压力的变化产生与人体心跳、呼吸以及体动等信息相关的混合信号输出.
1.2 控制器主机监测系统主机主要由包含STM32F405高性能处理器的生理信号实时采集和传输模块构成. 采集模块中传感器信号调理电路等效电路如图2所示.

|
图 2 电荷输入信号调理电路 |
在该等效电路中, Ca与Ra为传感器的等效电容和绝缘电阻; Cc为传输电缆等效电容; Ri与Ci为放大器输入电阻和输入电容; Rf与Cf为放大器的反馈电阻和反馈电容; Q为传感器产生的电荷输出. 在忽略Ra、Ri与Rf的影响时, 电荷放大电路产生的电压输出Uo为:
| ${U_{{o}}} = - KQ/\left[ {{C_{{i}}} + {C_{{c}}} + {C_{{a}}} + \left( {1 + K} \right){C_{{f}}}} \right]$ | (1) |
式中, K为运放开环增益, (1+K)Cf为密勒电容, 由于K通常很大, 故Uo表达式可简化为:
| $ {U_{{o}}} = - Q/{C_{{f}}} $ | (2) |
由式(2)可知, Uo仅与电荷量Q以及反馈电容Cf有关, 电缆长度对其影响可忽略不计. 由于运放工作在深度电容负反馈状态, 对于直流工作点而言相当于开环, 容易受到各种噪声的影响导致较大的零点漂移, 从而产生幅度较大的干扰信号输出. 为了使放大器工作稳定并减小零漂, 可在Cf两端并联阻值较高的反馈电阻Rf, 起到提供直流负反馈且有利于稳定放大器直流工作点的作用.
本系统所设计调理电路如图3所示. 在该电路中反馈电阻R1和反馈电容C1的选择非常关键. 考虑到要呼吸信号特征频率集中在1 Hz以下, 要使电荷放大电路具有良好的低频响应能力, 要求低频转折频率fCL应尽可能低, 而fCL可由式(3)得到:
| $ {f_{{\rm{CL}}}} = 1/\left( {2{\text{π}} {R_{\rm{1}}}{C_{\rm{1}}}} \right) $ | (3) |
由式(3)可知, 从放大有用信号的角度来考虑, 应使C1取值尽可能大, 但过度增加电容取值又会造成传感器灵敏度下降, 使得有效信号混杂在噪声中, 不利于后续滤波电路处理. 因此, 要根据实际应用选取合适的反馈电容数值. 反馈电阻取值越大则放电时间常数越大, 电路具备良好的低频响应能力; 但是取值过高又会使得输入偏置电流产生饱和的偏压输出, 从而导致无法获取有用的信号输出. 经试验比对和分析, 最终选择反馈电阻和反馈电容的取值分别为100 MΩ和20 nF, 故对应的fCL为0.079 Hz.

|
图 3 PVDF传感器和Q/V转换电路等效电路 |
微处理器采集数据后通过串口WIFI模块定时发送至监控终端, 监控终端接收到数据后, 进行分析处理. 设计出的监测系统主机如图4所示.

|
图 4 睡眠监测主机 |
2 信号处理方法 2.1 经验小波变换
EWT是一种快速且完全自适应的小波技术, 其理论基础是自适应模态分解与小波分析理论[11]. EWT变换的目的是分离不同频谱的信号分量. 本设计采用极大极小值法进行自适应频谱分割: 将傅立叶谱归一化至[0,π]之间, 并用N+1个边界将其分成N段. 由于傅立叶谱在[0,π]之间, 故需要再确定N−1个边界, 可首先检测频谱中的极大值, 然后选取每两个相邻极大值之间的全局最小值定义为边界集. 假设该算法找到了M个最大值, 则可能出现两种情况:
(1) M ≥ N: 该算法找到足够的极大值来定义所需的段数, 此时仅保留前N−1个极大值;
(2) M < N: 信号模式比预期少, 保留所有极大值并将N重置为合适值.
频谱分割后即可根据选取的边界点构建小波带通滤波器组提取不同的模态分量IMF, 从而分离出心跳和呼吸.
2.2 心跳定位及心率计算方法提取出BCG信号后, 还需进行心跳定位计算心率. 心脏收缩和舒张过程中, 泵血冲击力变化会使得信号在每个心脏跳动周期内形成如图5所示的多种波峰模式[12]. J波作为幅值特征最为明显的波峰, 常作为心跳定位的重要标志. 实际分离得到的BCG信号中, 存在同类波峰的峰值差别较大而不同类波峰峰值却比较相近的情况, 故不能单纯依靠波峰峰值来进行分类. 为使系统能自动检测与单个心跳相对应的BCG波峰模式, 需根据波峰模式的形态学特征建立特征向量, 选用无监督的K-means聚类算法对BCG信号极大值点进行聚类, 选出平均幅值最大的波峰作为J波波峰并用于确定心跳位置. 根据定位结果可计算平均心跳周期和心率. 心跳定位具体步骤如下:

|
图 5 典型BCG信号波峰模式 |
(1)建立特征工程. 如图6所示, 对BCG信号中极大极小值点进行定位和参数化, 4个基本参数包括当前极大值点幅值amax、下一极小值点幅值amin、当前极大值点到相邻极小值点距离dmax以及下一极小值点到相邻极大值点距离dmin. 为BCG信号中每个波峰分配特征向量f, 该向量包含波峰本身和N−1个连续峰的基本参数. 此处将N设置为4, 故须建立一组16维的特征向量.

|
图 6 BCG波峰模式特征向量示意图 |
(2)聚类. 对于给定欧氏空间的一组数据, 寻找K个聚类中心, 将所有数据分配到距离最近的聚类中心, 使得每个点与其相应的聚类中心Cj距离平方和最小, 从而将波峰分为K类.
(3)判断J波位置. 对每类极大值点计算幅值的平均值, 选取平均值最大的一类作为识别的J波类. 此时J波位置即为心跳位置.
(4)计算心跳平均周期及心率. 对每个心跳周期大小进行排序, 取序列中间60%的心跳周期计算平均值, 进而计算心率.
3 实验分析 3.1 呼吸信号和BCG信号提取图7是利用所设计的监测主机获得的30 s归一化采样信号. 对其工频滤波预处理后, 利用极大极小值法进行频谱划分.

|
图 7 原始采样信号归一化图 |
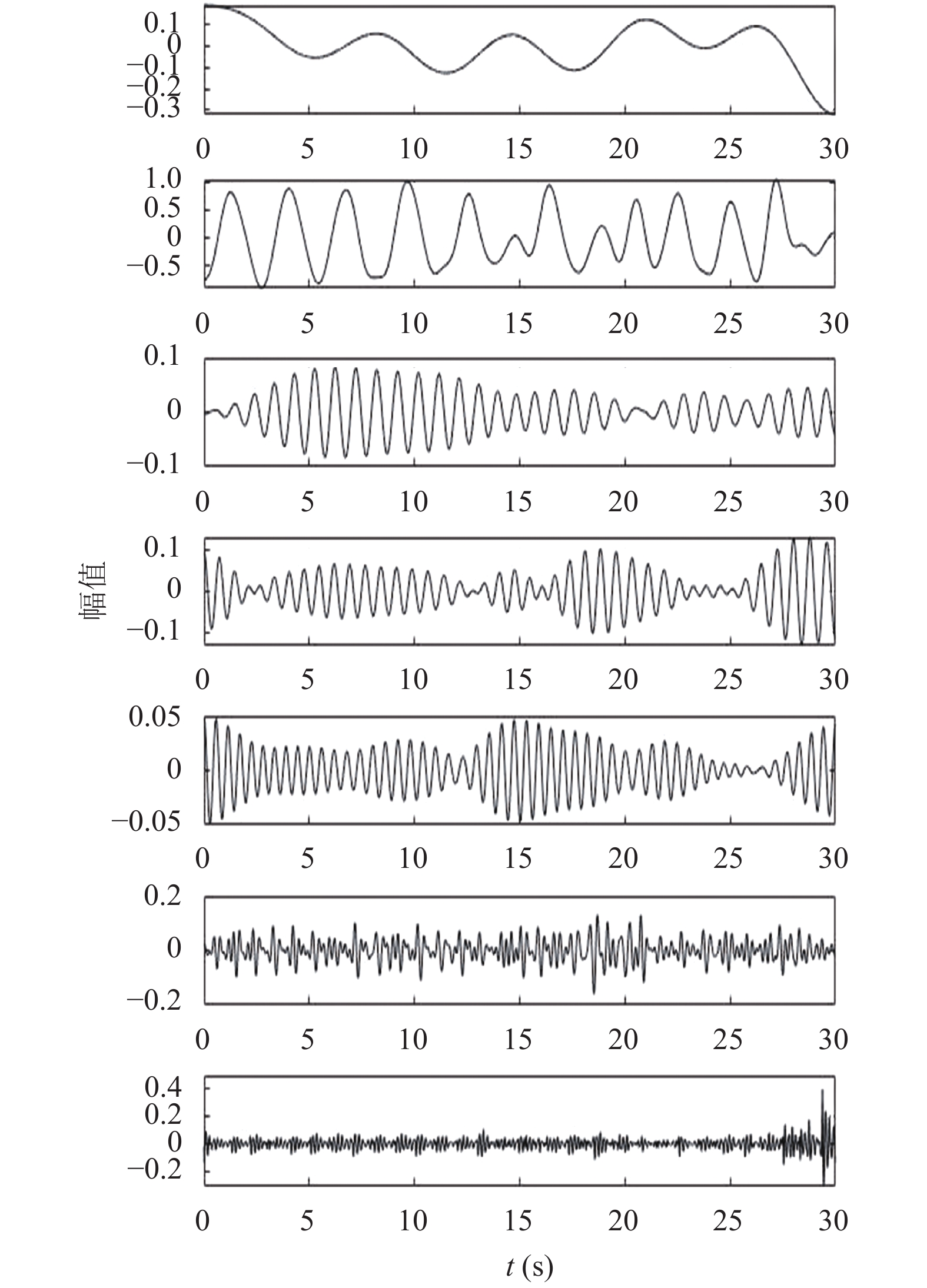
EWT具有很强自适应性, 根据原始信号的频域分布特点, 当选择单分量数目为7时, 可避免频带过度划分, 所提取的呼吸和心冲击信号波形形态特征比较符合实际, 提取效果较好. 对原始信号进行EWT分解的频带边界分割效果如图8所示, 与之相对应的各模态分量对应时域波形如图9所示. 从呼吸和BCG信号的波形特点来看, 第二个模式分量具有明显周期性, 符合理想呼吸信号特征; 第6个分量波峰模式清晰可辨, 同时具备较强周期性, 与理想BCG信号波形效果基本一致.

|
图 8 边界划分结果 |
|
图 9 EWT分解信号 |
3.2 心跳定位和心率计算
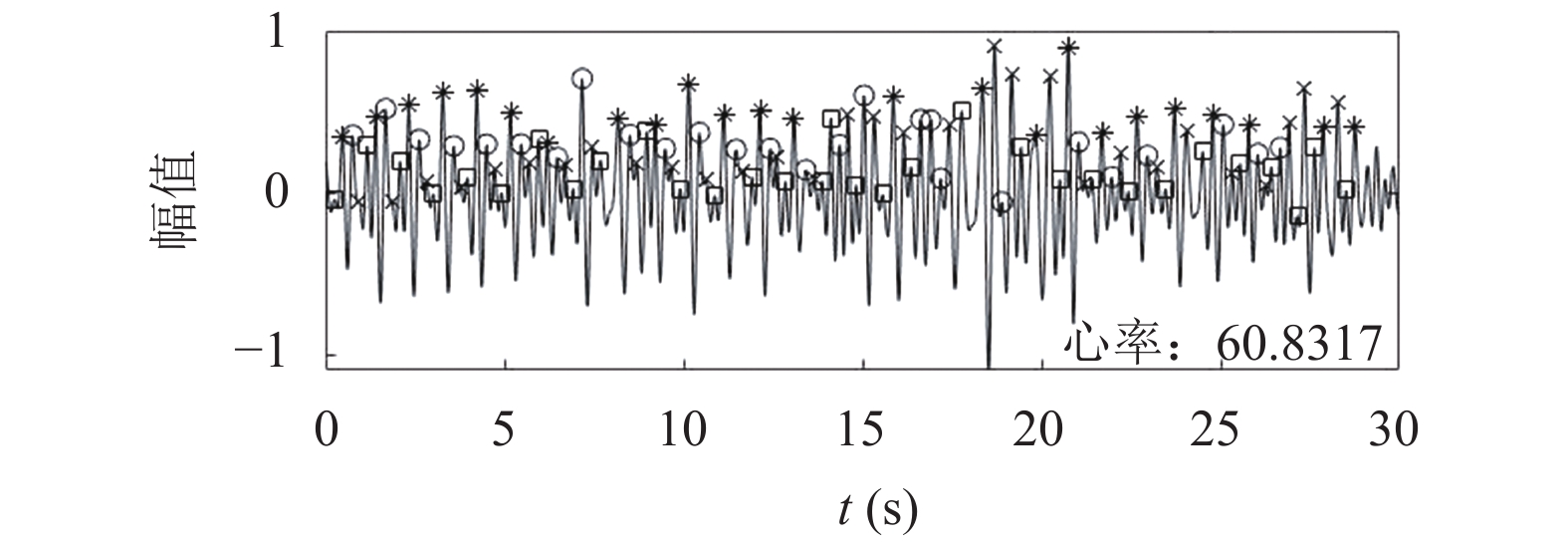
对提取的BCG信号做归一化处理, 然后对信号内极大值点建立特征向量序列, 利用K-means算法对极大值点进行聚类. 考虑到心冲击信号在心跳周期内包含4种波峰模式, 故选择将波峰分为4类. 聚类结果如图10所示, 图中用不同符号对不同类型波峰模式进行区分.
|
图 10 特征点分类标记波形图 |
实验结果表明, 采用K-means方法处理的BCG信号无需预先估计心跳周期即可较为准确地完成心跳定位, 从整体来看聚类效果良好, 周期规律比较明显, 心率计算结果符合正常睡眠心率.
4 结论与展望基于PVDF压电薄膜传感器和高性能微处理器STM32F405, 研制出一套睡眠监测装置, 并采用经验小波变换和K-means算法相结合的方式实现了对混合信号的分离以及典型生理特征参数的有效提取. 该信号处理方法克服了传统BCG信号处理中需要预先估计心跳周期大致范围或需要人工标记才能进行实验的局限, 且具有较强的自适应性.
| [1] |
郭健, 陈雨行, 王丽荣, 等. 非接触式呼吸与心率信号采集系统. 光学 精密工程, 2019, 27(6): 1354-1361. DOI:10.3788/OPE.20192706.1354 |
| [2] |
余新明, 许志, 杨宜婧, 等. 一种基于薄膜压电传感器的床垫式无负荷睡眠监测系统. 航天医学与医学工程, 2019, 32(2): 144-149. DOI:10.16289/j.cnki.1002-0837.2019.02.009 |
| [3] |
Shin JH, Chee YJ, Jeong DU, et al. Nonconstrained sleep monitoring system and algorithms using Air-Mattress with balancing tube method. IEEE Transactions on Information Technology in Biomedicine, 2010, 14(1): 147-156. DOI:10.1109/TITB.2009.2034011 |
| [4] |
Chee Y, Han J, Youn J, et al. Air mattress sensor system with balancing tube for unconstrained measurement of respiration and heart beat movements. Physiological Measurement, 2005, 26(4): 413-422. DOI:10.1088/0967-3334/26/4/007 |
| [5] |
张先文, 张丽岩, 丁力超, 等. 基于心冲击信号的心率检测. 清华大学学报(自然科学版), 2017, 57(7): 763-767. DOI:10.16511/j.cnki.qhdxxb.2017.25.034 |
| [6] |
沈劲鹏, 王新安. 适用于床垫式生理信号监测系统的信号处理方法. 北京大学学报(自然科学版), 2018, 54(5): 921-926. DOI:10.13209/j.0479-8023.2018.012 |
| [7] |
王春武, 王旭, 龙哲, 等. 基于心冲击信号的心率提取算法. 东北大学学报(自然科学版), 2012, 33(8): 1103-1106. DOI:10.12068/j.issn.1005-3026.2012.08.009 |
| [8] |
Gregoire JM, Dale D, Van Dover R. A wavelet transform algorithm for peak detection and application to powder x-ray diffraction data. Review of Scientific Instruments, 2011, 82(1): 015105. DOI:10.1063/1.3505103 |
| [9] |
祝文颖, 冯志鹏. 基于改进经验小波变换的行星齿轮箱故障诊断. 仪器仪表学报, 2016, 37(10): 2193-2201. DOI:10.19650/j.cnki.cjsi.2016.10.004 |
| [10] |
张安跃, 唐志平, 郑航. PVDF压力传感器的冲击压电特性研究. 实验力学, 2009, 24(3): 244-250. |
| [11] |
Francis A, Muruganantham C. An adaptive denoising method using empirical wavelet transform. International Journal of Computer Applications, 2015, 117(21): 18-20. DOI:10.5120/20678-3515 |
| [12] |
蒋芳芳, 王旭, 杨丹, 等. 基于心冲击信号的呼吸率检测方法研究. 系统仿真学报, 2011, 23(11): 2357-2360. DOI:10.16182/j.cnki.joss.2011.11.028 |
 2021, Vol. 30
2021, Vol. 30



