航空公司运营计划包括航班计划、飞机排班计划和机组排班计划等, 其中机组排班计划是运营计划的重要组成部分. 近年来随着民航业的发展, 航线网络日益复杂, 民航管理局等相关部门为保障飞行安全制定了相关的行业规范, 例如CCAR-121-R6[1]等. 由于航线和约束的复杂性, 单纯使用手工模式进行排班是十分困难的, 另一方面, 航班计划在执行过程中难免会遇到由机械故障、天气原因或者机场调度等原因造成的航班变更, 因此在已有计划的基础上灵活地调整航班安排也是一个非常现实的需求. 由于人力成本的上升, 机组人员的收入水平提高, 机组排班的结果直接决定航空公司的实际机组成本支出, 从而影响航空公司的运营收益. 因此, 在满足相关约束下保障飞行安全的同时设计一个良好高效的算法来完成机组排班计划的编排对于航空公司提高运营效率和增加收益有着重要的现实意义.
本文提出一种基于可满足性模理论(Satisfiability Modulo Theories, SMT)的机组排班问题的优化求解方式. SMT在布尔可满足性理论(SAT)的基础上加入背景理论(例如, 算术运算、向量和数组等), 可以适用于更广泛的应用场景. 机组排班问题中既存在一些逻辑约束, 又存在一些数量约束, 因此考虑采用SMT来进行求解. 另一方面, 现代的SMT求解器都支持增量式的求解(incremental solving), 即可在求解的任何阶段, 增加或者删除约束, 而无需重新搜索整个状态空间, 这也为航班排班中灵活调整的实现带来的便利.
本文通过对机组排班问题的分析, 建立了机组排班问题的多目标优化模型, 将各种约束表述为一阶逻辑公式, 并利用SMT求解器Z3进行增量求解, 实现了一定规模的机组排班问题的优化求解.
本论文的组织结构如下: 在第2节, 对机组排班问题的定义、已有的研究工作以及SMT求解技术进行详细介绍. 在第3节, 提出机组排班的数学模型和相应算法. 在第4节, 通过实验对航班实例进行求解并对结果进行分析. 在第5节也是最后一节, 对全文的工作做出系统性的总结.
2 研究背景 2.1 机组排班问题概述机组排班计划问题是指在民航管理局相关适航文件和具体航空公司制定的一系列规定的前提下, 将航班计划内的各个航班合理的分配给机组飞行员和乘务人员执行的过程. 在航空公司运营总成本中, 机组成本是仅次于燃料成本的第二大费用[2], 由于机组成本比燃料成本具有更好的可控性, 通过合理的分配可降低一些不必要的额外成本, 为航空公司带来更多的收益. 为了保障飞行安全, 机组排班过程往往涉及大量的约束, 要满足一系列相关法律法规对飞行时间、人员要求等严格规定, 这使得机组排班模型复杂, 优化求解困难, 属于NP难问题[3].
机组排班计划问题一般分为两个子问题: 机组排班问题和机组人员指派问题. 其中机组排班问题又称为机组配对问题, 其任务是在满足相关约束条件下生成一系列可由机组执行的从机组基地出发并最终返回基地的航班任务环, 要求覆盖所有待执行的航班, 优化目标是任务环成本的最小化[4]. 机组人员指派问题[5]的任务是要将机组排班阶段生成的任务环中的任务合理的分配给具体的机组人员执行, 要求考虑任务分配的公平性原则. 本文主要研究机组排班问题.
2.2 已有的研究工作机组排班问题是复杂的组合优化问题, 通常可将其描述为集合分割问题(Set Partition Problem, SPP)或集合覆盖问题(Set Covering Problem, SCP). 本文将已有的研究工作分为确定性算法和非确定性算法.
非确定性算法方面, Kornilakis等[6]采用启发式两阶段求解方法, 先利用深度优先算法寻找所有可行任务环, 然后从所有任务环中选择最小成本的任务环组合, 选择了遗传算法来进行航班的组合优化. 赵天洋[7]对机组排班理论和算法进行分析, 比较了常用的遗传算法、蚁群算法和模拟退火算法的优缺点, 对机组排班各阶段进行分析设计, 将机组排班过程分为勤务生成、机组排班优化和机组人员指派3个部分, 采用改进的遗传算法进行优化求解. 吴苏阳[8]考虑机组排班中任务环组环的质量和效率, 从航空公司运营成本、生产计划的稳定性、生产计划质量和飞行时间均衡方面对飞行任务的组环进行优化, 采用遗传算法求解. Aggarwal等[9]提出了一种用于大规模复杂航班网络生成初始航班任务环的启发式算法, 采用分割和覆盖方法, 从大规模航班数据中随机分割部分航班生成任务环, 然后将优化求解后的任务环加入初始航班任务环(IFS)中, 直到所有航班被覆盖. 张文成等[10]提出改进二进制粒子群算法用于机组配对优化, 以机组利用率最大为优化目标, 利用深度优先搜索算法从航班计划表中生成初始航班配对, 在改进二进制粒子群算法寻优过程中引入惩罚因子和自适应权重, 提高了算法的速度和解的质量. Chen等[11]整合飞机排班和机组排班问题, 提出多目标组合优化模型, 采用NSGA-II(带精英策略的非支配排序的遗传算法)结合修复策略求解, 通过实际数据实验得出的时刻表比专家制定计划更优.
在确定性算法方面, Marsten等[12]建立了机组排班问题的集合分割模型, 采用拉格朗日松弛和次梯度优化方法进行求解. Graves等[13]采用列生成算法对机组排班问题进行求解, 系统分为生成器和优化器, 生成器负责生成候选航班配对传递给优化器, 优化器负责寻找使总成本最小的一组航班配对, 通过不断迭代至最优并覆盖所有航班. 蓝伯雄等[14]在机组排班阶段采用混合集合规划进行高层建模, 利用一阶逻辑和集合推理对机组排班问题进行表述, 将运筹学优化方法与业务逻辑相结合, 建立了贴近实际的机组排班模型. Zeighami等[15]集成了机组排班问题和机组人员分配问题, 综合考虑机组成本和飞行员喜好, 提出结合拉格朗日分解、列生成法和动态约束聚合的综合算法, 实验表明该方法能有效节省大量成本和满足机组人员喜好.
2.3 SMT求解技术介绍可满足性模理论(Satisfiability Modulo Theories, SMT)[16]是指检查给定的在相关背景理论(如算术、位向量、数组和未解释函数等)下一阶逻辑公式是否可满足的问题. 给定一个SMT公式F, 如果存在一组赋值使得F为真, 则称F是可满足的, 否则称F是不可满足的. SMT是一种说明性语言, 可以使用一阶逻辑语言描述问题的约束, 同时支持各种复杂约束, 能很好的描述NP及co-NP问题, 在优化问题求解[17]、程序验证[18]、静态分析[19]等领域有突出优势.
SMT的判定方法一般被称为SMT求解器(SMT solver), 目前主流的SMT求解器有Z3[20]、CVC4、Yices2等, 这些求解器都能较好的处理大规模工业化问题, 本文采用的是微软的Z3作为SMT求解器来求解机组排班问题.
Z3是微软组织开发的SMT求解器, 在扩展性、表达能力以及求解效率等方面都较为出色, 是目前最好用的SMT求解器之一. Z3在Github发布了开源的项目, 在近年来的SMT求解器的竞赛中一直处于领先的地位. Z3内部采用一种类似于Lisp的SMT-LIBv2语言[21], 同时也提供了包括C, C++和Python等常用的编程语言接口. 本文采用的Z3Py就是Z3提供的Python开发包, 可以方便约束求解和系统其它部分的接口. Z3支持多种理论, 不仅可以用于验证多个逻辑公式的可满足性, 也能给出一组满足约束的解; 此外还支持增量求解, 可以在不改变原问题基础上增加新的约束, 而无需重新计算, 加快了求解速度. Z3采用栈的方式, 可以在新约束不满足时回退到上一个阶段.
机组排班问题本质上是在一系列约束条件下的优化求解问题, 要满足民航局和航空公司制定的关于飞行安全的复杂适航条例, 属于NP难问题. SMT可以通过一阶逻辑公式很好的表达机组排班过程中各种复杂的约束, 在优化求解方面具有突出优势, SMT求解器Z3在扩展性、表达能力以及求解效率等方面都较为出色, 通过设置求解目标, 可以在满足相关约束的情况下高效地求解出问题的最优解.
3 机组排班模型及算法设计 3.1 问题的模型机组排班问题中机组排班问题通常用集合分割模型表示, 本文以最小化任务环总成本为主优化目标, 以最大化机组利用率为次目标建立多目标优化模型. 其中机组成本包括任务津贴、飞行津贴、在外过夜成本以及加机组成本等, 任务津贴是机组执行任务所要支付的必要成本; 飞行津贴是机组参与飞行时的补贴, 一般与飞行时间有关; 过夜成本是指机组在执行的某一天的任务中, 最后的航班降落机场为非基地机场, 无法回到基地休息而在外过夜产生的旅店成本; 加机组成本是一个机组为了完成某个任务而作为乘客搭乘另一个机组的航班到达目的地执行任务而产生的额外开支. 机组利用率是机组执行任务中有效的工作时间占据的比重, 等于机组飞行时间/机组执勤时间.
假设P是所有航班任务环的集合, p是P中一个任务环,
| $ Obj1:\min \sum\limits_{p \in P} {{c_p}{x_p}} $ | (1) |
任务环成本
| $\begin{gathered} {c_p} = {c_{\rm duty}}\sum\limits_{i \in p} {{c_f} \times f{t_i}} + \sum\limits_{d \in {D_{\rm overnight}}} {{c_{\rm overnight}} + {c_{\rm sit}}} \end{gathered} $ |
其中,
第二目标是最大化机组利用率, 假设I是所有待执行的航班集合, i是其中某个航班,
| $Obj2:\max \left( {{}^{\displaystyle\sum\limits_{i\in {{F}_{p,t}}}{f{{t}_{i}}}}\Bigg/{}_{\displaystyle\sum\limits_{i\in {{F}_{p,t}}}{d{{t}_{i}}}}\;} \right)$ | (2) |
假设
| $\sum\limits_{p \in P} {{a_{ip}}{x_p} = 1} ,\forall i \in I$ | (3) |
| $de{p_j} = ar{r_i}$ | (4) |
| $tde{p_j} - tar{r_i} \ge minct$ | (5) |
| $\sum\limits_{i \in {F_{p,t}}} {f{t_i} \le fts} $ | (6) |
| $\sum\limits_{i \in {F_{p,t}}} {d{t_i} \le maxdts} $ | (7) |
| $\left\{\begin{split} & date(tar{r_i}) - date(tde{p_j}) \le maxdays \\ &\forall i,j \in {F_p},i \ne j,\forall p \in P \end{split} \right.$ | (8) |
| ${a_{ip}},{x_p} \in \left\{ {0,1} \right\},{F_P},{F_{p,t}} \subseteq I$ | (9) |
其中, 式(3)是航班覆盖约束, 即每个航班有且仅有一次出现在选中航班任务环中.
式(4)是航班地点衔接约束, 要求后一个航班的起飞机场要与前一个航班的降落机场一致.
式(5)是航班过站时间约束, 要求后一个航班的出发时间与前一个航班的降落时间之差要大于最小航班连接时间限制.
式(6)为飞行时间约束, 要求在每一天机组总飞行时间不能超过最大飞行时间限制.
式(7)为执勤时间约束, 要求在每一天机组总执勤时间不能超过最大执勤时间限制.
式(8)为航班任务环总跨度约束, 即每个任务环的日期跨度不能超过最长时间跨度约束, date表示当前航班的日期.
式(9)中,
初始航班任务环生成阶段分成两步, 首先利用航班信息和相关约束通过改进的深度优先算法建立航班网络, 然后再利用DFS遍历所有航班网络生成初始航班任务环[22]. 航班网络的建立过程如算法1所示.
算法1. 航班网络的建立
输入: 航班集合I, 基地集合B, 所有相关约束C, 从机场出发的航班集合DepMap
输出: 航班网络集合
1. 初始化SB, EB //航班网络虚拟节点 , 分别表示从基地B出发和结束
2. for SB的每个子集Sb do //b为具体的基地机场
3. for i in DepMap[b] do //DepMap[b]表示从基地b出发的航班集合
4. add childNode i to Sb
5. for j in DepMap[iarr] do
6. if
7. add childNode j to i
8. if jarr=b;
9. add childNode Eb to j
10. return
11. else
12.
如算法1所示, 设虚拟起点为

|
图 1 航班网络连接示意图 |
航班网络建立完成后, 初始航班环生成如算法2所示. 对于
算法2. 初始航班任务环生成
输入: 航班网络
输出: 航班任务环P
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
下面通过举例来说明航班任务环的生成, 给定一组航班计划表, 如表1所示, 其中包括18个航班, 每个航班包括航班号、执飞机型、起飞/降落机场, 起飞/到达时间等信息, 该航班计划中有6个机场, 其中广州为基地机场, 其余为非基地机场.
首先生成航班连接网络, 再根据航班网络进行深度优先搜索寻找满足约束的航班任务环. 假设该航班计划表的基本约束条件如下: 机组每天的总飞行时间不超过8小时, 机组每天总执勤时间不超过14小时, 航班衔接时间不少于30分钟, 任务环每天的航班数不超过4个. 则生成初始可行航班任务环的步骤如下;
(1)按起飞机场对航班进行归类
该航班计划共有6个机场, 分别为广州、南昌、杭州、贵阳、桂林、长沙, 按起飞机场来划分可分为如下组合:
广州(0, 5, 7, 9, 11, 16); 南昌(1, 6, 8, 10); 贵阳(2, 3, 17); 杭州(4, 14); 桂林(12); 长沙(13, 15)
(2)生成航班连接网络
由于任务环都是从基地出发, 且该航班计划只有广州一个基地机场, 因此建立虚拟起始节点到所有从广州出发航班节点的连接, 如图2所示.
| 表 1 某航班计划表 |

|
图 2 初始航班网络 |
然后在初始网络的基础上, 遍历每一个节点对每个节点, 寻找与其降落机场对应的航班集合, 如0号航班的降落机场为南昌, 则对起飞机场为南昌的集合进行遍历, 验证其是否满足航班衔接约束, 若不满足则舍弃, 若满足则建立连接, 将其加入航班网络中, 以此类推, 直到当前节点的到达机场为基地机场广州为止, 然后将终止节点与虚拟终止节点
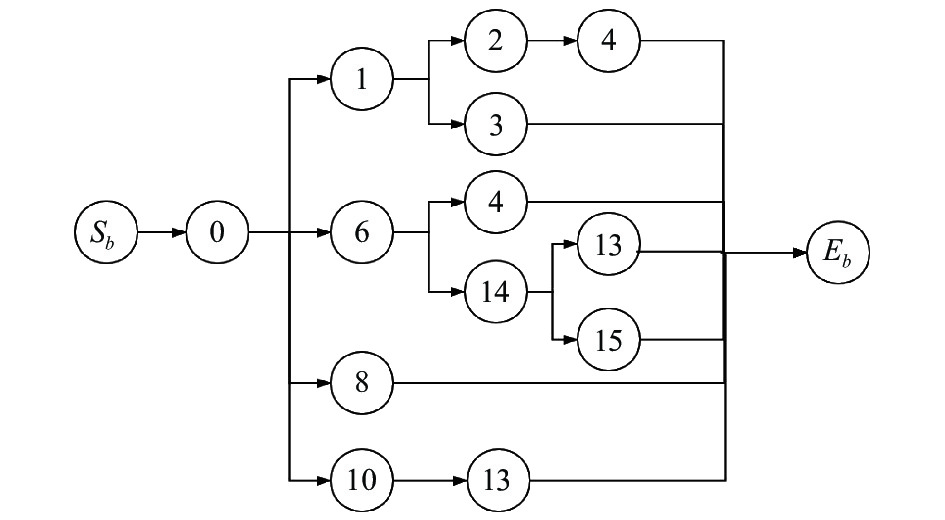
|
图 3 部分航班网络示意图 |
(3)搜索可行航班任务环
根据上述生成的航班网络, 利用深度优先搜索, 加入约束条件, 如飞行时间、执勤时间等, 得到满足约束条件的航班任务环, 最终生成了14个合法的可行航班任务环, 生成的航班环如表2所示.
| 表 2 生成的合法航班环 |
由表2可知, 生成的任务环的飞行时间和执勤时间均满足相应约束, 而并非所有航班环的机组利用率都是高效的, 机组利用率低导致机组在任务过程中空闲时间太长, 不能很好地体现机组的飞行价值, 而机组利用率也是优化求解的目标之一.
3.2.3 航空公司任务环生成实例为了验证任务环生成算法的有效性, 本节采用国内某航空公司一周航班计划的真实数据(对航班号进行了隐藏, 部分起飞和降落机场有所调整), 该航班计划共有7天, 共有576个航班, 每天的航班数量为80个左右, 主要基地机场为广州, 次基地有贵阳、三亚等, 根据航班网络生成算法建立航班连接网络, 由于页面限制, 图4仅展示第一天从广州基地出发的一个航班连接网络(省略了首尾的虚拟节点).
图4中每个节点代表一个航班, 节点内为航班的虚拟编号, 为方便展示, 在节点左右两边分别标注了该航班的起飞机场和降落机场.
航班网络生成后, 利用航班环生成算法生成了高质量的航班任务环2303个, 部分航班环实例如表3所示, 其中日期表示任务环中跨越的日期, 时间单位h和min表示小时和分钟.
3.3 优化求解算法初始航班任务环生成后, 利用SMT求解器Z3对模型进行表述, 假设输入航班集合为I, 初始航班任务环集合为IP, 定义Z3求解器模式为Optimize, 定义不解释函数PC(p)表示任务环p是否被选中, 函数的结果为Bool变量(true和false), 则基于Z3的增量求解的过程如算法3所示.
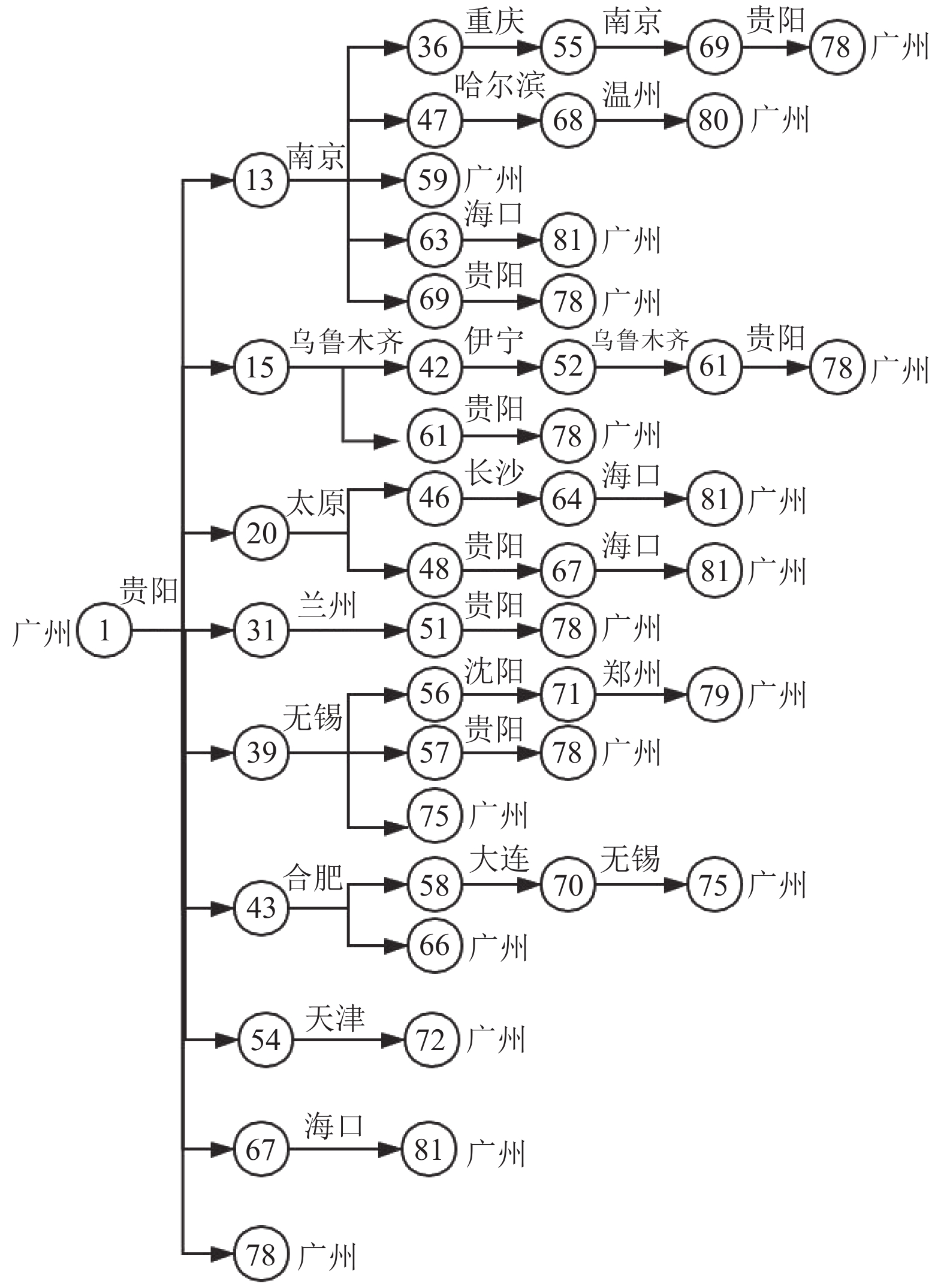
|
图 4 航班连接网络图 |
| 表 3 航班任务环实例 |
算法3. 基于Z3的增量优化求解
输入: 机场的集合AP, 基地集合BS, 航班的集合I(1.. n), 任务环生成函数GenPairing(), 参数level
输出: 最终任务环FP, 成本costs
1.
2. for
3.
4.
5. for
6.
7.
8.
9. for
10.
11. for each
12.
13.
14.
15.
16.
17.
18.
19. if
20.
21.
22.
23. else if TimeOut
24. return –1
25. else
26. return
如算法3所示, 输入的信息包括航班信息I, 航班任务环生成函数GenPairing(), 其中GenPairing()可以输入的参数level生成不同层次的任务环, 如level=0时生成当天返回基地的任务环, level=1时生成当天未返回基地的任务环等.
算法遍历level依次生成不同层次的任务环, 5–7行是航班覆盖约束, 要求每个航班至少被1个任务环覆盖,
下面仍以表1的航班计划表为例, 阐述优化求解的过程. 航班总数为18, 经过GenPairing(0)生成了第一阶段当天返回基地的初始航班任务环数量为16, 然后对其增加相应的约束进行Check()检查, 发现结果为unsat, 使部分约束失效后进行下一阶段GenPairing(1)生成当天未返回基地的不完全任务环11-17、0-10等, 由于未返回基地增加过夜成本, 加入先前的任务环中, 添加相应约束进行求解, 仍为unsat, 再下一阶段GenPairing(2)增加覆盖次数较少的航班2、7、10等加入任务环后, 结果为sat, 最终生成的任务环如表4所示.
| 表 4 优化求解后的任务环 |
由最后的结果可知, 生成的任务环覆盖了所有的航班, 且每个航班有且仅被覆盖一次, 同时, 总成本也较低, 机组利用率超过了0. 6, 说明该方法是有效的.
4 实验分析 4.1 实验环境及实验分析本文对航空公司机组排班问题进行优化求解, 实验环境选择个人电脑, CPU为AMD Ryzen5 1600X 6核心12线程, 内存16 GB, Win10系统, 编程语言选择Python, SMT求解器选择Python版本的Z3Py[23], 实验数据来自Kasirzadeh等[24]提供的航空公司的一组航班计划数据. 本文选取前7天航班计划数据来验证求解结果和性能, 按照跨越天数将其分为7组, 数据的基本信息如表5所示, 部分航班时刻表如表6所示.
表6中, 表头leg_nb表示航班编号, airport_dep与airport_arr分别表示航班的出发机场和到达机场, date_dep、hour_dep表示航班出发的日期和时间, date_arr、hour_arr表示航班到达日期和到达时间.表中, BASE*表示该机场为基地机场, AIR*表示机场为非基地机场. 经过改进的航班网络生成和DFS算法, 有效的减少了生成的初始航班任务环的数量,按照不同的level参数, 生成用于求解的航班环数量如表7所示.
优化求解阶段, 利用Z3的增量求解机制, 依次对不同level生成的任务环进行check检查其是否满足相应约束, 直到结果为sat, 进行优化求解. 实验表明, 当level=2时各组数据生成的任务环均可满足相应的约束.
假设机组每天最大飞行时间为8小时, 最大执勤时间为14小时, 最小衔接时间为30分钟, 任务津贴为1000, 每小时飞行津贴为400, 过夜成本为500, 加机组成本为500, 机组在任务开始前45分钟报到, 任务结束后30分钟完成执勤, 优化求解后生成最终的航班任务环及机组利用率等结果如表8所示.
| 表 5 航班数据基本信息 |
| 表 6 部分航班时刻表 |
| 表 7 各组航班环数量 |
| 表 8 模型求解结果 |
从求解结果可知, 该算法能有效的从给定的航班计划中选择符合各项约束的任务环. 经过验证, 生成的任务环能覆盖所有航班, 且机组利用率均超过了55%, 有效的减少了机组的空闲等待时间, 有效的缩短了机组执勤时间, 同时最小化的成本可为航空公司减少一定的机组成本支出, 增加航空公司的收益.
4.2 实验对比为了验证实验算法的性能, 本文与Agustín等[25]提出的基于偏向随机化的多起点元启发式算法以及人工编排方案进行比较分析, 实验数据来自某小型航空公司的真实案例, 数据来源于文献[25]. 共有41个航班, 跨越5天, 航班的最小连接时间为45 min, 只有一个基地机场Madrid (MAD).
经过实验, 得出实验结果如表9所示.
| 表 9 实验结果对比 |
从实验结果可知, SMT、M-BR与人工编排相比生成的任务环数量更少, 飞行时间更短, 机组成本更低, 这是由于人工编排产生了许多不必要的加机组航班, 增加了飞行时间和机组成本; SMT相比于M-BR, 机组的利用率更高且求解时间更短.
通过分析实验结果, 本文提出的SMT算法相较于人工和M-BR算法, 求解效率更高, 总值勤时间更少, 机组利用率更高, 更符合航空公司机组排班阶段对任务环质量的要求, 可以有效的减少机组成本和提高机组利用率.
5 总结本文采用基于SMT的研究方法, 对航空公司运营计划中机组排班计划问题的机组排班问题进行了研究, 综合考虑了民航管理局等制定的关于飞行安全、人员要求等多种约束, 建立了基于SMT的机组排班优化模型, 采用改进的深度优先搜索算法生成初始航班任务环, 并利用SMT求解器Z3进行模型的优化求解, 并使用增量求解. 实验表明, 改进的DFS算法能更快速的生成更少更优质的初始航班任务环, 基于SMT的Z3求解器可以更好的表述约束和求解约束, 并可以增量求解, 最终生成机组利用率高且质量较好的航班任务环, 帮助航空公司制定更好的排班计划以及节约机组成本, 增加收益.
在之后的研究中, 可对机组排班的下一个阶段机组人员分配问题进行研究, 制定完整的机组排班计划, 以及在考虑延误等突发情况下如何增加机组排班的鲁棒性进行进一步的研究, 更贴近实际, 减少航班延误造成的损失.
| [1] |
CCAR-121 R6大型飞机公共航空运输承运人运行合格审定规则. https://www.woair.com/zhengfu/news/2020-06-09/19.html. (2020-06-09).
|
| [2] |
Aggarwal D, Saxena DK, Emmerich M, et al. On large-scale airline crew pairing generation. 2018 IEEE Symposium Series on Computational Intelligence (SSCI). Bangalore: IEEE, 2018. 593–600.
|
| [3] |
McCarver M. Airline Crew Scheduling Problem. 2019 NCUR, 2019.
|
| [4] |
Haouari M, Mansour FZ, Sherali HD. A new compact formulation for the daily crew pairing problem. Transportation Science, 2019, 53(3): 811-828. DOI:10.1287/trsc.2018.0860 |
| [5] |
Zhang ZZ, Zhou MC, Wang JH. Construction-based optimization approaches to airline crew rostering problem. IEEE Transactions on Automation Science and Engineering, 2020, 17(3): 1399-1409. DOI:10.1109/TASE.2019.2955988 |
| [6] |
Kornilakis H, Stamatopoulos P. Crew pairing optimization with genetic algorithms. In: Vlahavas IP, Spyropoulos CD, eds. Methods and Applications of Artificial Intelligence. Berlin: Springer, 2002. 109–120.
|
| [7] |
赵天洋. 航班机组自动排班系统研究[硕士学位论文]. 沈阳: 沈阳理工大学, 2016.
|
| [8] |
吴苏阳. 航空公司飞行任务的自动组环优化算法研究与实现[硕士学位论文]. 上海: 复旦大学, 2016.
|
| [9] |
Aggarwal D, Saxena DK, Bäck T, et al. On initializing airline crew pairing optimization for large-scale complex flight networks. arXiv: 2003.06423, 2020.
|
| [10] |
张文成, 熊静, 张虹, 等. 基于改进二进制粒子群算法的机组配对优化. 上海工程技术大学学报, 2020, 34(1): 34-40. DOI:10.3969/j.issn.1009-444X.2020.01.006 |
| [11] |
Chen CH, Chou FI, Chou JH. Multiobjective evolutionary scheduling and rescheduling of integrated aircraft routing and crew pairing problems. IEEE Access, 2020, 8: 35018-35030. DOI:10.1109/ACCESS.2020.2974245 |
| [12] |
Marsten RE, Shepardson F. Exact solution of crew scheduling problems using the set partitioning model: Recent successful applications. Networks, 1981, 11(2): 165-177. DOI:10.1002/net.3230110208 |
| [13] |
Graves GW, McBride RD, Gershkoff I, et al. Flight crew scheduling. Management Science, 1993, 39(6): 736-745. DOI:10.1287/mnsc.39.6.736 |
| [14] |
蓝伯雄, 张米. 机组排班的混合集合规划方法研究. 运筹与管理, 2014, 23(2): 175-182. DOI:10.3969/j.issn.1007-3221.2014.02.024 |
| [15] |
Zeighami V, Saddoune M, Soumis F. Alternating Lagrangian decomposition for integrated airline crew scheduling problem. European Journal of Operational Research, 2020, 287(1): 211-224. DOI:10.1016/j.ejor.2020.05.005 |
| [16] |
金继伟, 马菲菲, 张健. SMT求解技术简述. 计算机科学与探索, 2015, 9(7): 769-780. DOI:10.3778/j.issn.1673-9418.1405041 |
| [17] |
Sebastiani R, Tomasi S. Optimization in SMT with LA(Q) cost functions. Proceedings of the 6th International Joint Conference on Automated Reasoning. Manchester: Springer, 2012. 484–498.
|
| [18] |
Klein G. Operating system verification-an overview. Sadhana, 2009, 34(1): 27-69. DOI:10.1007/s12046-009-0002-4 |
| [19] |
Blackham B, Liffiton M, Heiser G. Trickle: Automated infeasible path detection using all minimal unsatisfiable subsets. 2014 IEEE 19th Real-Time and Embedded Technology and Applications Symposium (RTAS). Berlin: IEEE, 2014. 169–178.
|
| [20] |
De Moura L, Bjørner N. Z3: An efficient SMT solver. Proceedings of the Theory and Practice of Software, 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2008. 337–340.
|
| [21] |
The SMT-LIBv2 language and tools: A tutorial. http://smtlib.github.io/jSMTLIB/SMTLIBTutorial.pdf. (2013-11-23).
|
| [22] |
鲁红珍. 航空公司机组航班任务串优化方法研究[硕士学位论文]. 广汉: 中国民用航空飞行学院, 2012.
|
| [23] |
The Z3 theorem prover. https://github.com/Z3Prover/z3. [2020-12-10].
|
| [24] |
Kasirzadeh A, Saddoune M, Soumis F. Airline crew scheduling: Models, algorithms, and data sets. EURO Journal on Transportation and Logistics, 2017, 6(2): 111-137. DOI:10.1007/s13676-015-0080-x |
| [25] |
Agustín A, Gruler A, De Armas J, et al. Optimizing airline crew scheduling using biased randomization: A case study. Proceedings of the 17th Conference of the Spanish Association for Artificial Intelligence. Salamanca: Springer, 2016. 331–340.
|
 2021, Vol. 30
2021, Vol. 30


