三峡升船机是世界建设规模最大的全平衡齿轮齿条爬升式升船机, 为了维护设备正常运转, 工作人员需每日对船厢设备进行巡视点检. 三峡升船机设备巡视点检是一种预防性的、主动性的、周期性的设备检查过程, 是设备运行管理的重要组成部分[1]. 三峡升船机设备巡视的路径规划可以视为TSP旅行商问题, 在实现遍历每个目标点的基础上实现路线最短. 蚁群算法是近几年优化领域中新出现的一种启发式仿生类并行智能进化系统, 该算法采用分布式并行计算和正反馈机制, 蚁群算法的特征适用于巡视问题的求解[2,3].
1 点检路线空间结构模型 1.1 巡视点检特点根据三峡升船机设备巡视要求, 现场管理人员需在早、中、晚班期间完成升船机船厢设备的巡视检查. 点检人员使用手持式点检仪, 通过识别RFID设备识别卡, 读取点检目录, 人为确认设备状态并记录[1]. 整个点检路线完成后, 将点检仪采集到的数据上载到系统管理软件中[4]. 所有点检点位识别卡均被读取则视为一轮巡视的结束, 三峡升船机设备巡视存在遍历性要求. 三峡升船机船厢在结构上可分为4层, 内部共有4个驱动点及相关电气控制设备. 由于升船机结构的对称性, 不同区域的巡视线路呈现局部相似性. 根据船厢内部设备分布和步行线路布置, 部分巡视点位存在路线唯一性.
1.2 点检路线无向加权图通过测量巡视点位之间的相互距离可建立点位之间的邻接矩阵, 邻接矩阵表示点位之间的相互距离和通过关系. 结合巡视点检结合巡视路线的遍历性、局部相似性及路线唯一性特点, 建立巡视点位无向加权图, 巡视路线无向加权图如图1所示.

|
图 1 白班及中班巡视路线无向加权图 |
基于实际巡视情况, 将距离相隔较近的巡视点位进行合并, 例如船厢电气动力室与电气传动室点位距离较近, 同一区域合并为一个点位. 同时不考虑单向出入口点位, 例如上下厢头船厢门启闭机点位与对应驱动点点位之间有且仅有唯一往返路线.
图1(a)表示白班期间船厢设备巡视点位的加权无向图, 图1(b)表示中班期间船厢设备巡视点位的加权无向图. 圆圈表示各个巡视点位, 点位之间都允许双向通行. 圆圈之间的数字表示加权权重, 其加权权重由点位间的相互距离和空间位置关系共同决定.
1.3 建立巡视点位空间坐标传统的蚁群算法多适用于解决二维平面路径规划问题, 而升船机船厢在垂直方向具有多层结构, 不同层次直线距离较近的目标位无法直接连接, 因此难以将升船机巡视路线展开到二维平面进行研究. 根据图1中点位之间的加权权重, 在笛卡尔坐标系中设定巡视点位所在的空间坐标, 表1、表2表示了巡视点位的空间坐标. 该空间坐标基于无向图加权权重得来, 坐标点之间的直线距离基本符合权重关系, 但坐标与巡视点位实际位置并不相同.
| 表 1 白班巡视点位空间坐标 |
| 表 2 中班巡视点位空间坐标 |
2 建立蚁群算法模型 2.1 蚁群算法计算流程
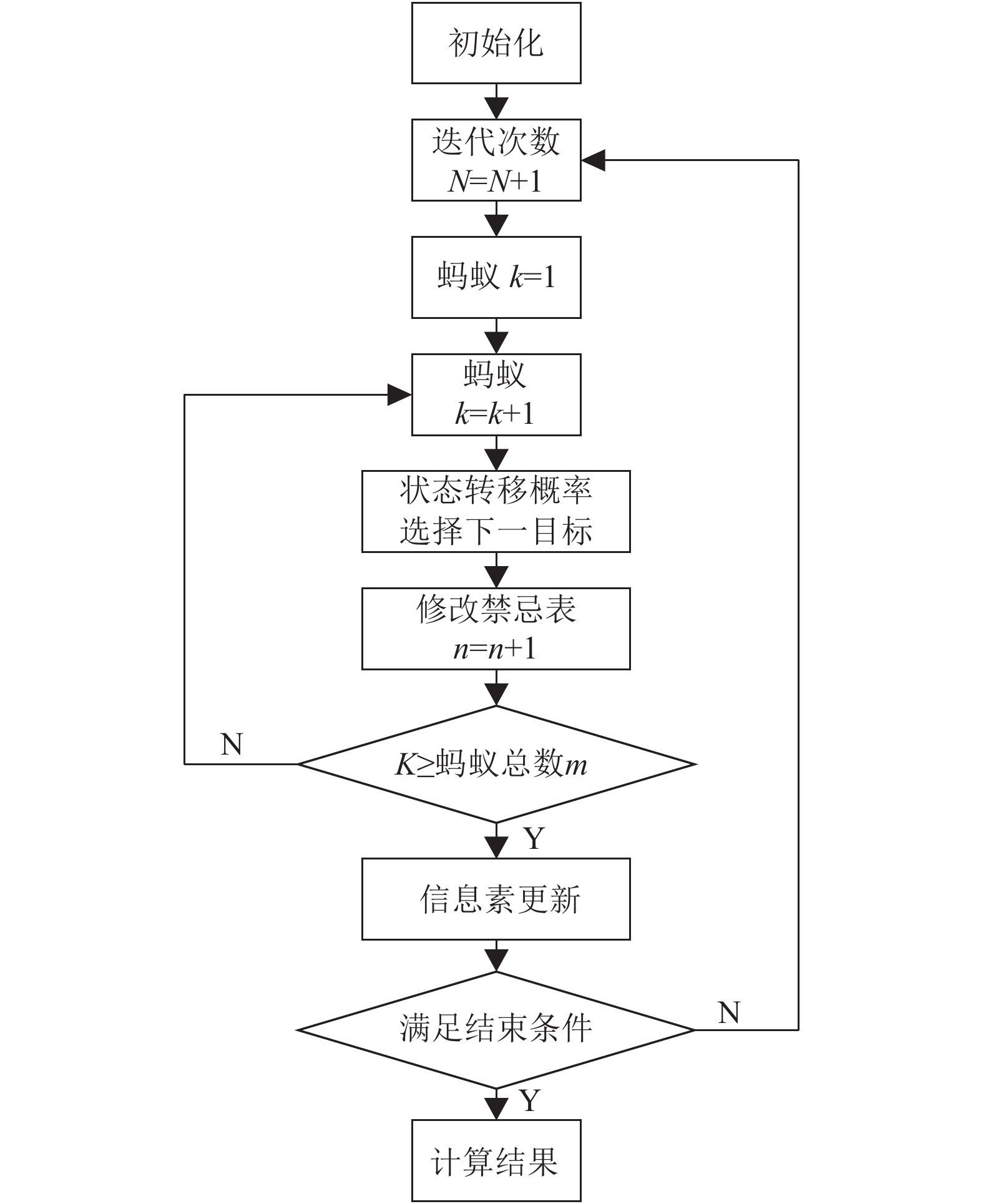
当蚂蚁在食物和巢穴之间往返时, 他们会在经过的路线上铺设一种被称为信息素的化学物质, 蚂蚁可以嗅到这种信息素, 并且选择信息素浓度最大的线路, 经过一条线路的蚂蚁越多, 这条线路上的信息速度浓度也越大, 更多的蚂蚁就会选择这条线路, 蚂蚁的这种正反馈行为够帮助它们很快找到最短觅食线路, 蚁群算法就是受到这种行为启发, 以人工蚂蚁模拟真实蚂蚁行为的分布式算法[5]. 蚁群算法的基本流程如图2.
|
图 2 蚁群算法流程图 |
该算法假设将m只蚂蚁放入n个随机选择的巡视点位中, 每只蚂蚁根据状态转移概率选择下一个点位, 状态转移概率与信息素浓度或者点位间的距离有一定关系. 每只蚂蚁完成路线后, 信息素将会更新. 当所有数量的蚂蚁完成巡视路径, 或者迭代次数达到上限值后, 流程将中断并输出最优解, 一般即为最佳路径. 本次算法采用ant-cycle模型进行计算, 该模型更偏重于考虑整体信息, 避免计算中产生局部最优, 该模型更加适合TSP问题[6].
2.2 基本参数设置蚁群算法中, 初始化参数包括以下几类: (1)蚂蚁数量m, 一般设置为目标数的1.5倍, 蚂蚁数量过大会导致信息素浓度相差较小, 收敛速度减慢. 白班巡视点位为18个, 设定蚂蚁数量为m=27. 中班巡视点位为16个, 设定蚂蚁数量为m=24. (2)信息素因子α, 反映了信息素对路径选择的重要程度, 其取值范围通常在[1, 4]之间. α设置过大会降低路径选择的随机性; 过小容易过早陷入局部最优, 设置信息素因子为α=2. (3)启发函数因子β, 反映了启发式信息在路径选择中的重要程度, 其值影响收敛速度, 如果值设置过大, 虽然收敛速度加快, 但是易陷入局部最优; 其值过小很难找到最优解, 设置启发函数因子为β=4. (4)信息素挥发因子ρ, 反映了信息素挥发情况. 当ρ取值过大时, 容易影响随机性和全局最优性, ρ取值范围通常在[0.2, 0.5]之间, 设置信息素挥发因子0.2. (5)信息素常数Q, 表示每一轮蚂蚁释放的信息素总量. Q越大则收敛速度越快, 但是容易陷入局部最优, 设置信息素常数为Q=50[6].
状态转移概率表示蚂蚁选择下一个目标的可能性, 其概率数值与路径的信息素浓度, 还有路径的启发信息相关, 状态转移概率的表达式如下:
| $p_{i j}^{k}(t)= \begin{cases}{\left[\tau_{i j}(t)\right]^{\alpha} \cdot\left[\eta_{i j}\right]^{\beta} \Bigg / \displaystyle\sum\limits_{j \in { allowed }}\left[\tau_{i j}(t)\right]^{\alpha} \cdot\left[\eta_{i j}\right]^{\beta},} \\ \qquad\qquad\qquad\qquad\qquad j \in { allowed } \\ 0, \qquad\qquad\qquad\qquad\;\; \text { 其他 }\end{cases}$ | (1) |
式中,
若蚂蚁已经到达过点位j, 则计算转移概率为零, 实际在程序中表示为无穷小的数值, 蚂蚁下次只会选择未到达的目标点位.
随着计算程序的进行, 蚂蚁不断堆积信息素. 为了避免信息素一直在路径上残留, 在每只蚂蚁完成路径规划后, 需对路径残留的信息素总量进行更新. 以t时刻作为初始值, 经过n时刻后, 其中一条路径(i, j)上的信息素浓度可更新为:
| ${\tau _{ij}}{\rm{(}}t + n{\rm{)}} = {\rm{(1 - }}\rho {\rm{)}}{\tau _{ij}}{\rm{(}}t{\rm{)}} + \Delta {\tau _{ij}}{\rm{(}}t{\rm{)}}$ | (2) |
| $\Delta {\tau _{ij}}{\rm{(}}t{\rm{)}} = \sum\limits_{k = 1}^m {\Delta {\tau _{ij}}^k{\rm{(}}t{\rm{)}}} $ | (3) |
式中,
根据蚁群算法的原理, m只蚂蚁将通过信息素浓度的正反馈选择出一条最佳路径, 该路径相对于其他路径信息素总量更高, 通过这种方法可以在三峡升船机船厢中选择出一条最适合的巡视点检路线.
3 计算结果及参数对比基于Matlab软件, 可实现蚁群算法的迭代计算. 在程序计算过程中, 局部的巡视点位之间的距离权重相差不大, 例如中班的3.3#点位与3.2#、4.2#点位的距离, 计算中存在局部最优的情况, 中班巡视路线的最短距离和平均轨迹的收敛性不如白班巡视路线. 在基本蚁群算法当中, 理论上要求所有蚂蚁选择的同一路线为最优路线, 但实际巡视路线的计算中, 受到循环次数和实际路线点位的影响, 并不需要所有蚂蚁走出最佳路径, 只需要一只找到最短路径即可[7], 因此升船机巡视路线以距离最短且实际可通过的路径作为最优解.
3.1 白班巡视路线计算结果图3(a)展示了基于蚁群算法计算出的白班巡视最佳巡视路线, Matlab程序执行时间为1.65 s, 以零层甲板4#为巡视起点, 白班的最佳巡视路线巡视点位依次为4#, 4.1#, 4.2#, aa#, bb#, 1.2#, 1.1#, 1#, A#, 2#, 2.1#, 2.2#, cc#, dd#, 3.2#, 3.1#, 3#, B#, 4#, 根据此条巡视路线, 人员需在船厢负三层同步轴走道完成上下游之间的移动, 而南北侧的移动需通过船厢零层的防撞桁架走道.

|
图 3 白班巡视最佳路线及收敛轨迹 |
该计算路线虽符合升船机现场巡视实际情况, 但在升船机船舶进出厢, 或者船厢上下行时, 巡视人员无法通过防撞桁架走道, 此时只能通过船厢负二层走道1.2#–2.2#, 3.2#–4.2#实现南北侧之间的移动. 图3(b)说明了计算过程中巡视路线的最短距离收敛轨迹与平均距离收敛轨迹, 收敛轨迹显示计算过程正常收敛[8].
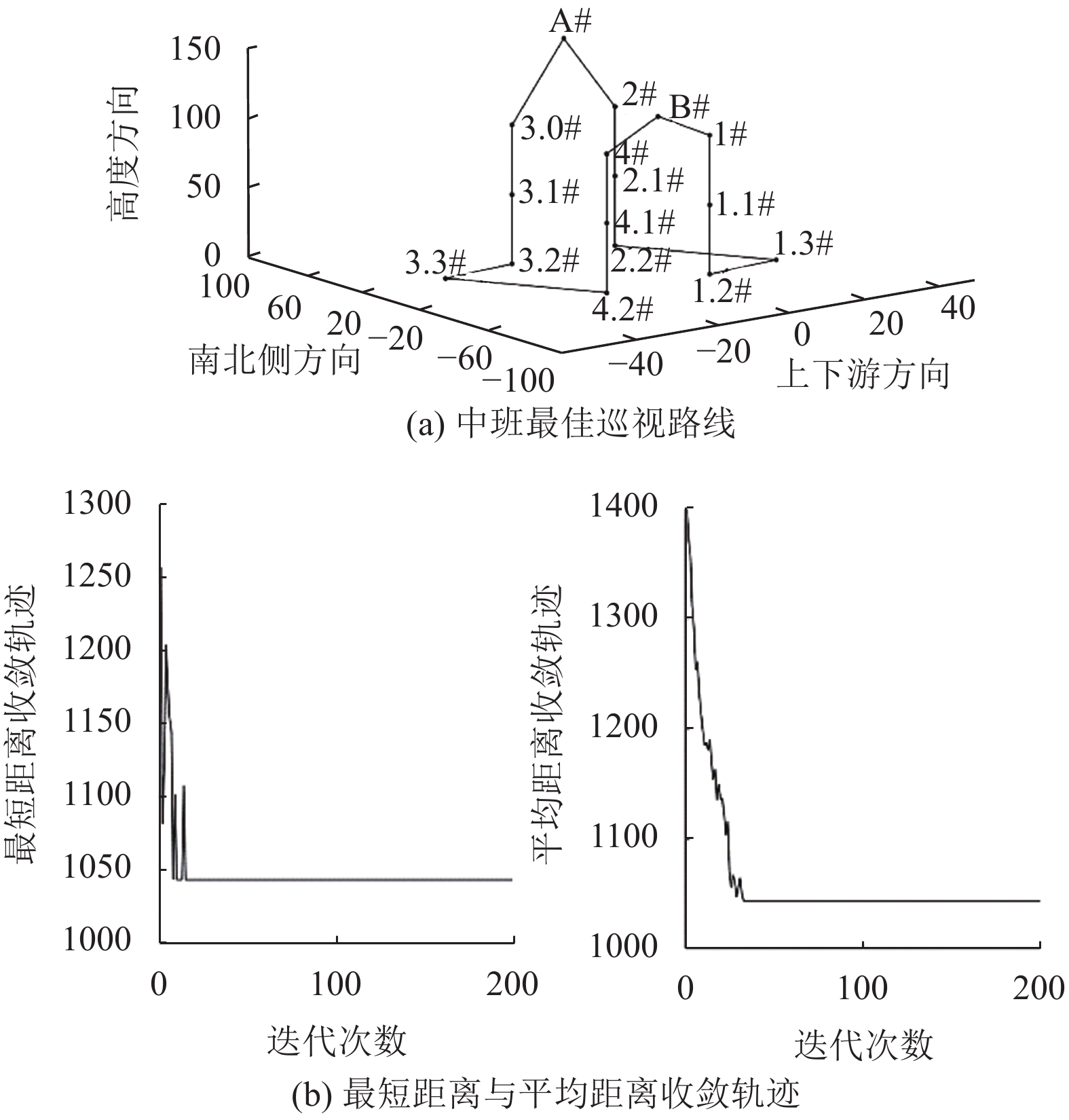
3.2 中班巡视路线计算结果图4(a)展示了基于蚁群算法计算出的中班巡视最佳巡视路线, Matlab程序执行时间为1.288秒, 同样以船厢零层甲板4#为巡视起点, 中班的最佳巡视路线巡视点位依次为4#, 4.1#, 4.2#, 3.3#, 3.2#, 3.1#, 3#, A#, 2#, 2.1#, 2.2#, 1.3#, 1.2#, 1.1#, 1#, B#, 4#. 根据此条巡视路线, 人员需在船厢零层甲板完成上下游之间的移动, 而南北侧的移动需通过船厢负二层走道, 该计算路线符合升船机现场巡视实际情况, 巡视路线不会因为船厢运行工况发生改变. 图4(b)说明了计算过程中巡视路线的最短距离收敛轨迹与平均距离收敛轨迹, 收敛轨迹显示计算过程正常收敛.
|
图 4 中班巡视最佳路线及收敛轨迹 |
4 结论
本文以三峡升船机运行班组白班及中班的巡视路线作为研究对象, 目标是找到一条到达所有设备巡视点位的前提下人员行走距离最短的路线. 基于蚁群算法, 能够模拟一定数量蚂蚁在巡视点位之间作出路线选择, 最终分别计算出白班和中班的一条可通行的巡视路径, 为三峡升船机现场管理人员的巡视提供了路线参考. 同时, 本文需在以下两点作出改进:
(1)本文建立了巡视点位无向加权图及相关空间坐标, 中空间坐标仅考虑了距离和现场点位布置因素, 与升船机船厢内实际设巡视点位坐标存在偏差, 同时在蚁群算法计算中可能产生进一步的计算误差.
(2)本文基于三峡升船机巡视路线进行研究, 经过建立优化空间模型, 巡检点位数量与实际点位相比有所减少, 在蚁群算法的模拟过程中存在计算效率较低的情况. 下一步需进行蚁群算法参数优化以及人员实际巡视效率提升等方面做更多研究.
| [1] |
李山, 邹斌斌. 三峡升船机设备巡视点检的分析与思考. 技术与市场, 2019, 26(9): 157. |
| [2] |
段海滨, 王道波, 于秀芬. 蚁群算法的研究现状及其展望. 中国工程科学, 2007, 9(2): 98-102. DOI:10.3969/j.issn.1009-1742.2007.02.017 |
| [3] |
张赤斌, 王兴松. 基于蚁群算法的完全遍历路径规划研究. 中国机械工程, 2008, 19(16): 1945-1949. DOI:10.3321/j.issn:1004-132X.2008.16.013 |
| [4] |
吴鹏, 欧阳升, 王婷婷, 等. 三峡升船机设备点检系统设计与实现. 自动化技术与应用, 2018, 37(4): 94-99. DOI:10.3969/j.issn.1003-7241.2018.04.021 |
| [5] |
叶志伟, 郑肇葆. 蚁群算法中参数α、β、ρ设置的研究——以TSP问题为例
. 武汉大学学报(信息科学版), 2004, 29(7): 597-601. |
| [6] |
刘刚, 郭旭红, 冯志华, 等. 蚁群算法在TSP中的仿真应用及最优参数选择研究. 苏州大学学报(工科版), 2007, 27(1): 56-59. |
| [7] |
杜衡吉, 李勇. 蚁群算法中参数设置对其性能影响的研究. 现代计算机, 2012(13): 3-7. DOI:10.3969/j.issn.1007-1423-B.2012.13.001 |
| [8] |
段海滨, 王道波. 蚁群算法的全局收敛性研究及改进. 系统工程与电子技术, 2004, 26(10): 1506-1509. DOI:10.3321/j.issn:1001-506X.2004.10.049 |
 2021, Vol. 30
2021, Vol. 30


