知识图谱(Knowledge Graph, KG)[1]作为实体关系的语义网络, 在相关实体搜索的应用中至关重要, 是搜索引擎的重要支撑技术[2]. 基于KG的相关实体搜索旨在根据给定的实体, 在KG中搜索与此实体相关的候选实体集合, 并按照候选实体与查询实体间的相关度对候选实体进行排序并返回结果, 以提高用户的搜索体验. 事实上, 随着互联网的高速发展, Web文档快速产生, 反映了现实世界不断演化的知识, 与KG中的知识共同描述了实体间的相关关系. 因此, 如何有效地表示实体在KG和Web文档中的关系信息, 进而准确地搜索与给定实体相关的候选实体, 并对候选实体进行排序, 对提升相关实体搜索的准确性具有重要意义. 虽然现有方法能够有效地获取相关实体, 减少用户搜索时需要过滤的无用信息, 但仍存在如下挑战:
(1) 与实体相连的不同关系能够表示实体不同的语义[3,4], 因此, 需要一种能够有效表示不同关系中实体的语义并准确搜索候选实体的方法.
(2) 由于Web文档与KG共同描述了实体间的相关关系, 为了准确地对候选实体进行打分排序, 需要一种能够根据实体在Web文档与KG中的关系信息来计算候选实体与查询实体间相关度的方法.
针对挑战(1), 现有方法主要根据查询实体的邻居节点来搜索候选实体, 如Huang等[5]使用与查询实体直接相连的实体作为候选实体集, Reinanda等[4]获取以查询实体为中心的k阶子图, 并基于子图的路径信息搜索候选实体. 上述方法在小规模KG中表现尚可, 而当KG规模较大时, 需要搜索的候选实体会出现在查询实体的邻居实体集外, 导致无法正确搜索到候选实体. 对此, 现有的表示学习方法[5-7]将高维、复杂的KG映射到低维的向量空间中, 进而降低在大规模KG上的计算开销. 为了更加有效地搜索候选实体, 本文基于TransH模型[7]提出候选实体搜索算法, 首先去除对查询实体不重要的关系, 降低搜索的时间代价. 然后通过KG的嵌入向量计算出实体在各关系对应超平面上的投影, 作为不同关系下实体的语义表示. 由于候选实体与查询实体有共同的语义特征[2], 因此, 为了有效地搜索候选实体, 我们根据实体的语义相似度对各超平面中的投影进行聚类, 进而得到与查询实体有共同语义特征的候选实体.
针对挑战(2), 现有方法大多基于KG来计算实体相关度, 例如, Milne等[8]提出了WLM方法, 基于KG中实体所对应Wikipedia页面的超链接完成实体间的相关度计算. Ponza等[9]提出了TSF (Two-Stage Framework)方法, 利用KG实体间的连接关系构建带权有向图, 并基于CoSimRank算法[10]来计算实体间的相关度. 这些算法能反映KG中实体间的相关性, 但由于现有KG的知识仍不完整[11], 导致计算结果不够准确. 对此, Yamada等[12]通过将描述实体的词汇和KG中的实体共同映射到向量空间, 以计算实体间的相关性. 该方法虽能将词汇与KG相结合来发现实体间的相关性, 但在映射过程中会损失KG实体间的关系信息, 导致计算结果不够准确. 因此, 为了更准确地计算查询实体与候选实体间的相关度, 我们提出实体无向带权图模型(Entity Undirected Weighted Graph, EUWG). 首先, 以查询实体与候选实体作为图中节点, 基于查询实体与候选实体间的相关关系来构造无向边. 然后, 通过量化实体在KG向量空间和Web文档中体现出的相关性, 计算EUWG边上的权重, 得到查询实体与候选实体相互间的相关度, 并基于该模型提出一个候选实体打分函数, 通过遍历EUWG中实体间的路径计算候选实体的分数, 完成候选实体的排序.
最后, 使用Wikidata数据集, 对所提出的方法进行了实验测试和性能分析, 与现有的候选实体搜索算法和实体相关度计算模型进行比较, 验证了本文提出方法的有效性.
2 候选实体搜索 2.1 查询实体关系选择定义1.
首先, 将给定的查询实体记为eq, 为了增加搜索候选实体的效率, 本文提出从全局重要度和局部重要度两方面来度量关系r对eq的语义表示能力, 去除对eq语义表示能力弱的关系, 减少需计算的关系数量.
(1) 全局重要度, 即关系r在KG中的重要程度. r在Gkg中出现的频率越高, 其对eq的特殊性就越小, 重要性也就越小. 按以下方式计算r对eq的全局重要度:
| ${I_1}({e_q},r) = \frac{1}{{r'}}$ | (1) |
其中, r'为r在Gkg中出现的次数.
(2) 局部重要度, 即关系r在以查询实体eq为中心的局部子图中的重要程度. 将KG中与eq直接相连的边构成的集合记为R'(eq), r在R'(eq)中出现的次数越多, 说明eq通过r连接的实体越多, 进而r对eq就越重要. r在R'(eq)中出现的次数与其重要程度成反比, 计算公式如下:
| ${I_2}({e_q},r) = \frac{{r''}}{{\left| {R'({e_q})} \right|}}$ | (2) |
其中, r"为关系r在R'(eq)中出现的次数, |R'(eq)|为R'(eq)中三元组的个数.
然后, 使用超参数α来平衡上述因素对关系r语义表示能力的贡献. 为了统一I1(eq, r)和I2(eq, r)的取值区间, 使用最大最小归一化函数(Min-Max Scaling)[13]对全局重要度和局部重要度进行处理, 计算公式如下:
| $I\left( {{e_q},r} \right) = \alpha Nor\left( {{I_1}\left( {{e_q},r} \right)} \right) + \left( {1 - \alpha } \right)Nor\left( {{I_2}\left( {{e_q},r} \right)} \right)$ | (3) |
其中, α∈[0,1], 为衡量各因素贡献比重的超参数, Nor(·)为最大最小归一化函数.
最后, 为了提高候选实体搜索的效率, 通过式(3)计算KG中各关系对查询实体eq的语义表示能力并对各关系进行排序, 选择其中得分最高的前k个关系, 记为集合S.
2.2 查询实体关系选择首先, 将KG中的实体通过训练嵌入到向量空间中, 得到对应的实体向量集E={e1, e2,…, en}, 其中, ej∈E (1≤ j ≤n)是实体ej的向量表示. 将与关系集合S对应的超平面法向量集记为D={d1, d2,…, dk}, 将与集合D中第i个法向量对应的关系记为ri∈R(1≤i≤k). 使用式(4)计算实体ej在ri对应超平面上的投影, 如图1所示.
| $ {{e}}_{j}^{i}={{e}}_{j}-{{d}}_{i}^{\text{T}}{{e}}_{j}{{d}}_{i} $ | (4) |
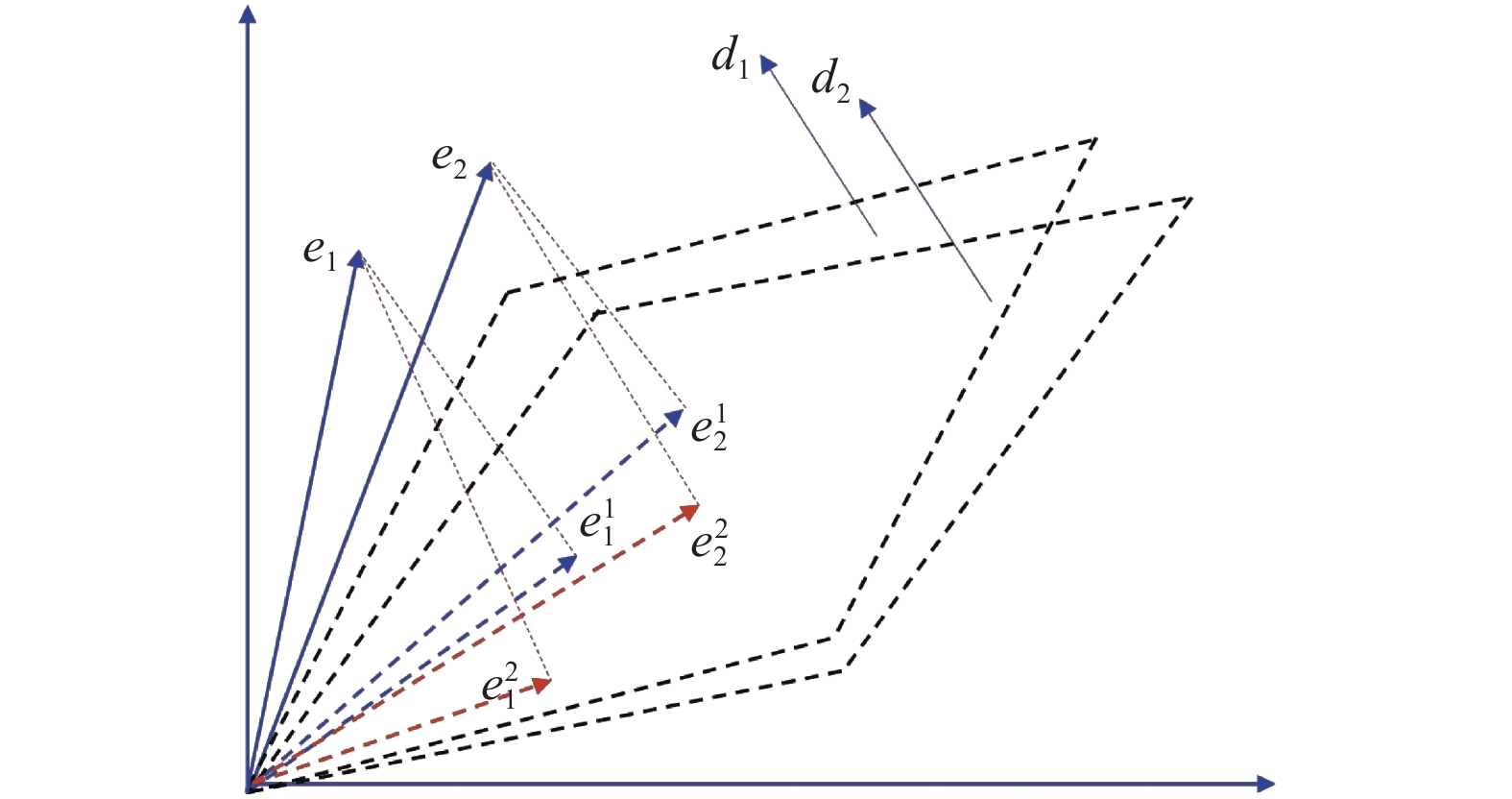
|
图 1 实体在各超平面中的投影 |
然后, 为了正确地在各超平面中搜索候选实体, 将每一个实体向量ej在超平面di (1≤i≤k)上的投影作为该实体在ri对应超平面中的语义表示, 并根据实体在不同超平面中的语义表示, 将具有共同语义特征的实体划分为一类. 具体而言, 由于K-means++算法[14]的效率高、能够高效地对海量实体进行划分[15], 因此, 通过投影向量间的余弦相似度表示对应实体在ri下的语义相似度, 使用K-means++对D中各超平面上的实体投影进行聚类, 将与
| $M({e_q}) = {M_1} \cap {M_2} \cap \cdots \cap {M_i} \cap \cdots \cap {M_k}$ | (5) |
其中, M(eq)表示候选实体搜索的结果.
算法1. 候选实体搜索算法
输入: eq: 给定的查询实体; Gkg: KG; S: 对eq影响最大的前k种关系集合
输出: M(eq): 候选实体集
1. 使用TransH将Gkg嵌入到向量空间中, 获得实体向量集E和与S对应的超平面法向量集D={d1, d2,…, dk}
2. for i=1 to k do
3. Ni←Ø
4. for each ej in E do
5.
6. 将
7. end for
8. K-means++(Ui) //对Ui中的实体投影进行聚类
9. 找到聚类结果中与
10. end for
11. M(eq)=M1∩M2∩…∩Mi∩ …∩Mk
12. return M(eq)
算法1主要的时间代价是在k个超平面中对实体投影进行聚类, 假设聚类类别数为n', 每一次聚类的时间复杂度为O(n'n)[14], 因此, 算法1的时间复杂度为O(kn'n).
3 相关实体排序模型 3.1 EUWG模型将需构造的无向带权图记为Geg, V是Geg中的节点, 由查询实体eq与候选实体组成, 使用V'表示V中除eq外的实体集合. 由于查询实体与各候选实体相关, 因此, 先在Geg中构造eq与V'各实体间的无向边, 然后, 通过计算各候选实体对应向量间的余弦相似度来构建候选实体间的无向边. 将V'中任意两实体记为vi和vj, 若vi和vj对应向量间的余弦相似度为正, 则在Geg中构造一条vi到vj的无向边, 表示vi与vj相关. 下面给出EUWG模型的定义:
定义2.
为了计算Geg中边上的权重, 并描述节点间的相关程度, 我们考虑以下两个方面:
(1) 向量相关度. 各实体在向量空间中的语义相关度决定其向量间的相关度, 使用实体向量间的余弦相似度来度量. 余弦相似度越高, 结构相关度越大. 计算方法如下:
| ${y_1}\left( {{{{v}}_i},{v_j}} \right) = {\textit{Sim}}\left( {{{{v}}_i},{{{v}}_j}} \right)$ | (6) |
其中, Sim(·)表示实体向量间的余弦相似度.
(2) Web文档相关度, 即Geg中任意两个节点在Web文档中共现频率反映的相关度[3]. 我们统计
| ${y_2}\left( {{{{v}}_i},{v_j}} \right) = \sum\limits_{x = 1}^c {g({h_x},{{{v}}_i},{{{v}}_j})} $ | (7) |
其中, 若实体vi与vj共同出现在hx (1≤x≤c)中, 则g (hx, vi, vj)为1, 否则为0.
使用超参数β来平衡上述因素对Geg边上权重的贡献. 为了统一y1(vi, vj)和y2(vi, vj)的取值区间, 使用最大最小归一化函数对其进行处理:
| $w\left( {{v_i},{v_j}} \right) = \beta Nor\left( {{y_1}\left( {{{{v}}_i},{v_j}} \right)} \right) + \left( {1 - \beta } \right)Nor\left( {{y_2}\left( {{{{v}}_i},{v_j}} \right)} \right)$ | (8) |
Geg中任意两个节点间有多条路径, 不同的路径决定了节点间不同的相关程度. 因此, 通过获取查询实体eq与候选实体vi∈V'在Geg中的所有路径来计算每条路径上权重的平均值, 将其中的最大值作为候选实体vi的分数, 并基于该分数对候选实体进行排序, 计算方法如下:
| ${\textit{Score}}({e_i}) = \text{max}\left( {\frac{{\displaystyle\sum\limits_{a = 1}^{\left| {{{\textit{z}}_j}} \right| - 1} {w\left( {{\textit{z}}_j^a,{\textit{z}}_j^{a + 1}} \right)} }}{{\left| {{{\textit{z}}_j}} \right|}}} \right), \; j=1,2,\cdots,\left| {{Z_i}} \right|$ | (9) |
其中, Zi表示查询实体eq到候选实体vi所有的路径集合, zj表示第j条路径需要经历的所有实体集合,
算法2. 基于EUWG模型的候选实体排序
输入: eq: 给定的查询实体; V: 候选实体集M(eq)与查询实体eq的并集; L: Geg中边的集合
输出: B: 实体排序结果
1. i←1, j←1, tmp_B←Ø, B←Ø
2. for each v in V–{eq} do
3. Z←BFS(L, e, eq) //使用广度优先算法获取Geg中实体eq到v的所有路径
4. score←0
5. for each z in Zdo
6. weight←0
7. for a=0 to |z|–1 do
8. weight←weight+w(za, za+1)
9. end for
10. if weight/|z|>score then //将各路径权重平均值的最大值作为候选实体分数
11. score←weight/|z|
12. end for
13. tmp_B←tmp_B∪{(v, score)} //tmp_B保存候选实体v及其分数score组成的二元组(v, score)
14. end for
15. 根据tmp_B中候选实体的分数, 对实体进行排序, 将排序结果保存在B中
16. return B
在算法2中, 假设Geg的节点数为s, 算法主要的时间代价是对s–1个候选实体进行广度优先搜索,
(1) 数据集与测试环境
为了测试本文提出方法的效果, 使用Wikidata (
| 表 1 测试数据集 |
| 表 2 验证数据集 |
| 表 3 Web文档数据集 |
实验使用E5-2650v3 2.3 GHz处理器, 2080Ti GPU, 128 GB内存, 用Python作为编程语言, 并使用Spark和TensorFlow框架作为编程框架.
(2) 测试指标
使用准确率(Precision, P)、召回率(Recall, R)以及F1分值来评价算法1的有效性, 计算方法如下:
| $ {{P}} = \frac{{TP}}{{TP + FP}}, \;\quad {{R}} = \frac{{TP}}{{TP + FN}}, \; \quad F1=\frac{2\times P\times R}{P+R} $ | (10) |
其中, TP为被正确搜索到的候选实体数, FP为被错误搜索到的候选实体数, FN为未被搜索到的候选实体数.
为了验证EUWG模型的有效性, 使用皮尔逊相关系数(Pearson Correlation Coefficient, PCC)、斯皮尔曼等级相关系数(Spearman Correlation Rank Coefficient, SCRC)以及调和均值(Harmonic Mean, HM)来评价排序结果. 其中PCC表示测试结果与验证数据集中相关度分数的一致性, SCRC表示测试结果与验证数据集实体排序的一致性, HM表示测试结果与验证数据集之间的综合一致性. 计算方法如下:
| $PCC = \dfrac{{\displaystyle\sum {\left( {X - \dfrac{X}{{AC}}} \right)\left( {Y - \dfrac{Y}{{AC}}} \right)} }}{{\sqrt {\displaystyle\sum {{{\left( {X - \dfrac{X}{{AC}}} \right)}^2}} } \sqrt {\displaystyle\sum {{{\left( {Y - \dfrac{Y}{{AC}}} \right)}^2}} } }}$ | (11) |
| $SCRC = 1 - \frac{{6\displaystyle\sum\limits_{i = 1}^{AC} {b_i^2} }}{{AC\left( {A{C^2} - 1} \right)}}$ | (12) |
| $HM = \frac{{2 \times PCC \times {\textit{SCRC}}}}{{{{PCC}} + {\textit{SCRC}}}}$ | (13) |
其中, X为测试结果中的候选实体分数集, Y为验证数据集中各候选实体的分数集, AC为候选实体数, bi为第i个实体在测试结果中的位置与验证数据集中位置的差值, PCC、SCRC和HM的值越接近1, 说明结果越好.
4.2 候选实体搜索有效性测试为了测试实体数量对算法1的影响, 分别在KORE与ERT上测试了候选实体搜索的准确率、召回率和F1值, 如图2所示. 可以看出, 随着实体数量的增加, 各项指标都有所下降. 当实体数量从1×105增加到5×105时, 实体数量增加了5倍, 但召回率仅降低了10%. 原因在于, 实体数量的增加使得TransH的学习结果更加准确, 并能够更有效地表示实体的语义, 进而使算法1在大规模的KG上也表现优异.
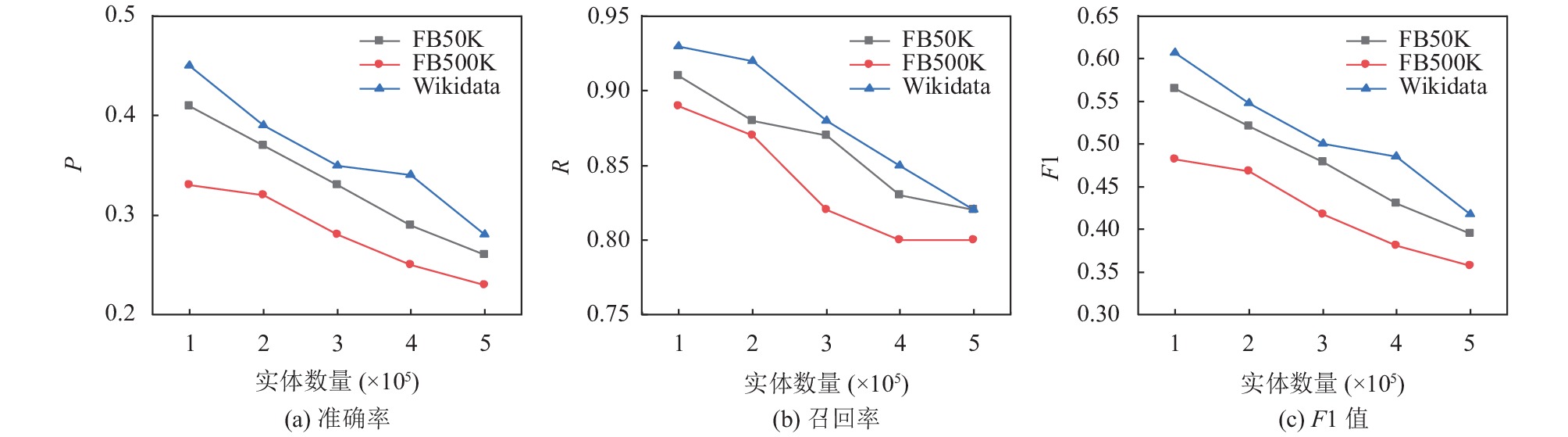
|
图 2 实体数对候选实体搜索的影响 |
然后, 测试了不同聚类类别数对算法1的影响. 在各KG中选择5×105个实体, 取不同的聚类类别数进行测试, 如图3所示. 可以看出, 随着聚类数的增加, 准确率和F1值都有所上升, 原因在于类别数越多, 候选实体集中被错误召回的实体数量所占的比例越小, 进而候选实体搜索的准确性就越高.
另外, 将本文提出的候选实体搜索算法记为TCES(TransH-based Candidate Entity Search), 从各KG中选择5×105个实体, 设置聚类类别数为170, 与REFH[4]和LTRC[5]算法进行对比, 如表4所示. 可以看出, 算法1在FB50K和FB500K数据集上效果更好, 且在Wikidata上准确率和F1值也高于其他两种方法. 原因在于, 算法1从KG所有实体中寻找候选实体, 搜索范围更大, 进而被正确召回的实体数目更多.

|
图 3 聚类类别数对候选实体搜索的影响 |
4.3 EUWG模型有效性测试
为了测试KG规模对候选实体排序的影响, 选择4.5×105个Web文档, 测试算法2在不同三元组数量下的PCC、SCRC和HM, 如图4所示. 可以看出, 随着三元组数量增加, PCC、SCRC和HM都有所上升. 当三元组数量达到5×106时, 各指标平均增加了29%、17%和25%. 原因在于随着三元组数量的增加, KG中蕴含的知识更加完整, TransH能够更有效地对KG进行表示, 使得EUWG模型中向量相关度的计算更加准确, 进而排序效果有所提升.
另外, 为了测试不同Web文档数对相关实体排序的影响, 从各KG中分别选择5×106个三元组, 测试算法2在不同Web文档数下的PCC,SCRC和HM, 如图5所示. 可以看出, 随着Web文档数增加, 各指标也随之上升, 当数据量为4.5×105时, 各指标平均提升了41%、30%和34%. 原因在于随着Web文档数的增加, 其中的知识也随之增加, 对实体相关性的描述信息也更加丰富, 使得EUWG模型对实体在Web文档中相关性的量化更加准确, 进而提升了排序效果.
| 表 4 不同KG的候选实体搜索结果 |

|
图 4 KG规模对候选实体排序的影响 |
最后, 我们从KG中分别选择5×106个三元组, 并使用4.5×105个Web文档和不同领域的查询实体进行测试, 与WLM[8]、TSF[9]和Wikipedia2Vec[12]模型进行比较, 如图6和图7所示. 可以看出, 本文提出的EUWG模型在实体排序任务中表现较好, 其中, EUWG模型比其他3种方法的PCC高了18%. 原因在于Wikipedia2Vec模型在将KG映射为向量时会发生实体和词汇的匹配错误. 同时, WLM与TSF模型主要根据KG来计算实体间的相关度, 但KG无法及时地反映真实世界不断演化的知识, 因此计算结果不够准确, 而EUWG使用Web文档和KG共同描述实体间的相关关系, 使得计算结果更加客观, 进而候选实体的排序结果更好.
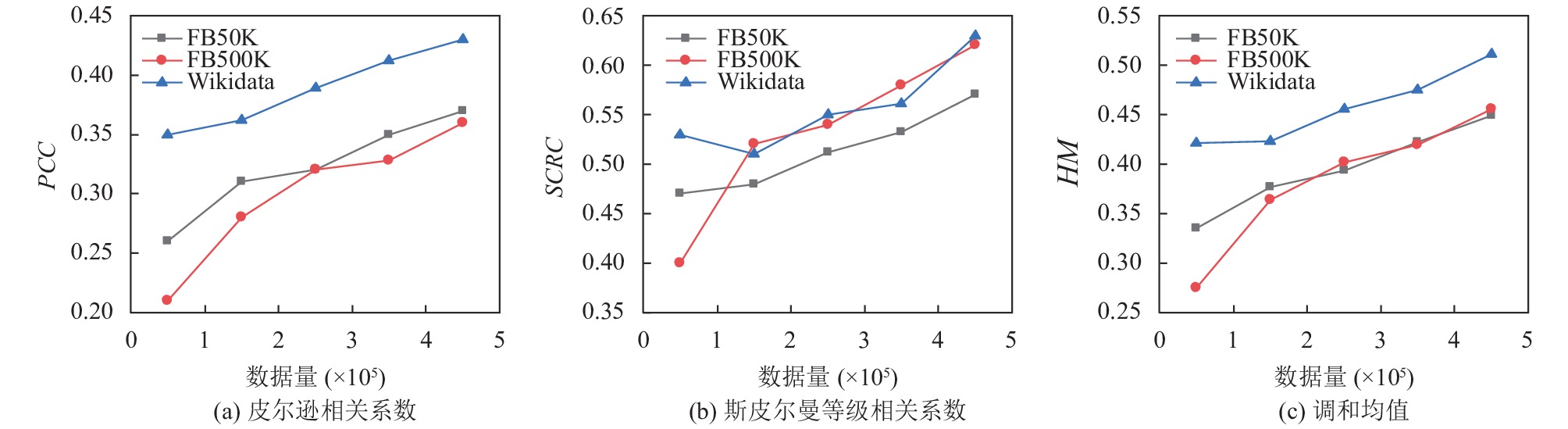
|
图 5 Web文档数对候选实体排序的影响 |

|
图 6 基于FB50K的候选实体排序结果 |

|
图 7 基于FB500K的候选实体排序结果 |
5 结束语
本文提出了基于表示学习的相关实体搜索算法, 通过对向量空间中不同关系超平面上的实体投影进行聚类, 获得与查询实体相关的候选实体, 并使用实体带权无向图模型对候选实体进行排序. 实验结果表明, 本文提出的方法能够正确地从KG中搜索候选实体, 同时有效地对候选实体进行排序. 但在候选实体排序任务中使用的数据源仍有待进一步扩展. 因此, 在未来工作中考虑加入Web应用中与实体相关的图片数据, 更加客观全面地描述实体间的关系信息, 提高相关实体搜索的准确性.
| [1] |
黄恒琪, 于娟, 廖晓, 等. 知识图谱研究综述. 计算机系统应用, 2019, 28(6): 1-12. DOI:10.15888/j.cnki.csa.006915 |
| [2] |
张香玲, 陈跃国, 马登豪, 等. 实体搜索综述. 软件学报, 2017, 28(6): 1584-1605. DOI:10.13328/j.cnki.jos.005256 |
| [3] |
Rahman MM, Takasu A, Demartini G. Representation learning for entity type ranking. Proceedings of the 35th Annual ACM Symposium on Applied Computing. New York: ACM, 2020. 2049–2056.
|
| [4] |
Reinanda E, Meij E, Pantony J, et al. Related entity finding on highly-heterogeneous knowledge graphs. Proceedings of 2018 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. Barcelona: IEEE, 2018. 330–334.
|
| [5] |
Huang JZ, Ding SQ, Wang HF, et al. Learning to recommend related entities with serendipity for web search users. ACM Transactions on Asian and Low-Resource Language Information Processing, 2018, 17(3): 25. DOI:10.1145/3185663 |
| [6] |
祁志卫, 王笳辉, 岳昆, 等. 图嵌入方法与应用: 研究综述. 电子学报, 2020, 48(4): 808-818. DOI:10.3969/j.issn.0372-2112.2020.04.023 |
| [7] |
Wang Z, Zhang JW, Feng JL, et al. Knowledge graph embedding by translating on hyperplanes. Proceedings of the 28th AAAI Conference on Artificial Intelligence. Quebec City: ACM, 2014. 1112–1119.
|
| [8] |
Milne D, Witten IH. An effective, low-cost measure of semantic relatedness obtained from wikipedia links. Proceedings of 2008 AAAI Workshop on Wikipedia and Artificial Intelligence: An Evolving Synergy. Chicago: AAAI, 2008. 25–30.
|
| [9] |
Ponza M, Ferragina P, Chakrabarti S. On computing entity relatedness in wikipedia, with applications. Knowledge-Based Systems, 2020, 188: 105051. DOI:10.1016/j.knosys.2019.105051 |
| [10] |
Rothe S, Schütze H. CoSimRank: A flexible & efficient graph-theoretic similarity measure. Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics. Baltimore: Association for Computational Linguistics, 2014. 1392–1402.
|
| [11] |
Qian JW, Li XY, Zhang CH, et al. Social network de-anonymization and privacy inference with knowledge graph model. IEEE Transactions on Dependable and Secure Computing, 2019, 16(4): 679-692. DOI:10.1109/TDSC.2017.2697854 |
| [12] |
Yamada I, Shindo H, Takeda H, et al. Joint learning of the embedding of words and entities for named entity disambiguation. Proceedings of the 20th SIGNLL Conference on Computational Natural Language Learning. Berlin: Association for Computational Linguistics, 2016. 250–259.
|
| [13] |
Wikipedia. Feature scaling. https://en.wikipedia.org/wiki/Feature_scaling. [2021-07-02].
|
| [14] |
Arthur D, Vassilvitskii S. K-means++: The advantages of careful seeding. Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms. New Orleans: ACM, 2007. 1027–1035.
|
| [15] |
LeLand M, John H. Benchmarking performance and scaling of Python clustering algorithms. https://hdbscan.readthedocs.io/en/latest/performance_and_scalability.html. [2021-08-30].
|
| [16] |
Hoffart J, Seufert S, Nguyen DB, et al. KORE: Keyphrase overlap relatedness for entity disambiguation. Proceedings of the 21st ACM International Conference on Information and Knowledge Management. Maui: ACM, 2012. 545–554.
|
| [17] |
Herrera JET, Casanova MA, Nunes BP, et al. An entity relatedness test dataset. Proceedings of the 16th International Semantic Web Conference on the Semantic Web. Vienna: Springer, 2017. 193–201.
|
 2021, Vol. 30
2021, Vol. 30



