人员排班问题[1]是指在一定周期内将工作安排给合适的员工完成, 安排的过程中通常涉及一系列国家法律法规以及公司规章制度, 证实是一个NP难问题[2]. Ernst等[3]提出典型人员排班问题通常涉需求模型、休息日计划、班次计划、人员分配等几大模块. 在地勤人员的排班问题中[4], 由于飞机起降的不确定性经常造成延误, 通常还涉及重新规划(Stolletz[5]). 本文描述了航空物流服务公司出港操作室的劳动力规划过程, 重点在员工每个月的行程安排, 在这个问题中, 班次不是固定的[6], 而是基于任务特点推导而成, 任务分配过程涉及员工班次和休息日安排, 并且考虑重新规划成本.
目前人员排班不再限于关注硬性人员雇佣成本, 还考虑未来发展, 宁愿付出相当代价增加对人员公平[7]和个人偏好[8, 9]方面的重视以提高士气. 本文在面向多技能员工排班[10]前提下, 考虑员工班在次间的任务数量、工作强度等因素的公平和均衡.
在劳动密集型行业或者用人高峰季节通常会出现人员紧缺现象, 因此任务覆盖率是衡量排班质量的一项重要标准, 现有文献多采用聘用外部雇员、临时工、加班等方式来填补缺口. 许丹等人[11]探索了人力资源不足情景下的护士排班加班策略, 并设计一种遗传算法对模型进行求解. 胡修武等人[12]考虑可加班的呼叫中心人员排班问题, 并采用邻域搜索算法进行求解. Maenhout等人[13]采用聘请外部临时工的方式解决人员需求缺口, 并基于分散搜索算法模型进行求解. Stolletz等人[14]通过动态加班补偿机制和聘请外部医生两种方法结合来弥补需求覆盖缺口, 并对使用分解启发式算法、混合整数规划和集合覆盖模型求解的效果进行对比.
然而, 这种选择应用在航空业上不仅带来了直接的高昂的成本, 由于航空公司任务时间与航班时刻挂钩, 每日航班起降高峰出现用人高峰, 短期峰值后用人量减少, 闲置人员增加, 无疑也间接造成成本浪费. 再者, 航空作为受天气等不确定因素影响的行业, 经常会出现航班延误、取消等不可控突发情况, 无法立刻从外部雇佣合格的临时员工. 为解决这个问题, 本文倾向于在前期排班时适当舍弃部分任务, 这部分任务可由现场调度人员根据实际情况调度员工完成. 若仅以总体覆盖率最大化为目标, 可能造成每天的覆盖率不均衡的情况, 导致有些天无法覆盖的任务过多, 无法使用现场调度进行弥补. 因此在模型中, 尽可能保障无法覆盖的任务均摊至能被当天值班人员兼顾, 如通过加快速度缩短任务完成时间等方法. 从管理的角度出发, 人员排班要求做到均衡任务覆盖, 同时根据最终的解决方案的无法覆盖任务数量以及在各时间段的分布情况, 可供分析缺人性质是整体人员不足还是高峰用人呈现临时性缺人, 协助管理层对人员组成进行决策和调整.
本文提出了一种基于变邻域搜索算法的模型求解策略, 它能够很好地跳出局部最优, 并具有良好的时效性.
本文的主要贡献如下: (1)基于任务特点生成非固定时段的多岗位均衡任务班次; (2)建立均衡任务覆盖率的混合整数规划模型; (3)对航空物流服务公司出港操作室的真实数据进行测试, 证明方法在管理上行之有效.
1 问题描述航空物流服务公司出港操作室的主要任务为将客户的货物从接收到送上货机的整个过程涉及的工作和程序, 共涉及6个岗位: 接单岗、操作岗、复核岗、过磅岗、拉货岗、夜班岗.
人员排班分为两个阶段: 第1阶段为班次生成[15], 即指将根据相关法律法规将任务打包成班次以覆盖总任务计划中的所有任务; 第2阶段班次分配[16], 即将生成的班次按照一定的规则分配给员工.
本文考虑以一个月为周期的排班问题, 这个问题包括将拥有一种或多种岗位资质的员工, 安排到排班周期内的班次中. 由任务岗位性质可知, 不同任务间持续时间相差较大, 为均衡班次的任务数量和员工工作强度, 引入一个新的概念:
定义1. 长任务. 任务持续时间超过1 h的任务称为长任务, 其余为普通任务.
任务持续时长影响员工工作满意度, 同岗位班次中长任务过少导致频繁切换任务, 且任务总数量上多于其他班次会造成员工内心的不公平感, 因此均衡班次长任务数量是公平的重要体现. 本文希望做到在遵循所有合同制约的前提下, 满足员工之间的公平性原则, 对班次的任务个数、长任务个数等尽可能平均. 同时在排班周期内按天均衡任务覆盖率, 即在人员不足的前提下, 无法覆盖的任务在排班周期内呈现日均衡, 以确保可以通过现场调度解决高峰时期人员稀缺问题.
2 模型建立模型建立分为两个阶段, 分别为班次生成和班次分配阶段. 本文用大写字母表示输入的数据、已知参数和可以静态计算的量, 小写字母表示决策变量、未知参数与下标, 用上标表示为标签而不是指数运算, |∙|表示集合元素个数.
2.1 班次生成冯霞等人[17, 18]研究了层次资质下的班次生成问题, 本文结合航空物流服务公司出港操作室的实际情况, 提出多种岗位下的班次生成模型[19]. 整数规划模型符号如表1、表2所示.
| 表 1 班次生成集合符号 |
| 表 2 班次生成参数符号 |
中心决策变量为是否将任务
| $ a_{st} = \left\{ \begin{array}{l} 1,\;{\text{将任务}}t{\text{分配给班次}}s\\ 0,\;{\text{否则}} \end{array} \right.\;\; $ |
其他决策变量有:
| $ \mathop {{l}}\nolimits_{sq} = \left\{ \begin{array}{l} 1,\;{\text{班次}}{{s}}{\text{的岗位为}}{{q}}\\ 0,\;{\text{否则}} \end{array} \right.\;\; $ |
定义“\”表示两个集合的相对差集, 则班次生成模型如下:
| $ \min {\textit{z}}e \sum\limits_{{{s}} \in S} {\left( {\mathop e\nolimits_s^S - \mathop s\nolimits_s^S } \right)} \;$ | (1) |
| $\sum\limits_{s \in S} {\mathop a\nolimits_{st} = 1,\forall t \in T} $ | (2) |
| $\mathop a\nolimits_{si} \cdot \mathop E\nolimits_{{i}}^T - \mathop a\nolimits_{sj} \cdot \mathop S\nolimits_j^T \ge \mathop B\nolimits^{lb} ,\forall s \in S,\forall i,j \in T,i \ne j$ | (3) |
| $\sum\limits_{{{t}} \in T} {\mathop a\nolimits_{st} \cdot \mathop K\nolimits_{tq} \le M \cdot \mathop l\nolimits_{sq} ,\forall s \in S,\forall {{q}} \in Q} $ | (4) |
| $\sum\limits_{q \in Q} {\mathop l\nolimits_{sq} \le 1,\forall s \in S,\forall {{s}} \in S} $ | (5) |
| $\mathop L\nolimits^{lb} \le \mathop e\nolimits_s^S - \mathop s\nolimits_s^S \le \mathop L\nolimits^{ub} ,\forall s \in S\backslash \mathop s\nolimits_1^Q $ | (6) |
| $\mathop L\nolimits^{lb} \le \mathop e\nolimits_s^S - \mathop s\nolimits_s^S \le \mathop L\nolimits^{Nub} ,\forall s \in \mathop s\nolimits_1^Q $ | (7) |
其中, 班次生成目标函数(1)表示最小化班次时间, 约束(2)表示每个任务必须分配到一个班次, 约束(3)表示表示同一班次内任务间隔时间不小于
整数规划模型的符号表示如表3、表4所示, 中心决策变量为是否将第
| $ \mathop x\nolimits_{esd} = \left\{ \begin{array}{l} 1\;,\;\;{\text{第}}{{d}}{\text{天的班次分配给员工}}{{e}}\\ 0\;,\;\;{\text{否则}} \end{array} \right.\;\; $ |
其他决策变量为:
| $ \begin{array}{l} \mathop {{u}}\nolimits_s = \left\{ \begin{array}{l} 1\;,\;\;{{{\text{班次}}s{\text{未被分配}}}}\\ 0\;,\;\;{\text{否则}} \end{array} \right.\;\;\\ \mathop {{y}}\nolimits_{ed} = \left\{ \begin{array}{l} 1\;,\;\;{\text{员工}}{{e}}{\text{在第}}{{d}}{\text{天上班}}\\ 0\;,\;\;{\text{否则}} \end{array} \right.\;\; \end{array} $ |
| 表 3 班次分配集合符号 |
| 表 4 班次分配参数符号 |
班次分配整数规划模型的目标函数(8)是最小化未完成任务的总工时, 保障最大任务覆盖率. 具体模型如下:
| $\min {\textit{z}}e \sum\limits_{{{s}} \in S} {\mathop {{u}}\nolimits_s \cdot \mathop I\nolimits_{st} \cdot \left( {\mathop e\nolimits_{{t}}^T - \mathop s\nolimits_{{t}}^T } \right)} \;$ | (8) |
| $\mathop u\nolimits_s + \sum\limits_{e \in \mathop E\nolimits_s } {\mathop x\nolimits_{esd} = 1,\forall s \in S} $ | (9) |
| $\sum\limits_{s \in S} {\mathop x\nolimits_{esd} - \mathop y\nolimits_{ed} = 0,\forall e \in E,\forall {{d}} \in D} $ | (10) |
| $\mathop H\nolimits^{lb} \le \sum\limits_{{{d}} \in D} {\sum\limits_{s \in S} {\mathop {{x}}\nolimits_{esd} \cdot \left( {\mathop e\nolimits_s^S - \mathop {{s}}\nolimits_s^S } \right) \le \mathop H\nolimits^{ub} ,\forall e \in E} } $ | (11) |
| $\begin{split} & \mathop x\nolimits_{eid} + \mathop x\nolimits_{ej\left( {d + 1} \right)} - \mathop C\nolimits_{ij} \le 1,\forall e \in E,\forall s \in S, \\ & \forall d \in D,\forall i \in \mathop S\nolimits_d^D ,\forall j \in \mathop S\nolimits_{d + 1}^D ,i \ne j \end{split} $ | (12) |
| $7 - \sum\limits_{d \in \mathop D\nolimits_w } {\mathop y\nolimits_{ed} \le \mathop R\nolimits^{Wub} ,\forall e \in E,\forall w \in W} $ | (13) |
| $7 - \sum\limits_{d \in \mathop D\nolimits_w } {\mathop y\nolimits_{ed} \ge \mathop R\nolimits^{Wlb} ,\forall e \in E,\forall w \in W} $ | (14) |
| $\left| D \right| - \sum\limits_{d \in D} {\mathop y\nolimits_{ed} \le \mathop R\nolimits^{Mub} ,\forall e \in E} $ | (15) |
| $\left| D \right| - \sum\limits_{d \in D} {\mathop y\nolimits_{ed} \ge \mathop R\nolimits^{M{{l}}b} ,\forall e \in E} $ | (16) |
| $\begin{split} &\left( {\mathop {2 - x}\nolimits_{eid} + \mathop x\nolimits_{ej\left( {d + 1} \right)} } \right) \cdot M \ge \mathop y\nolimits_{e\left( {{{d}} + 2} \right)} + \mathop y\nolimits_{e\left( {{{d}} + 3} \right)} , \\ & \forall e \in E,\forall i,j \in \mathop S\nolimits_1^Q ,i \ne j \end{split} $ | (17) |
约束(9)表示如果班次
从管理的角度出发, 本文考虑的均衡性主要包括两个方面: 一是基于班次之间工作量的均衡性, 即使得每个班次间总任务数量以及长任务数量尽可能平均, 保障分配到不同班次的员工所做任务数量均衡; 二是基于每日完成任务覆盖率的均衡, 保障员工间工作强度的均衡.
本文将采用在原优化目标中加上一定权重下的均衡优化目标或者在原约束条件中加上均衡约束的方法来限制优化目标.
3.1 基于班次间的均衡根据对航空物流服务公司出港操作室的访谈, 得出该部门班次间的均衡主要体现在班次间总任务和长任务数量的均衡. 假设
| $Minimi{\textit{z}}e \; g(s) = \sum\limits_{{{s}} \in S} {\mathop {\alpha \left( {\mathop {{n}}\nolimits^{ub} - \mathop {{n}}\nolimits^{lb} } \right){{ + }}\beta \left( {\mathop {{n}}\nolimits^{Lub} - \mathop {{n}}\nolimits^{Llb} } \right)}\nolimits_{} } $ | (18) |
| $\mathop n\nolimits^{lb} \le \sum\limits_{t \in T} {\mathop a\nolimits_{st} \le \mathop n\nolimits^{ub} ,\forall s \in S} $ | (19) |
| $\mathop n\nolimits^{Llb} \le \sum\limits_{t \in T} {\mathop a\nolimits_{st} \le \mathop n\nolimits^{Lub} ,\forall s \in S} $ | (20) |
基于班次间均衡的目标函数式(18)是小化班次间总任务和长任务数量差异. 约束(19)表示班次
假设
| $\mathop M\nolimits^{\rm{ava}} = \left( {\left| D \right| - \mathop R\nolimits^{Mlb} } \right) \times \left| E \right| - \mathop M\nolimits^{\rm{pre}} $ | (21) |
| $\mathop M\nolimits_d^{\rm{ava}} = \left( {\frac{{\mathop M\nolimits^{\rm{ava}} }}{{\left| S \right|}}} \right) \times \left| {\mathop S\nolimits_d^D } \right|$ | (22) |
式(21)计算周期内的可用人力, 其中
如果
| $\sum\limits_{e \in \mathop E\nolimits_{{s}} } {\sum\limits_{s \in \mathop S\nolimits_d^D } {\mathop {{x}}\nolimits_{esd} \le \mathop M\nolimits_d^{\rm{ava}} ,\forall d \in D} } $ | (23) |
在班次生成阶段, 先用贪婪算法构造初始解, 然后选择变邻域搜索算法对班次生成方案进行调整, 采用任务交换、任务插入、任务交叉3种邻域结构分别如图1、图2、图3所示. 班次分配阶段选用符合第2.2节分配约束和第3节均衡策略进行分配.

|
图 1 任务交换过程 |
4.1 班次生成 4.1.1 初始解生成
班次生成的初始解步骤如下:
Step 1. 将集合
Step 2. 从第1个任务开始遍历, 将任务
Step 3. 寻找满足约束(3)–约束(7)的任务加入到班次
Step 4. 遍历未分配班次的任务, 取第1个作为新班次的第1个任务, 重复Step 2–Step 3. 当满足约束(2)时, 得到所有班次初始解, 否则转到Step 4.
4.1.2 邻域结构设置邻域结构的设计是变邻域搜索算法的核心, 在保障解的可行性前提下进行领域动作, 生成可行的候选解. 本节设计了3种邻域结构来生成候选解: 任务交换、任务插入、任务交叉, 分别设为
(1)任务交换方法
从候选解中随机选择两个班次
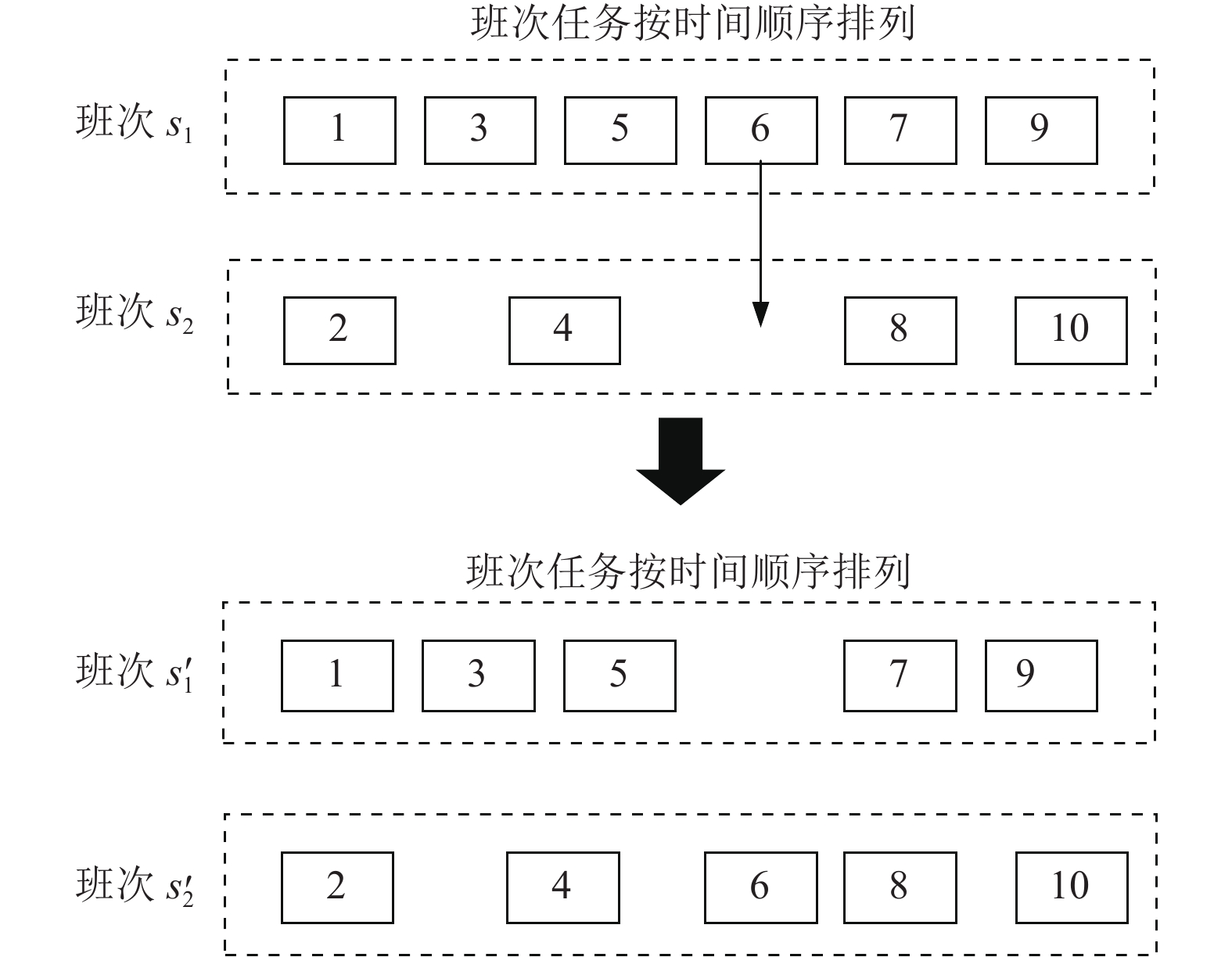
|
图 2 任务插入过程 |
|
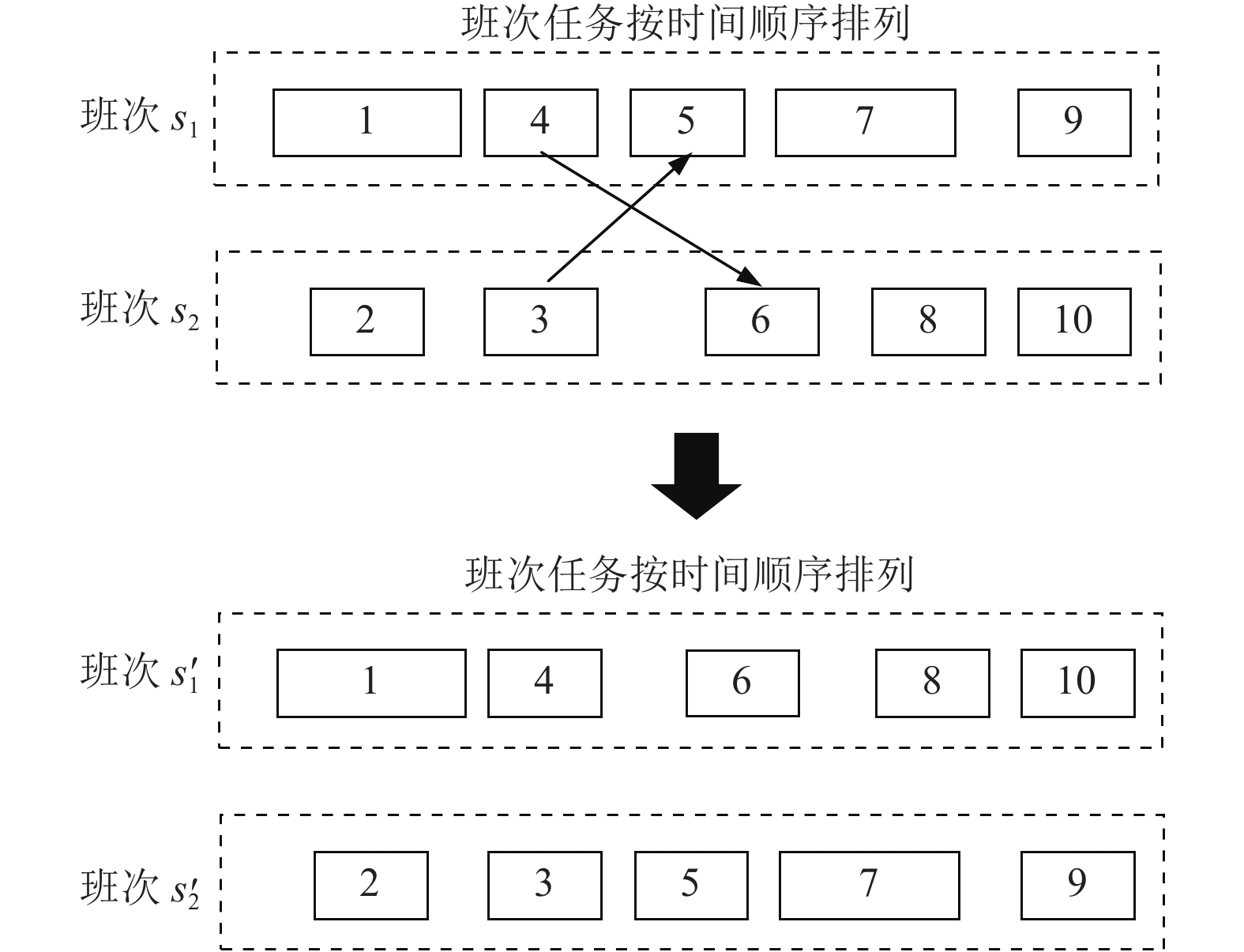
图 3 任务交叉过程 |
(2)任务插入方法
从候选解中随机选择两个班次
(3)任务交叉方法
从候选解中随机选择两个班次
变邻域搜索算法利用4.1.2节的3种邻域结构进行搜索, 整个算法过程只接受可行解. 每进行一次邻域动作就对新生成的解进行评估, 评估函数为3.1节的目标函数
4.2 班次分配
为方便求解, 引入以下定义:
定义2. 候选人. 如果员工
定义3. 不可指派班次. 由于候选人不足或控制班次数等原因造成不能指派给员工完成的班次.
Step 1. 将集合
Step 2. 取第一个班次
Step 3. 在Step 2后, 如果剩余的候选人不为空, 则选取当前月工时最短的候选人e. 否则将班次加入到不可指派班次中.
Step 4. 判断是否满足
Step 5. 重复Step 2–Step 4, 直到所有班次分配完毕, 算法结束.
5 数值实验 5.1 实验数据数值实验选取航空物流服务公司出港操作室2019年11月份数据, 包括64名员工、6种岗位. 总任务个数为7893个, 操作岗任务为7161个. 表5显示了具体任务信息, 可以看出除了操作岗其余各岗位时长均超过7小时, 即一个任务为一个班次, 而操作岗时长较短, 一个班次往往包含多个任务, 因此第4.1节的任务移动操作主要针对操作岗.
| 表 5 任务信息表 |
5.2 实验设置
本文采用Java实现第4节算法, 实验使用的硬件环境为Intel(R) Core(TM) i7-8550U CPU @1.80 GHz主频, 内存为8 GB的计算机. 班次生成算法设置最大迭代次数
| 表 6 实验参数设置 |
5.3 实验结果
实验共生成班次1524个, 班次生成方案的信息包括班次日期、班次编号、班次起始时间、班次岗位资质、以及班次保障任务集等, 具体实验结果如表7所示.
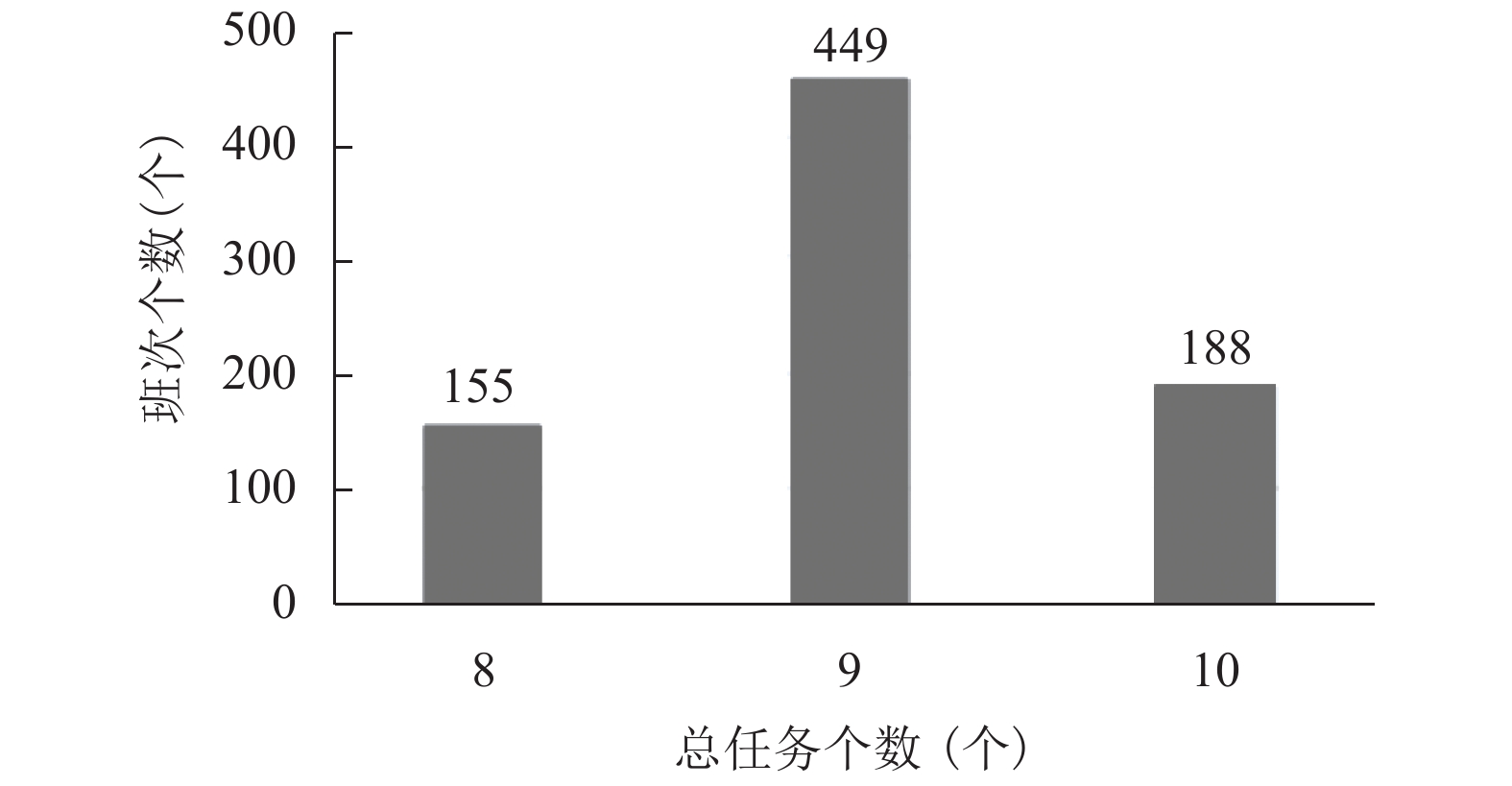
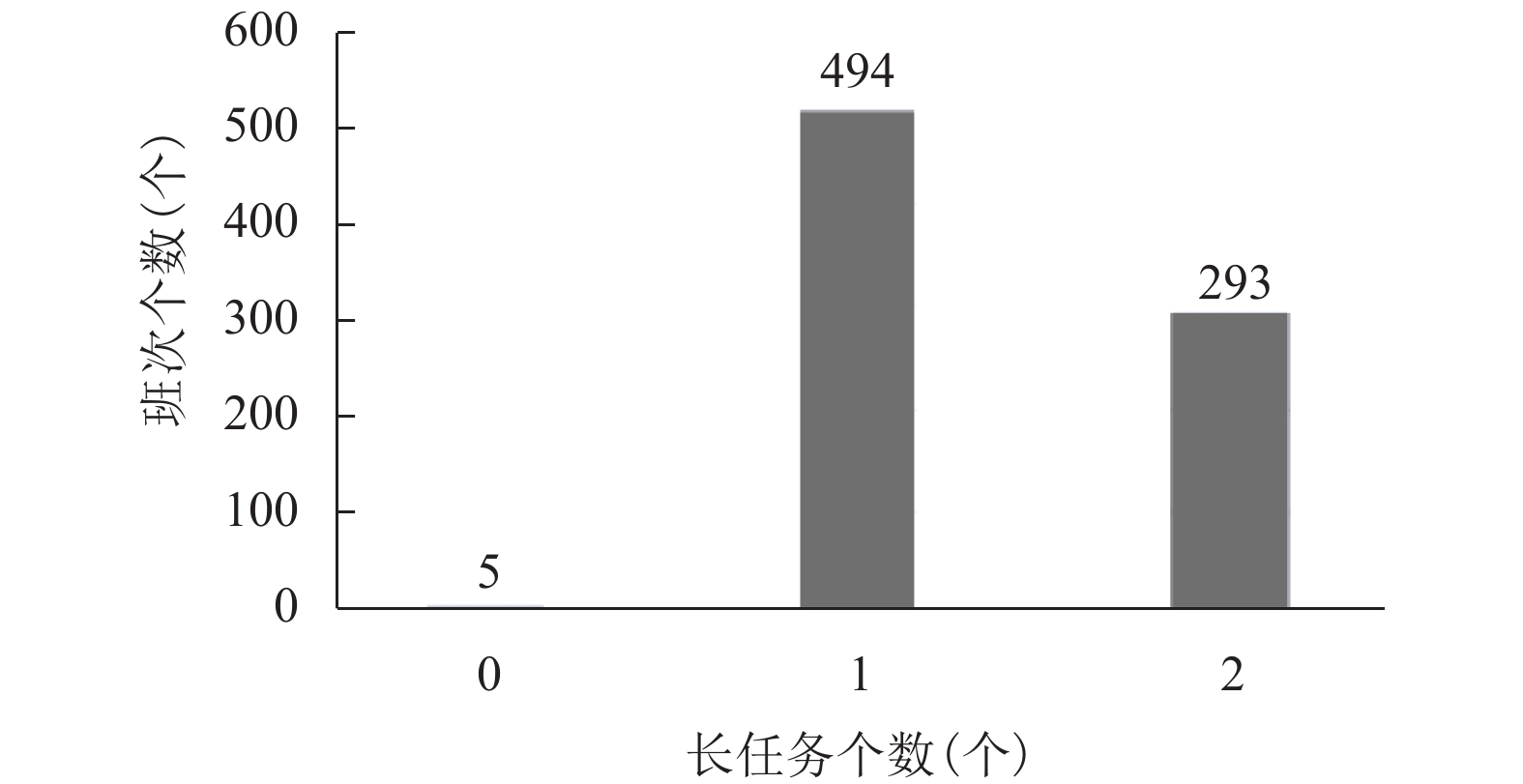
其中, 生成的操作岗班次由多个保障任务构成, 由第3节可知为了保障同岗位资质的班次间的工作强度一致, 尽可能保障同类班次间的总任务数以及长任务数的数量平均. 图4和图5分别表示在班次生成阶段2019年11月操作岗班次的中总任务数量和长任务数量的个数.
| 表 7 班次生成实验结果 |
由上述实验数据可知, 一个操作岗班次总任务大多集中在9个左右, 其余都在与平均总任务个数相差1个任务幅度范围内, 每个班次长任务个数集中在1个到2个, 整体上呈现均衡. 根据航班数据显示, 航班存在比较明显的起降高峰, 在航班起降低峰期班次内任务数量较少, 起降高峰班次内任务数量较多是不可避免的, 因而总体的班次生成方案设置合理, 在工作量以及工作强度上呈现均衡性.
在班次分配阶段, 由
|
图 4 操作岗班次总任务个数分布 |
|
图 5 操作岗班次长任务个数分布 |
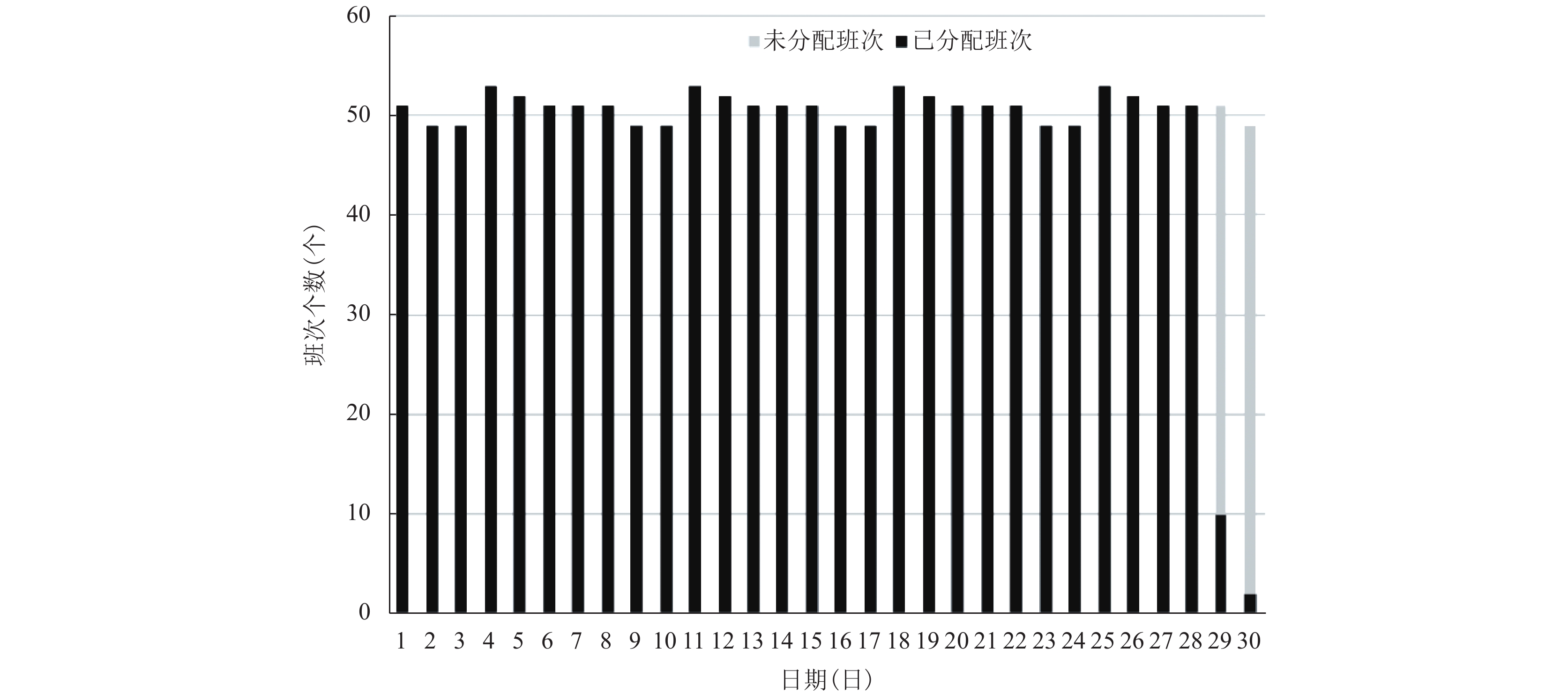
|
图 6 均衡前月度班次分配情况 (2019年11月) |
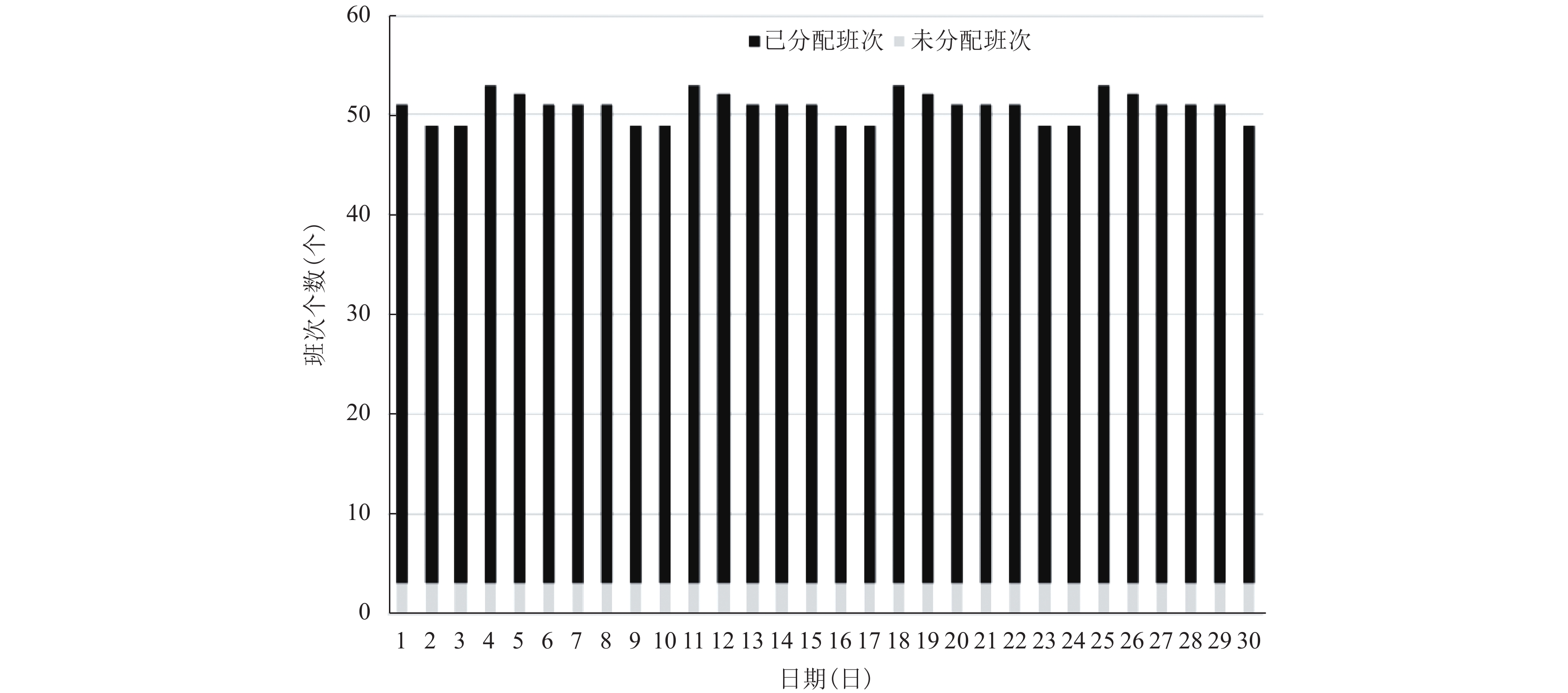
|
图 7 均衡后月度班次分配情况 (2019年11月) |
6 结论
本文在结合国内外机场地勤人员排班研究的基础上, 调研航空物流服务公司出港操作室的具体业务场景, 建立了一套均衡任务覆盖率模型. 数值实验表明这个模型对航空业或受季节、突发事件影响大而导致的缺人的情况下更有效. 均衡任务覆盖模型可以很好应对不确定性, 给现场调度人员最大的可安排空间, 同时将公平性融入到排班计划中, 提高员工的满意程度和人员保留率, 间接降低人员招聘和培训等运营过程成本, 在管理上行之有效.
本文虽对现场调度因素做了一定的考量, 但目前算法仍主要关注班次生成和班次分配阶段, 在今后的研究中可以对现场调度涉及因素更细化地考虑进模型中, 形成一个更科学、更合理的智能排班系统.
| [1] |
van den Bergh J, Beliën J, de Bruecker P, et al. Personnel scheduling: A literature review. European Journal of Operational Research, 2013, 226(3): 367-385. DOI:10.1016/j.ejor.2012.11.029 |
| [2] |
Brucker P, Qu R, Burke E. Personnel scheduling: Models and complexity. European Journal of Operational Research, 2011, 210(3): 467-473. DOI:10.1016/j.ejor.2010.11.017 |
| [3] |
Ernst AT, Jiang H, Krishnamoorthy M, et al. Staff scheduling and rostering: A review of applications, methods and models. European Journal of Operational Research, 2004, 153(1): 3-27. DOI:10.1016/S0377-2217(03)00095-X |
| [4] |
Brunner JO, Stolletz R. Stabilized branch and price with dynamic parameter updating for discontinuous tour scheduling. Computers & Operations Research, 2014, 44: 137-145. |
| [5] |
Stolletz R. Operational workforce planning for check-in counters at airports. Transportation Research Part E: Logistics and Transportation Review, 2010, 46(3): 414-425. DOI:10.1016/j.tre.2009.11.008 |
| [6] |
Lapègue T, Bellenguez-Morineau O, Prot D. A constraint-based approach for the shift design personnel task scheduling problem with equity. Computers & Operations Research, 2013, 40(10): 2450-2465. |
| [7] |
Adams T, O’Sullivan M, Walker C. Physician rostering for workload balance. Operations Research for Health Care, 2019, 20: 1-10. DOI:10.1016/j.orhc.2018.11.001 |
| [8] |
Damcı-Kurt P, Zhang MJ, Marentay B, et al. Improving physician schedules by leveraging equalization: Cases from hospitals in U. S. Omega, 2019, 85: 182-193. DOI:10.1016/j.omega.2018.06.011 |
| [9] |
Bard JF, Purnomo HW. A column generation-based approach to solve the preference scheduling problem for nurses with downgrading. Socio-Economic Planning Sciences, 2005, 39(3): 193-213. DOI:10.1016/j.seps.2004.04.001 |
| [10] |
Gérard M, Clautiaux F, Sadykov R. Column generation based approaches for a tour scheduling problem with a multi-skill heterogeneous workforce. European Journal of Operational Research, 2016, 252(3): 1019-1030. DOI:10.1016/j.ejor.2016.01.036 |
| [11] |
许丹, 刘洪伟, 齐二石. 基于护士排班问题的加班策略比较研究. 系统工程学报, 2018, 33(2): 279-288. |
| [12] |
胡修武, 王瑞程, 王秀利. 呼叫中心坐席人员可加班的优化排班问题. 系统工程, 2019, 37(5): 139-149. |
| [13] |
Maenhout B, Vanhoucke M. A hybrid scatter search heuristic for personalized crew rostering in the airline industry. European Journal of Operational Research, 2010, 206(1): 155-167. DOI:10.1016/j.ejor.2010.01.040 |
| [14] |
Stolletz R, Brunner JO. Fair optimization of fortnightly physician schedules with flexible shifts. European Journal of Operational Research, 2012, 219(3): 622-629. DOI:10.1016/j.ejor.2011.10.038 |
| [15] |
Zeren B, Özkol I. A novel column generation strategy for large scale airline crew pairing problems. Expert Systems with Applications, 2016, 55: 133-144. DOI:10.1016/j.eswa.2016.01.045 |
| [16] |
Smet P, Ernst AT, Berghe GV. Heuristic decomposition approaches for an integrated task scheduling and personnel rostering problem. Computers & Operations Research, 2016, 76: 60-72. |
| [17] |
冯霞, 唐菱, 卢敏. 基于禁忌搜索算法的机场外航服务人员班型生成研究. 电子与信息学报, 2019, 41(11): 2715-2721. DOI:10.11999/JEIT181196 |
| [18] |
冯霞, 唐菱, 卢敏. 面向层次资质的机场外航服务人员排班研究. 交通运输系统工程与信息, 2019, 19(2): 231-237. |
| [19] |
Stolletz R, Zamorano E. A rolling planning horizon heuristic for scheduling agents with different qualifications. Transportation Research Part E: Logistics and Transportation Review, 2014, 68: 39-52. DOI:10.1016/j.tre.2014.05.002 |
 2021, Vol. 30
2021, Vol. 30



