无线传感器网络定位算法根据其定位原理可以分为两类[1]: 基于测距的(range-based)定位算法和非基于测距的(range-free)定位算法. 基于测距的定位算法, 先通过测距技术获得节点之间的距离或角度信息, 再使用三边测量法、三角测量法或最大似然估计法等估算节点位置, 主要算法有TOA[2], TDOA[3], AOA[4]以及RSSI算法[5]. 非基于测距的算法则无需测量节点间距离和角度等信息, 而是利用节点间连通度及邻居关系实现定位, 主要算法有Centroid算法[6]、DV-HOP算法[7]、Amorphous算法[8]以及APIT算法[9].
2 APIT算法基于测距的算法虽然可以取得精度较高的定位结果, 但该类算法对节点硬件要求较高, 并且需要产生大量的计算和通信开销, 不适合大规模应用. 非基于测距的算法在成本、功耗等方面具有明显优势, 对硬件要求也不高, 精度足够满足大部分应用场景, 性价比较高. 相对于其他非基于测距的算法, APIT算法具有较高的定位精度, 以及通信开销小等优点, 具有很强的适用性.
2.1 APIT算法原理APIT算法原理如图1所示, 未知节点从它的通讯范围内所有的锚节点中任意选择3个组成三角形, 通过与其他锚节进行节点信息交换对比来测试该未知节点是否在三角形中, 重复此测试直到穷尽所有可取的三角形组合, 计算包含未知节点的所有三角形的重叠区域, 将重叠区域的质心作为未知节点的估计位置[9].

|
图 1 APIT算法原理图 |
APIT算法在寻找重叠区域时采用网格扫描法[10], 即将定位区域平均分割成正方形网格并给每个网格一个计数器, 若未知节点在三角形内部, 则三角形扫到的网格的计数器加1, 反之则减1, 最终将计数器数值最大的区域的质心作为未知节点的估计位置.
2.2 APIT算法不足及分析一方面, APIT算法虽然与其他非基于测距的算法相比定位精度较高, 但仍有较大提高空间; 另一方面, APIT算法相比其他算法有着相对低覆盖率, 这也是APIT算法另一个研究重点.
APIT算法定位精度的不足, 主要源于在网格扫描法. 在网格扫描法中被三角形扫描到的区域无论大小, 都同样计数器加1, 致使一大一小区域对结果的影响相同. 此外, 未知节点在三角形外时, 存在被误判在三角形内的可能[11], 从而使估计位置产生较大偏差, 定位精度下降.
APIT算法定位覆盖率的不足, 主要源于其算法本身. APIT算法需要未知节点通讯范围内存在3个及以上锚节点才能进行定位, 然而在随机分布的传感器网络中, 锚节点可能在局部密度不足, 致使未知节点通讯范围内锚节点不足3个, 从而无法进行定位, 最终导致定位覆盖率不足[12].
3 APIT与遗传算法混合定位由于上述两点问题的存在, 造成了APIT算法定位精度与定位覆盖率的不足, 为克服此问题, 本文提出了一种APIT算法与遗传算法混合定位算法.
3.1 三角形比较分割针对APIT算法定位精度不足的问题, 本算法在经典APIT算法的网格扫描法部分, 引入三角形比较分割[13]以提高精度. 在△ABC内, 并且边BC>AC>AB, 过A点作BC垂线于D, 即可知∠CDP的大小,若∠CDP小于90°, 则未知节点在△ACD内, 反之, 则在△ABD内, 如图2所示.

|
图 2 三角形比较分割原理图 |
多次应用此判断, 并将所在三角形最长与网格边长比较, 直至最长边长度小于网格边长, 比较分割结束, 具体过程如下:
(1) 通过点A、B、C坐标计算出点D坐标;
(2) 通过RSSI计算出AP、BP、CP长度;
(3) 利用余弦定理与距离公式可计算:
| $\left\{ \begin{array}{l} {\text{∠}} DCP = {\rm{arcos}}\left( {\dfrac{{B{C^2} + C{P^2} - B{P^2}}}{{2BC \cdot CP}}} \right) \\ DP = \sqrt {C{D^2} + C{P^2} - 2CD \cdot CP \cdot \cos {\text{∠}} DCP} \\ {\text{∠}} CDP = {\rm{arcos}}\left( {\dfrac{{C{D^2} + D{P^2} - C{P^2}}}{{2CD \cdot DP}}} \right) \\ \end{array} \right.$ | (1) |
(4) 若∠CDP小于90°, 则未知节点在△ACD内, 反之, 则在△ABD内.
(5) 将未知节点所在三角形边长进行排序, 令最长边为BC, 最短边为AB, 第三边为AC. 若BC大于网格边长, 重复步骤(1)–(4), 反之, 则结束分割.
3.2 遗传算法定位遗传算法[14]是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法. 作为一种优化算法, 遗传算法不依赖于梯度信息, 而是通过模拟自然进化过程来搜索最优解, 具有很好的全局搜优特性. 遗传算法不仅可拓展性高, 便于与其他算法组合优化, 在数学上也易于实现, 其目标函数的定义域可以为任意集合且不会受到连续可微的约束, 这种特点使得遗传算法非常适合求解定位问题 [15].
针对APIT算法定位覆盖率不足的问题, 本算法引入遗传算法对未知节点进行定位[12], 即当未知节点通讯范围内锚节点个数为2时, 在以两个锚节点为圆心, 以通讯范围为半径作圆, 在两圆相交处用遗传算法求解未知节点, 确定目标函数, 使未知节点到锚节点的真实距离与测量距离的绝对误差最小, 将未知节点的求解转换为求解有约束条件的二元二次方程.
| $\left\{ {\begin{array}{*{20}{l}} {f = \displaystyle\sum\limits_{j = 1}^2 {\left| {\sqrt {{{\left( {x - {x_j}} \right)}^2} + {{\left( {y - {y_j}} \right)}^2}} - {d_{i,j}}} \right|} } \\ \sqrt {{{\left( {x - {x_j}} \right)}^2} + {{\left( {y - {y_j}} \right)}^2}} \le R \\ \left| {\sqrt {{{\left( {x - {x_j}} \right)}^2} + {{\left( {y - {y_j}} \right)}^2}} - {d_{i,j}}} \right| \le \delta \\ \end{array}} \right.$ | (2) |
其中,

|
图 3 遗传算法定位原理图 |
遗传算法定位具体过程如下:
(1) 在两圆相交的阴影区域内随机采集N个样本作为初始种群,N个样本的平均坐标作为初始位置, 根据适应度函数
| $\left\{ {\begin{array}{*{20}{l}} \begin{gathered} {f_{i,j}} = 1/1{\rm{ + }}\left| {\sqrt {{{\left( {x\left( {{A_i}} \right) - {x_j}} \right)}^2} + {{\left( {y\left( {{A_i}} \right) - {y_j}} \right)}^2}} - {d_{i,j}}} \right| \\ \end{gathered} \\ {{F_i} = \displaystyle\sum {{f_{i,j}}} } \end{array}} \right.$ | (3) |
(2) 将初始种群中任意一个个体替换为最优个体, 再两两随机配对, 按照一定概率进行交叉操作产生新的个体. 其中, 随机数
| $\left\{ {\begin{array}{*{20}{c}} {{{A'}_i} = {A_i}\alpha + {A_j} \cdot \left( {1 - \alpha } \right)} \\ {{{A'}_j} = {A_j}\alpha + {A_i} \cdot \left( {1 - \alpha } \right)} \end{array}} \right.$ | (4) |
(3) 将种群中的个体, 在可行性区域内向随机方向, 按照一定概率进行变异操作. 其中,
| $\left\{ {\begin{array}{*{20}{c}} {{{A'}_i} = {A_i} + \left| {{R_{\max }} - {A_i}} \right| \cdot \cos \left( \theta \right),\;\cos \left( \theta \right) \ge 0} \\ {{{A'}_j} = {A_j} + \left| {{A_j} - {R_{\min }}} \right| \cdot \sin \left( \theta \right),\;\cos \left( \theta \right) < 0} \end{array}} \right.$ | (5) |
(4) 若达到预设最大迭代次数, 则输出最优解并结束, 否则转到步骤(2).
本文最大迭代次数设置为40.
4 仿真及分析 4.1 实验环境及参数设置本次实验使用Matlab 2016b对算法进行仿真. 在1000 m×1000 m的正方形区域内, 随机分布300个节点, 其中60个为锚节点, 240个为盲节点, 节点通讯距离为200 m, 由此组成一个无线传感器网络进行定位仿真. 遗传算法部分, 初始种群为400个, 交叉概率为0.9, 变异概率为0.02.
4.2 实验结果及分析图4为本文算法在上述仿真环境下, 实验结果与迭代次数的关系.

|
图 4 实验结果与迭代次数关系图 |
由图4可知, 本文算法在迭代40次后, 实验误差逐渐趋近于0, 达到理想状态, 以此确定遗传算法结束条件为最大迭代次数40次, 并将此条件应用于后续仿真.
图5、图6分别为经典APIT算法与本文算法节点分布图. 其中, 红色*表示锚节点的位置, 蓝色○表示未知节点的实际位置. 分布图将未知节点的实际位置与估计位置用线段相连, 用线段的长短来体现未知节点的定位误差, 没有用线段连接的黑色○为无法定位的节点.
图7、图8分别为经典APIT算法与本文算法仿真的误差结果图. 在实验中, 未知节点实际位置与估计位置的欧氏距离与通讯半径的比值被定义为误差, 无法定位的节点数量与未知节点总数量的比值被定义为盲点率.

|
图 5 APIT算法定位节点分布图 |

|
图 6 本文算法定位节点分布图 |

|
图 7 APIT算法定位误差图 |
| $\left\{\begin{array}{*{20}{l}} error={({x}_{{\text{真}}}-{x}_{{\text{估}}})}^{2}+{({y}_{{\text{真}}}-{y}_{{\text{估}}})}^{2}/comm\_r\\ blind\_rate={N}_{{\text{无法定位}}}/{N}_{{\text{未知节点}}} \end{array}\right.$ | (6) |
将两种算法分别仿真100次, 取平均值作为算法结果, 经典APIT算法的误差为32.41%, 盲点率为7.24%; 本文提出的混合算法误差为10.79%, 盲点率2.37%. 结果表明, 本文提出的混合算法相较于经典APIT算法定位精度提高21.62%, 覆盖率提高4.87%.
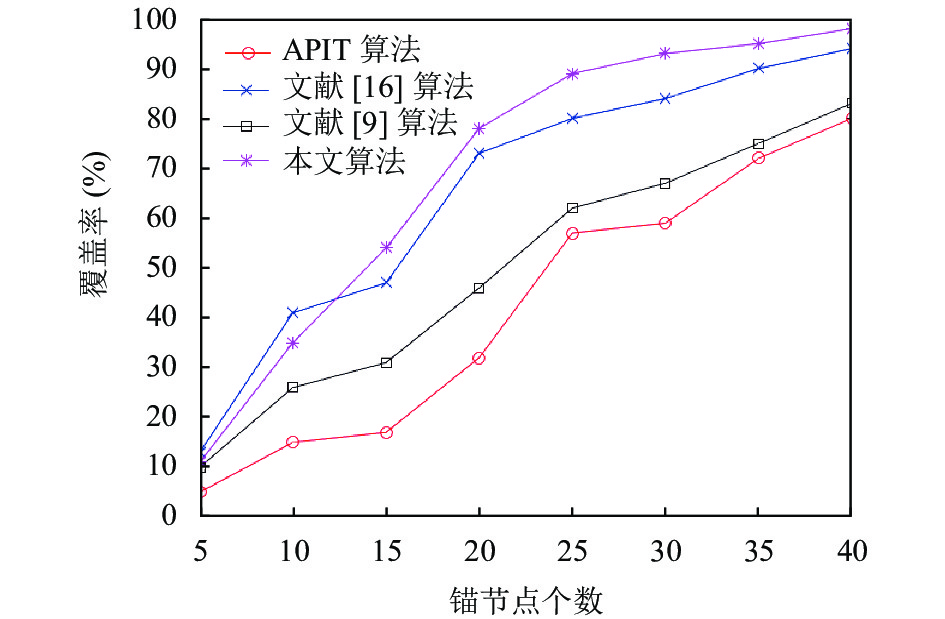
文献[16]提出了一种基于改进差分进化的定位算法, 即DEDV-Hop定位算法, 文献[9]提出了一种基于虚拟节点的定位算法, 即EVN-APIT定位算法. 图9、图10分别为在100 m×100 m区域内, 总节点个数为100个, 锚节点个数从5提升至40时, 几种算法的误差对比图与覆盖率对比图, 对比结果显示, 本算法相较于所比较算法均有不同程度优势.

|
图 8 本文算法定位误差图 |

|
图 9 定位误差对比图 |
5 结论与展望
本文提出一种基于APIT的无线传感器网络混合定位算法. 算法分为两个部分: 当盲节点通讯范围内锚节点数量大于等于3个时, 通过用比较分割法优化过的APIT算法定位; 当盲节点通讯范围内锚节点数量等于2个时, 通过遗传算法进行定位. 仿真实验结果验证了算法的可行性与有效性, 本文算法相较于APIT算法在定位精度与覆盖率上均有不同程度提高.
|
图 10 定位覆盖率对比图 |
| [1] |
孙利民, 李建中, 陈渝, 等. 无线传感器网络. 北京: 清华大学出版社, 2005.
|
| [2] |
Pak JM, Ahn CK, Shi P, et al. Distributed hybrid particle/FIR filtering for mitigating NLOS effects in TOA-based localization using wireless sensor networks. IEEE Transactions on Industrial Electronics, 2017, 64(6): 5182-5191. DOI:10.1109/TIE.2016.2608897 |
| [3] |
Hu DX, Huang Z, Chen X, et al. A moving source localization method using TDOA, FDOA and Doppler rate measurements. IEICE Transactions on Communications, 2016, E99B(3): 758-766. |
| [4] |
Tomic S, Beko M, Dinis R. Distributed RSS-AOA based localization with unknown transmit powers. IEEE Wireless Communications Letters, 2016, 5(4): 392-395. DOI:10.1109/LWC.2016.2567394 |
| [5] |
Wang ZM, Zheng Y. The study of the weighted centroid localization algorithm based on RSSI. Proceedings of 2014 International Conference on Wireless Communication and Sensor Network. Wuhan: IEEE, 2015. 276–279.
|
| [6] |
Bulusu N, Heidemann J, Estrin D. GPS-less low-cost outdoor localization for very small devices. IEEE Personal Communications, 2000, 7(5): 28-34. DOI:10.1109/98.878533 |
| [7] |
Niculescu D, Nath B. DV based positioning in ad hoc networks. Telecommunication Systems, 2003, 22(1–4): 267-280. |
| [8] |
Shen SK, Yang B, Qian K, et al. An improved amorphous localization algorithm for wireless sensor networks. Proceedings of 2016 International Conference on Networking and Network Applications. Hakodate: IEEE, 2016. 69–72.
|
| [9] |
沈利祥. 无线传感器网络中基于APIT定位算法的研究[硕士学位论文]. 南京: 南京邮电大学, 2019.
|
| [10] |
许佳慧, 陈柯宇, 程恩. 水下传感网络的低复杂度APIT算法及OPNET仿真实现. 系统仿真学报, 2020, 32(1): 27-34. |
| [11] |
周勇, 夏士雄, 丁世飞, 等. 基于三角形重心扫描的改进APIT无线传感器网络自定位算法. 计算机研究与发展, 2009, 46(4): 566-574. |
| [12] |
章磊, 段莉莉, 钱紫鹃, 等. 基于遗传算法的WSN节点定位技术. 计算机工程, 2010, 36(10): 85-87. DOI:10.3969/j.issn.1000-3428.2010.10.028 |
| [13] |
张婧, 国晶. 基于迭代分割的无线传感器网络定位算法. 长春理工大学学报(自然科学版), 2019, 42(5): 116-121. |
| [14] |
雷英杰, 张善文. MATLAB遗传算法工具箱及应用. 西安: 西安电子科技大学出版社, 2014.
|
| [15] |
石琴琴, 霍宏, 方涛, 等. 使用最速下降算法提高极大似然估计算法的节点定位精度. 计算机应用研究, 2008, 25(7): 2038-2040. DOI:10.3969/j.issn.1001-3695.2008.07.035 |
| [16] |
黄亚萍. 基于改进差分进化的无线传感器网络节点定位技术研究[硕士学位论文]. 南京: 南京邮电大学, 2020.
|
 2021, Vol. 30
2021, Vol. 30



