2011年德国提出“工业4.0计划”, “工业4.0”是指以智能制造为主导的第4次工业革命, 旨在实现智能工厂、智能生产、智能物流, 从而实现智能制造. 这和中国制造2025的主题思想是一致的, 都是推动制造业向智能化方向转型. 现如今工业生产已经基本实现自动化, 要想实现自动化到智能化的过度, 需要寻找一种新的方案来弥补自动化生产中的不足. 随着大数据时代的来临, 人脸识别技术、车牌识别技术、语音识别、智能停车场等一系列智能产品应用走进人们的生活. 人工智能可以实现在某些方面替代人的作用, 应用于工业生产中将会在解放劳动力同时提高生产效率, 是推动工业生产走向智能化的第一大助力. 标识识别技术作为人工智能的一种, 同样在工业生产中占据了重要的作用, 现如今比较火热的瓶盖封装检测、汽车智能生产都和标识识别技术密切相关. 但是在一些传统的工业生产中, 标识识别技术还难以应用, 如墙材生产线、水泥粉磨生产线等. 其主要原因就是生产环境恶劣, 噪声复杂多变, 标识识别技术难以推广. 本次研究以卷积神经网络CNN[1-7]为核心, 通过对算法的改进和多种算法结合, 寻找一种能够在高噪声环境下对标识精准识别的方法.
与其它标识识别技术研究内容不一样, 高噪声环境下, 首先要考虑的是对标识牌的精准提取问题, 精准提取的前提是能够准确定位到标识牌的边缘, 这就需要用到边缘检测算法[8-10], 目前比较流行的边缘检测算法大部分是在基于检测算子来实现的, 其中效果比较好的边缘检测算子有Sobel算子[11]、Prewitt算子、Roberts算子、Canny算子[12,13]. Canny边缘检测算子在抑制多边缘响应和边缘精细度上具有较好的效果, 但是在高噪声环境下, Canny边缘检测算子还是难以满足对边缘精准提取的需求, 文中对Canny边缘检测算法加以研究改进, 使其能够在高噪声环境下实现对标识边缘得定位, 提取标识得边缘信息, 进而实现对标识牌得精准提取, 构建标识牌数据集, 为卷积神经网络得训练做准备.
1 标识数据采集 1.1 标识牌设定墙材生产中工作环境是比较恶劣的, 灰尘浓度较大, 噪声干扰较多. 标识牌镶嵌在窑车壁的下方, 要随同窑车进入烧坯窑, 烧坯窑上层温度最高可达到1300 ℃, 下层最高温度可达到400 ℃, 考虑其高温特性的影响, 标识牌经过灼烧后颜色会发生改变, 如果单纯的利用颜色的特性来做识别的话很难实现, 另外在标识牌的材质上要选用耐高温的钢材质. 针对标识牌的颜色多变的特性, 利用镂空的圆孔的二进制排列来代替纯数字标识, 圆孔的特征值较为明显, 不易被灰尘遮挡, 镂空的圆孔凹凸感强烈, 光照时产生的色差明显, 在高噪声的工业环境下便于识别. 标识牌上最多可以刻8个圆孔, 圆孔依照二进制进行排列, 能够对28=256辆标识物标记, 其排列结构如图1, 标识牌长10 cm, 宽5 cm, 圆孔直径大小为1.5 cm, 圆孔之间的间隔为1 cm.

|
图 1 标识牌结构图 |
1.2 数据采集
首先需要采集大量的标识数据做数据集, 通过对数据集训练来构造训练模型. 数据采集的核心部分是对标识牌提取, 这就需要用到边缘检测算法Canny, 边缘检测算法可以通过提取标识牌的边缘信息, 来确定标识牌的大小和具体所在位置, 为标识牌的精准提取做准备. 传统的Canny边缘检测算法在对边缘提取时容易造成边缘缺失, 导致提取精度不够, 无法对标识牌精准提取. 这主要是由于Canny边缘检测算法中高斯降噪[8]部分导致的, 高斯降噪在去除高斯噪声的同时会降低图片的边缘信息, 导致边缘信息缺失. 因此需要对Canny中的高斯降噪部分进行改进, 在保留降噪功能的同时能保留边缘信息.
高斯降噪主要通过构建高斯卷积核与图像进行卷积运算, 利用权重因素对高斯噪声加以模糊处理, 使图像变得平滑. 分别取含有边缘和未含有边缘信息的像素矩阵, 如图2所示.

|
图 2 像素矩阵 |
从图2中可以看出含有边缘得像素矩阵第1列和第2列以及第3列像素值差异较大, 未含有边缘信息得像素值差异较少. 高斯降噪中, 中心点像素值由其余8个像素点加权平均得到, 未含有边缘信息的像素矩阵与权重进行卷积运算后, 中心像素值变化不大, 含有边缘信息的像素矩阵则与其相反, 这样会将差异较大的边缘像素值模糊掉.
从图3中可以看出包含边缘信息的中心像素值变化较大, 由145变为126, 未包含边缘信息的像素值基本不变, 该过程是造成边缘信息缺失的主要因素, 因此需要对高斯模糊算法进一步优化, 降低其降噪过程中对边缘的模糊程度.

|
图 3 卷积运算后像素值变化 |
这里选用双边滤波[14]来代替高斯模糊算法, 双边滤波能够在平滑图像去噪的同时可以很好地保留边缘信息, 这主要是由于它的滤波器核由空间域核和值域核生成, 空间域核是由每个像素的位置对应的欧式距离决定的模板权值, 公式如下:
| $ {w_d}\left( {i,j,k,l} \right) = {\rm{exp}}\left( { - \frac{{{{\left( {i - k} \right)}^2} + {{\left( {j - l} \right)}^2}}}{{2\delta _d^2}}} \right) $ | (1) |
其中,i,j代表的是坐标矩阵y(i,j)中的坐标点, 定义为q(i,j),k,l为坐标矩阵y(i,j)中的中心坐标点, 定义为p(i,j), 对应高斯函数的标准差, 属于上面讲解的高斯核函数, 从式(2)中可知, 是计算临近点q到中心点p的临近程度, 因此空间域核是用来衡量空间临近的程度.
值域核表示图像中像素的差值决定的模板权值, 公式如下:
| $ {{{w}}_{{r}}}\left( {{{i}},{{j}},{{k}},{{l}}} \right) = {\rm{exp}}\left( { - \frac{{\left| {} \right|{{f}}\left( {{{i}},{{j}}} \right) - {{f}}({{k}},{{l}}){{\left| {} \right|}^2}}}{{2\delta _{{r}}^2}}} \right) $ | (2) |
其中, f(i,j)对应坐标点y(i,j)的像素值, f(k,l)为y(i,j)中心坐标点对应的像素值, 为高斯函数的标准差, 值域核的范围在[0, 1]之间.
将式(1)和式(2)相乘就可以得到双边滤波器的模板权值, 如式(3)所示.
| $ \begin{split} & w\left( {i,j,k,l} \right) = {w_d}\left( {i,j,k,l} \right)×{w_r}\left( {i,j,k,l} \right)\\ & = {\rm{exp}}\left( { - \frac{{{{\left( {i - k} \right)}^2} + {{\left( {j - l} \right)}^2}}}{{2\delta _d^2}} - \frac{{\left| {} \right|f\left( {i,j} \right) - f(k,l){{\left| {} \right|}^2}}}{{2\delta _r^2}}} \right) \end{split} $ | (3) |
进一步化简可以得到双边滤波器的数据, 如式(4)所示.
| $ g\left(i,j\right)=\frac{{\displaystyle\sum }_{kl}f\left(k,l\right)w(i,j,k,l)}{{\displaystyle\sum }_{kl}w(i,j,k,l)} $ | (4) |
从式(4)可知, 双边滤波是结合了高斯滤波和-截尾均值滤波器的一些特点, 综合了值域和空间域上的差别, 高斯滤波器只是利用了像素间的欧式距离来分配权重, 其使用的模板系数随着距离中心像素的距离增加而减少; 截尾均值滤波器利用局域内像素灰度值间的差, 去除最大值和最小值后再进行均值化, 实现对图像降噪的功能.
式(1)中, 空间域求的是n × n(n为空间域核的大小)局域内的坐标点(p)到中心坐标点(q)的距离, 距离的远近用来衡量像素之间的关联度, 而值域计算的是m × m(m为值域核的大小)局域内周边像素值和中心像素值的近似程度, 在图像上直观的理解就是, 当图像处于没有边缘信息的平坦区域, 局域内像素值差值较小, 值域趋近于1, 这时候就相当于对该部分进行高斯滤波, 在非边界区域相当于进行高斯滤波, 反之, 局域内像素值差值较大, 对应的值域趋近于0, 导致趋近于0, 当前像素收到的影响变小, 保留图像的边缘细节信息, 达到对图像降噪的同时, 保留图像边缘信息的效果.
原始图像中由于摄像头采集图片时光照的影响, 采集的图片会含有高斯噪声点, 需要用高斯滤波去除掉, 图4为降噪之前和高斯降噪之后的对比, 降噪之后高斯噪声点消失, 图像边缘变得模糊. 图5进行边双边滤波降噪之后, 噪声消失, 图像边缘清晰, 有利于边缘算子对图像边缘的提取.

|
图 4 高斯降噪 |

|
图 5 双边滤波降噪 |
Canny边缘检测算法主要由4部分组成: ① 对图像进行高斯降噪; ② 选用Sobel算子计算梯度幅值和方向; ③ 根据幅值对图像进行非极大值抑制; ④ 用双阈值算法检测和链接边缘. 本文中将 ① 中的高斯降噪算法由双边滤波算法代替, 在降噪的基础上增强边缘信息, 图6分别展示了高斯降噪和双边的边缘提取效果, 图7展示了标识牌的提取效果, 能够对标识牌实现精准提取.

|
图 6 边缘提取 |

|
图 7 标识牌提取 |
从提取效果来看, 改进之后可以对标识牌精准提取, 符合提取要求.
2 模型训练本文利用椭圆拟合算法和卷积神经网络相结合. 标识牌是由圆孔的二进制排列实现的, 以第285个标识牌为例, 只有当识别结果与标签285对应, 且椭圆拟合得出的圆孔个数和实际标识牌圆孔个数相一致时, 才判定识别结果正确, 这样会一定程度上降低识别错误率.
2.1 CNN卷积神经网络通过改进的Canny算法对标识牌进行采集, 共提取到8000组数据用于训练, 模型选用在图像识别方向应用较好的卷积神经网络, 其结构特征图如图8所示.
隐含层包含卷积层, 池化层和全连接层.
| $ \left\{ {\begin{array}{l} {y}(i,j)=[G*w]+b\\ ={\displaystyle \sum _{e=1}^{{E}}{\displaystyle \sum _{x=1}^{f}{\displaystyle \sum _{y=1}^{f}{\displaystyle \sum _{a=1}^{A}[{G}_{e}(si+x,sj+y){w}_{a}}}}}(x,y)]+b\\ ({i},j)\in \{0,1,2,\cdots ,{L}_{l+1}\},\; {L}_{l+1}=\left|\dfrac{{L}_{l}}{s}\right|\end{array} } \right.$ | (5) |

|
图 8 CNN网络结构图 |
假设输入为G, 隐含层只含有卷积层, 则输出可以用式(6)来表示. G和y(i,j)为卷积层输入和输出, w为权重, b为偏置, e为卷积输出对应的通道数, Ll为输入尺寸, f、s和p分别对应卷积核大小、卷积步长和填充, 这样可以通过参数Ll、s得到下一卷积层的输入尺寸Ll+1. 卷积层个数为2, 卷积核大小为3×3, 通道数e为3, 步长为1, 假设输入G=(G1,…, Gn,…, GN), 个数为N个, 隐含层输出y=(y1,…,yn,…,yq), 隐含层神经元个数为q个, 输出层Z=(Z1,…
| $\left\{ {\begin{array}{l} {{{y}}_{\rm{1}}} = [{G_1}*{w_1}] + b_1^{(1)} = \displaystyle\sum\limits_{{{i}} = 1}^{{N}} {\displaystyle\sum\limits_{l = 1}^N {[{G_i}*{w_{l1}}} } ] + b_1^{(1)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdots \\ {{{y}}_{{n}}} = [{G_n}*{w_n}] + b_1^{(2)} = \displaystyle\sum\limits_{{{i}} = 1}^{{N}} {\displaystyle\sum\limits_{l = 1}^N {[{G_i}*{w_{lm}}} } ] + b_1^{(2)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdots \\ {{{y}}_{{q}}} = [{G_q}*{w_q}] + b_1^{(3)} = \displaystyle\sum\limits_{{{i}} = 1}^{{N}} {\displaystyle\sum\limits_{l = 1}^N {[{G_i}*{w_{lM}}} } ] + b_1^{(3)} \end{array} } \right.$ | (6) |
在卷积层中每个神经元连接数据窗的权重是固定的, 每个神经元只关注一个特性. 神经元就是图像处理中的滤波器, 比如边缘检测专用的Sobel滤波器, 即卷积层的每个滤波器都会有自己所关注一个图像特征, 比如垂直边缘, 水平边缘, 颜色, 纹理等等, 这些所有神经元加起来就好比就是整张图像的特征提取器集合, 通常这些特征是以非线性的关系进行组合, 为了增加表达的复杂性, 把线性关系转化为非线性关系, 卷积层添加激励函数 ReLU (Rectified Linear Unit), 把卷积层输出结果做非线性映射, 一定程度上避免了梯度消失和梯度饱和的问题. 其表达形式如式(7).
| $ {{A}}_{{{i}},{{j}},{{k}}}^{\rm{l}} = f\left( {Z_{i,j,k}^l} \right) $ | (7) |
其中, Z为输入, A为输出, f为激励函数, 则输出可以由式(8)得到.
| $\left\{ {\begin{array}{l} {{{\textit{z}}}_{\rm{1}}} = [f({y_1})*{v_1}] + b_2^{(1)} = \displaystyle\sum\limits_{{{i}} = 1}^{{q}} {\displaystyle\sum\limits_{l = 1}^q {[f({y_i})*{v_{l1}}} } ] + b_2^{(1)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdots \\ {{{\textit{z}}}_{{n}}} = [f({y_n})*{v_n}] + b_2^{(2)} = \displaystyle\sum\limits_{{{i}} = 1}^{{q}} {\displaystyle\sum\limits_{l = 1}^q {[f({y_{{i}}})*{v_{lm}}} } ] + b_2^{(2)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdots \\ {{{\textit{z}}}_{{N}}} = [f({y_N})*{v_N}] + b_2^{(3)} = \displaystyle\sum\limits_{{{i}} = 1}^{{q}} {\displaystyle\sum\limits_{l = 1}^q {[f({y_i})*{v_{l1}}} } ] + b_2^{(3)} \end{array}} \right. $ | (8) |
另外在卷积层后, 一般需要加入池化层主和全连接层, 池化层可以在保留主要特征的前提下, 减少参数的运算量. 常见的池化方式有两种, 均值池化和极大值池化. 本文采用均值池化的方法, 池化公式如下所示.
| ${{A}}_{{k}}^{{l}}(i,j) = {\left[ {\sum\limits_{x = 1}^f {\sum\limits_{y = 1}^f {A_k^l{{(si + x,sj + y)}^p}} } } \right]^{\frac{1}{p}}} $ | (9) |
其中, p为预指定参数, 均值池化时p=1, 其余参数和卷积层的相同, 均值池化会模糊掉边缘的特征值, 为了保留边缘特征值, 这里采用极大值池化的方式. 全连接层主要把训练参数铺展开来, 对提取的特征进行非线性组合, 在这里加入dropout, 以一定的概率舍弃神经元, 可以避免训练中存在的一定的偶然性, 使训练得到更好的效果. 模型训练的整体结构图如图9所示.

|
图 9 CNN模型结构图 |
该模型训练结构由5部分组成, 分别包括1个输入层、3个卷积层、3个池化层、2个全连接层、1个输出层组成, 忽略梯度爆炸和梯度消失等问题, 层数越多, 网络感受野越广, 提取的特征值信息越多, 有利于提高识别准确率, 但是层数的加深会造成运算数量的增多, 在实时性要求比较高的墙材生产线中难以满足要求, 实际的测试过程中, 既要考虑图像识别的准确性, 又要考虑识别时的实时性, 该研究是在基于树莓派平台上实现的, 运行效率较低, 过多的运算量会造成运行堵塞, 太深的模型难以运行.
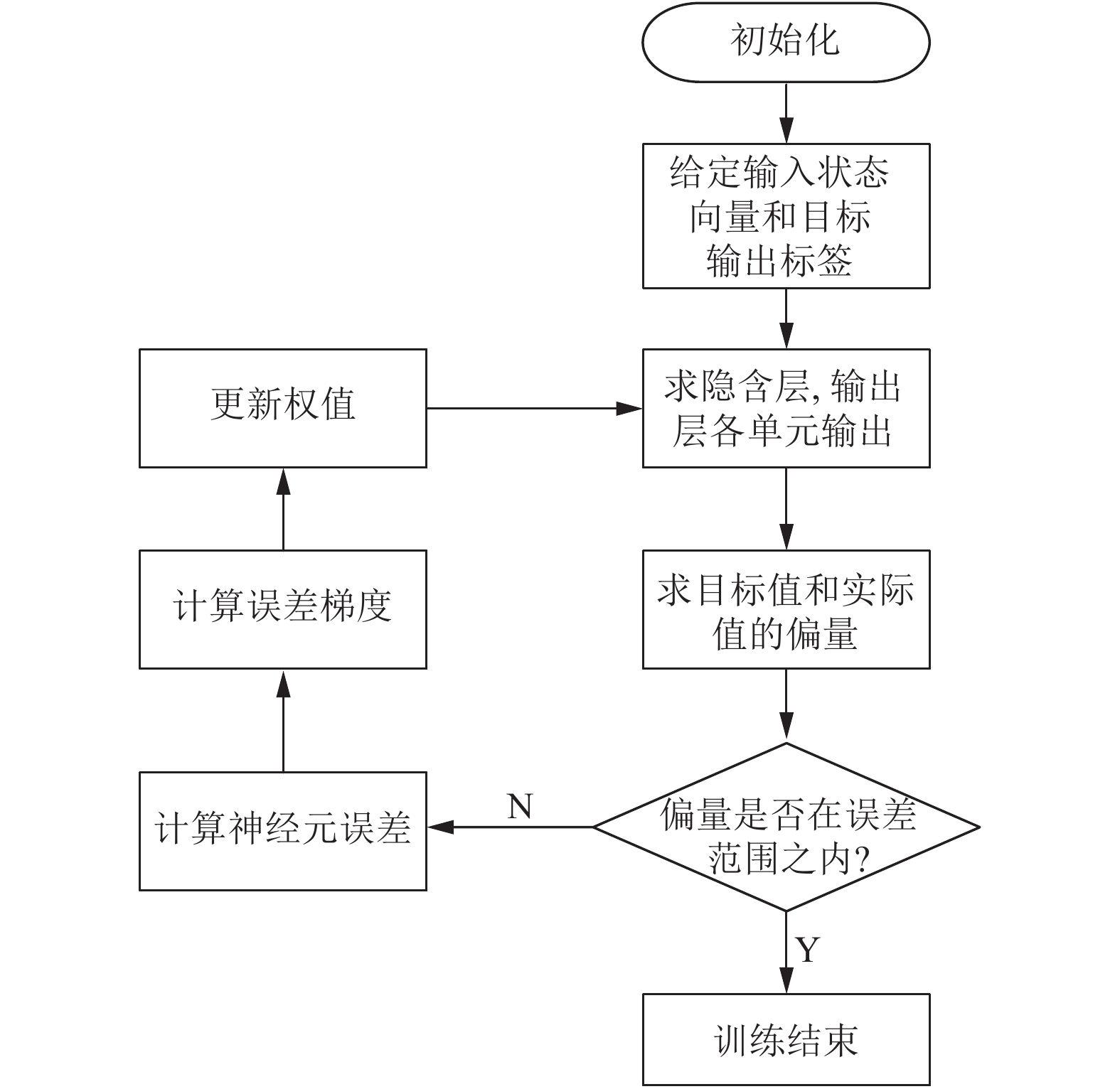
根据整体训练过程可以分为5部分: ① 权重初始化; ② 确定输入向量和输出值; ③ 根据权重和输入向量值求出隐含层和输出层各单元的输出; ④ 计算输出和实际值之间的偏量; ⑤根据偏量值判断训练结果是否满足要求, 满足要求则输出训练模型, 训练结束, 不满足则重复执行②以后的步骤, 直到满足要求, 输出训练模型. 详细流程步骤, 如图10所示.
2.2 椭圆拟合已知椭圆方程可以由式(10)表示.
| $\left\{\begin{array}{l} {{a}}{{{x}}^{\rm{2}}} + bxy + c{y^2} + dx + ey + f = 1 \\ 4ac - {b^2} = 1 \end{array} \right.$ | (10) |
其中, a, b, c, d, e,f为常数项, 令A=[a,b, c,d,e,f]T, X=
| $\left\{ {\begin{array}{l} {{{\rm{min}}||DA|}}{{\rm{|}}^{\rm{2}}} \\ {{{A}}^{\rm{T}}}CA = 1 \end{array} } \right.$ | (11) |
其中, D为数据样本集合n× 6, 6表示维度, 对应6个常数系数, n表示样本数, C为矩阵常数矩阵. 根据拉格朗日乘子法, 引入拉格朗日因数β, 得到以下两个等式.
| $\left\{ {\begin{array}{l} {\rm{2}}{{{D}}^{\rm{T}}}DA - 2\beta CA = 0 \\ {A^{\rm{T}}}CA = 1 \end{array} } \right.$ | (12) |
令S=DTD, 那么上述方程可以改写为:
| $\left\{ {\begin{array}{l} {{S}}A = \beta CA \\ {A^{\rm{T}}}CA = 1 \end{array}} \right. $ | (13) |
求解式(10)的特征值和特征向量(βi,θi), 那么同样地(βi,gθi)也是式(14)的特征解, 其中, g是任意的实数, 根据方程ATCA=1, 可以很容易地找到一个g, 使得g2θiTCθi=1, 即:
| $ {{{g}}}_{{i}}=\sqrt{\frac{1}{{\theta }_{i}^{{\rm{T}}}C{\theta }_{i}}}=\sqrt{\frac{{\beta }_{i}}{{\theta }_{i}^{{\rm{T}}}S{\theta }_{i}}}$ | (14) |
最后令ɑi=giθi, 取g>0时对应的特征向量θ, 即可作为椭圆拟合曲线的特征解, 另外可以通过设定椭圆长短轴的比例值, 对想要的椭圆进行拟合, 排除干扰性椭圆. 椭圆拟合示例图如图11.
|
图 10 CNN训练流程 |

|
图 11 标识牌椭圆拟合效果图 |
2.3 椭圆拟合和CNN相结合
该识别系统是在基于轻量级嵌入式设备树莓派上运行的, 运行内存有限, 加深训练模型会导致运行内存不够用, 难以形成可靠的识别系统. 为了满足实时性和可靠性的要求, 进一步结合模型, 采用椭圆拟合和卷积神经网络相结合的原理来提高准确率, 整体模型训练结构图如图12所示. 通过圆孔个数和CNN识别结果的对比, 来判断识别结果, 增强模型的分类能力.

|
图 12 整体模型构建流程图 |
3 训练结果
首先选用1万组数据集对CNN模型进行测试, 测试结果如图13所示, 从图13中可以看出准确率上升波动较大, 损失函数直线下降后趋于稳定, 不符合一般的训练规律, 考虑产生了过拟合, 调整学习率并增大数据集到4万组, 另外增大dropout率, 舍弃掉无用的特征信息, 再次利用数据集进行训练, 训练结果如图14所示.
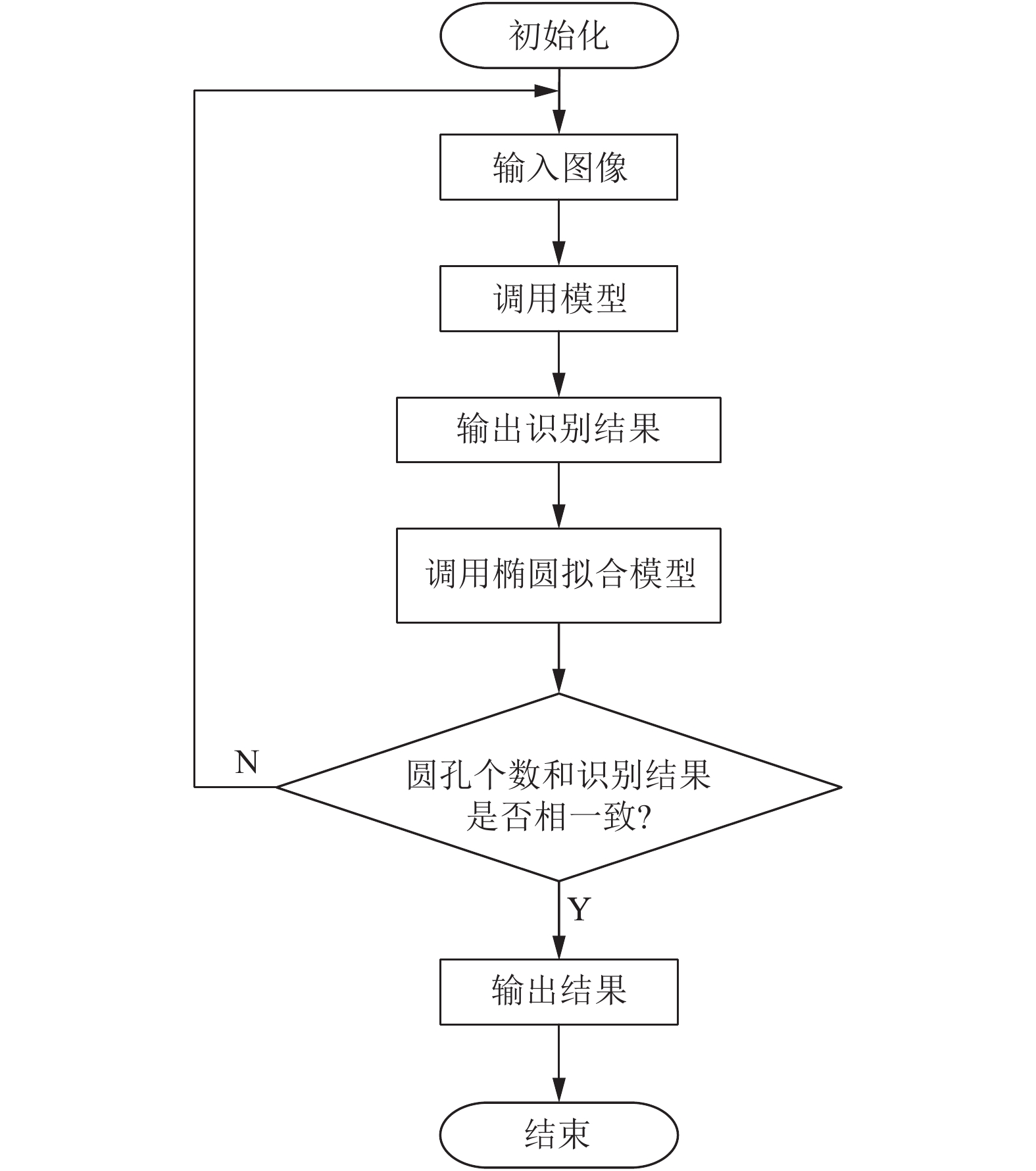
改变数据集和dropout率之后, 正确率上升趋于稳定, 损失函数下降符合一般规律, 这表明模型训练过程满足要求, 但是识别正确率较低, 趋于0.8左右, 增大识别准确率虽然可以通过加深训练模型的方法来提高, 但是加深训练模型的同时必然会加大训练参数的运算量, 难以实现再轻量级嵌入式设备上运行, 因此采用椭圆拟合和CNN相结合的思路来提高识别率, 训练结果如图15所示, 识别流程图如图16所示. 准确率与单独的CNN相比有显著的提高, 稳定在0.96左右, 满足模型训练要求.

|
图 13 单独CNN训练结果 (1万组数据集) |

|
图 14 单独CNN训练结果 (4万组数据集) |

|
图 15 椭圆拟合和CNN相结合训练结果 |
|
图 16 识别流程图 |
4 总结
本文采用椭圆拟合和CNN相结合的思路, 提高了对标识牌的识别准确率, CNN和椭圆拟合算法相结合, 标识识别率从0.8提高至0.96左右, 能够实现对标识牌的精准识别. 在标识牌提取上, 对Canny边缘检测算法中的高斯模糊算法进一步改进, 使其在对图像降噪的同时能够保留边缘信息, 便于对标识牌的精准提取. 虽然本文实现了对标识牌的精准识别, 但是在实时性上还待进一步改进, 改进的高斯模糊算法在运行速度上要低于传统的高斯模糊算法, 并且椭圆拟合算法只适合带有圆孔的标识牌, 在通用性上较弱, 还待进一步完善.
| [1] |
Hussain BA, Hathal MS. Developing Arabic License Plate Recognition System Using Artificial Neural Network and Canny Edge Detection. Baghdad Science Journal, 2020, 17(3). |
| [2] |
江帆, 刘辉, 王彬, 等. 基于CNN-GRNN模型的图像识别. 计算机工程, 2017, 43(4): 257-262. DOI:10.3969/j.issn.1000-3428.2017.04.044 |
| [3] |
成秘. 改进CNN的图像分类模型研究[硕士学位论文]. 阜新: 辽宁工程技术大学, 2020.
|
| [4] |
Su Y. A parallel computing and mathematical method optimization of CNN network convolution. Microprocessors and Microsystems, 2021, 80: 103571. DOI:10.1016/j.micpro.2020.103571 |
| [5] |
薛昆南. 基于卷积神经网络的视觉识别研究[硕士学位论文]. 广州: 华南农业大学, 2016.
|
| [6] |
林旭斌. 基于CNN的视觉交互中图像处理关键技术研究[硕士学位论文]. 广州: 华南理工大学, 2017.
|
| [7] |
何锐波, 狄岚, 梁久祯. 一种改进的深度学习的道路交通标识识别算法. 智能系统学报, 2020, 15(6): 1121-1130. |
| [8] |
朱地博, 李春贵, 张延丽. 抗噪形态学图像边缘检测算法的研究. 信息技术, 2017(7): 115-117. |
| [9] |
李向前. 基于边缘检测的非局部均值图像去噪算法. 电脑编程技巧与维护, 2020(8): 3-6, 10. DOI:10.3969/j.issn.1006-4052.2020.08.002 |
| [10] |
许蓉, 王直, 宗涛. 基于改进高斯滤波的医学图像边缘增强. 信息技术, 2020, 44(4): 75-78. |
| [11] |
朱加乐. 基于Sobel算子及改进的最小二乘圆拟合的PET瓶口缺陷检测[硕士学位论文]. 南京: 南京大学, 2017.
|
| [12] |
夏建芳, 巢军. 一种改进的Canny边缘检测算法. 电子世界, 2017(10): 22-23. DOI:10.3969/j.issn.1003-0522.2017.10.012 |
| [13] |
李长有, 陈国玺, 丁云晋. 改进Canny算子的边缘检测算法. 小型微型计算机系统, 2020, 41(8): 1758-1762. DOI:10.3969/j.issn.1000-1220.2020.08.031 |
| [14] |
Jin LH, Xiong CQ, Liu H. Improved bilateral filter for suppressing mixed noise in color images. Digital Signal Processing, 2012, 22(6): 903-912. DOI:10.1016/j.dsp.2012.06.012 |
| [15] |
梁琼, 赵慧民, 葛任贤, 等. 基于椭圆拟合的改进Hough变换算法在眼控系统中的应用研究. 广东技术师范大学学报, 2020, 41(3): 9-15. DOI:10.3969/j.issn.1672-402X.2020.03.003 |
| [16] |
郑增, 李明, 韦庆玥, 等. 基于OpenCV的椭圆特征识别算法改进. 计量与测试技术, 2019, 46(8): 86-88, 93. |
 2021, Vol. 30
2021, Vol. 30



