近年来, 我国经济的高速增长促使着人们追求更高的生活品质, 人们的航空出行需求迅速增长, 给机场带来了不小的压力. 机场的旅客吞吐量是民用机场的主要生产指标, 旅客流量是机场对资源进行高效配置的依据, 是机场进行决策的基本前提. 因此, 客流量的预测对机场的管理和建设有很大的参考意义.

传统的机场客流量预测多为基于线性假设的模型. 如陈玉宝等^[1]以首都机场为例采用组合预测方法对旅客吞吐量进行预测. 俞佳立等^[2]运用指数平滑法与灰色预测法两者的组合预测模型对管道货运量进行预测分析. 刘夏等^[3]基于三亚机场2008–2016年的月度客流量数据, 运用ARMA模型、灰色预测模型、ARMA改进回归模型对客流预测及数据仿真. 由于线性模型对机场流量预测的局限性(交通流量因自由流、阻塞、故障和恢复情况等频繁变化而具有非线性特征), 上述模型的性能和应用都受到限制. 近年来学者们开发出各种机器学习与深度学习的模型应用于交通流预测. 钟颖等^[4]把极端样度上升(XGBoost)模型用于路段短时交通流的预测. 周燎等^[5]用期望最大化(EM)算法从交通流数据中学习出贝叶斯动态线性模型(DLM)的关键参数, 对下一时刻的车流量进行预测. 朱征宇等^[6]建立了支持向量机与卡尔曼滤波组合模型,并将该模型应用于短时交通流量预测. 衡红军等^[7]用动态回归ARIMAX模型, 对航站楼内短时段的值机旅客人数进行预测. Ma等^[8]将递归神经用于交通速度预测的网络(RNN). Polson和Sokolov^[9]提出了一种深度学习架构来捕捉非线性时空效应. Huang等^[10]提出了一个由深度信任网络(DBN)和一个多任务回归层组成的预测短期交通流的体系结构.

本文提出的是一种基于注意机制的编码-解码结构时序预测模型(Temporal Attention-based Encoder-Decoder model, TAED), 把基于注意机制的融合双向长短时记忆网络编码-解码模型应用到机场客流量预测. 由于深度神经网络在长时间尺度的预测中存在着淹没前期输入信号的缺点, 因此, 在设计深度学习预测方法时引入注意力机制, 使模型能够根据不同时期输入信号对于输出结果的贡献强度分配不同的关注度, 从而使模型具备处理大时间尺度序列的能力. 同时对于标准的编码解码模型对时间序列数据的特征提取能力弱的问题, 引入了Bi-LSTM, 使模型能够对数据特征进行充分学习, 捕捉不同时间段的隐含特征. 此外, 时间序列数据的多步前向预测比单步预测困难, 而序列-序列学习结构可以很好地解决这一问题. 由于上述优势, TAED模型相对于经典LSTM模型能够更好的捕捉时间序列中的隐含特征, 并且对于前期输入信号有更好的记忆力, 因而具有更好的预测效果.

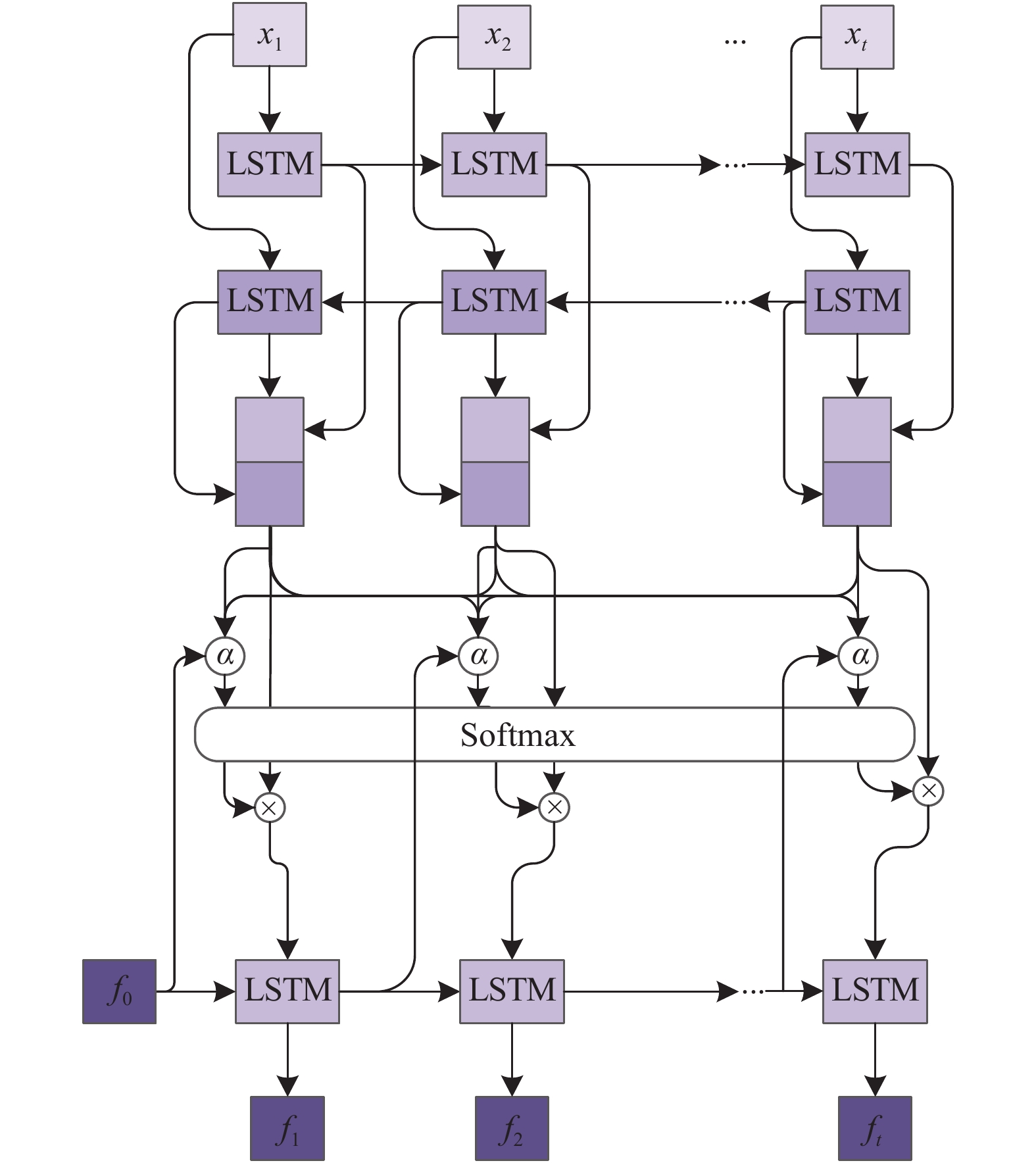
1 基于时间注意机制的编码解码模型 1.1 本文框架

本文提出的基于注意机制的多变量时间序列多步预测框架(如图1). 该框架由Bi-LSTM、LSTM和基于时间注意机制的上下文层3部分组成. Bi-LSTM用于学习任意长度的输入数据的隐藏表示, 从时间序列中提取出深层的时间依赖特征, 然后利用时间注意层构造潜在的空间变量(时间注意上下文向量). LSTM解码器根据生成的潜在空间变量, 对未来的时间序列值进行预测. 图1给出了该框架的图解, 该框架可以端到端对时间序列数据建模.

1.2 编码解码结构

LSTM是一种处理具有时间序列特征数据的长期学习模型^[11]. 典型的LSTM包括5个部分: $ {i}_{t}、{f}_{t}、$ $ {s}_{t}、{o}_{t}、{h}_{t}$ , 分别作为输入门、遗忘门、存储单元、输出门以及LSTM单元的隐藏状态. 一个典型的LSTM单元块包括3个门和1个存储单元, 基于这些部分使得其具有忘记或记忆信息的能力(决定信息是否传输到下一个单元格).

${i_t} = \sigma ({U^{(i)}}{x_t} + {W^{\left( i \right)}}{h_{t - 1}} + {b_i})$

(1)

${f_t} = \sigma ({U^{(f)}}{x_t} + {W^{\left( f \right)}}{h_{t - 1}} + {b_f})$

(2)

${o_t} = \sigma ({U^{(o)}}{x_t} + {W^{\left( o \right)}}{h_{t - 1}} + {b_o})$

(3)

${\tilde s_t} = \tanh ({U^{(c)}}{x_t} + {W^{\left( c \right)}}{h_{t - 1}} + {b_c})$

(4)

${s_t} = {f_t} \odot {s_{t - 1}} + {i_t} \odot {\tilde s_t}$

(5)

${h_t} = {o_t} \odot \tanh ({s_t})$

(6)

式中, 对于输入的时间序列值在 $t$ 时间步时, LSTM单元计算一个隐藏状态 $h{}_t$ 和一个内存状态 $S{}_t$ , $\sigma $ 是激活函数, $ \odot $ 是元素的乘法, 这是输入时间序列值的编码.

但传统的LSTM有一个缺点, 它只能学习时间序列数据的前一个上下文, 不能学习同一序列数据的前向上下文. 所以我们用Bi-LSTM作为编码器, 可以同时处理两个不同方向的数据互连的隐藏层: 单向进程使用从 $t = 1$ 到T的前向隐藏层; 另一个方向进程使用从 $t = T$ 到1的后向隐藏层. 这个经典的Bi-LSTM计算过程如下:

${\vec i_t} = \sigma ({\vec U^{(i)}}{\vec x_t} + {\vec W^{\left( i \right)}}{\vec h_{t - 1}} + {\vec b_i})$

(7)

${\vec f_t} = \sigma ({\vec U^{(f)}}{\vec x_t} + {\vec W^{\left( f \right)}}{\vec h_{t - 1}} + {\vec b_f})$

(8)

${\vec o_t} = \sigma ({\vec U^{(o)}}{\vec x_t} + {\vec W^{\left( o \right)}}{\vec h_{t - 1}} + {\vec b_o})$

(9)

${\overrightarrow {\widetilde {{s_t}}} } = \tanh ({\vec U^{(c)}}{\vec x_t} + {\vec W^{\left( c \right)}}{\vec h_{t - 1}} + {\vec b_c})$

(10)

${\vec s_t} = {\vec f_t} \odot {\vec s_{t - 1}} + {\vec i_t} \odot {\overrightarrow {\widetilde {{s_t}}} }$

(11)

${\vec h_t} = {\vec o_t} \odot \tanh ({\vec s_t})$

(12)

${\overleftarrow{i} _t} = \sigma ({\overleftarrow{U} ^{(i)}}{\overleftarrow{x} _t} + {\overleftarrow{W} ^{\left( i \right)}}{\overleftarrow{h} _{t - 1}} + {\overleftarrow{b} _i})$

(13)

${\overleftarrow{f} _t} = \sigma ({\overleftarrow{U} ^{(f)}}{\overleftarrow{x} _t} + {\overleftarrow{W} ^{\left( f \right)}}{\overleftarrow{h} _{t - 1}} + {\overleftarrow{b} _f})$

(14)

${\overleftarrow{o} _t} = \sigma ({\overleftarrow{U} ^{(o)}}{\overleftarrow{x} _t} + {\overleftarrow{W} ^{\left( o \right)}}{\overleftarrow{h} _{t - 1}} + {\overleftarrow{b} _o})$

(15)

${\overleftarrow{\tilde s} _t} = \tanh ({\overleftarrow{U} ^{(c)}}{\overleftarrow{x} _t} + {\overleftarrow{W} ^{\left( c \right)}}{\overleftarrow{h} _{t - 1}} + {\overleftarrow{b} _c})$

(16)

${\overleftarrow{s} _t} = {\overleftarrow{f} _t} \odot {\overleftarrow{s} _{t - 1}} + {\overleftarrow{i} _t} \odot {\overleftarrow{\tilde s} _t}$

(17)

${\overleftarrow{h} _t} = {\overleftarrow{o} _t} \odot \tanh ({\overleftarrow{s} _t})$

(18)

${h_t} = {\vec h_t} \circ {\overleftarrow{h} _t}$

(19)

其中, 箭头表示处理方向, ${h_t}$ 表示Bi-LSTM的最终隐藏输出, 它由前向输出 ${\vec h_t}$ 和后向输出 ${\overleftarrow{h} _t}$ 连接起来. 我们用Bi-LSTM作为编码器部分, LSTM作为解码器组件, 它通过生成目标值来预测多步时间序列值, 该目标值以先前的时间上下文和先前生成的值为条件. 换句话说, Bi-LSTM编码器负责将输入数据编码到上下文 ${C_T}$ 生成, 它是作为输入数据 ${C_T}$ 的时间表示的一个固定向量. 然后LSTM解码器解码并生成目标序列 $\left( {{f_1},{f_2}, \cdots ,{f_p}} \right)$ 作为多步前向预测值. 目标序列的概率可计算如下:

$p({f_1},{f_2},\cdots,{f_p}|{x_1},{x_2},\cdots,{x_T}) = \prod\limits_{t = 1}^p {p({f_t}|{C_T},{f_1},{f_2},\cdots,{f_{t - 1}})} $

(20)

其中, $\left( {{X_1},\;{X_2}, \cdots ,\;{X_T}} \right)$ 是历史多元时间序列的模型输入, ${x_i}$ 表示时间数据的第 $i$ 个时间步长观测变量, $\left( {{f_1},{f_2}, \cdots ,{f_p}} \right)$ 是多步骤预测的目标值, 其长度 $p$ 可不同于输入长度T(称为查找大小或窗口大小). 如上所述, 我们给出了一个计算结果可使用的经典编码器-解码器的计算过程^[12], 它可对多变量时间序列数据进行建模并完成多步骤预测任务.

1.3 时间注意力机制

标准的编码-解码器深度学习结构在编码时必须将所有编码隐含的过去时态信息压缩成一个固定长度的上下文向量 ${C_T}$ . 而这种编码方式随着输入时间序列长度的增加, 存在前期输入信号被后期输入信号淹没的情况, 进而导致预测能力会逐渐下降. 针对这一难点, 本文首先提出了一种处理时序预测任务的时间注意机制, 并将其连接至编码器和解码器之间. 该框架中使用Bi-LSTM作为编码器, 将时间序列 $x = \left( {{x_1},{x_2}, \cdots ,{x_t}} \right)$ 作为输入, 得到隐含状态 $h$ . 时间注意力层的计算公式如式(21)–式(24):

${e_{it}} = {v'}\tanh ({W_s}{s_{i - 1}} + {W_h}{h_t})$

(21)

${\alpha _{it}} = \frac{{\exp ({e_{it}})}}{{\displaystyle\sum\nolimits_{k = 1}^T {\exp ({e_{ik}})} }}$

(22)

${c_i} = \sum\limits_{t = 1}^T {{\alpha _{it}}{h_t}} $

(23)

${f_i} = g({y_{i - 1}},{c_i},{s_{i - 1}})$

(24)

其中, 式(21)表示解码器层的隐藏状态与编码器层的隐藏状态之间的软对齐计算. 式(22)表示与输入时间序列帧在时间步上的重要性相对应的注意权重, 用于预测在时间步上的输出值, 该方法使用Softmax函数对长度向量进行归一化, 作为输入时间序列上的注意掩码. 式(23)表示为编码层每一个时间步分配相应的权重. 式(24)表示模型解码后的输出值. 模型通过式(25)进行训练.

${e_t} = {\sum\limits_{t = 1}^T {\left\| {{x_t} - {f_t}} \right\|} ^2}$

(25)

2 实验仿真 2.1 数据集构造

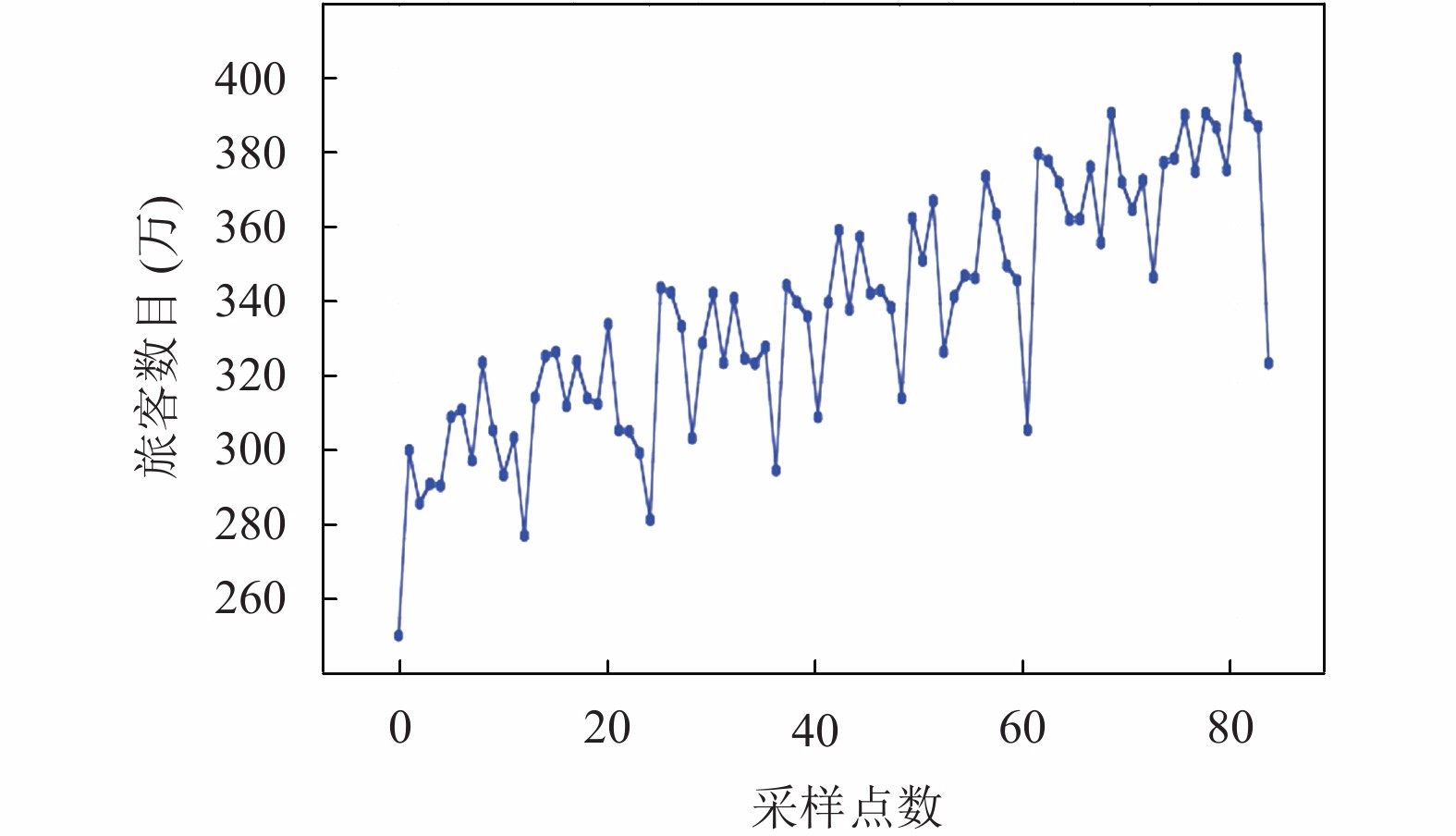
数据源于中国民用航空华东地区管理局官网提供的真实生产运行数据, 选取上海虹桥机场2013–2020年每月客流量数据应用本文算法进行分析, 对其进行可视化, 如图2.

一般来说, 机场客流量的总体趋势受到地区经济发展和结构、人口因素及其构成、地面交通情况以及机场的布局和功能定位等多种因素的影响, 此外更小时间维度上又受季节、天气、大型活动(如节假日)等的影响. 观察图2可以发现, 虹桥机场客流量总体上随着年份呈上升趋势, 且每月的客流量随着季节的不同呈现出一定的周期性趋势, 在冬季客流量偏低.

本文所用样本的构造方法如图3. 首先将数据按照时间顺序进行排列, 然后进行归一化处理, 最后使用滑动窗口的形式进行样本划分. 其中, 输出数据(即标签 $y$ )为该窗口中的最后一个 $N$ 值, 如图3中的 ${y_1},{y_2}$ 所示. 由于本文的实验对象具有时间序列属性, 因此, 为保证输入、输出数据具有连续性; 同时, 为尽量扩大样本数目, 窗口滑动步长选取为 $s = 1$ . 为从时间尺度对模型性能进行测试, 依次将标签长度设置为按照1、3、5三种尺度对样本进行划分, 得到样本集 ${S_1}$ 、 ${S_2}$ 和 ${S_3}$ .

将所构造的样本划分为训练集与测试集, 样本详细描述见表1.

2.2 实验与结果分析

实验使用基于TensorFlow的Keras框架实现模型搭建, 并将其与标准RNN、LSTM分别在 ${S_1}$ 、 ${S_2}$ 和 ${S_3}$ 三个数据集上进行实验对比. 其中, RNN和LSTM经过多次超参数调节, 在权衡最小均方根误差与最小计算机开销情况下, 选择最优的网络结构.

为对模型进行评价, 实验采用平均绝对百分比误差 (MAPE) 与均方根误差作为指标 (RMSE), 其具体计算公式如下:

$MAPE = \frac{1}{n} \times \sum\limits_{t = 1}^n {\left| {\frac{{{P_t} - {R_t}}}{{{P_t}}}} \right|} \times 100{\text{%}} $

(26)

$RMSE = \sqrt {\frac{1}{n} \times \sum\limits_{t = 1}^n {{{({P_t} - {R_t})}^2}} } $

(27)

式中, ${P_t}$ 为模型的预测值、 ${R_t}$ 为真实值. 易知, 上述两种指标值越小则说明模型性能越好, 即预测值越接近真实值.

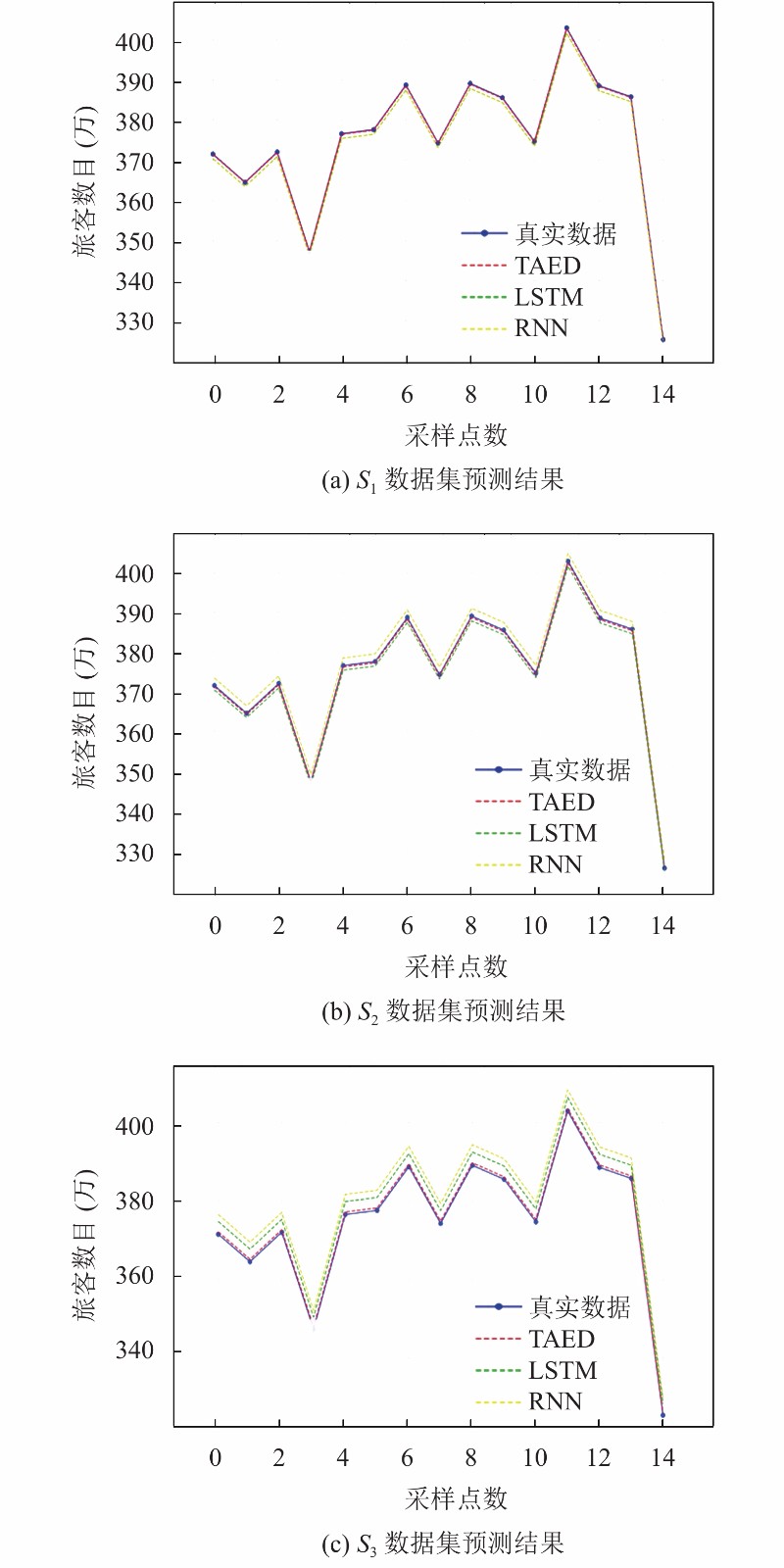
上述模型在3个数据集上进行实验, 测试结果如图4(a)–图4(c), 误差指标见表2.

通过对图4(a)–图4(c)对比可知: 由于数据集 ${S_1}$ 进行的是单步预测, 因此模型均能够对机场客流量进行准确预测, 虽然RNN相对于LSTM与TAED误差较大, 但预测值与真实值基本保持在可容忍范围内. 在数据集 ${S_2}$ 中, 对于时间步的预测增加到3步, 可以看出相对于数据集 ${S_1}$ , 3种模型的性能均有所下降, 其中, TAED模型性能下降程度最小; 在数据集 ${S_3}$ 中, 将时间步的预测增加到5步, RNN和LSTM一定程度上偏离真实值, 而TAED模型仍能够保持较好的性能, 这是由于该模型能够通过调整不同时刻输入值对输出值的贡献来进行预测. 同时, 根据表2对于残差的计算结果可以看出, TAED模型在3个数据集上的表现明显优于RNN和LSTM, 且多步预测中效果更为明显, 如在数据集 ${S_1}$ 和数据集 ${S_3}$ 上, TAED模型的平均标准误差分别比LSTM低了57.9%和78.4%.

3 结论

机场客流量预测对于机场调度安排, 制定运行计划具有重要意义. 由于机场客流量数据具有强时序特征, 而传统方法如LSTM、RNN难以有效提取数据的时间依赖特征. 本文提出一种基于注意力机制的编码解码模型, 并对虹桥机场客流量数据进行仿真实验, 结果表明: 通过对编码解码模型引入注意力机制, 使得模型能够对历史数据特征进行充分提取, 从而在单步预测与多步预测上均表现出较高的精度. 虹桥机场客流量主要受到地区经济发展等各类因素的综合影响, 不同类型的机场客流量影响因素略有差异, 主要包括贸易、人口、资源、环境等, 但不同类型机场的历史数据特征是可以学习的, 因此本文方法对于不同类型的机场客流量预测具有普适性. 同时, 本文未考虑影响机场客流量的相关因素, 今后的工作中, 可以通过引入准点率等相关因素, 从更多维度对客流量进行预测.