流场可视化是科学可视化的重要研究方向, 帮助优化和理解复杂的科学、工程等流体模拟与观测数据, 因此广泛应用于气候建模, 空气动力学, 湍流燃烧、计算流体力学等领域研究中. 基于积分计算的流线可视化方法是最常用的揭示流场特征走向的方式, 它是流场的一种稀疏表示^[1]. 流线的计算需要先在放置种子点, 再根据向量场计算种子点的轨迹路径, 轨迹计算需要采用数值估计的方法求解, 如龙格库塔法^[2].

流线可视化的质量很大程度上影响了对于流场形态与特征的理解, 过少的流线可能会遗漏流场重要的特征, 但过多的流线会产生计算浪费, 同时具有遮挡、聚集等问题. 因此关于如何合理放置种子点的研究也是流场可视化的热门方向, 其目标是在少量的计算下尽可能地去准确覆盖展示流场^[3-7]. 另一方面基于交互的选取种子点的方式可以给予用户更多的自由度去控制生成的可视化结果, 从而帮助用户更快的探索和了解流场信息. 但由于流线生成的计算代价非常大, 现有方法多在大规模集群机器的计算支持下, 通过并行计算的方法来生成大量流线^[8], 这种方式会受到设备计算能力的限制, 给用户带来不便.

对于大规模流场, 用户难以需要获取全部数据, 因此实时了解流场数据情况, 可以帮助用户快速选择所需区域进行后续分析. 目前的流场可视化系统常采用并行计算的方式加速粒子追踪, 对计算资源的需求较高, 单机的实时性较差, 且需要存储整个流场数据. 而许多相关研究学者并没有集群计算设备的支持, 从而大大降低了可视化系统的效率和交互性. 缺少轻量级的交互可视化系统, 给用户快速了解流场整体情况提出了较大挑战, 除感兴趣区域外, 用户需要保存大量冗余数据, 影响进一步深入研究, 降低研究效率.

为此, 本文基于深度学习方法设计了流线的超精度重建算法, 通过对于流线进行超精度提升的方式, 极大地降低了流线的计算量, 以此实现流线实时的可视化生成, 使得用户在交互的同时, 可以实时查看对应的高精度流线结果, 提升用户对于大规模流场的探索效率, 且避免了对大规模计算资源的需求. 此外, 可视化系统也对流场进行多维度信息展示, 显示其对应的特征分布与属性信息, 为研究人员提供可靠的流场可视化分析与特征分析, 提高研究效率.

本文的主要贡献如下:

(1) 提出基于深度学习高精度流线映射算法, 可将流场中稀疏的低精度流线映射为高精度流线, 避免大量的积分计算.

(2) 设计交互式流场可视化系统, 帮助用户实时观测流场特征, 快速探索流场数据.

(3) 通过界面中多个视图的数据联动及交互, 多维度展示流场信息, 进行特征分析.

1 国内外研究现状 1.1 流线放置算法

流线一般通过数值积分法绘制, 流线上处处与速度场相切, 对于流线 ${x_s}: R \to {R^d}$ 和向量场 $V:{R^d} \times $ $ R \to {R^d}$ , 有:

$\left\{ { \begin{array}{l} \dfrac{{{{d}}{x_s}(s)}}{{{{d}}s}} = V({x_s}(s))\\ {x_s}(s) = {x_s}({s_0}) + \displaystyle\int_{{s_0}}^s {V({x_s}(\tau )){{d}}\tau } \end{array} } \right.$

(1)

生成有代表性的流线去有效表示流场一直是流场可视化的重要研究方向. 算法主要可分为3类: 基于密度、基于特征和基于相似度计算^[9].

基于密度的方法会倾向于生成一个统一分布的流线来描述整个流场. Hultquist等^[10]首先提出通过保持流线之间的距离来放置种子点. Jobard等^[11]通过设置阈值距离 ${d_{\rm{sep}}}$ , 使得每一个候选种子点都在现有流线的阈值外, 且当积分流线进入现有流线的阈值范围时, 停止流线计算. Turk等^[12]将流线能量量化为函数形式, 并通过低通滤波器将能量优化为最小值来得到最优的流线集合.

基于特征的算法更倾向于将种子点放置在流场的特征区域(如临界点位置)来覆盖用户可能的感兴趣区域. Verma等^[13]提出了一种基于临界点的放置模板来捕捉流场的行为特征, 通过Voronoi图将流场分为包含相似特征的区域并放置种子点. Liu等^[14]提出了一种均匀分布的流线算法(ADVESS), 通过双对列的方法来对Verma等^[13]所生成的后选种子点进行补充.

基于相似度的算法会计算流线间的相似性并从中选出有代表性的流线. Chen等^[15]首先提出了相似距离度量的方法来减少并行相似流线, 包括计算最近点的欧拉距离和流线走向. Hong等^[16]提出层次化的流线捆绑算法, 使用MCPD^[17]来作为流线的相似性度量, 自底向上地合并相似的流线直到达到停止条件.

1.2 基于深度学习的科学可视化

随着深度学习在许多领域应用的巨大进步和成功, 在科学可视化领域, 应用深度学习算法解决传统问题的研究越来越多.

其中, Hong等^[16]提出基于LSTM的方法预测粒子追踪所要用到的数据块, 从而达到计算的负载均衡. Han等^[17]通过将生成流线进行自编码的方式达到对流场数据的约简. He等^[18]提出基于深度学习的算法对集合可视化的参数空间探索. 也有部分工作研究关于科学数据的超精度算法, 如Han等^[19]提出对时变数据进行时间上的超精度提升, 而Zhou等^[20]和Guo等^[21]分别对体数据和向量场数据进行空间超精度生成. 但关于流线数据的超精度生成尚未被研究过, 同时也是这篇工作的主要内容.

1.3 交互流场可视化系统

交互流场可视化已经有20年的发展历史, 其可以给用户更多的自由度去控制生成的可视化结果.

Schulz等^[22]提出了对于车身空气动力学模拟进行可视化的交互系统, 并且通过优化数据结果与插值方法提升了粒子追踪效率. Laramee等^[23]开发了一种手工放置种子点的工具, 并向用户提供了多种交互方式, 可以对种子点平面进行旋转、平移、缩放等操作. Laramee^[24]也开发了另外一个交互系统Streamrunner, 来解决3D流线可视化的遮挡问题.

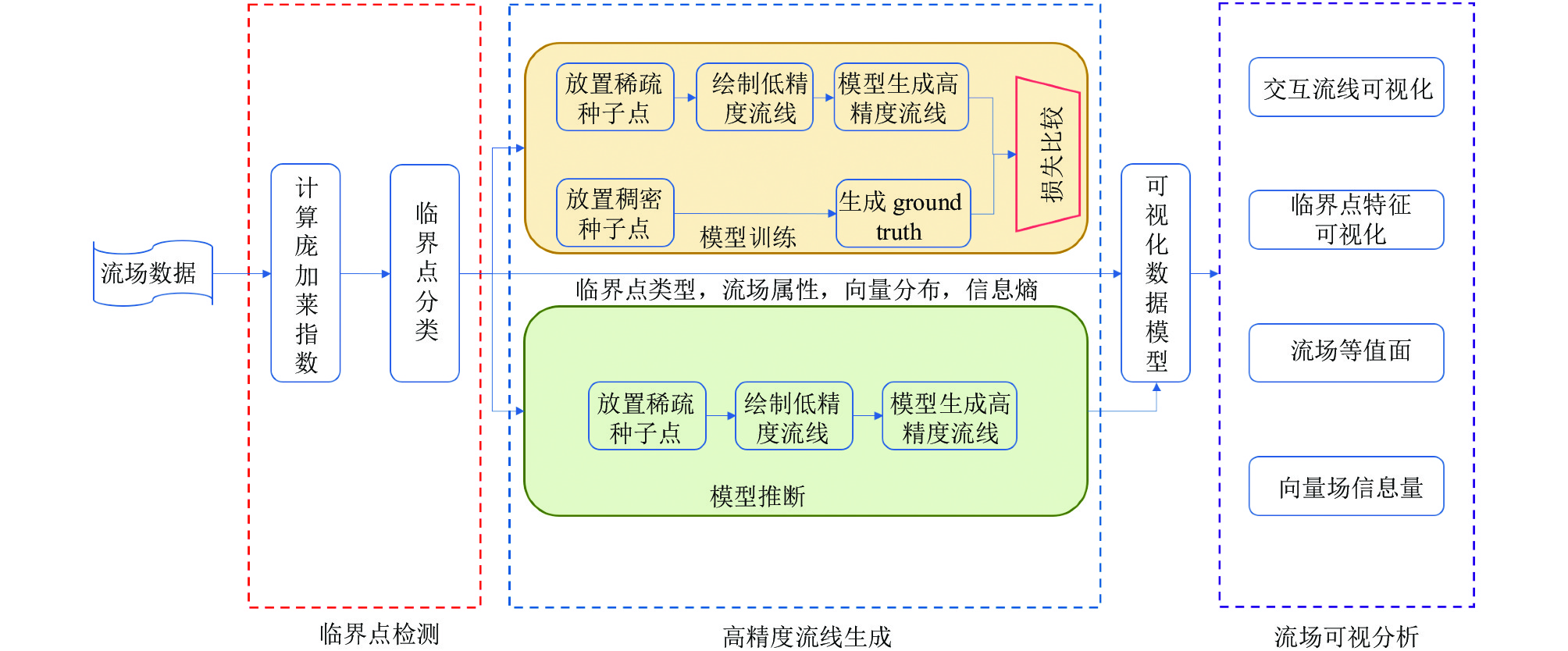
2 系统流程设计

实时流场可视化系统(如图1) 主要由3部分组成: 临界点检测模块, 高精度流线生成模块, 流场可视分析模块. 临界点检测模块基于Poincarre Bendixon指数, 在检测流场临界点的同时标记了临界点类型, 便于后续进行统计分析. 高精度流线生成模块包含算法的主要内容, 包括模型的训练阶段和推断阶段: 在训练阶段, 在临界点处放置种子点生成训练数据对来计算损失并进行反向传播, 优化模型参数; 而在推断阶段, 直接放置稀疏种子点进行粗粒度的快速流线绘制(如将最小步长设为2个网格长度), 后由模型生成高精度流线, 得到更精细稠密的流线可视化效果. 流场可视分析模块整合之前的所有数据后, 提供给用户可交互的呈现和探索方式, 便于用户快速了解流场结构及特征信息. 系统工作流程如流程1所示.

流程1. 基于高精度流线生成的交互可视化

1. 快速临界点检测;

2. 在临界点处放置初始稀疏种子点;

3. 基于稀疏种子点采用龙格-库塔法进行粗糙的流线追踪计算, 此时追踪步长较长, 可以快速完成流线计算;

4. 将粗糙流线集合 $\scriptstyle {{\textit{S}}_{\textit{L}}}$ 输入深度学习MUSE模型, 完成模型的推断过程, 输出稠密的高精度流线集合 $\scriptstyle {{\textit{S}}_{\textit{H}}}$ ;

5. 返回流线 $\scriptstyle {{\textit{S}}_{\textit{H}}}$ 进行绘制, 同时提供多种交互方式帮助用户选择时空区域和绘制属性.

3 高精度流线生成算法 3.1 算法及任务概述

对于流场内流线的高精度生成问题, 我们将其定义为序列数据的多步回归任务, 即对于流场区域 $V$ , 我们有初始放置的稀疏种子点集合 ${P^0} = \{ p_1^0,p_2^0, \cdots ,p_m^0\} $ , 基于这些稀疏种子点, 进行粗粒度的快速流线积分计算, 可得到稀疏的流线集合 ${S_L} = \{ s_1^L,s_2^L, \cdots ,s_m^L\} $ 作为算法的输入数据, 其中 $s_i^L = \{ p_{i1}^L,p_{i2}^L, \cdots ,p_{i{d_l}}^L\} $ 为第 $i$ 条流线上点的集合, 每条流线长度为 ${d_l}$ . 经过神经网络模型映射, 我们可得到稠密的高精度流线集合 ${S_H} = $ $ \{ s_1^H,s_2^H, \cdots ,s_n^H\} $ , 且每条流线 $s_i^H = \{ p_{i1}^H,p_{i2}^H, \cdots ,p_{i{d_h}}^H\} $ 长度为 ${d_h}$ , 其中, ${d_h} > {d_l}$ , 且 $n > m$ .

神经网络由于其特有的非线性映射特性, 已经在多个研究任务和领域内被证实其学习复杂依赖的能力. 传统的插值或回归算法, 如线性插值或ARIMA模型都假定数据之间线性依赖关系, 无法进行非线性映射. 同时, 插值等方法往往只能处理单变量数据, 当流场内需要进行多条流线数据的高精度生成时, 无法同时处理, 也就无法学习到流线之间的空间关系. 近年, Transformer^[25]在序列学习任务中被广泛使用, 其仅依赖attention机制去捕捉输入序列的全局依赖性, 避免了RNN模型中需要反复循环计算的限制, 大大提高了模型效率. 然而也有研究者提出Transformer由于采用自注意力机制在处理长跨度依赖时收效甚微. 因此, 我们采用MUSE (MUlti-ScalE attention)模型^[26], 其将卷积操作与注意力机制结合, 提出了并行多尺度计算的注意力模型.

MUSE同样使用encoder-decoder结构, encoder将一个序列数据 $\left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}$ 作为输入, 将其编码为隐向量表示 $z$ , 而decoder用来生成输出序列 $\left\{ {{y_1},{y_2}, \cdots ,{y_n}} \right\}$ 作为模型结果. 算法核心为MUSE模块, 如图2所示, 其包括3个主要部分: 自注意力机制 (self-attention)用来捕捉全局特征, 深度可分离卷积 (depth-wise seperable convolution) 来捕捉局部特征, 和一个基于位置计算的前向网络来捕捉单个输入的特征. 模块接受上一层 $i - 1$ 的输出作为输入, 输出可表示为:

${X_i} = {X_{i - 1}} + Attention({X_{i - 1}}) + Conv({X_{i - 1}}) + Pointwise({X_{i - 1}})$

(2)

模型的encoder是由多层MUSE模块组成, 并采用了残差学习机制和归一化层 (layer normalization). Decoder也具有相似的结构.

同时交互流场可视化系统对实时性要求较高, 由于MUSE操作的可并行性, 大大提高了计算速率, 加速了模型的推断时间, 使得应用时可以快速生成大量流线数据.

首先, 将稀疏的流线集合 ${S_L}$ 输入模型, 经过多层MUSE模块组成的encoder进行编码, 再由decoder在输出层输出高精度流线集合 ${S_H}$ . 本算法在与原始高精度流线数据比较中可达到较高的准确性, 并且提高了高精度流线生成的效率, 增强交互可视化的实时性.

3.2 数据集生成

数据集可分为训练集和测试集, 其中训练数据对包含输入的稀疏流线与输出的稠密流线. 对于每个流场, 首先进行基于Poincarre Bendixon参数的临界点检测, 对于不同的临界点类型, 采用Verma等^[13]的种子点模版放置稠密的种子点, 如图3所示.

对该模板生成的稠密种子点进行精细的流线计算, 可得到高精度的流线真值 ${S_H}$ 作为模型所需的训练输出; 在此基础上, 对于流场中每个临界点区域, 求出第一步生成的种子点的中心, 作为稀疏的种子点集合, 并进行粗粒度的流线计算, 得到点数远小于上述精细流线的粗糙流线 ${S_L}$ , 作为模型的训练输入, 以此作为模型的训练数据对.

3.3 损失函数

对于模型所生成的高精度稠密流线集合 ${S'_H}$ , 我们有真值的流线集合 ${S_H}$ , 在训练过程中, 为了保证模型输出能够更接近于真值, 我们采用流线上点坐标的均方差损失MSE作为我们训练模型的损失函数, MSE定义为:

$\mathcal{L} = \sum\limits_N {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{{d_h}} {||{p_{ij}} - {{p'}_{ij}}|{|_2}} } } $

(3)

其中, ${p_{ij}} \subseteq s_i^H$ , ${p'_{ij}} \subseteq s'{_i^H }$ 分别为真实和预测生成的第 $i$ 条流线中的第 $j$ 个点, $N$ 为训练样本数, $ {\Vert \rm{ } \cdot \rm{ }\Vert }_{\rm{2}}$ 为 ${L_2}$ 范数.

4 交互式可视化系统 4.1 可视化系统介绍

本文在基于深度学习的流线高精度生成基础上, 开发了包含流线绘制, 统计信息展示的交互流场可视化系统, 通过不同视图之间的数据联动, 对流场所具有的临界点位置分布, 特征属性分布, 统计信息以及流场结构进行交互可视化展示, 用户可通过交互选择感兴趣的时空区域, 自由生成所需的可视化结果, 了解流场目标区域的特征信息, 提高用户对流场数据分析效率, 避免获取到大量不需要的冗余数据. 系统可满足用户不同的分析需求:

(1) 选择流场内某一区域进行流线可视化, 展示流场特征结构分布.

(2) 查看当前时刻流场, 或选择区域内流场的临界点个数, 及统计对应类型分布.

(3) 查看流场自身属性及信息量信息.

4.2 可视化属性选择

本文所用到的流场及临界点属性如下:

(1) 涡度

涡度 $\vec \zeta $ 是速度场的旋度, 可以用来描述流体的旋转情况.

$\begin{split} \vec \zeta = &\nabla \times \vec v \\ =& \left( {\frac{{\partial w}}{{\partial y}} - \frac{{\partial v}}{{\partial {\textit{z}}}}} \right)\vec i + \left( {\frac{{\partial u}}{{\partial {\textit{z}}}} - \frac{{\partial w}}{{\partial x}}} \right)\vec j + \left( {\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}}} \right)\vec k \\& \end{split} $

(4)

(2) 流线曲率

流线曲率可以用来描述流线的弯曲程度^[27].

$c = \frac{{v \times a}}{{{{\left| v \right|}^3}}}$

(5)

其中, $a$ 为局部加速度, 为Jacobian矩阵与速度的乘积.

$a = (\nabla v)v$

(6)

(3) 扭矩

扭矩可以表现流线的扭转程度^[27].

$\tau = \frac{{\left( {v \times a} \right) \cdot ((\nabla a)a)}}{{{{\left| {v \times a} \right|}^2}}}$

(7)

(4) 向量场信息熵

对于任意的变量 $x \in \{ {x_1},{x_2}, \cdots ,{x_n}\} $ , 如果我们知道取值的概率 $p({x_i})$ , 我们可以计算其包含的信息熵.

$H(x) = - \sum\limits_{{x_i} \in X} {p({x_i}){{\log }_2}p({x_i})} $

(8)

将其应用的向量场, 我们首先对向量进行分桶, 得到其对应的直方图, 这样, 对于每一个在桶 ${x_i}$ 内的向量, 可以计算它取值的概率为:

$p({x_i}) = \frac{{C({x_i})}}{{\displaystyle\sum {_{i = 1}^nC({x_i})} }}$

(9)

其中, $C({x_i})$ 为桶 ${x_i}$ 内的向量个数. 这样, 我们可以用式(7)计算得到向量场的信息熵^[28].

4.3 可视化设计(视图介绍: 需求+设计/交互+作用)

图4展示了流场交互可视化系统的设计视图, 系统的流场可视化主要有4个部分组成: 高精度流线可视化, 流场速度量和旋度量等值面视图, 向量场信息量视图, 临界点特征统计图. 各个部分可以通过用户选取不同的时间和空间区域进行联动变换, 用户可以通过上方的时间轴选择不同时刻的流场, 不同视图从各个维度展示流场信息.

4.3.1 高精度流线可视化

流线可视化视图展示了当前选择区域的高精度流线, 流线围绕在临界点区域, 由第2节所述算法生成. 如图4(a)所示, 我们在展示高精度流线的基础上, 用户可以使用上方的时间轴组件选择不同时间的流线进行展示, 同时可以使用鼠标对视图内的流线进行拖拽, 变化观察角度, 或者放大缩小当前视图, 对局部进行观察.

4.3.2 流场等值面视图

如图4(b)所示, 流场等值面视图是对了流场中所具属性进行等值面绘制, 如速度量和涡度量, 并以颜色框形式将识别出的临界点进行标注, 用户可通过选择不同属性的等值面, 了解流场区域的某一属性的整体分布情况. 我们将属性分为标量值(如盐度等)和向量的大小(如速度量). 同时, 视图可以提供关联分析, 了解某一属性与临界点位置及数量的关系.

4.3.3 向量场信息量视图

向量场信息量视图描述出流场内的不确定性及向量极角值的分布情况. 如图3(c)所示, 当前流场区域的信息熵会以下方折线图形式展示, y坐标轴是对应的时刻. 用户点选某一时刻时, 该时刻在折线图上被标记高亮, 同时上方展示该时刻的向量直方图, 采用极性坐标直方图的形式, 向量依据极角被分进60个桶内进行数量统计, 用户可以观测到不同极角值下向量的数量分布情况.

4.3.4 临界点特征统计视图

如图4(d1) 所示, 通过极坐标热力图, 按天数展示了流场内临界点个数分布的变化情况. 可以快速看到不同临界点类型在整个时间范围内的分布.

同时, 如图4(d2) 所示, 临界点特征统计视图对当前所选流场区域内在不同时刻的临界点类型及对应个数进行了统计, 临界点类型包括鞍点, 螺旋/中心和交点, 分别用不同的颜色表示. 视图采用堆叠柱状图形式, x坐标轴代表流场的时刻, y坐标轴为临界点个数, 临界点总数以折线形式展示. 用户可以通过下方时间轴选择某一范围内的时刻进行展示, 通过鼠标悬浮, 用户可以得到具体的临界点数量. 通过时间线的横向比较, 用户可以查看流场内特征情况的变化趋势.

5 实验分析 5.1 实验数据集

本文采用的数据集如表1所示, 其中, Smoke数据集由烟雾模拟程序生成^[29], 分别进行了二维和三维的模拟, 每一个模拟可以产生200个时间步长. 红海数据集来自Scivis Contest 2020发布的比赛数据集, 涵盖了一个月的红海海域模拟数据, 区域范围为30°E–50°E, 10°N–30°N, 空间分辨率为0.04°×0.04° (4 km), 其本身是三维数据, 深度为50, 由于海洋流场运动多为平流运动, 我们对其从z轴方向进行了数据切片, 生成实验数据.

5.2 模型结构及训练

我们将基于PyTorch实现MUSE模型, 采用多头注意力模型^[25]作为我们的自注意力模型, 注意力头数为4, 模型包含12个残差模块作为编码器, 对应的有12个残差模块作为解码器, 隐藏维度为1024. 我们在两个NVIDIA GTX 1080Ti GPU上进行模型训练, batch设为32, 对于单个卷积核, 核大小为7, 对于动态卷积核, 核大小为3. 初始学习率为0.001, 采用warmup机制来调整学习率, warmup更新率为4000.

5.3 评价指标

对于第2节中所提到的高精度流线生成算法, 我们采用MCPD (Mean of the Closest Poiny Distancing) 来比较其与原始高精度流线之间的距离误差.

MCPD常用来作为轨迹线之间的相似性度量, 对于其中一条流线, 计算其每个点到另外流线上最近点的距离并求平均.

$MCPD({S_i},{S_j}) = mean({d_m}({S_i},{S_j}),{d_m}({S_j},{S_i}))$

(10)

其中, ${S_{i(j)}}$ 为一条流线, 即一组点 ${p_{k(l)}}$ 的集合, 且有:

${d_m}({S_i},{S_j}) = mea{n_{{p_k} \in {S_i}}}\mathop {\min }\limits_{_{{p_l} \in {S_j}}} \left\| {{p_k} - {p_l}} \right\|$

(11)

MCPD越小, 流线越相近.

而为了衡量所生成流线对于原始流场的代表性与描述准确性, 我们采用量化方式评价流线质量, 即通不同方式生成的流线去重建向量场. 如果流线可视化成功展示了流场内的大部分信息, 那么所重建的流场应该具有较小的误差^{[26, 29-31]}.

我们使用Gradient Vector Flow (GVF) ^[32]来重建向量场, 其使用高斯平滑权重且不断迭代优化向量场直至扩散方程收敛.

PSNR(Peak Signal-to-Noise Ratio)衡量了流场中每个坐标点上向量之间的平均误差. 通过比较生成向量场与原始向量场的PSNR, 我们可以有效评价流线质量.

$PSNR(v,v') = 20{\lg}MAX(v) - 10{\lg }MSE(v,v')$

(12)

其中, $MAX(v)$ 是向量场中最大值与最小值的差.

越高的PSNR代表两个流场越相近, 即重建的准确率越高.

由于PSNR只针对衡量向量场中单个向量之间的误差, 无法评价流场之间特征情况的差距, 为此, 我们定义了一个新的评价指标CPd, 即对重建的向量场再次进行临界点检测, 与原始流场中的临界点进行对比分析, 求出对应临界点的距离, 作为定量评价标准之一, 流场之间的误差CPd即为流场内临界点距离的和并对临界点个数进行规范.

$CPd(v,v') = \frac{{\displaystyle\sum\nolimits_{i{\rm{ = 1}}}^N {||{c_i} - {{c_i'}}||} }}{{\max ({N_c},{{N_c'}})}}$

(13)

其中, ${c_i}$ 和 ${c'_i}$ 为原始流场与重建流场中对应的临界点, 若没有找到对应点, 则距离定为1, ${N_c}$ 和 ${N'_c}$ 为对应的临界点个数.

5.4 结果分析

为了衡量高精度流线生成算法的准确性与高效性, 我们将线性插值方法作为比较的baseline, 并与原始经过积分计算的高精度流线进行比较分析, 分别从定性与定量角度, 从精确度、还原性与时间效率评价算法模型.

5.4.1 定量分析

如表2所示, 我们将生成的高精度流线与初始计算的低精度流线所重建的向量场进行对比分析, 可以看到, 高精度流线对于原始流场的涵盖更高, 描述更准确, 因此通过流线重建的向量场从PSNR与CPd指标上与原始向量场更为接近, 这也说明了高精度流线生成的必要性, 可以向用户更准确的描述流场.

此外, 我们也对比了插值方法生成的高精度流线与MUSE模型所生成的高精度流线的对应指标. 可以看出, 模型的生成的流线与原始高精度流线更为接近, MCPD更小. 通过流线重构向量场, 比较与原始向量场的PSNR与CPd指标, 可以看到, 相比于线性插值方法, 模型所得到的向量场更加接近原始向量场, 检测到的临界点位置也更加准确.

如表3所示, 我们对比分析了模型生成流线与采用龙格库塔4.5阶积分运算的时间效率与种子点个数的关系.

从表3中可以看出, 由于MUSE继承了Transformer可并行的优势并进行了并行计算优化, 且由于流线为模型一次性全部输出, 模型的推断时间与流线密度关系不大, 因此, 种子点个数越多, 深度学习模型的效率优势越大.

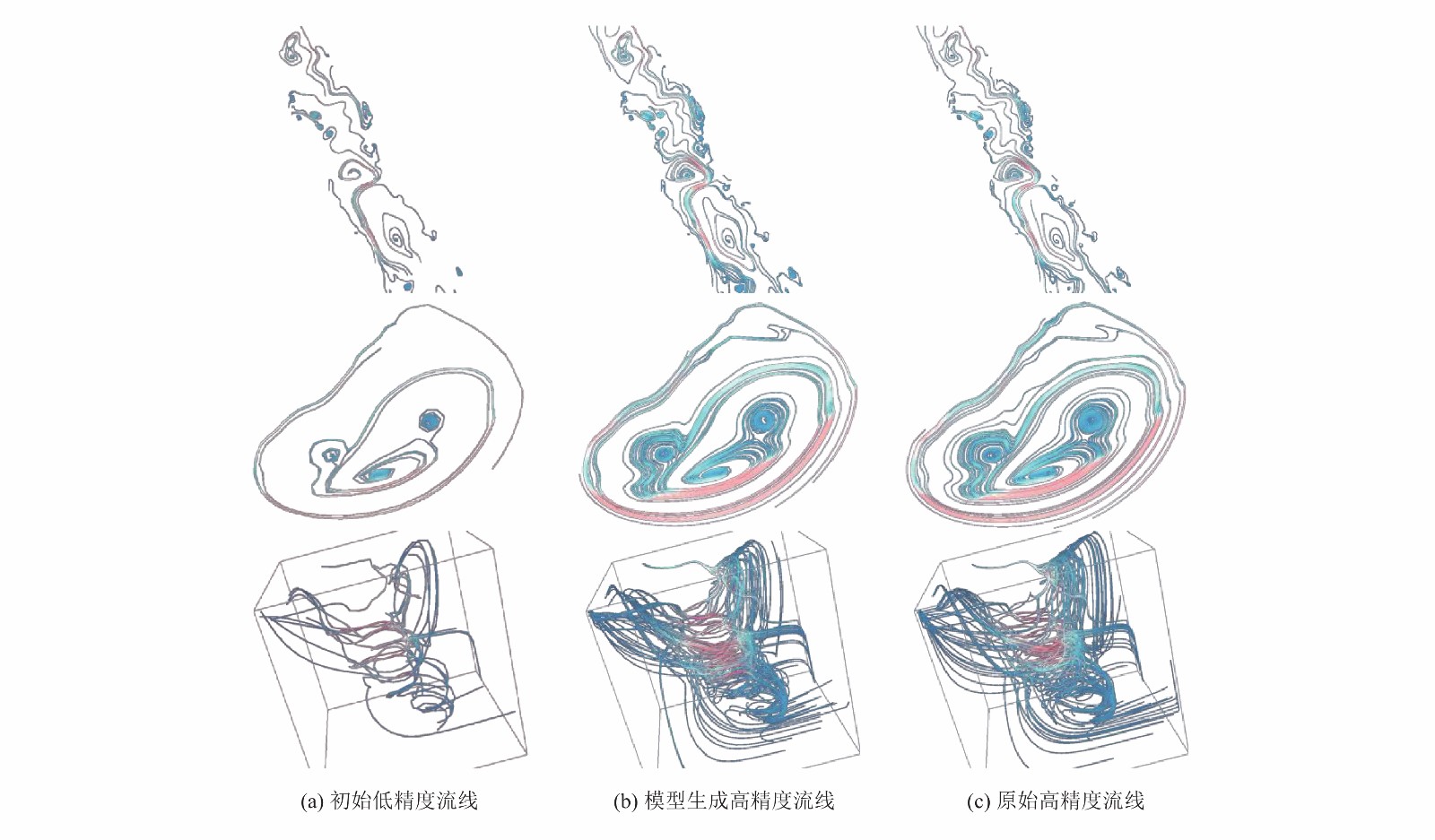
5.4.2 定性分析

图5对比展示了初始计算的低精度流线, 模型所生成的流线, 和原始高精度流线结果. 从上到下依次为红海海域局部流场数据, 二维烟雾流场数据与三维烟雾流场数据.

可以看到, 从流线可视化的角度来看, 在3个数据集上, 尽管模型所生成的流线仍具有一定的粗糙性, 但都能够较为准确的还原出原始的高精度流场及对应的特征. 且由于种子点增多和流线精度提升, 相比于低精度流线, 模型生成的高精度流线对于流场特征的描述更为准确和清晰, 如在红海海洋流场数据中, 一些低精度流线没有很好展示的螺旋结构和鞍点结构, 在高精度流线中都能够被很好地还原.

6 可视化案例分析

基于本文所提的流场可视化交互系统, 选择红海数据集对红海海域进行可视化分析, 多维度分析其流场特征.

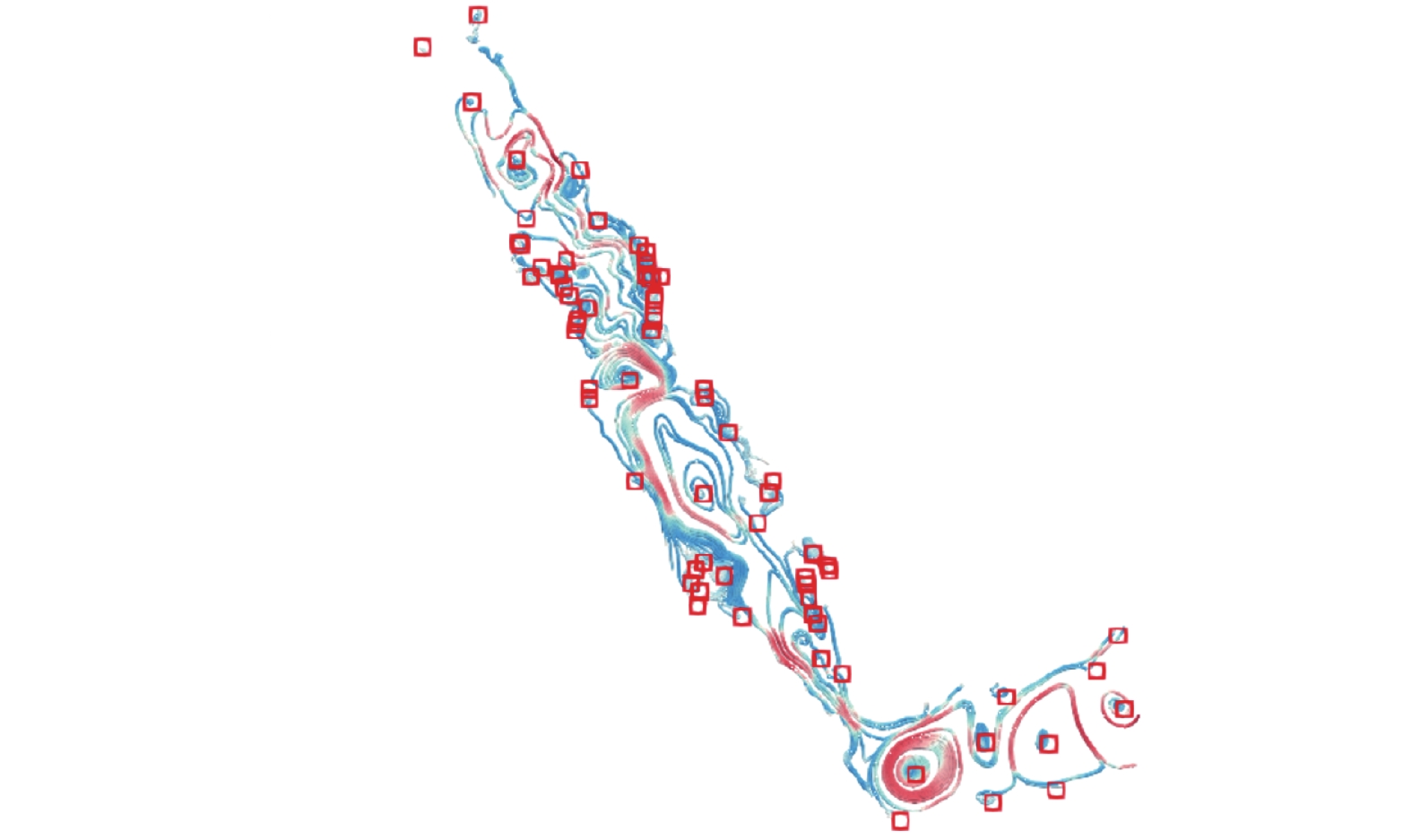
6.1 高精度流线可视化

图6显示了红海海域的切片流线可视化结果, 颜色由速度量进行渲染, 并由红色框圈出流场内临界点位置, 用户可以点选选择不同深度的切片流场, 或者通过鼠标拖拽操作选择某一区域的流场进行流线绘制.

从高精度流线与关键情况可以看出, 红海海域的涡旋(即临界点)更多的分布在海岸附近, 尤其是红海北部涡旋数量更多. 而南部的亚丁湾区域, 涡旋分布数量较少, 但可以从流线看出涡旋结构都较大, 包含有3个较大的螺旋涡, 以及分布在周围的鞍点区域.

6.2 流场属性等值面分析

根据流场的不同属性可以进行等值面绘制, 由于海洋流场数据的特殊性, 用户可以选择查看其速度, 涡度大小的等值面, 也可以查看温度、盐度的等值面数据. 如图7所示, 图7(a)–图7(d)分别为海洋流场的盐度、温度、速度量、涡度量的等值面绘制, 临界点在图上被圈出, 临界点的颜色由该位置的速度量进行映射, 用户可以观察到流场中不同属性的分布情况, 及其与临界点生成的相关性.

从图7(a)可以看出, 红海海域北端, 即苏伊士湾区域和亚喀巴湾区域盐度更高, 且红海整体海域越靠北等值面颜色越深, 即盐度越高; 从红海的中部海域可以看出, 海岸边盐度要高于中心盐度, 对应的关键数量也更多; 而南部的亚丁湾海域盐度较低, 根据其颜色深度的分布情况也可以看出明显的涡旋结构, 说明洋流中盐的浓度迁移与洋流或湍流运动具有极大的相关性, 气旋涡.

从图7(b)中可以看到海域的温度分布, 红海海域的北端和南端温度都较低, 而中部的温度较高. 且中间东部海域要比西部海域温度更高. 从温度的等值面绘制中也可以可看到一些涡旋结构与临界点位置正好对应, 例如, 在气旋涡作用下, 将海底冷流带入上方暖流, 使得涡旋内部温度相比于周围更低, 在反气旋涡的作用下, 将暖流传递到下方冷流, 使得涡旋内部温度较高.

图7(c), 图7(d)分别为海域的速度值与涡度值得等值面映射, 可以看到, 涡度较高的位置会有临界点的分布, 此时的流场得旋转程度更高, 更容易形成螺旋/中心圆形状的临界点特征.

6.3 流场信息量分析

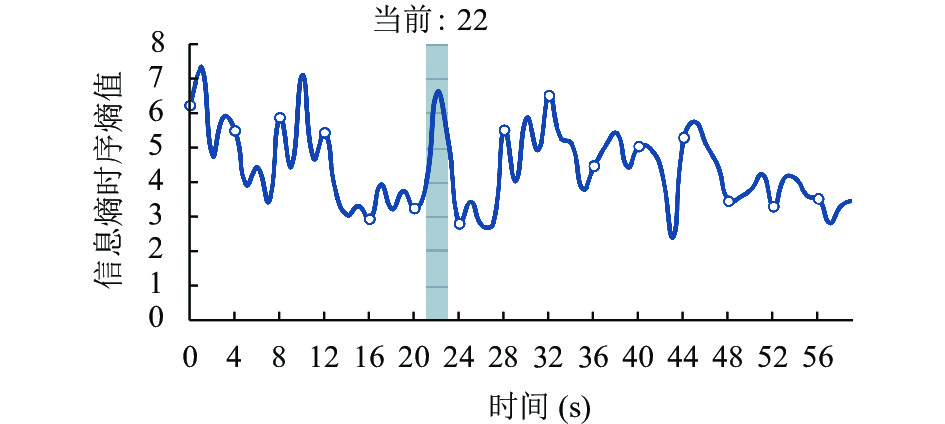
图8展示了流场内向量信息熵随时刻的变化情况, 可以看到, 流场整体信息包含量有随时间逐渐减少的趋势, 但同时也会有波动震荡, 整体信息熵在2–8之间.

图9展示了流场内向量的分布情况, 为更好地分析其与流场特征结构的关联, 我们将其与高精度流线视图并列展示. 可以看到, 流场内具有临界点特征时, 流场向量更倾向于具有较多变化性, 即直方图更倾向于呈现均匀分布的特征, 对应的熵也就越大.

6.4 临界点特征分布

为对所选流场内的临界点特征信息进行量化展示, 图10展示了流场内临界点类型及对应个数分布随时间变化的趋势. 可以看到, 随着时间的演变, 临界点数量呈现一个先减少后增多的趋势. 且从堆叠柱状图上可以看到, 相比于鞍点和螺旋结构的临界点, 交点结构的临界点区域较少, 而螺旋结构的临界点数量较多.

7 结论与展望

文本将深度学习中进行序列映射学习的MUSE模型应用到流线的高精度生成任务中, 避免了大量的粒子追踪积分计算, 大大提高流线生成的效率, 同时相比于简单的线性插值计算, 生成流线更接近于原始流线, 且对向量场描述更加准确. 在此基础上, 使用算法生成的高精度流线, 结合流场特征检测, 信息论分析等方法, 开发了流场实时交互可视化系统, 用户可通过交互选取所需时空域快速查看流场信息, 了解流场特征, 帮助用户选择自己所需的数据进行后续进一步深度分析. 本文使用Scivis Contest 2020所提供的红海海域流场及属性信息作为案例, 展示了系统对于流场结构, 特征分布, 信息量分析等多维度关联分析的高效性与准确性, 验证了系统可以有效对于大规模流场进行快速实时的可视化说明与分析, 提高用户的工作效率, 简化复杂的分析流程.

本文的工作局限于对于流场的流线可视化, 需要对不同时刻的流场进行多次流线计算, 增加了数据读取的I/O操作, 之后, 我们可以考虑进行迹线的分析与高精度生成, 进一步提高可视化效率, 提供更多的交互分析操作, 帮助用户了解流场的时序变化情况. 另一方面, 本系统可以用于原位可视化中对于数据模拟的实时监督, 帮助用户了解当前模拟数据情况, 是否产生模式坍塌, 以及是否要及时停止模拟. 这样, 就需要进一步提高系统的数据读取速率, 结合多分辨率的数据结构来优化系统效率.