目前, 我国物流业发展的特点之一是智慧物流进入创新爆发时期, “互联网+智慧仓储”等创新模式迅速发展. 人工智能技术已经融入到了物流行业的生产仓储环境中, 智慧仓储物流设备的使用大大节省了人力资源, 充分发挥机器换人、货物找人、可视管理的运行理念, 遵循依托物联网与智能算法, 进行物流仓储的全流程自动控制的核心思想, 通过生产物流的信息化、快速、高效、可追溯性, 实现真正智能化. 智慧仓储物流通过依托物联网与智能算法, 进行全流程自动控制, 实时、有效地管理物流, 提供更具社会价值的物流效应^[1]. 中国作为生产大国, 智慧物流为大势所趋.

智慧物流调度设计的关键是要满足系统订单货物运送的要求, 满足客户、AGV和云技术之间动态协作的需求以及满足物流仓储的实际操作需求. 高效率和一致性是智慧物流调度系统的关键. 在智慧仓储中, 货物被放在可以移动的货架上, 用来进行货物运送工作的自动引导车(Automated Guided Vehicle, AGV)是一种先进的自动化物流设备, 具有自动化程度高, 生产线灵活的特点. 当接收到需要处理的命令时, 控制系统对AGV发送指令, AGV执行具体的指令, 完成物料货架的搬运工作, 等货架上的物品被取下后, 然后再将货架再送回至指定位置^[2].

本文通过对概率转换公式的改进和更新信息素, 提出一种改进的蚁群算法, 规划AGV的运行路线. 在规划最佳路径的同时, 需要考虑AGV互相之间的碰撞或与货架碰撞的情况. 通过时间窗模型, 为优化路径规划的模型和算法提供了有效的方法. 最后在基于理论的基础上, 结合仓储物流的实际运行环境, 建立栅格地图, 通过模拟仿真实验, 表明该算法可以快速、准确地获得最优解.

1 建立AGV的工作环境模型

在智慧仓储的制造车间内, 从AGV的起始移动位置到指定货物对应的货架位置, 需要获取一条优化的路径来引导AGV的运动^[3]. 首先根据AGV的工作环境建立模型, 通过模型的建立把车间内AGV的工作环境转化为机器能够识别的信息. 在制造车间内, 由于货物数量庞大, 货架布局时会尽量工整、对称, 为AGV的行驶设计出便于通行的过道. 因此在制造车间内, 只考虑静态障碍物的情况下, 所有障碍物的数量及规模都是有限的且已知的^[4].

1.1 栅格法

栅格法建立模型时将需要建模的空间环境视为一个平面, 然后将平面分割成一个个栅格, 存储了环境信息. 栅格类型可分为两种类型: 阴影部分表示障碍栅格(由1表示), AGV禁止通行的区域; 白色部分表示自由栅格(由0表示), AGV可以通行的区域^[5]. AGV只能在自由栅格中移动, 单位栅格的大小必须完全包含AGV^[6]. 为了避免碰撞, 在规定障碍物栅格时应该适当的预留出一定的安全空间. 本文使用栅格法^[7]将制造车间划分为由m×n个大小相同的栅格方块组成的二维空间.

路径规划的目标是寻找包含开始网格、结束网格和有序网格子集的网格集, 并在遇到障碍物网格时避开它们^[8]. AGV实时上报位置信息, 在这些栅格化的环境中, 将通过相应的算法检索路线, 遍历整个栅格地图并记录整个路线^[9]. 本文栅格环境的编号是从左到右、由下往上的, 如图1所示, 为模拟车间的10×10的栅格图模型.

按行驶方向, 图1中AGV1在节点32, 则它下一步到达的节点为33, AGV2在节点55, 则它下一步到达的节点为45.

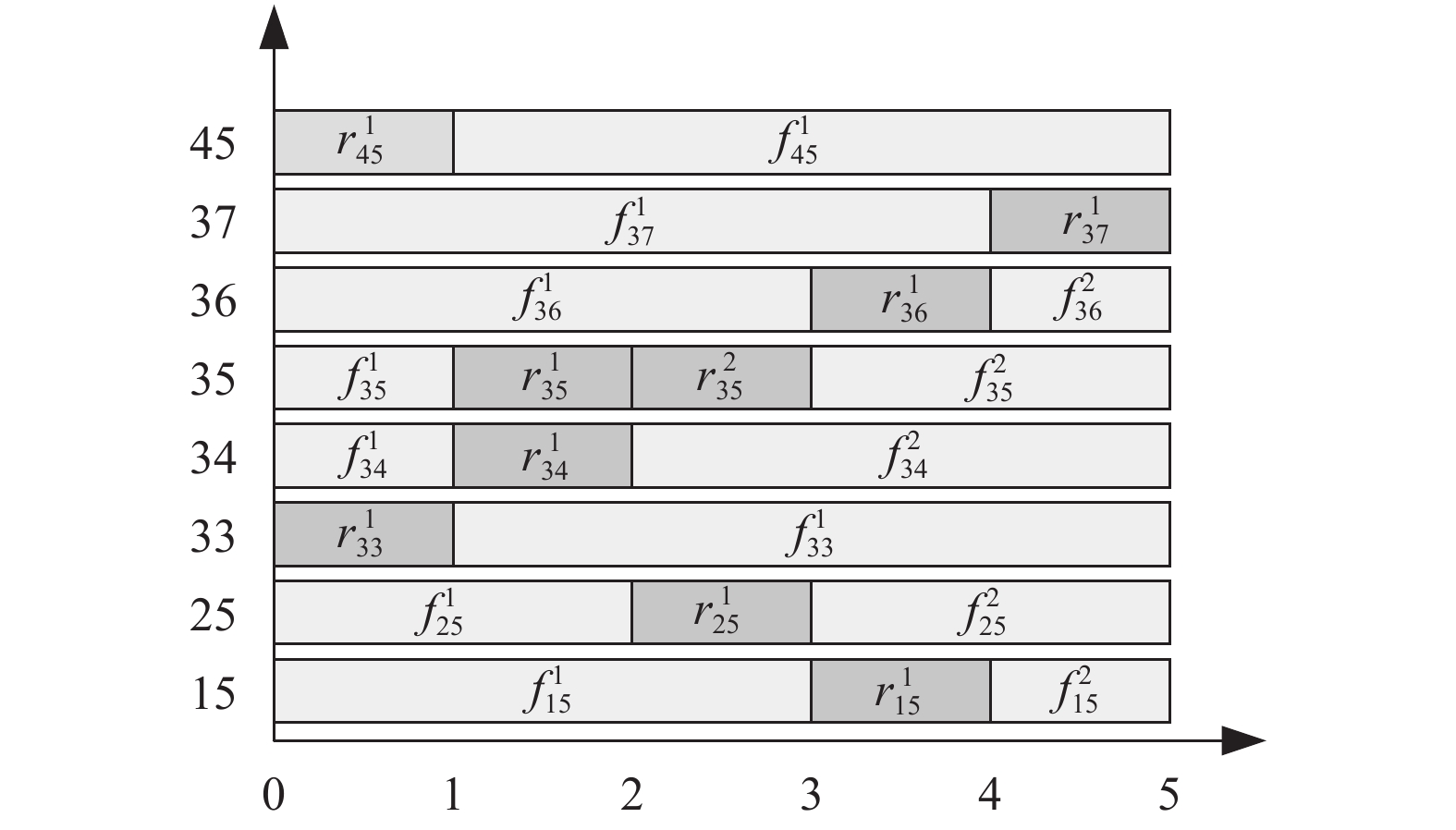
1.2 时间窗模型

AGV从进入节点到离开节点所形成的时间周期称为时间窗, 每个时间窗口的时间段只能通过当前AGV, 其他AGV不允许通过当前AGV停留时间窗内的节点^[10]. 在对多个AGV进行路径规划时, 为了避免出现冲突和死锁现象, 每个节点在任务开始到任务结束期内, 通过节点的AGV小车将时间划分为不同的预留时间段, 每个节点预留时间段中间的空闲时间间隔可以用来规划其他AGV的行驶路径, 此时其他AGV可以通过该节点.

AGV通过每个网格的时间可以通过各种传感器收集, 并且可以分为保留时间和空闲时间. 如图2引入变量: 保留时间 $r_n^k$ 是在第n个节点占用的第k个时间窗; 空闲时间 $f_n^k$ 是在第n个节点占用的第k个空闲时间窗^[11]. 通过空闲时间窗口来计划避障, 根据图1的两个AGV的行驶方向, 规划路径: AGV1的路径信息位节点32、33、34、35、36, 最终到达目标节点37, 相应节点的保留时间窗为 $r_{33}^1$ 、 $r_{34}^1$ 、 $r_{35}^1$ 、 $r_{36}^1$ 、 $r_{37}^1$ ; AGV2从起始节点55出发, 经过节点45、35、25, 到达目标节点15, 相应节点的保留时间窗为 $r_{45}^1$ 、 $r_{35}^2$ 、 $r_{25}^1$ 、 $r_{15}^1$ . 两个AGV的时间窗口模型的示意图如图2所示.

当出现选择路径冲突时, AGV行进的优先级先后顺序根据3个方面来制定: (1)装有行李架的AGV的优先级高于未装有行李架的; (2)任务完成设定的时间早的AGV优于任务完成时间迟的; (3)当出现两个AGV朝同一目标节点移动的情况, 后一个AGV根据等待策略重新规划^[12].

2 基于蚁群算法的路径规划

在智慧仓储物流中的路径调度规划需要解决3方面问题: (1) AGV与障碍物碰撞问题; (2)实现任务完成的时间最小化和货物运送效率最大化的目标; (3)传统的蚁群算法不能直接用于解决有障碍的最短路径问题. 因此, 应改进蚁群算法的实用性来解决障碍问题, 这也解决了理论上的困境问题.

2.1 基本蚁群算法

蚁群算法是以类比蚁群现实生活中寻找食物的行为为灵感. 蚂蚁在觅食的过程中随机行走, 并在沿途铺设名为信息素的化学痕迹. 信息网将信息发送给其他成员, 其他蚂蚁则很可能沿着铺有信息素的路径行走, 而不是随意走动. 这一观察结果启发了意大利学者Dorigo等人, 提出了一种智能多主体系统的启发式算法, 鲁棒性更强, 速度更快, 分布式计算和良好的可扩展性^[13], 并且具有实现全局最优解的概率更高.

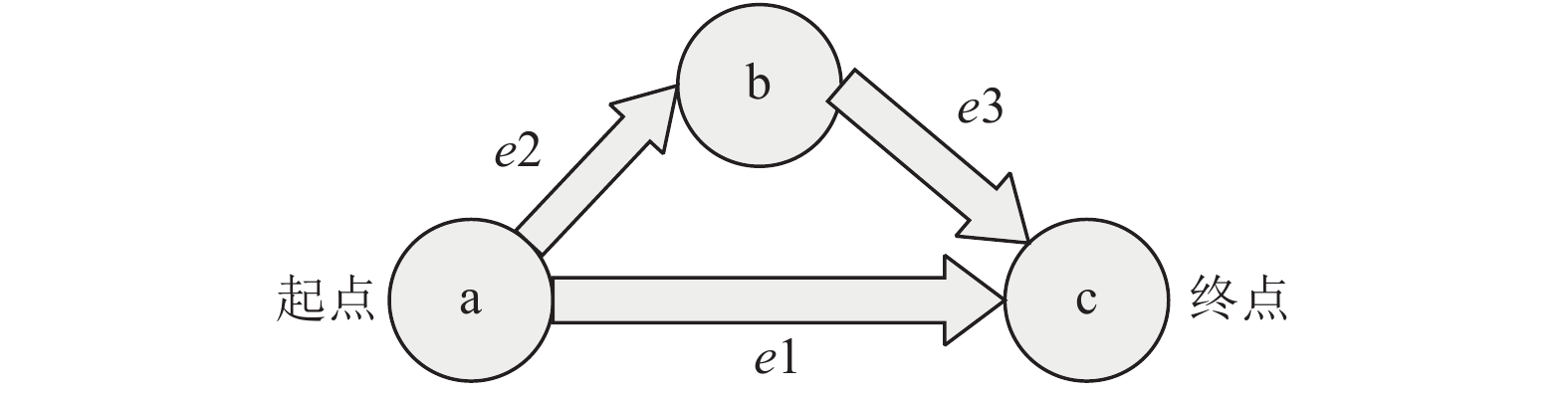
在蚁群算法中, 蚂蚁运动的过程可用图3表示. 蚁巢(起点)和食物(终点)之间往往有多条路径, 可用{e1}、{e2、e3}集合表示. 在蚂蚁觅食寻路的过程中, 信息素残留量会开始蒸发, 因此减少对蚂蚁的吸引力. 路径越长, 信息素蒸发量越多. 因此最短路径上的信息素强度增加到与蒸发速率相平衡的水平, 导致较短路径上的信息素数量比较长路径上的信息素增量更快. 在自动催化过程中通过信息素的积累, 当蚂蚁面对交叉点时, 信息素量越大的路径更易优先被选择.

完整的蚂蚁的寻路过程包括两部分: 路径选择和信息素释放.

$ {p}_{ij}^{k}\left(t\right) $ 表示在t时刻, 蚂蚁k位于栅格i时, 选择下一栅格j的概率, 表达式如式(1)所示:

$ {p}_{ij}^{k}(t)=\left\{\!\!\!\!\begin{array}{l}\frac{{[{\tau }_{ij}(t)]}^{\alpha }{[{n}_{ij}(t)]}^{\beta }}{{{\displaystyle\sum }_{j\in allo{w}_{k}}{[{\tau }_{ij}(t)]}^{\alpha }{[{n}_{ij}(t)]}^{\beta }}},j\in allo{w}_{k}\\ 0,{\text{其他}}\end{array}\right. $

(1)

其中, $ {allow}_{k} $ 表示蚂蚁k当前可以选择到达的节点的集合; $\alpha $ 表示信息启发因子, 用来表示蚂蚁在行路过程中积累的信息量产生的作用大小^[14], $\beta $ 表示期望启发因子, 值越大, 表示启发信息在蚂蚁运动方向的选择中越受重视^[15], $ {\tau }_{ij} $ 表示t周期时路段 $(i,j)$ 上的联系信息素, ${d_{ij}}$ 表示城市i与j之间的距离, ${\eta _{ij}}$ 表示启发函数, ${\eta _{ij}}$ 和 ${d_{ij}}$ 的关系如式(2)所示:

$ {\eta _{ij}} = \frac{1}{{{d_{ij}}}} $

(2)

蚂蚁在每次觅食中信息素的量主要由两个因素组成: 蒸发的信息素和新添加的信息素. 经过一段时间n后, 蚂蚁完成一个周期, 会更新并更改通过路径上的信息素数量, t+n时刻在路径(i,j)上信息素更新规则为:

$ {\tau _{ij}} = \left( {1 - \rho } \right) \cdot {\tau _{ij}}(t) + \Delta {\tau _{ij}}(t,t + n) $

(3)

$ \Delta {\tau _{ij}}(t,t + n) = \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k(t,t + n)} $

(4)

其中, $\rho $ 是信息素蒸发的速率, 且取值范围为 $\rho \in (0,1)$ , $1 - \rho $ 为信息素残差因子, $\Delta {\tau _{ij}}(t,t + n)$ 是在时间段 $(t,t + n)$ 内路径 $(i,j)$ 增加的信息素的量, 在循环开始时, $\Delta {\tau _{ij}}(0) = c$ . $\Delta \tau _{ij}^k(t,t + n)$ 是由蚂蚁k在 $(t,t + n)$ 增加的信息素的量.

2.2 改进蚁群算法

智慧物流制造车间的空间环境属于静态空间, 改进的蚁群算法通过环境地图和目标节点的位置信息, 通过优化概率转移公式来改变运动方向和信息素更新两个方面^[16], 选择从起始节点到目标节点的最佳路径. 在改进的算法中, 提高算法全局寻优能力和收敛性^[17].

2.2.1 优化概率转移规则

蚁群算法在禁忌表的限制下, 前期迭代的过程中会产生大量交叉路径, 导致蚂蚁行进的过程中容易进入一个凹形的障碍物区域, 出现无路可走的“死锁”状态时, 就成为路径死锁^[18]. 蚂蚁进入死角时, 死锁状态的位置如图4所示.

图4中, 蚂蚁运动到13节点时, 进入死角, 成为死锁状态. 在路径搜索过程中进入死角, 则死角的位置会被列在禁忌表中, 蚂蚁会返回到前一个位置, 然后搜索下一个位置. 本文通过建立死角表并引入惩罚函数^[19]来解决这个问题. 当蚂蚁遇到死角时, 使用惩罚函数而不是更新规则, 惩罚函数为:

$ \tau (i,j) = \lambda \cdot \tau (i,j),0 < \lambda < 1 $

(5)

惩罚函数使死角的周围边缘信息素减少, 指引蚂蚁在下一个迭代搜索的过程中忽略那些边缘, 解决了死锁问题, 加快找到运动方向路径.

2.2.2 信息素更新优化

S为起点, E为终点, n是从S到E(包括S和E)所经过的路径上的网格数^[20], m为转弯处网格数, AGV的速度保持恒定且转向模式是绕自己的中心旋转, 则用 ${v_s}$ 表示角速度. 网格的单位长度用 ${l_n}$ . 基本蚁群算法的路径成本函数为:

$ {L_{km}} = {L_{SE}} = n * {l_n} $

(6)

改进的路径成本函数为:

$ {L_{km}} = {t_{SE}} = \frac{{(n - 1) * {l_n}}}{{{v_s}}} + \frac{{m * \pi }}{{2 * {v_c}}} $

(7)

因此, $\Delta {\tau _{ij}}(t,\;t + n)$ 可以表示为:

$ \Delta {\tau }_{ij}^{k}(t,t+n)=\left\{\!\!\!\!\begin{array}{l}\dfrac{Q}{{L}_{k}},{\text{第}}{{k}}{\text{只蚂蚁经过}}({{i}},{{j}})\\ 0,{\text{其他}}\end{array}\right.$

(8)

Q表示信息素总量, 能在蚂蚁运动的过程中影响算法速度. ${L_k}$ 表示在此次任务中, 蚂蚁k所经过的路径长度.

2.2.3 算法步骤

本算法选用蚁群算法对智慧仓储物流的车间的地图模型进行优化, 设AGV的出发点为S, 目标货架为E处, 算法的目的目的是绕开所有障碍物, 寻找一条从S到E的最短路径, 引导AGV小车运作. 基于改进蚁群算法的路径规划的算法实现步骤如算法1.

算法1. 基于改进蚁群算法的路径规划算法

1) 初始化参数. 首先读取栅格地图的信息, 设置AGV个数m, 最大迭代次数K, 信息素强度Q以及 $\scriptstyle\alpha$ 、 $\;\scriptstyle\beta$ 、 $\;\scriptstyle\rho$ , 初始化常数 $\scriptstyle\Delta {\tau _{ij}}(0) = c$ . 将蚂蚁放在起始位置S处, 同时将此网格位置设置为禁忌表 $\scriptstyle tab{u_k}$ 的第一个元素, 此时各边上的信息素相等, 则 $\scriptstyle\Delta {\tau _{ij}}(0) = 0$ ;

2) 当蚂蚁k选择了下一个网格时, 如果不是目标网格, 则蚂蚁根据式(1)选择概率最高的下一个空闲网络; 如果是目标网格, 则该蚂蚁将在循环中完成了此次无碰撞路径的任务.

3) 根据式(4)和式(8)更新路由, 由式(7)计算在路线上消耗的最佳时间.

4) 重复执行2)、3), 直到蚂蚁到达终点或者无处可去, 迭代结束.

5) 根据式(3)更新信息素矩阵, 并且不考虑到达目的地的蚂蚁, 直到迭代结束.

通过改进的蚁群算法, 结合时间窗网格法, 多AGV的避障规划算法步骤如算法2.

算法2. 多AGV的避障规划算法

1) 根据优先级对所有AGV进行排序, 对优先级最高的AGV进行最优路径搜索, 得了该AGV所经过的所有网格都占据的时间窗, 然后初始化时间窗.

2) 安排下一个优先级高的任务, 并搜索下一个AGV的最佳路径, 同时获得该AGV通过的网格的时间窗口, 并更新所有网格的时间窗口. 将网格进行比较, 以确定是否发生时间窗口冲突.

3) 如果2) 中存在冲突, 则根据优先级规则采用等待策略, 将在 $\scriptstyle tab{u_k}$ 表(k = 1, 2, …, m)中放置冲突节点, 然后再次搜索路线. 如果2)中没有冲突, 则规划结束.

基于改进蚁群算法的多AGV的避障路径规划算法步骤流程图如图5所示.

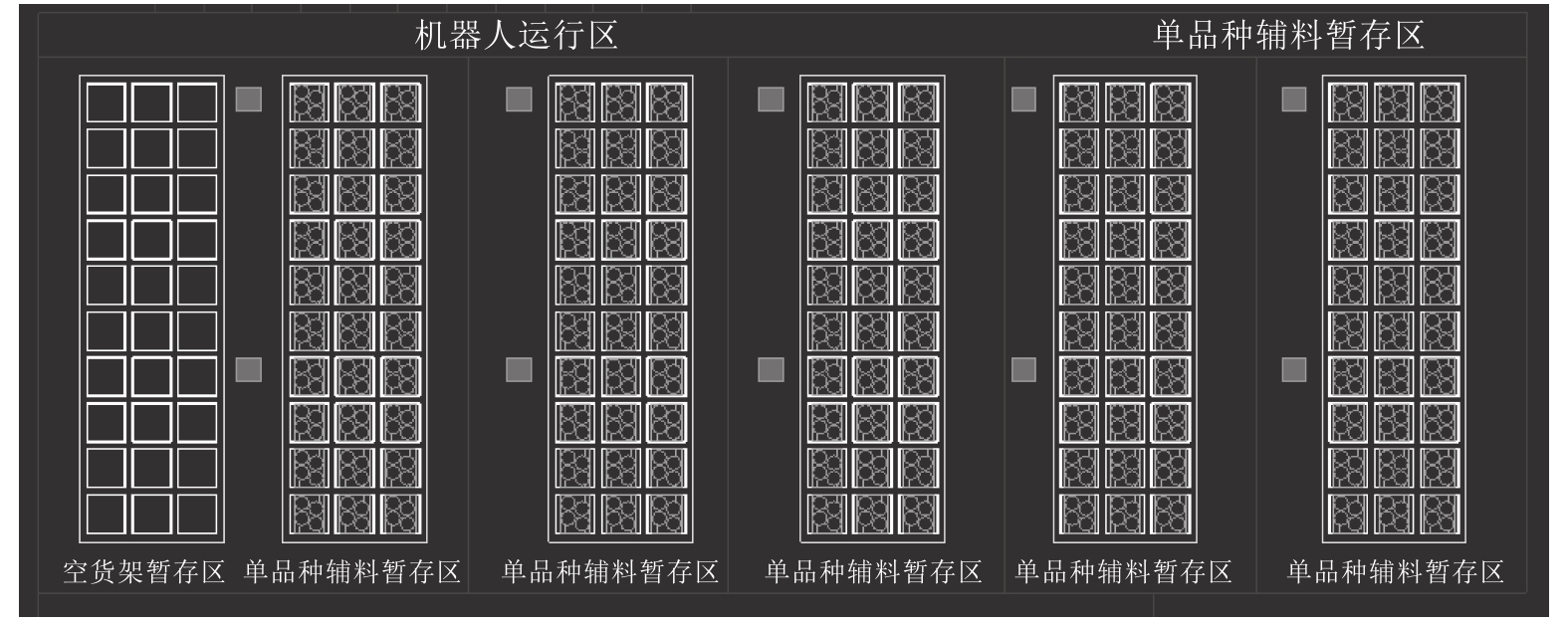
3 实验分析 3.1 路径优化仿真实验

已知某工厂生产车间的货物暂存区的平面设计图如图6所示.

本文通过Matlab仿真实验验证算法, 首先利用栅格法建立25×25仿真环境模型, 从左到右、从下到上对该环境进行编号, 蚂蚁数量m、信息启发因子 $\alpha $ 、期望启发式值 $\;\beta $ 、信息素的蒸发系数 $\; \rho $ 、信息素强度Q、最大迭代次数K的参数设置如表1所示.

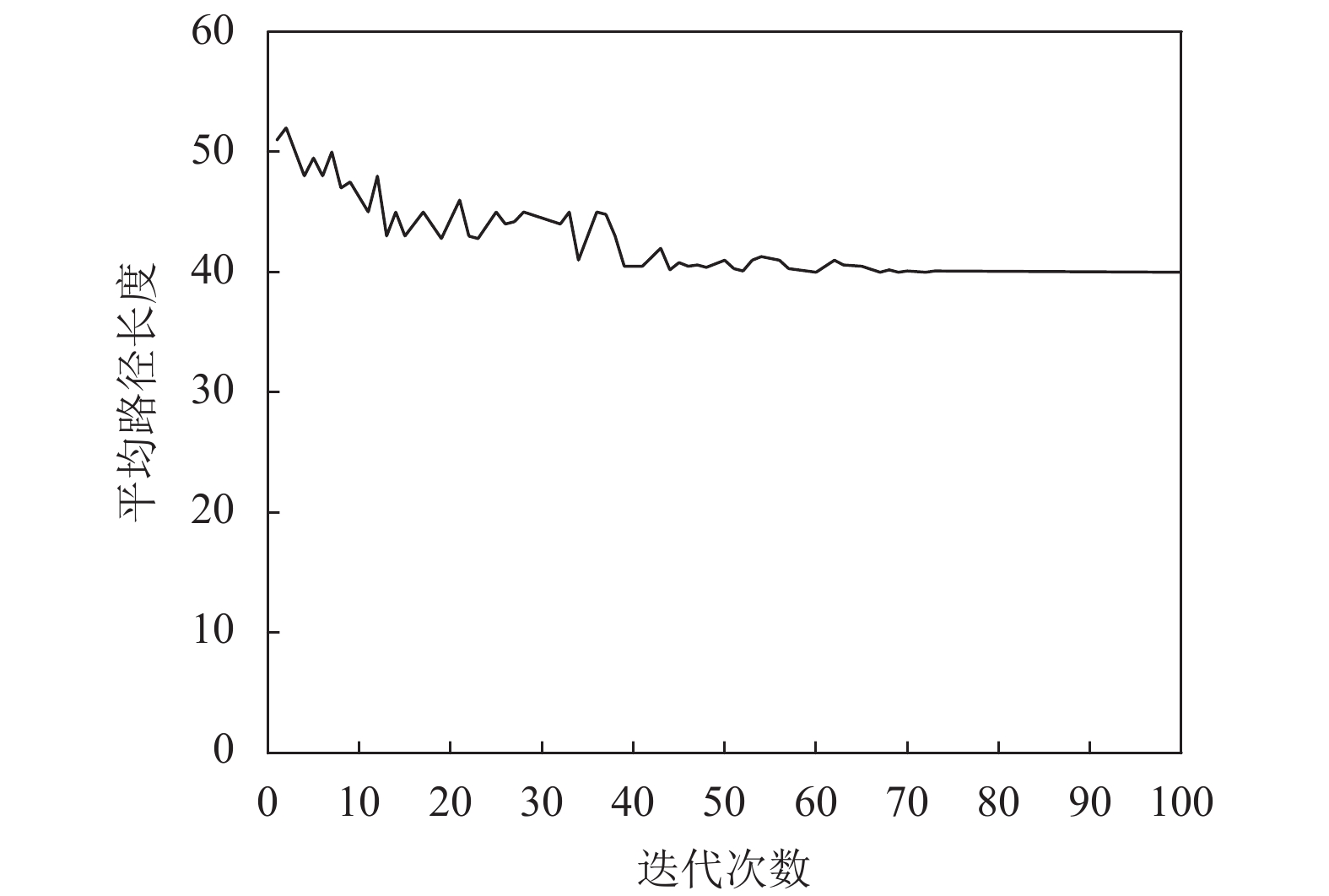
AGV车从起始节点25, 到达目标节点510. 仿真结果如图7、图8所示.

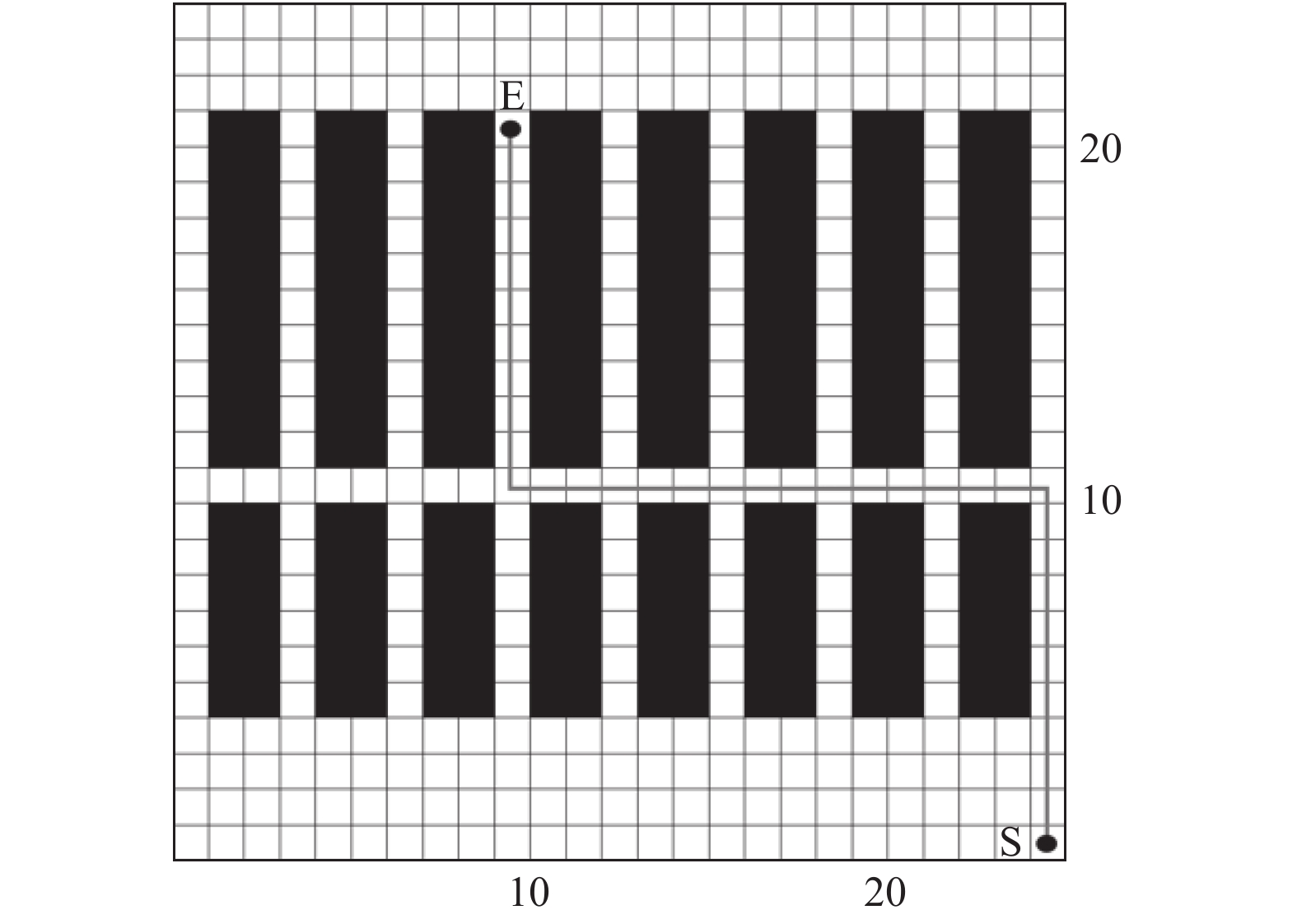
采用改进的蚁群算法对路径优化进行仿真, 仿真结果如图9.

根据实验结果结果表明, 由图8基本蚁群算法收敛曲线可得经过73次迭代后, 达到最短路径40, 而根据图10可得改进蚁群算法可以经过60次迭代后, 达到最优路径长度为38. 因此改进的蚁群算法具有更好的性能, 能加快收敛速度, 更快地找到最优路径.

3.2 多个AGV避障规划仿真实验

避障路径规划的仿真实验设计了3个AGV, 设置优先顺序为AGV1 >AGV2>AGV3, 各AGV的起始节点和目标节点位置参数如 表2所示.

根据算法2中步骤1)规划AGV1和AGV2的行驶路径, 分别从S1和S2出发, 冲突未解决时, 仿真结果如图11所示.

根据栅格地图和时间窗, 在节点94时存在冲突, 则AGV2将采用等待策略, 它将在节点上等待1 s, 以便AGV1能够提前通过冲突, 路径规划后的仿真结果如图12所示.

通过时间窗再次检测冲突, 由于没有冲突, 所以执行第二步, 根据AGV1和AGV2的路径规划, 更新所有节点的时间窗, 并搜索AGV3的最短路径. 当冲突未解决时, 仿真结果如图13所示.

根据时间窗模型, 当AGV3到达节点238之后, 与AGV1之间存在冲突, 因此再次搜索AGV3的最短路径, 并将节点238放置在AGV3的 $ {tabu}_{k} $ 表中, 最后进行路径规划. 仿真结果如图14所示.

通过对仿真结果的分析, 将改进的蚁群算法与时间窗模型相结合, 得到了较为理想的结果.

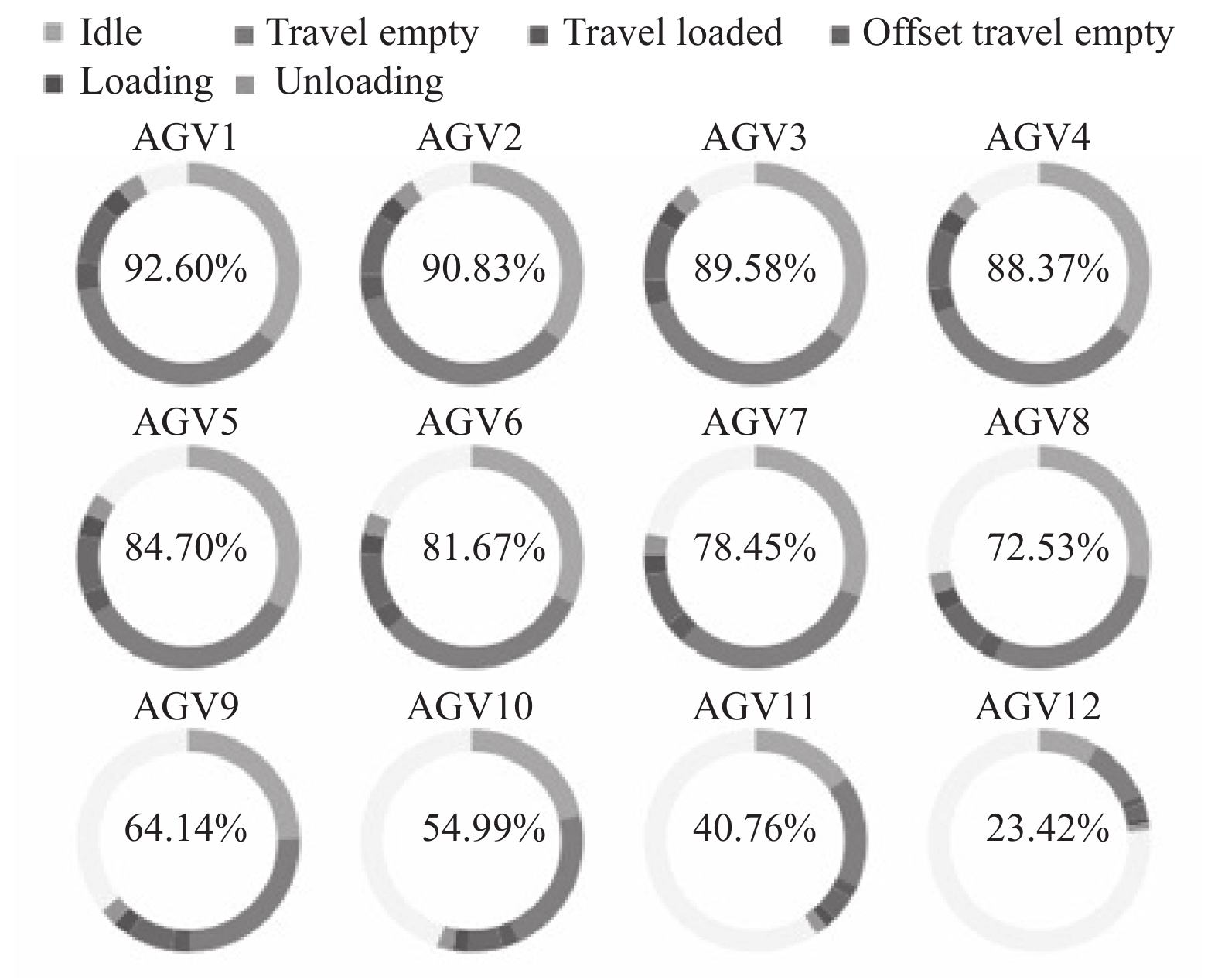
将本方法应用于某大型制造企业的生产物流系统设计中, 在Flexsim平台对该系统的入库环节进行物流仿真实验, AGV的数量为12, 各AGV的利用率如图15所示.

本方法应用于实际系统中, 在多AGV的路径规划中, 能够合理规划各AGV的行驶路线, 进而提高系统整体运输任务的效率, 保证系统顺利运行.

4 结论与展望

在智慧物流制造车间的环境下, 通过改进的蚁群算法结合带有时间窗的网格法根据环境的变化不断调整AGV的行驶轨迹. 本文以制造车间实际环境为模型, 建立仿真实验, 对单个AGV和多个AGV避障规划情况进行分析, 验证了该算法能有效避免在设备的碰撞问题. 本设计已经应用于某大型制造企业的生产物流的设计过程中, 不久将全面投入使用.

随着人工智能的迅猛发展, 发展智能制造, 智慧仓储物流已是整个制造业必然的发展趋势. 以智慧物流为核心的科学管理的、信息丰富的、决策智能的物流运营模式会成为人类社会不断追求的生产生活方式.