随着智能交通系统的发展, 交通预测越来越受到重视, 它是先进交通控制的重要组成部分. 准确地对交通进行预测对城市交通规划、交通管理和交通控制等方面起到了重要的作用. 交通预测是分析城市路网上的交通状况、包括流量、车速和密度等, 挖掘交通模式, 对路网上的交通进行预测的一个过程. 交通预测不仅能给管理者提供科学依据来预测交通拥挤并提前限制车辆出行提供科学依据, 而且还可以给城市出行者提供适当的出行路线, 提高出行效率提供保障. 然而, 交通预测由于其复杂的时空依赖性, 一直是一项具有挑战性的任务.
1 相关工作目前有很多交通预测的方法, 早期, 有一些是基于时间依赖性来进行分析的, 例如ARIMA模型[1]、卡尔曼滤波模型[2]和SVR[3]模型等. 但在实际应用中, 这些方法对于不稳定、非线性的数据处理是比较困难的.
近年以来, 随着深度学习的快速发展, 深度神经网络能够捕获交通数据的动态特征并取得很好的效果, 例如, 胡鑫泽等[4]构建了基于BP神经网络的模型来预测城市交通拥堵情况.
根据是否考虑空间依赖, 神经网络模型可以划分成两类. 一些方法只考虑时间依赖, 例如, 李校林等[5]构建了PF-LSTM来预测交通流量; 满春涛等[6]使用考虑上下游的LSTM网络来进行短时交通流量的预测, 这些模型考虑时间特征但忽略了空间依赖性, 所以交通数据的变化不受城市路网的限制, 因此不能精确的预测路上的交通状态.
解决交通预测问题的关键在于充分利用空间和时间依赖性, 为了更好地表现空间特征, 很多研究已经在这个基础上进行了改进. 例如, LYU等[7]提出了一个SAE模型从交通数据中捕获空间特征; 朱凯利等[8]使用图卷积神经网络来捕捉城市道路网络的空间特征, 实现短期交通流的预测; Yu等[9]使用深度卷积神经网络捕获空间依赖, 用LSTM捕获时间动态性, 在北京交通网络数据上展示出了SRCN模型优越性.
尽管上述方法引入了CNN来捕获空间依赖, 在交通预测任务上有很大的进步, 但CNN本质上只适用于欧氏空间, 在有着复杂拓扑结构的交通网络上具有局限性, 因此, 这类方法有缺陷. 近年以来, 随着图卷积神经网络的发展, 图卷积神经网络(GCN)能够被有效提取网格数据的的空间特征, 为上述问题提供更好的解决方案.
在这一背景下, 本文提出了一种新的深度学习模型: 基于注意力机制的时空图卷积网络, 可以从交通数据中捕获复杂的时空特征, 将其用于基于城市路网的交通预测任务上. 与其他模型相比, A-TGCN不仅可以捕捉空间形态和时间动力学的判别特征, 而且可以探索时空域之间的共生关系.
2 问题描述与建模 2.1 问题描述和定义在本文中, 交通预测的目标是基于道路上的历史交通信息来预测未来某段时间内的交通信息. 本文将交通速度作为实验中的一个预测对象.
定义1. 路网
定义2. 特征矩阵
可以将时空交通预测的问题视为在确定了道路网络拓扑结构
| $ \left[ {{X_{t + 1}}, \cdots {X_{t + T}}} \right] = f\left( {G;\left( {{X_{t - n}}, \cdots ,{X_{t - 1}},{X_t}} \right)} \right) $ | (1) |
其中,
获取复杂的空间依赖在交通预测中是一个关键性问题. 传统的CNN只能应用于欧氏空间, 比如说图片, 常规网格等. 但是城市路网并不是网格, CNN不能反映其中复杂的拓扑结构. 近年来被提出的GCN可以处理图结构, GCN的原理是在傅里叶域中构建滤波器, 作用在顶点及其一阶邻居上, 捕获顶点间的空间特征, 可以通过堆叠多个卷积层来构建 GCN 模型. GCN模型可以获取中心道路及其周围道路的拓扑关系, 以获取空间依赖. 总之, 本文使用 GCN模型[10]从交通数据中提取空间特征. 对于本文, GCN模型可以表示为:
| $ f\left( X \right) = \sigma \left( {\widehat AX{W_0}} \right) $ | (2) |
式中, X表示特征矩阵, A表示邻接矩阵,
获取时间依赖是交通预测中的另一个关键问题. 目前, 用于处理序列数据被最广泛使用的是递归神经网络(RNN). 但是, 由于梯度消失和梯度爆炸等缺陷, 传统的递归神经网络对长期预测具有局限性.
LSTM模型是RNN模型的变体, 并且已被证明可以解决上述问题. LSTM的基本原理是使用门控机制来记忆尽可能多的长期信息, 因此选用LSTM模型为基础进行改进, 从交通数据中获取时间依赖.
基本LSTM模型如图1所示.

|
图 1 LSTM模型 |
图1中
经过改进后的LSTM模型如图2所示.
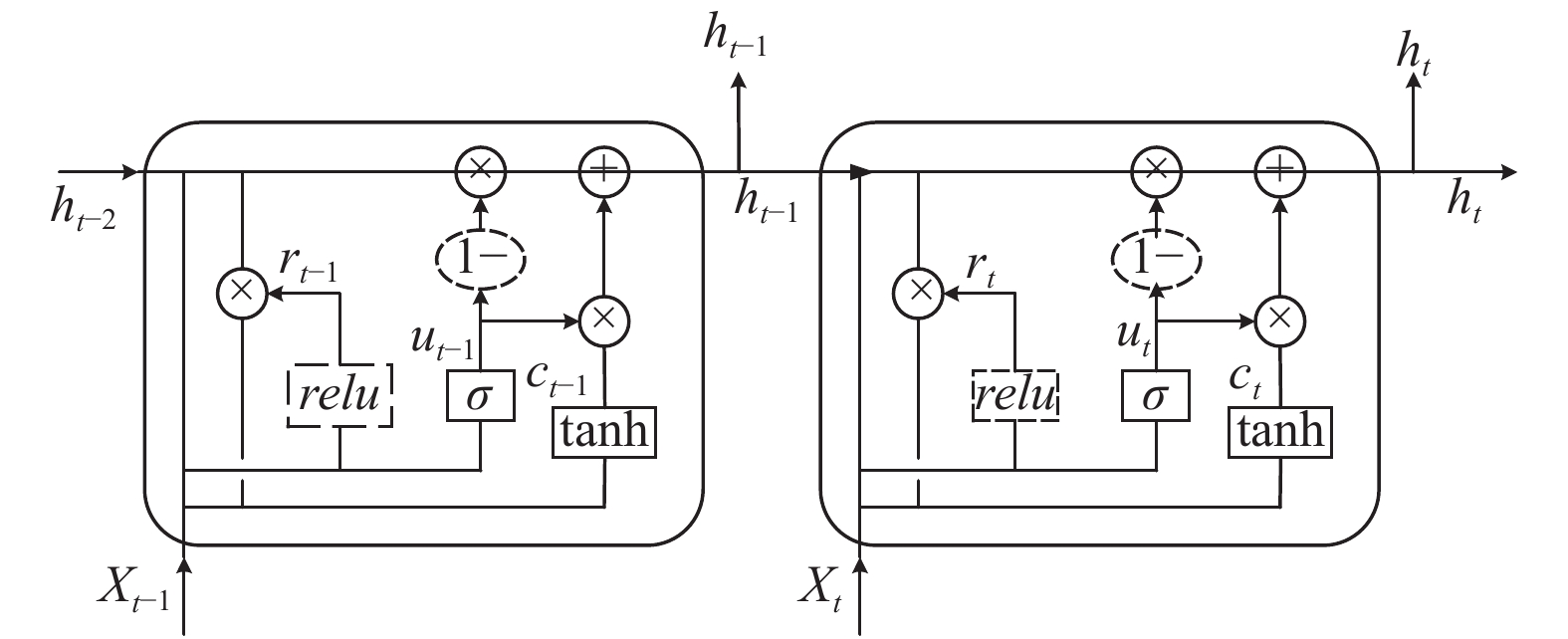
|
图 2 改进的LSTM模型 |
将
| $ {r}_{t}=relu\left({W}_{r}·\left[{h}_{t-1}+{X}_{t}\right]\right) $ | (3) |
| $ {u}_{t}=\sigma \left({W}_{u}·\left[{h}_{t-1}+{X}_{t}\right]\right) $ | (4) |
| $ {c}_{t}=\mathrm{tanh}\left({W}_{c}·\left[{r}_{t}\ast {h}_{t-1}+{x}_{t}\right]\right) $ | (5) |
| $ {h_t} = \left( {1 - {u_t}} \right) * {h_{t - 1}} + {u_t} * {c_t} $ | (6) |
式中,
改进后的LSTM模型拥有更少的输入和输出以及门控逻辑单元, 能够拥有更好的时间复杂度. 并且调整了激活函数, 实验结果表明其能够更好地挖掘图拓扑结构的数据.
2.4 A-TGCN模型为了从交通数据中同时捕获时间和空间依赖性, 我们提出了一种基于图卷积神经网络和改进的LSTM模型的基于注意力机制的时间图卷积模型(A-TGCN).
A-TCN模型有3个部分: 图卷积网络, 改进的LSTM以及注意力机制. 一方面利用图卷积网络来捕捉城市道路网的拓扑结构, 从而得到空间相关性. 另一方面, 利用门控逻辑单元捕捉道路上交通信息的动态变化, 获取时间相关性. 本文的模型使用图卷积网络算子来替换循环神经网络中的门控逻辑单元, 与Ling等人[11]所提出的T-GCN相比, 该模型在捕捉空间特征的同时将其融合进入时间特征中, 使得空间特征在随着时间序列的推进过程中产生关联性. 相比于先进行空间特征捕捉, 再进行时间特征捕捉的模型, 该模型减弱了由于传递过程中所造成的信息丢失所产生的误差逐渐放大的现象, 并且在每个A-TGCN模块中加入了注意力机制, 使得该模型在每个时间段能够对路网上节点的信息进行动态的聚焦, 从而提升了模型的泛化能力, 也让该模型在进行长时间交通信息预测是拥有更好的性能.
模型的结构如图3所示, 其中

|
图 3 A-TGCN模型的结构 |
图3中的LS-GCN细胞就是通过结合GCN, 改进的LSTM以及注意力机制相融合, 提出的新的网络模型. A-TGCN和改进的LSTM一样包含3个门: 重置门
图4中
| $ {r_t} = relu\left( {{W_r}\left[ {f({X_t}) + f({H_{t - 1}})} \right] + {b_r}} \right) $ | (7) |
| $ {u_t} = \sigma \left( {{W_u}\left[ {f({X_t}) + f({H_{t - 1}})} \right] + {b_u}} \right) $ | (8) |
| $ {u_t} = \sigma \left( {{W_u}\left[ {f({X_t}) + f({H_{t - 1}})} \right] + {b_u}} \right) $ | (9) |
| $ {c_t} = \tanh \left( {{W_c}\left[ {{r_t} * f({H_{t - 1}}) + f({X_t})} \right] + {b_c}} \right) $ | (10) |
| $ {h_t} = \left( {1 - {u_t}} \right) * {H_{t - 1}} + {u_t} * {c_t} $ | (11) |
| $ {H_t} = {f_{\rm {att}}}({h_t}) + {h_t} $ | (12) |
式中,

|
图 4 A-TGCN细胞的具体结构 |
2.5 注意力网络
通过GCN和门控逻辑单元模块所获取到的为包含空间特征的时间序列信息. 这就意味着, 在时间序列中, 路网中的信息一直在动态的变化, 所以在不同的时间点对于路网中各个节点的关注权重是不同的. 但是, 在每个时刻, 应该全局性的关注路网上的每个节点, 而不是单独的几个节点, 因此, 本文通过使用Soft-attention[12]机制, 它能够对于输入的序列提取的特征信息, 寻找其内部联系, 从不同时间点的路网信息中自适应的衡量各个节点的重要程度.
本文使用的注意力网络的结构如图5所示. 首先, 将t时刻所以节点的信息聚合为一个向量. 这里的信息包含t时刻路网的空间特征和节点信息.
图5中
| $ {q_t} = {{re}} lu\left( {\sum\limits_{i = 1}^N {W{h_{ti}}} } \right) $ | (13) |
式中,
那么所有节点的注意力分数的计算方法如式(13)所示:
| $ {\alpha _t} = Sigmoid\left( {{U_s}\tanh \left( {{W_h}{h_t} + {W_q}{q_t} + {b_s}} \right) + {b_u}} \right) $ | (14) |
其中,
该注意力机制将t时刻所有节点聚合后的信息与t时刻所有节点的信息进行拼接, 再通过全连接层, 从而得到各个节点相对于全部节点的的注意力权重. 因为解决的是非线性关系, 所以本文采用了两层全连接层的结构. 可能存在多个关键节点, 本文使用
因此

|
图 5 注意力机制结构图 |
2.6 损失函数
在训练过程中, 目标是使道路上的实际交通速度与预测值之前的误差最小. 本文使用
| $ loss = \left\| {{Y_t} - {{\hat Y}_t}} \right\| + \lambda {L_{\rm {reg}}} $ | (15) |
式中, 第一项用来最小化实际车速和预测值之间的误差, 第二项
为了检验A-TGCN模型的性能, 构建交通流预测系统并选取城市道路历史平均速度进行测试, 将A-TGCN模型和其他经典模型的预测结果进行比较, 来分析模型的优劣.
3.1 实验数据的选取实验选取了两个真实世界数据集SZ-taxi数据集和Los-loop数据集来评估A-TGCN模型的预测性能.
SZ-taxi: 该数据集为深圳市2015年1月1日至2015年1月31日的出租车轨迹. 选择罗湖区156个主要道路为研究区. 实验数据包括两部分: 一个是156×156邻接矩阵, 描述了道路之间的空间关系. 每行代表一条道路, 矩阵中的值代表道路之间的连通性. 另一个是特征矩阵, 它描述了每条道路上的速度随时间的变化. 每行代表一条道路; 每列是不同时段道路上的交通速度. 每15分钟汇总一条道路的交通速度. 从中选取一条道路上的速度如图6所示.

|
图 6 深圳数据中一条道路的速度随时间变化图 |
(2) Los-loop: 该数据集是在洛杉矶市的高速公路上实时收集的数据. 从2012年3月1日到2012年3月7日, 每5分钟汇总一次交通流量. 和SZ-taxi数据集类似, 数据分为邻接矩阵和特征矩阵两部分. 从中选取一条道路上的速度如图7所示.

|
图 7 Los-loop数据中一条道路的速度随时间变化图 |
在实验中, 将数据预处理, 输入数据被标准化在[0, 1]之间. 其中, 80%的数据用作训练集, 20%的数据用作测试集. 将预测接下来的15分钟、30分钟、45分钟和60分钟的交通速度.
3.2 性能评估指标为了评估A-TGCN的预测性能, 使用2个指标来评估实际交通情况
(1) RMSE:
| $ RMSE = \sqrt {\frac{1}{n}{{\sum\nolimits_{i = 0}^n {\left( {{Y_t} - \hat {{Y_t}}} \right)} }^2}} $ | (16) |
(2) Accuracy:
| $ Accuracy = 1 - \frac{{{{\left\| {Y - \hat Y} \right\|}_F}}}{{{{\left\| Y \right\|}_F}}} $ | (17) |
其中,
A-TGCN模型的参数主要包括: 学习率, 训练次数以及隐藏层数. 在实验中, 将学习率设置为0.001, 将训练次数设定为1000次.
隐藏单元的数量对于A-TGCN模型是非常重要的参数, 不同的隐藏单元会影响预测精度. 为了选择最佳值, 尝试使用不同的隐藏单位, 通过模型
在实验中, 对于SZ-taxi数据集, 使用二分法来寻找最优的隐藏单元的数量, 并分析预测精度的变化. 如图8所示, 横轴表示隐藏单元的数量, 纵轴表示
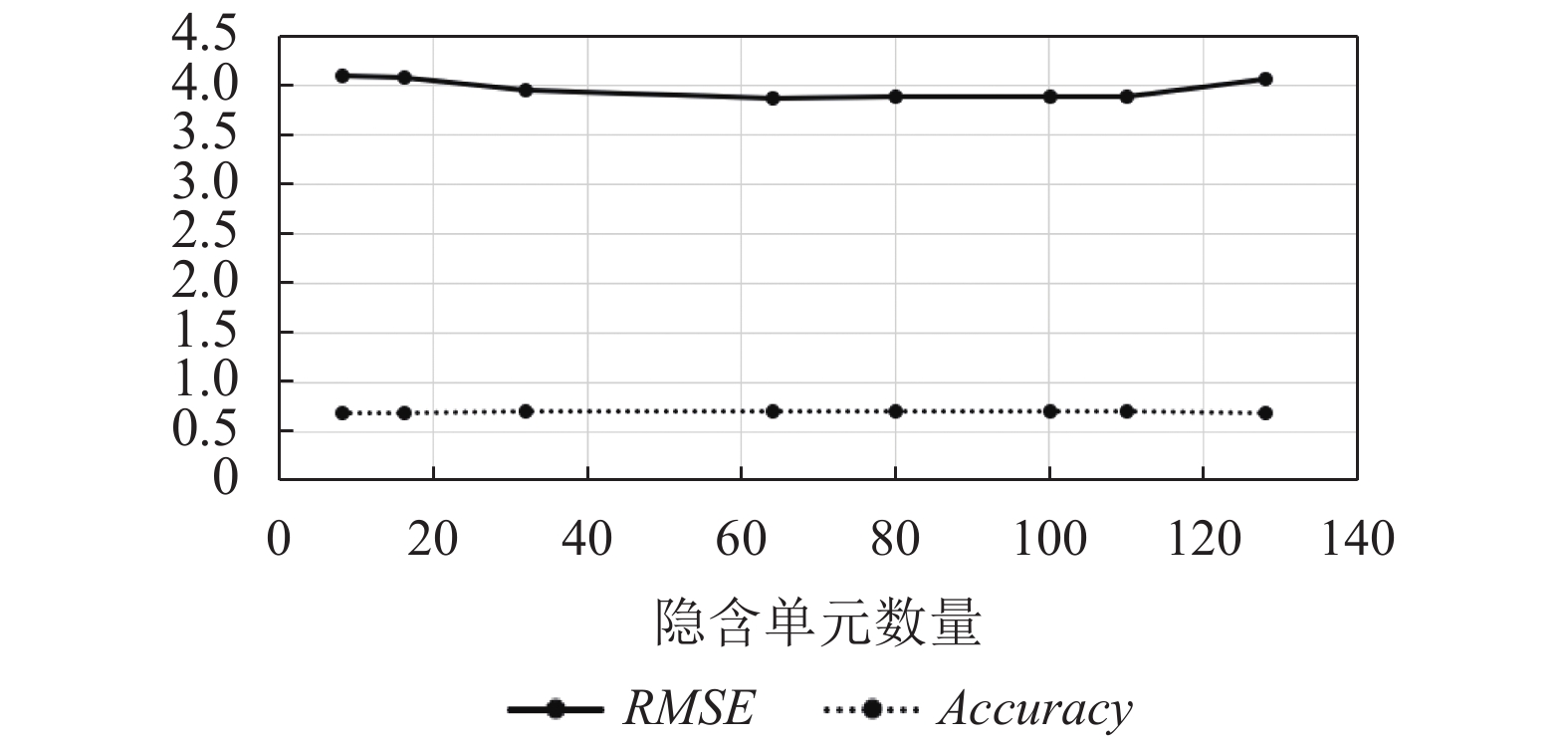
|
图 8 SZ-taxi数据不同隐含单元数量对应的模型效果比较 |
对于Los-loop的数据也使用相同的方法. 经过实验发现, 当隐藏单元数为16时, 预测精度最高, 而预测误差最低. 所以最终将Los-loop数据隐藏单元数量设置为16.
4 实验结果与分析本文将A-TGCN模型的性能与以下模型进行比较:
(1) SVR: 该模型通过使用历史数据来训练模型, 并获得输入和输出之间的关系, 来对未来交通数据来进行预测.
(2) ARIMA: 将时间序列拟合到参数模型中来预测未来的交通数据.
(3) LSTM+GCN: 单纯使用长短期网络和图卷积神经网络, 捕获时间和空间特征进行预测.
(4) T-GCN: 使用GCN和GRU, 先使用GCN捕捉空间信息, 再送入使用GRU捕捉空间信息.
表1和表2显示了在SZ-taxi和Los-loop数据集上分别进行15分钟, 30分钟, 45分钟和60分钟预测的A-TGCN模型和其他模型上的结果. 可以看出, A-TGCN模型在评估范围内均获得了良好的预测性能, 证明了A-TGCN模型在时空交通量预测中的有效性.
| 表 1 A-TGCN模型和其他方法在SZ-taxi数据集上的预测结果 |
| 表 2 A-TGCN模型和其他方法在Los-loop数据集上的预测结果 |
(1) 预测精度: 基于神经网络的模型, 包括T-GCN模型, A-TGCN模型等方法, 一般都比SVR, ARIMA等传统机器学习算法具有更好的预测精度. 例如, 对于深圳数据15 min的交通量预测任务, A-TGCN模型的RMSE误差比SVR模型降低了约10%, 准确率比SVR模型提高了约24%. 这主要是由于SVR模型和ARIMA模型难以处理复杂, 非平稳的时间序列数据, 因为ARIMA是通过计算各节点误差并求平均值来计算的, 如果时间的波动较大, 也将增加最终预测的总误差. GCN模型预测效果差的原因是因为GCN只考虑了空间特征, 忽略了交通数据的时间特征.
(2) 在Los-loop数据上的实验结果比在SZ-taxi数据上的要好. 经过推测, 主要原因是GCN模型在傅立叶域中定义了一个平滑的滤波器, 并通过不断移动滤波器来捕获空间特征, 所以在处理更加平滑的数据时, 会具有更好的效果. 从图6和图7, 以及GCN模型分别在两个数据上的预测结果, 可以看出, Los-loop数据更加的平滑, 总体的预测结果也越好.
(3) LSTM-GCN模型相比于T-GCN模型和A-TCN模型在进行长时间的预测时的能力下降的更快. 本文分析, 主要是因为LSTM-GCN模型没有对时间和空间特征进行联合的特征挖掘, 而是分步进行, 这就导致了在较长的时间序列的数据的传递过程中不可避免地出现信息的丢失, 时间越长, 丢失的信息就越多, 最终的预测结果造成较大的误差.
(4) T-GCN相比于A-TGCN模型在长时间序列的预测方面的能力也有所下降, 特别是对未来60分钟的交通流进行预测时, TGCN模型的准确率衰减的较为厉害. 本文认为, 首先, 相比于T-GCN只是将GCN模型挖掘出的空间特征在GRU中联合计算, A-TGCN模型是将GCN模型集成于循环神经网络中, 使得空间特征随着时间序列的推移实现了不同时刻的空间特征的动态关联性, 增强了信息传递的时空依赖性, 其次, A-TGCN模型在每个A-TGCN细胞中加入了注意力机制, 使得神经网络能够具备专注于输出信息中的重要特征的能力, 从而使得重要的特征能够一直传递下去.
5 结论与展望本文提出了一种新的基于神经网络以及注意力机制相结合的交通预测方法, 称为A-TGCN. 一方面, GCN用于捕获路网的拓扑结构以获取空间依赖性; 另一方面, 改进的LSTM模型用于捕获节点属性的时间动态变化以获得时间依赖性. 最终, 使用Soft-attention机制来自适应聚焦于关键节点, 增强预测效果.
在两个真实的交通数据集上进行评估, 在与ARIMA模型、SVR模型、GCN模型, LSTM+GCN以及T-GCN模型进行比较后, A-TGCN模型无论在长期还是短期的交通速度预测能力都优于这几种算法, 也更加接近真实的数据. 总之, A-TGCN模型可以成功地从交通数据中捕获时空特征, 并且不仅局限于交通速度预测, 还可以应用于其他的时空序列预测的任务.
| [1] |
刘学刚, 张腾飞, 韩印. 基于ARIMA模型的短时交通流预测研究. 物流科技, 2019(12): 91-94, 102. DOI:10.13714/j.cnki.1002-3100.2019.12.024 |
| [2] |
范光鹏, 孙仁诚, 邵峰晶. 基于LSTM和Kalman滤波的公交车到站时间预测. 计算机应用与软件, 2018, 35(4): 91-96. DOI:10.3969/j.issn.1000-386x.2018.04.017 |
| [3] |
潘伟靖, 陈德旺. 基于GRU-SVR的短时交通流量预测研究. 计算机技术与发展, 2019, 29(10): 11-14. DOI:10.3969/j.issn.1673-629X.2019.10.003 |
| [4] |
胡鑫泽, 张琪虹, 孙涵莆, 等. 基于BP神经网络的城市交通拥堵情况预测. 电子技术与软件工程, 2020(1): 186-187. |
| [5] |
李校林, 吴腾. 基于PF-LSTM网络的高效网络流量预测方法. 计算机应用研究, 2019, 36(12): 3833-3836. DOI:10.19734/j.issn.1001-3695.2018.06.0394 |
| [6] |
满春涛, 康丹青. 考虑上下游的LSTM短时交通流量预测. 哈尔滨理工大学学报, 2019, 24(5): 101-107. DOI:10.15938/j.jhust.2019.05.017 |
| [7] |
Lv YS, Duan YJ, Kang WW, et al. Traffic flow prediction with big data: A deep learning approach. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 865-873. |
| [8] |
朱凯利, 朱海龙, 刘靖宇, 等. 基于图卷积神经网络的交通流量预测. 智能计算机与应用, 2019, 9(6): 168-170, 177. DOI:10.3969/j.issn.2095-2163.2019.06.035 |
| [9] |
Yu HY, Wu ZH, Wang SQ, et al. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors, 2017, 17(7): 1501. DOI:10.3390/s17071501 |
| [10] |
Bruna J, Zaremba W, Szlam A, et al. Spectral networks and locally connected networks on graphs. Proceedings of the 2nd International Conference on Learning Representations. Banff, AB, Canada. 2014.
|
| [11] |
Zhao L, Song YJ, Zhang C, et al. T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(9): 3848-3858. DOI:10.1109/TITS.2019.2935152 |
| [12] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. arXiv: 1706.03762, 2017.
|
 2021, Vol. 30
2021, Vol. 30



