雷达是现代防空探测预警系统的重要设备, 结构复杂, 使用频率高, 从而导致故障率高. 为保障作战任务的顺利完成, 及时了解雷达装备的健康状态具有非常重要的意义. 特别是雷达发射机是雷达的核心功能部件, 具有高功率、大电流、高电压及热耗大等工作特点, 可靠性最低, 保障难度大. 因此选择雷达发射机作为健康状态研究对象, 具有典型的指导意义和实用价值[1].
健康状态的评估主要有两种, 一种是评估设备的健康状态等级. 比如按照国军标的要求, 雷达可分为健康、亚健康、注意、恶化、病态等5个等级[2], 也有根据实际情况分为健康、注意、警告、故障等4种状态的. 另一种则是对健康状态的量化, 分析设备的健康度, 可以更加准确的反映设备的健康程度, 避免了分级的不统一性和粗放型. 目前大部分健康状态评估研究是评估设备的健康状态等级, 其本质是利用采集参数进行数据融合, 确定设备的健康等级类别[3]. 鉴于设备健康状态的模糊性, 采用模糊综合评判方法进行健康状态评估是一种广泛使用的方法[4-6]. 随着大数据分析技术的成熟, 利用机器学习进行健康状态评估的研究也不断涌现[7,8].
设备健康度一般用0到100的范围来说明设备的健康程度. 其中0表示故障状态, 100表示非常健康的状态. 为了更加准确地判断设备的健康程度, 目前对设备健康度的研究日益增多. 文献[9]把设备的健康状态看做一个灰色系统, 构建一个虚拟健康向量, 用灰色关联法计算采集向量和虚拟向量的关联度得到健康度. 文献[10]分析不同属性的相关性关系, 通过信息熵方法进行量化来实时监控生产线健康度. 也有基于机器学习方法来进行健康度的评价的研究[11,12], 但是考虑到大多数设备缺乏足够的数据进行训练, 这方面的研究并不多. 更多的研究是把采集参数看做一组向量, 利用采集向量和不同健康等级的向量相关性来评价健康度, 使用较多的算法有马氏距离、余弦相似度、高斯相似度等[13-15]. 鉴于各个参数在健康度中的影响不同, 文献[16,17]提出了综合权重的健康度分析方法. 为了防止单个参数异常可能信息被淹没的现象, 文献[18]提出了动态权重机制, 文献[19]提出了利用变权权重替换常权权重, 以得到科学的健康度指标. 相较于传统的权重指标大多通过专家经验或者统计概率来获取, 文献[20]利用大数据分析权重提供了一种新思路, 但需要大量数据进行分析.
目前, 针对设备健康度的分析方法还不够成熟. 主要问题是没有考虑个别或者少数参数恶化对整个设备健康度的影响程度. 鉴于此, 本文利用向量相似性原理, 重点关注少量指标恶化对整个设备健康度的影响效果, 提出了一种新的动态权重指标模型. 其主要思想是考虑采集参数的类别和大小变化对健康度的影响不同, 构建基于指数函数的动态权重模型. 通过对模型中有关参数的设置, 可以得到比较准确的健康度数据, 为实现设备精细化健康管理奠定基础.
1 动态权重的健康度计算方法 1.1 动态权重机制某型雷达发射机目前采集了二十多个与健康状态相关的参数. 根据其结构特点, 有些部件是关键件, 一旦状况不佳将影响整个发射机的运行; 有些是非关键零部件, 出现故障可能会让发射机工作状况不佳, 但不至于影响整体运行; 还有些具有备份, 是并联部件, 即使损坏也不影响设备的正常工作, 但是显然会降低设备的健康度. 综合这些情况说明, 不同采集参数类别对雷达健康度的影响程度是不一样的.
为了更好地描述不同参数对健康度的影响, 参考相关文献的做法, 将权重分为静态权重和动态权重两种类型. 其中, 静态权重说明了各个参数对健康度的固定贡献, 一般根据经验值或者某种机制来决定, 比如该参数的变化程度(方差)、某个时间内该参数超界发生故障的次数等. 在本方法中, 静态权重一开始通过专家打分确定, 然后在运行过程中, 自动不断修正, 以反映雷达运行的实际情况. 静态权重的大小由静态权重指数决定. 静态权重指数计算公式如下:
| ${w_{{{is}}}} = {w_{{{i0}}}} + \alpha \cdot{\delta _{{i}}} + \beta \cdot{\gamma _{{i}}}$ | (1) |
在式(1)中, 对于参数i, 其权重指数wis由3部分构成. wi0是专家打分的结果. δi是参数的归一化方差值. 采用归一化处理是为了消除量纲的影响. α是方差修正参数. γi是最近一年该参数出现故障的次数, β是故障次数修正参数.
根据设备实际运行中总结的经验得知, 不同参数在取值不同时对设备健康程度影响有很大差别. 当参数值在健康区域周围时, 参数静态权重起主要作用. 但是当采样参数值偏离正常区域越大, 越接近报警区间, 其对设备健康状态的影响也越大. 用动态权重指数表示某个采样参数对健康状态的影响程度, 则其规律可用图1来表示.

|
图 1 状态数据与健康状态影响权重指数关系 |
在图1中, 横轴表示采集参数值, x0表示最佳值, xmin和xmax分别表示最小最大报警区间. 纵轴表示健康状态影响程度的权重指数, 在采集参数值处于最佳值附近时, 其体现的权重指数处于最低值w0, 实际上体现了静态权重指数. 参数值向下偏离或者向上偏离最佳值, 都会对导致健康状态的恶化程度增加, 体现在相应的动态权重指数增加. 通常向不同方向偏离的影响程度可能不同, 但根据总结, 其增加趋势皆呈现一定的指数形式增长. 因此动态权重使用指数函数进行建模, 表示如下:
| ${{{w}}_{{{id}}}} = {{a}}_{{i}}^{{{x}}{{_{{i}}^{{'}}}_{}}}$ | (2) |
其中, ai
是采集参数i动态权重的指数函数底数值, 且ai>1. 按照参数i在报警区域对整个设备的健康状态影响而定. 影响越大, ai的值越大. 不同采集参数具有不同的ai值. 为了消除采样数据量纲的影响, 并且更方便地确定ai值, 可让
| $ x_i^{'} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{x_i^{} - {x_{i0}}}}{{{{max }_i} - {x_{i0}}}}},&{{\text{当}}x_i^{} > {x_{i0}}{\text{时}}}\\ 0,&{{\text{当}}x_i^{} = {x_{i0}}{\text{时}}}\\ {\dfrac{{x_{i0}^{} - {x_i}}}{{{x_{i0}} - {{min }_i}}}},&{{\text{当}}x_i^{} < {x_{i0}}{\text{时}}} \end{array}} \right. $ | (3) |
其中, xi是参数i的监测值, xi0是最佳值, maxi(mini)是参数i的最大(最小)报警边界值.
按照式(2)计算的动态权重指数本质上是参数采集值偏离最佳区域的大小对健康度的影响进行的计算. 这需要理解和分析各个参数对健康状态的影响情况. 目前雷达维修专家根据长期积累的经验, 可以比较好的估计α值、最佳值、最大最小报警区间, 构成专家知识表, 能够支持本文提出的评估方法.
两个权重指数之和, 代表参数i在某个时候的全部权重指数wip:
| $w_{ip} = w_{is} + w_{id}$ | (4) |
参数的权重指数并不能应用到实际计算中去, 采用权重因子是更科学的做法. 即对各参数组成向量, 要求满足
| ${w_{{i}}} = \dfrac{{{w_{ip}}}}{{\displaystyle \sum\limits_{i = 1}^n {{w_{ip}}} }}$ | (5) |
其中, wi是参数i在一个由n个参数组成的向量中的权重因子, 说明参数i在整个向量中的重要性.
1.2 基于动态权重的健康度计算设备监测的一系列参数可以看作一个向量. 考虑以一个最健康的向量u为中心, 那么采集向量Xk到u的距离就可以看作是一个健康度的体现. 距离越大, 表示监测值越偏离健康中心, 健康度越差. 目前这样的距离算法有余弦相似度、欧式距离、马氏距离等不同的计算方法. 余弦相似度主要以向量角度偏差为目标, 不适合本研究的目标. 虽然马氏距离考虑了不同参数之间的联系, 且与参数量纲无关, 广泛用来表征设备的健康度. 但在实际使用过程中, 由于参数之间的相关性影响, 常常由于无法求协方差逆矩阵而失败, 导致其计算不稳定, 并且马氏距离还夸大了变化微小变量的作用. 很多情况下, 欧式距离成为马氏距离的后补算法. 综合考虑, 本文采用加权标准欧式距离来进行计算, 克服了普通欧式距离的缺点, 具有较好的效果且计算量小. 其计算公式为:
| ${D_k} = \sqrt {\displaystyle \sum\limits_{i = 1}^n {\dfrac{{{{({x_{ki}} \times {w_{ki}} - u)}^2}}}{{\delta _i^2}}} } $ | (6) |
其中, 假设在n个参数构成的向量Xk中, wki是向量中参数i对应的权重因子, xki是向量Xk中参数i的采集监测值. 健康向量u通过专家经验构建. δi2是参数i的方差, 实际上反映了参数i的波动性. 为了比较准确地计算实时采样方差, 采用文献[21]提出的迭代法, 可以迭代计算自从监测以来的各参数方差, 且计算量少, 在此不再详述.
直接计算出来的距离值Dk还不是设备的健康度. 考虑到距离越大, 设备健康越差; 而一般设备越不健康, 健康度数值越低. 因此使用负向函数, 将计算得到距离换算为健康度. 假设针对某个向量计算的距离值为D, 根据文献[18]可得如下公式:
| $Ehealth = A\left(\frac{{{D^h} - D}}{{{D^h} - {D^l}}}\right){e^{b.\left(\frac{{{D^h} - D}}{{{D^h} - {D^l}}} - l\right)}}$ | (7) |
其中, Dh和Dl是所有计算得到距离上下限. A是健康度范围, b是形状参数, 当b=0是表示线性处理. 按照一般处理经验, 如果Dl=0, A=100, b=0, 式(6)可以简化为:
| $E_{\rm health}^{'} = 100({D^h} - D/{D^h})$ | (8) |
某型雷达发射机由射频放大装置、调制柜、高频柜及冷却系统构成. 其中调制柜和高频柜是发射机的核心部分, 包括整流电源分机、发射监控分机、充电控制分机、可控硅调制分机、磁场电源分机、灯丝电源分机、注电源分机等若干部分构成. 系统每6 s采集20个表征发射机健康状态的监测参数. 利用这些参数进行健康度评估过程如图2所示.

|
图 2 雷达发射机健康度评估过程 |
整个过程分为3步进行, 分别说明如下:
① 根据主成分分析法, 决定需要参与健康度评估的监测参数. 然后按照专家经验, 确定参数的最优值、最大最小范围及其静态权重指数、动态权重参数等信息, 作为数据分析的依据.
当获取监测参数时, 对这些参数进行预处理. 主要预处理过程包括参数的平滑处理、归一化处理, 以及参数值的合理性检查和剔除异常数据.
② 权重因子计算. 根据前面的式(1)修正静态权重, 根据式(2)计算动态权重, 利用式(4)、式(5)计算各个参数的权重因子.
③ 健康度的计算. 利用式(6)计算加权标准欧式距离, 然后利用式(8)计算实时健康度.
考虑步骤②③前面已经介绍很清楚, 下面重点介绍步骤①的各种处理.
2.2 雷达发射机监测参数的确定利用主成分分析法确定参与健康度计算监测参数. 主成分分析(Principal Component Analysis, PCA)是一种用于高维数据降维的技术. PCA可以把可能具有线性相关性的高维变量合成为线性无关的低维变量. 新的低维数据集会尽可能的保留原始数据的特征, 从而达到降维的目的. 假设有M个N维数据需要进行降维处理, PCA算法步骤如下所述:
① 将原始数据按列组成N行M列矩阵X;
② 对X的每一行进行零均值化;
③ 计算出均值化矩阵X的协方差矩阵C;
④ 求出C的特征值及对应的特征向量;
⑤ 将特征向量按对应特征值大小从上到下按行排列成矩阵, 取前k行组成矩阵P;
⑥ Y=PX即为降维到k维后的数据.
经过PCA降维之后的数据有11个, 利用专家经验可以估计其最佳值、预警边界值、动态权重参数等信息. 雷达发射机选择的监测参数的重要信息如表1所示. 表1中, αmax和αmin分别表示某个参数正向和负向偏离时的动态权重指数函数底数值, ws则表示当前静态权重. 由于权重最后要进行归一化处理, 这些经验参数只需要相对值合理就行, 降低了专家知识要求难度.
| 表 1 监测参数重要信息表 |
2.3 数据预处理过程
在实时采集的监测参数中, 由于传感器的不稳定性或者人为因素, 可能造成个别数据不切实际, 这种数据称为异常值; 另外在采集数据过程中, 也会不可避免地叠加上噪声干扰, 影响数据质量, 因此必须进行平滑处理, 消除噪声干扰. 下面简要说明处理过程.
(1)平滑处理. 为了过滤监测参数的噪声, 采用平滑处理可以减少噪声影响, 并将数据的周期趋势表现出来. 本文采用简单的指数加权平均算法, 运算量少, 且具有不错的效果.
| $ v_t = \beta v_{t - 1} + (1 - \beta )\theta_t $ | (9) |
其中, θt是t时刻采集的参数值; vt是要代替的估计值, 即t时刻的指数加权平均值. β是一个权重参数(0 < β < 1). 一般令 β=0.9. β越小, 噪声越多, 虽然可以很快适应参数的变化, 但是容易出现异常值; β越大, 得到的结果越平滑,
但是对参数变化的适应慢. 一般需要根据参数的实际情况进行调节, 得到最佳效果.
(2)剔除异常值. 基本思想是规定一个置信限度, 凡是误差超过该限度的值, 认为是异常值, 需要剔除免于处理. 用一阶差分法来进行异常值剔除处理. 具体思路是用两个测量值来预估新的测量值, 然后与实际测量值进行比较. 如果大于设定的阈值, 则认为是异常值, 给予剔除处理.
| $ x_n^{'} = x_n - 1 + (x_{n - 1} - x_{n - 2}) $ | (10) |
| $ \left| {x_n - x_n^{'}} \right| < \phi $ | (11) |
式(10)计算出参数当前估计值
采用Python语言编程实现了上述算法. 使用了Pycharm开发调试工具, 运行在Windows 10操作系统下. 测试过程使用了前面表1选择的11个参数, 利用了其专家知识表中的信息. 考虑到实际监测的数据没有包含所有健康状态的情况, 根据分析需要, 对部分参数的监测值进行了模拟仿真, 以检查算法对各种健康度计算的适应性. 这样产生了多组测试数据, 分别对应健康、注意、报警、故障等4种状态. 表2选择了其中具有代表性的八组数据来进行分析.
| 表 2 用于测试分析的采集数据及其权重因子向量表 |
在表2中, 采集数据向量X表示由11个采用数据组成的向量, 各个数据含义与表1中的参数名称顺序一致, 如第一个数据是钛泵电流、第二个是灯丝电流…依次类推. 权重指数向量W则是按照公式(4)对静态和动态权重指数进行相加后结果, 可以直观看出各个参数的当前相对比重. 表中对偏移最佳值较多的数据用下划线加粗给予重点标识, 其对应的权重指数也一样标识, 便于识别. 可以明显看出, 某个采集数据偏离正常值越多, 其对应的权重因子占比增大. 数据组1、2是健康数据, 其权重主要体现的是静态权重的影响. 3、5、7仅有一个参数处于不同的健康状态, 而数据组4、6、8则有2个以上的参数相对最佳值偏移量较大. 其对应4个类别的健康状态是专家评定的. 从表2可明显看出, 偏移最佳值越多, 其权重指数越大, 表示这些偏差比较大的参数对整个健康度的影响占比就越大.
为了体现动态权重的计算对健康度准确评估的重要影响, 对各种情况下的健康度计算做一个对比, 即分别用标准欧式距离H1、纯静态权重标准欧式距离H2及综合静态和动态权重标准欧式距离H3进行评估, 结果与专家评估的健康度H对比, 其结果如表3和图3所示.
所有评估结果都是按照式(6)~式(8)计算出来的健康度数据. 计算H1时, 令式(6)的wki固定为1; 在计算H2时, 令式(4)的wip等于wis, 忽略动态权重的计算, 后面的计算过程没有变化; 而H3的计算则完全按照前面的描述进行. 专家评估的结果是根据采集数据的情况由专家综合评定的健康度.
从表3可以看出, H3的值与专家评估的健康度最贴合. 而不使用动态权重或者只使用静态权重指数都很难体现准确的健康状态. 相对来说, 某组偏离正常值的数据成员越多, 其不同健康度评估结果相对比较接近. 说明在没有使用动态权重计算时, 如果只是某个参数影响的整个健康状态, 很难得到准确健康度, 甚至很难体现该组数据所代表的健康状态. 图3通过折线图的方式, 更加直观的体现出这个结论.
| 表 3 在不同方法下的健康度评估对比表 |

|
图 3 不同方法健康度评估对比图 |
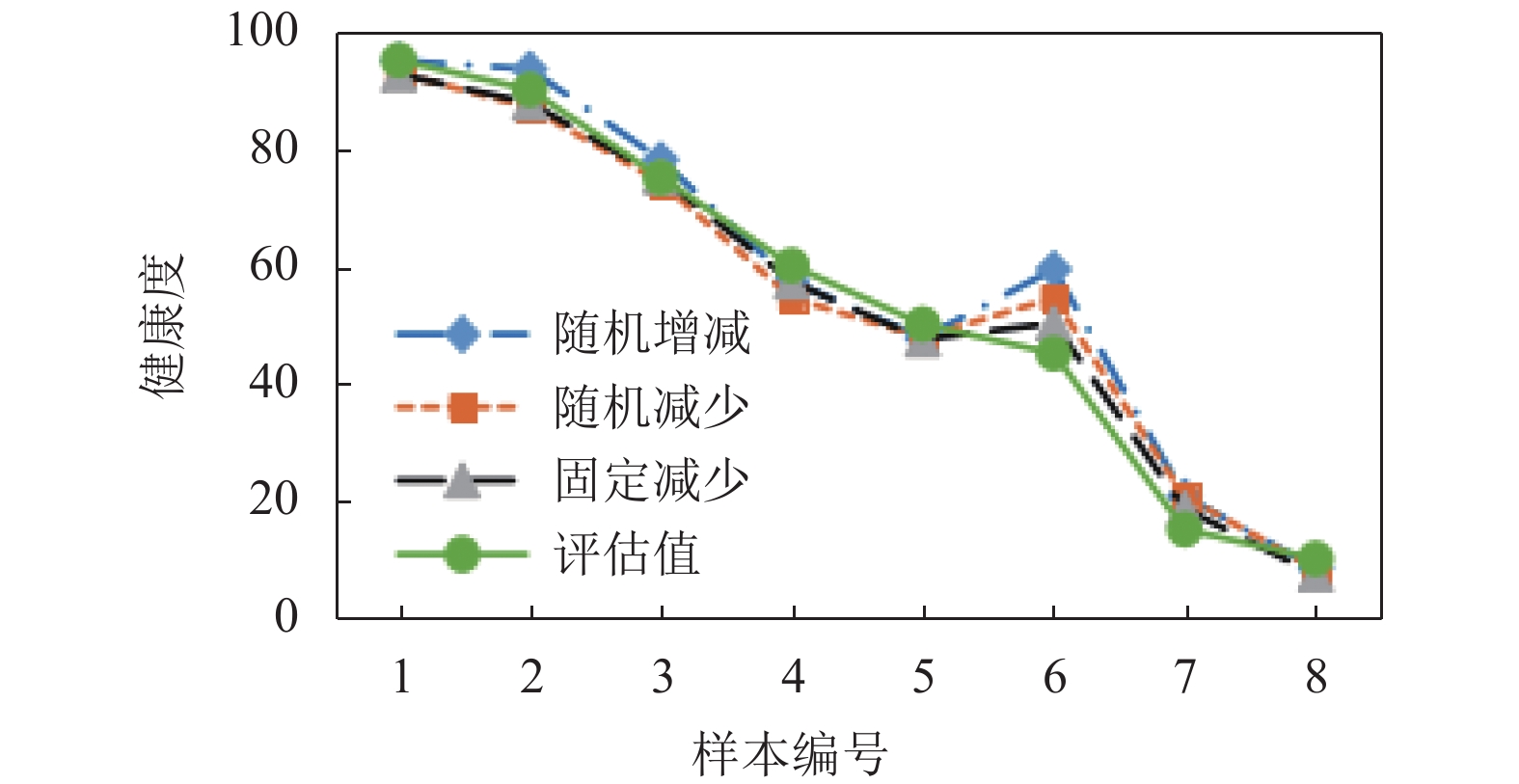
为了检验专家知识不准确对计算结果的影响, 我们有意修改表1的专家知识表中αmax和αmin的值. 总共修改了3组, 其中一组随机放大或缩小30%, 一组在30%范围内随机减小, 一组是整体等比例减小30%. 其他数据保持不变, 为了方便比较, 图中保留专家评估值, 结果如图4所示.
|
图 4 修改α值的健康度评估对比图 |
从图4可以看出, 随机增减的一组影响最大, 其次是随机减少, 而固定减少则基本和评估值保持一致, 仅有比较小的差异. 即使影响最大的一组, 也只是部分地方误差大, 实际上随机增减较容易让某些参数的动态权重和对应的健康状态不匹配, 计算的健康度误差也会比较大. 总的来说, 在30%的偏差下, 综合计算偏差在可接受范围内. 表明对专家预估的权重指数要求并不很高, 从而表明该方法具有一定实用性.
4 结束语本文根据某型雷达发射机的实际情况, 提出了一种根据监测参数值的变化影响动态权重指数的计算模型, 并利用加权标准欧式距离来准确计算设备健康度的方法. 通过专家经验设定了指数模型的参数之后, 可以突出偏离健康区间比较大的参数的权重比例, 从而让少量参数恶化导致的设备健康状态变差的情况在设备整体健康度计算上得到合理反映. 测试分析表明, 本方法具有较好的准确性, 对于评价复杂设备的健康程度是可行合理的, 具有一定的使用价值.
在具体实施过程中, 本方法的准确性依赖专家对有关参数的理解和经验, 这在一定程度上限制了本方法的广泛应用. 下一步将根据采集的健康向量标记数据, 利用核密度估计算法, 结合数值优化算法自动评估和优化动态权重评估需要的相关专家经验值, 这样可减少对专家知识的依赖, 还可以自适应不同工作状态下相关参数变化, 让本方法具有更好的适应性.
| [1] |
谭治学. 雷达发射机健康状态评价及预测技术研究[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2013.
|
| [2] |
李硕, 徐国平, 蔡兴雨, 等. 雷达装备健康状态评价方法研究. 火控雷达技术, 2017, 46(1): 12-15, 28. DOI:10.19472/j.cnki.1008-8652.2017.01.004 |
| [3] |
尹明, 叶晓慧, 李桥敏, 等. 基于证据融合的雷达发射机健康评估. 海军工程大学学报, 2015, 27(5): 48-51. DOI:10.7495/j.issn.1009-3486.2015.05.011 |
| [4] |
曹正洪, 沈继红. 基于模糊集理论的传感器健康度评价方法. 电机与控制学报, 2010, 14(5): 79-83, 90. DOI:10.15938/j.emc.2010.05.017 |
| [5] |
刘志文, 董旭柱, 吴争荣, 等. 基于多种测度的配电网关键设备在线状态评估. 电力系统及其自动化学报, 2018, 30(11): 52-57. DOI:10.3969/j.issn.1003-8930.2018.11.009 |
| [6] |
吕建伟, 余鹏, 魏军, 等. 舰船装备健康状态评估方法. 海军工程大学学报, 2011, 23(3): 72-76. DOI:10.3969/j.issn.1009-3486.2011.03.016 |
| [7] |
雷亚国, 贾峰, 周昕, 等. 基于深度学习理论的机械装备大数据健康监测方法. 机械工程学报, 2015, 51(21): 49-56. DOI:10.3901/JME.2015.21.049 |
| [8] |
张春, 舒敏. 基于支持向量机的健康状态评估方法. 计算机系统应用, 2018, 27(3): 18-26. DOI:10.15888/j.cnki.csa.006285 |
| [9] |
颜文涛, 陈朝晖, 何强, 等. 城市污水管道预报健康度评价模型及其应用研究. 中国给水排水, 2009, 25(7): 97-101. DOI:10.3321/j.issn:1000-4602.2009.07.026 |
| [10] |
刘博元, 王焕钢, 范文慧, 等. 基于大数据的复杂生产线系统健康度实时评估方法. 清华大学学报(自然科学版), 2014, 54(10): 1377-1383. DOI:10.16511/j.cnki.qhdxxb.2014.10.021 |
| [11] |
杨森, 孟晨, 王成. 基于模糊SVDD的电子装备状态评估模型研究. 计算机工程与设计, 2013, 34(2): 676-680. DOI:10.3969/j.issn.1000-7024.2013.02.055 |
| [12] |
吴魁, 孙洁, 蒋波, 等. 基于LSTM的风洞设备健康状态评估方法研究. 计算机测量与控制, 2018, 26(3): 288-291. DOI:10.16526/j.cnki.11-4762/tp.2018.03.071 |
| [13] |
谷梦瑶, 陈友玲, 王新龙. 多退化变量下基于实时健康度的相似性寿命预测方法. 计算机集成制造系统, 2017, 23(2): 362-372. DOI:10.13196/j.cims.2017.02.015 |
| [14] |
宋登巍, 吕琛, 齐乐, 等. 基于健康基线和马氏距离的液压系统变工况健康评估. 系统仿真技术, 2017, 13(3): 201-208. DOI:10.16812/j.cnki.cn31-1945.2017.03.004 |
| [15] |
焦嵩鸣. 基于融合相似度的制粉系统健康预警及故障诊断. 系统仿真学报, 2018, 30(2): 595-604. DOI:10.16182/j.issn1004731x.joss.201802028 |
| [16] |
许刚, 王珅, 王志红, 等. 基于权重分析的灰色关联度法在供水管网健康度评价中的应用. 给水排水, 2014, 40(7): 164-167. DOI:10.13789/j.cnki.wwe1964.2014.0189 |
| [17] |
赵仙保, 宣征南, 韩念琛. 基于相对健康度模型的齿轮箱运行状态综合评价. 机械传动, 2019, 43(2): 26-29, 93. DOI:10.16578/j.issn.1004.2539.2019.02.005 |
| [18] |
李鑫, 刘莹莹, 李赣华, 等. 基于模糊变权原理的卫星健康评估方法. 系统工程与电子技术, 2014, 36(3): 476-480. DOI:10.3969/j.issn.1001-506X.2014.03.12 |
| [19] |
彭炎亮, 李汪根, 刘娇, 等. 基于动态权重和模糊综合评判法的健康评估模型. 计算机系统应用, 2017, 26(1): 37-43. DOI:10.15888/j.cnki.csa.005503 |
| [20] |
王维, 齐玉玲. 基于大数据分析的列车健康度诊断方法. 电力机车与城轨车辆, 2018, 41(6): 82-84. DOI:10.16212/j.cnki.1672-1187.2018.06.023 |
| [21] |
邓胡滨, 刘觉夫, 王耀南. 均值方差的递推算法及其应用. 计算机与现代化, 1996(4): 9-11. |
 2001, Vol. 29
2001, Vol. 29


