机器视觉被广泛地应用于自动化检测和测量的视觉系统中[1]. 在实际应用中, 精密度的局限性会导致机器视觉系统采集的图像产生各种畸变, 例如径向畸变、透视畸变等[2], 随着成像设备制造技术的不断提高, 数字图像的分辨率越来越高, 图像的畸变在检测中不容忽视, 必须对其进行矫正[3]. 图像畸变矫正技术的研究主要有两个方面: 光学机械设计上的矫正和数字图像处理上的矫正[4]. 利用光学和机械结构对镜头进行矫正存在诸多局限性, 如高精度的光学图像采集镜头价格昂贵、结构设计较为复杂等[5], 因此采用数字图像处理技术对畸变进行矫正已成为目前研究的主要方向.
在图像畸变矫正理论中, 畸变模型的确立是畸变矫正的理论基础, 也是相机标定的主要内容, 而对于参考模型的选取将直接影响到畸变图像矫正的效果[6]. 目前在研究中的畸变模型各有优缺点, 比如Fitzgibbon模型[7]包含未知参数少, 计算量小但精度不高; Brown模型[8]和Heikkila模型[9]较复杂, 虽可以较好的提高图像矫正精度, 但算法计算的复杂性与工作量也成倍增加[10]. 因此, 需要根据实际情况合理规划建立摄像头的畸变模型, 达到实验设计目的.
目前常用的软件开发平台有: HALCON、Vision Pro、OpenCV和LabView等[11]. 其中LabView采用图形化编程方式, 软件开发周期短, 特别适合工控及自动化测试场合, 能够快速完成视觉系统的模型建立, 提高测试效率[12]. 因此, 本文以PCB板为研究对象, 结合径向畸变和切向畸变, 使用了一种多项式畸变成像模型, 基于LabView平台和NI Version模块采用校准点阵对机器视觉系统进行校准, 利用双线性插值算法对图像畸变进行矫正, 并对矫正结果进行对比分析得出结论.
1 图像畸变模型的建立理想条件下, 机器视觉成像系统可以被抽象为小孔成像模型, 镜头的图像畸变可以忽略不计. 然而实际并非理想, 镜头本身特性的不完美性对成像的最终结果造成的影响是不可忽视[13].
1.1 畸变模型的确立本文在图像畸变的矫正主要研究径向畸变和切向畸变, 径向畸变是由于现实中镜头所用的凸透镜或凹透镜组合固有的光学特性, 导致真实坐标点沿着像面径向产生的偏移. 切向畸变与径向畸变的影响不同, 切向畸变是使图像像素沿着切线方向变形, 如将矩形变为梯形图像[14].
根据泰勒级数定义和镜头在畸变中心处不会产生畸变, 以及径向畸变是沿畸变中心对称的特性, 径向畸变数学模型表示式为:
| $\left\{ {\begin{split} & {{x_{\rm corrected}} = x\left( {1 + {k_1}{r^2} + {k_2}{r^4} + \cdots + {k_n}{r^{2n}}} \right)} \\ & {{y_{\rm corrected}} = y\left( {1 + {k_1}{r^2} + {k_2}{r^4} + \cdots + {k_n}{r^{2n}}} \right)} \end{split}} \right.$ | (1) |
式中, r为理想中像素点到原点的距离, (x, y)为畸变点在图像的原始坐标, 即
切向畸变的数学模型表示式为:
| $\left\{ {\begin{array}{*{20}{c}} {{x_{\rm corrected}} = 2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)} \\ {{y_{\rm corrected}} = 2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)} \end{array}} \right.$ | (2) |
式中, (x, y)为图像畸变像素点在相机图像平面的原始坐标位置; (xcorrected, ycorrected)为矫正后的新坐标位置, p1, p2为描述切向畸变的待定系数.
本文结合式(1)和式(2)采用的多项式畸变模型表达式为:
| $\left\{ {\begin{array}{*{20}{c}} \begin{split} {x_{\rm corrected}} = &x\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right) \\ &+\left[ {2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)} \right] \end{split} \\ \begin{split} {y_{\rm corrected}} =& y\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right) \\ &+\left[ {2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)} \right] \\ \end{split} \end{array}} \right.$ | (3) |
式中, k1
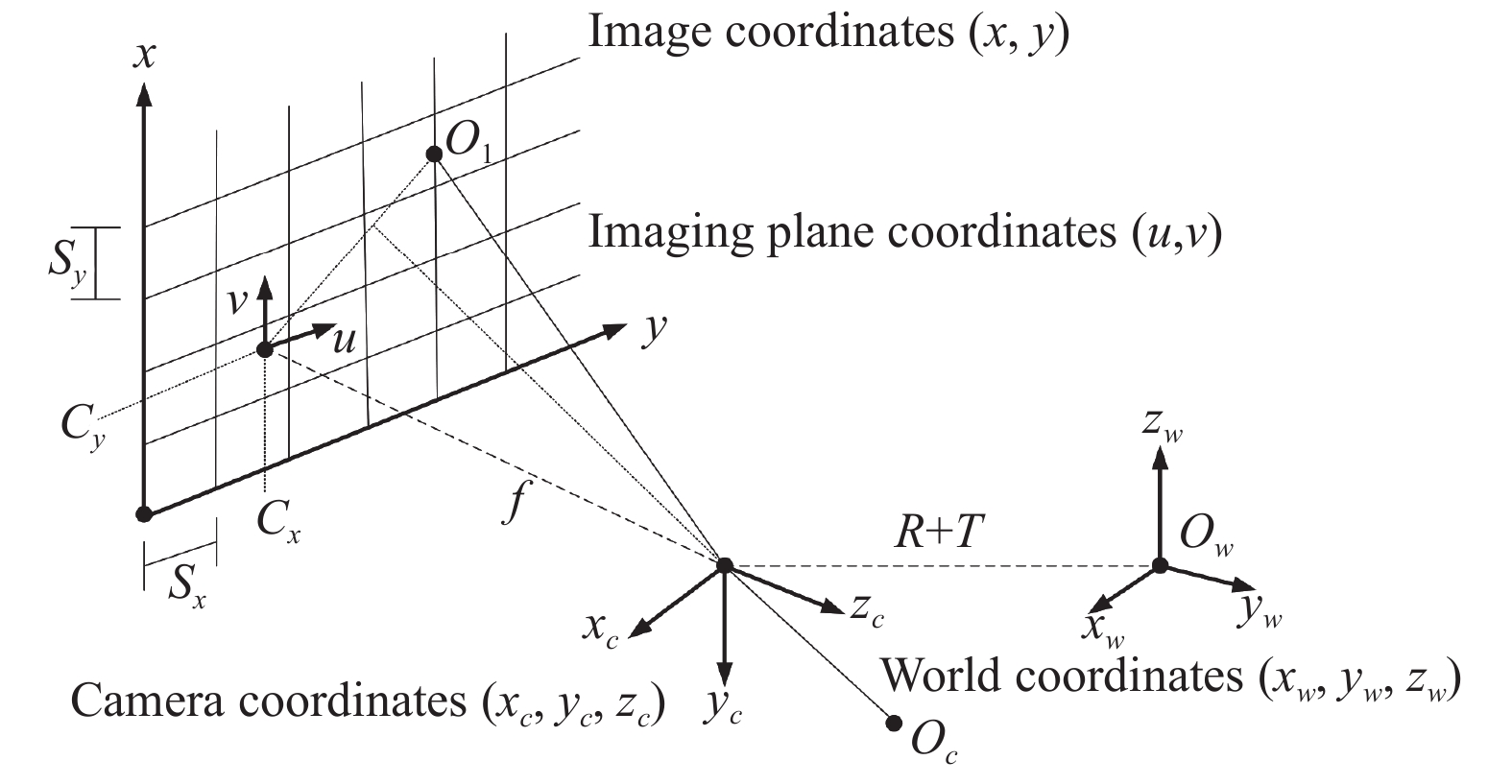
本文对畸变模型的研究建立4种计算机视觉坐标系: 世界坐标系、相机坐标系、成像平面坐标系和图像坐标系, 坐标系统转换模型示意图如图1. 不难看出, 真实世界坐标系与相机坐标系之间的变换可以通过旋转和平移来实现.
|
图 1 坐标系统转换模型示意图 |
世界坐标系在平移T后, 先沿z轴旋转
| $\left[ {\begin{array}{*{20}{c}} {{x_c}} \\ {{y_c}} \\ {{{\textit{z}}_c}} \end{array}} \right] = {{R}}\left[ {\begin{array}{*{20}{c}} {{x_w}} \\ {{y_w}} \\ {{{\textit{z}}_w}} \end{array}} \right] + {{T}} = \left[ {\begin{array}{*{20}{c}} \psi &\varphi &\theta \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_w}} \\ {{y_w}} \\ {{{\textit{z}}_w}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{t_x}} \\ {{t_y}} \\ {{t_{\textit{z}}}} \end{array}} \right]$ | (4) |
其中, R为旋转矩阵, 与
若不考虑镜头畸变影响, 成像点可有相机坐标系投影得到:
| $\left[ {\begin{array}{*{20}{c}} u \\ v \end{array}} \right] = \frac{f}{{{{\textit{z}}_c}}}\left[ {\begin{array}{*{20}{c}} {{x_c}} \\ {{y_c}} \end{array}} \right]$ | (5) |
式中, f为相机焦距, 图像坐标系和成像平面坐标系转换关系为:
| $ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \frac{f}{{{{\textit{z}}_c}}}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\dfrac{1}{{{s_x}}}}&0&{{x_0}} \end{array}}\\ {\begin{array}{*{20}{c}} 0&{\dfrac{1}{{{s_y}}}}&{{y_0}} \end{array}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v\\ u\\ 1 \end{array}} \right],{f_y} = \dfrac{f}{{{s_y}}},{f_x} = \dfrac{f}{{{s_x}}} $ | (6) |
其中, (x, y)为图像像素坐标, Sx, Sy分别为每个像素在两个坐标轴上的物理尺寸, (x0, y0)为光轴与像平面交点在图像坐标系中的坐标, fx, fy为成像平面上的等效焦距.
设Ow中的zw = 0, 可以得出:
| $\begin{array}{l} k\left[ {\begin{array}{*{20}{c}} \!\!x\!\!\\ \!\!y\!\!\\ \!\!1\!\! \end{array}} \right] = {{M}}\left[ {\begin{array}{*{20}{c}} \psi\!\!\!\!\! & \varphi\!\!\!\!\! & \theta \!\!\!\!\!&{{T}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \!\!{{x_w}}\!\!\\ \!\!{{y_w}}\!\!\\ \!\!0\!\!\\ \!\!1\!\! \end{array}} \right] = {{M}}\left[ {\begin{array}{*{20}{c}} \psi\!\!\!\!\! & \varphi\!\!\!\!\! &{{T}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \!\!{{x_w}}\!\!\\ \!\!{{y_w}}\!\!\\ 1 \end{array}} \right] \end{array}$ | (7) |
| ${{M}} = \left[ {\begin{array}{*{20}{c}} {{f_r}}&\gamma &{{r_0}} \\ 0&{{f_c}}&{{r_c}} \\ 0&0&1 \end{array}} \right]$ | (8) |
式中, k为比例系数, M为相机内部参数矩阵.
设 H为单应性矩阵, 令:
| ${{H}} = \left[ {\begin{array}{*{20}{c}} {{h_1}}&{{h_2}}&{{h_3}} \end{array}} \right] = {{M}}\left[ {\begin{array}{*{20}{c}} \psi &\varphi &{{T}} \end{array}} \right]$ | (9) |
由旋转矩阵R的
| $\left\{ {\begin{array}{*{20}{l}} {h_1^{\rm T}{{{M}}^{ - {\rm T}}}{{{M}}^{ - 1}}{h_2} = 0} \\ {h_1^{\rm T}{{{M}}^{ - {\rm T}}}{{{M}}^{ - 1}}{h_1} = h_2^{\rm T}{{{M}}^{ - {\rm T}}}{{{M}}^{ - 1}}{h_2}} \end{array}} \right.$ | (10) |
只要采集的图像有足够的图像和物理空间的对应点, 就可以求出H, M矩阵中只有5个未知量, 当采集的图像至少为3幅时, 就可以根据建立的约束方程求出M矩阵中的内参数. 由式(7)进一步得到相机视觉模型的外参数
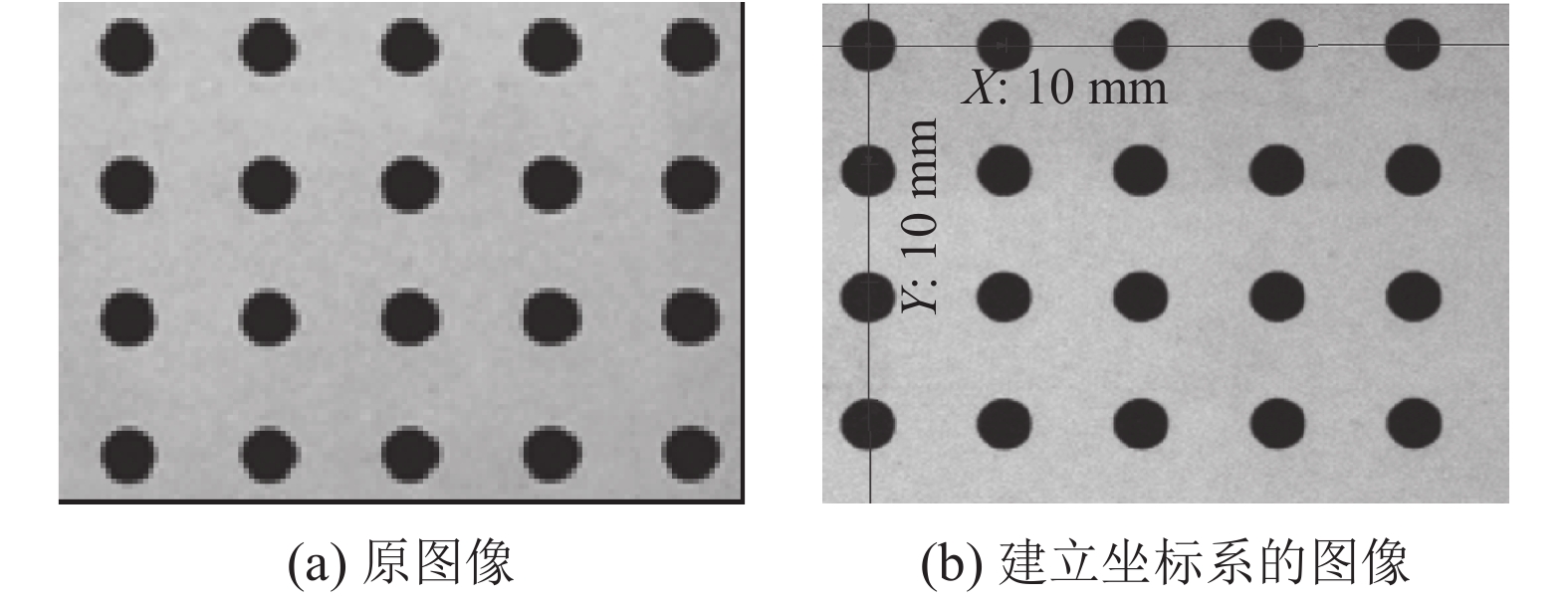
本文图像选用德国Basler acA系列相机及其配套镜头采集, 且按上述坐标系之间的转换, 结合多项式畸变模型和2.2节的公式基于LabView和NI Version软件平台建立坐标系. 设计满足实验要求的15×15圆点阵列, 并粘在一张光滑平板上. 相邻水平点、垂直点的中心间距均为10 mm, 点直径4 mm. 其中主要采集模板中的4×5点阵. 建立的坐标系如图2.
|
图 2 坐标系建立前后图 |
在进行坐标转换时涉及的点数较多, 本文选取图像中的其中20个点的坐标, 依据上述坐标系之间的转换关系, 得出转换结果如表1.
| 表 1 多项式畸变成像模型坐标转换参数 |
由各点的转换结果, 可得: 最大误差为0.010848; 计算平均误差为0.008485; 标准差为0.000449. 也证实了: 实际坐标和图像坐标的转换通过这一步骤, 可以实现较小误差的精确转换.
2 机器视觉系统校准在机器视觉系统中, 系统校准是指利用包含多个点的标准模板, 为系统提供真实世界坐标系中多个坐标点的已知信息[15]. 有了这些信息, 就可以结合成像系统模型, 获得图像总各像素点与真实世界之间的线性或非线性的映射关系, 如将这些信息应用到后续的图像采集中, 就可以降低各种畸变对系统检测结果的影响, 并可对畸变图像进行矫正.
2.1 系统校准方法分析日前在LabView平台研究常用的系统校准方法有: 简易系统校准法、透视校准和校准点阵校准. 简易系统校准法和透视校准是两种通过手工输入已知信息点就可以实现系统校准的方法, 在实践工程中, 若镜头存在径向或切向畸变, 手工输入已知信息点的校准方法就相对麻烦和效率低下[16]. 本文采用校准点阵为校准过程提供信息点输入的工具, 对系统进行校准.
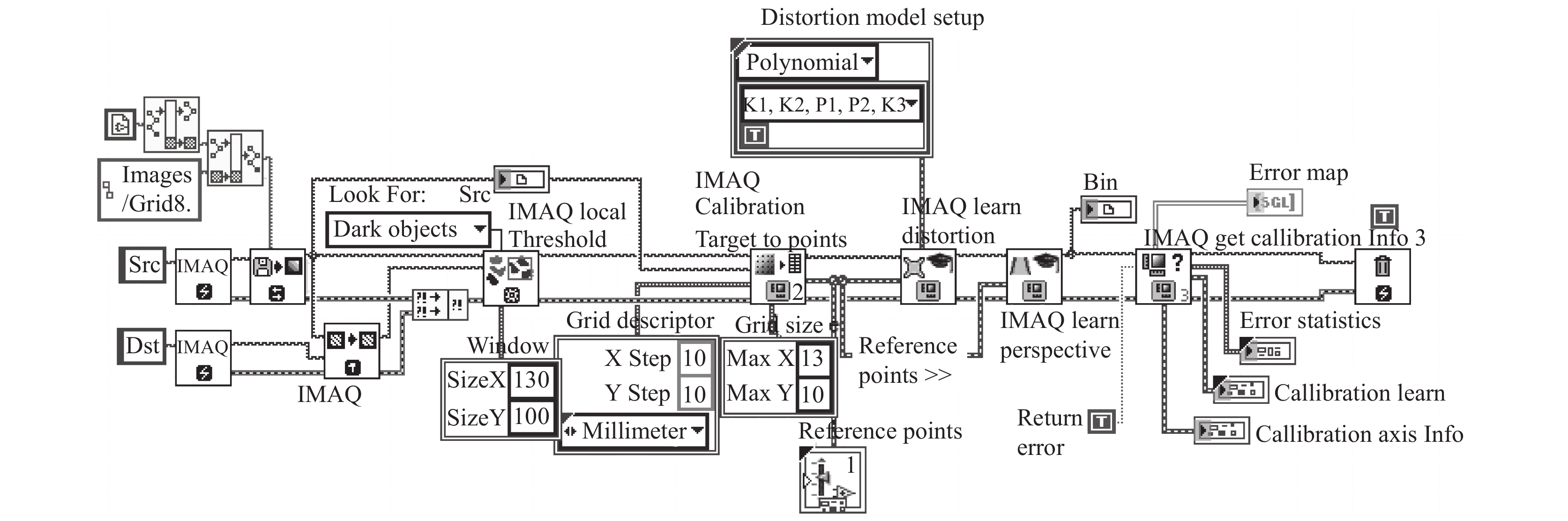
2.2 基于LabView平台的系统校准这里采用上文中的多项式畸变成像模型的机器视觉系统采用校准点阵, 在实验室的LabView平台上进行程序设计和图像校准. 校准程序界面如图3.
|
图 3 图像校准程序界面 |
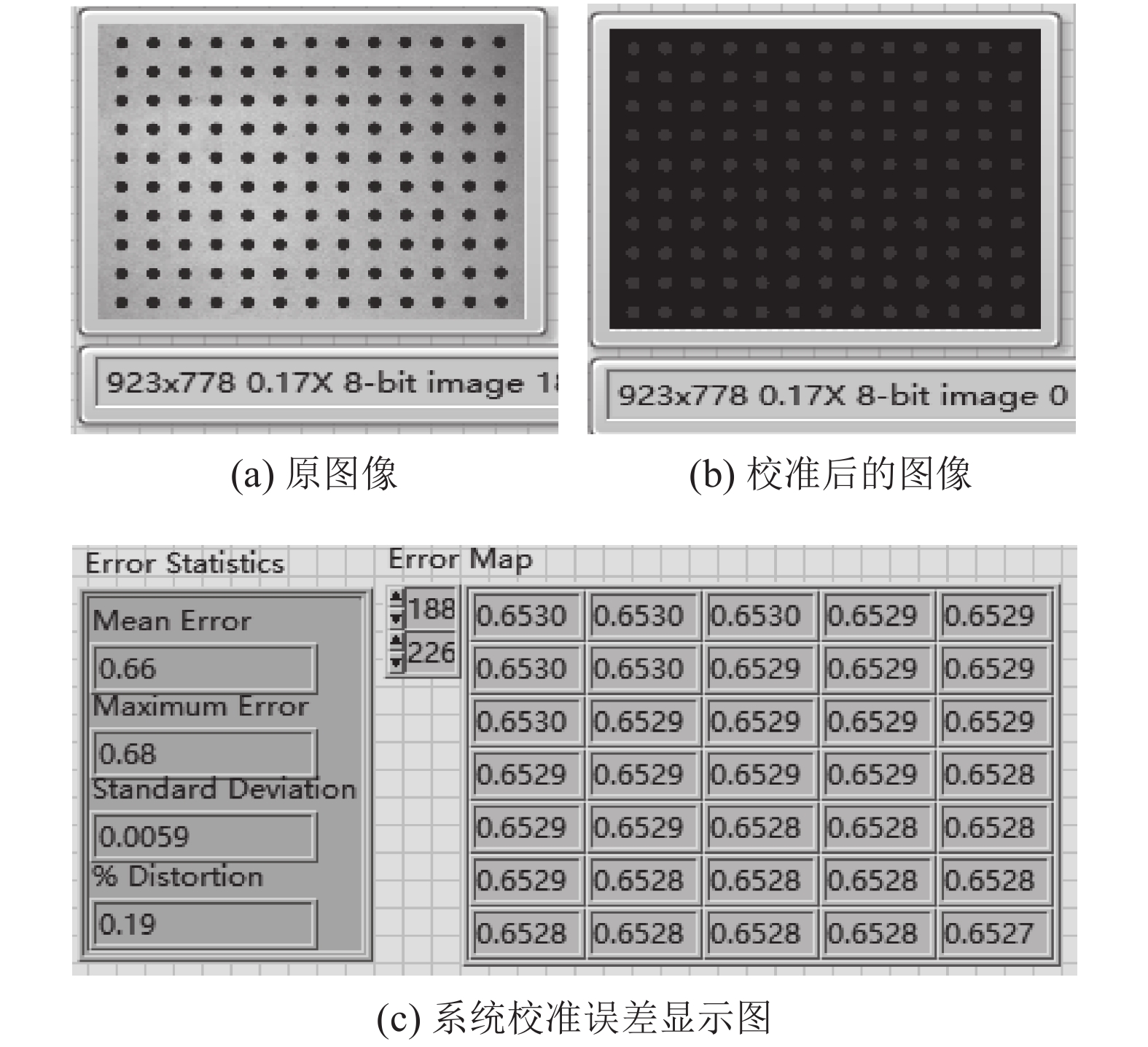
校准图和校准结果如图4. 在LabView中通常采用误差映射表(error Map)、畸变率(distortion)、平均误差(mean error)、最大误差(maximum error)以及标准差(standard deviation)等相关信息来衡量判断系统校准的质量. 误差映射表表示产生畸变像素与真实位置之间的距离, 其值越小, 说明计算得到的真实世界的坐标越精确; 畸变率主要用来说明采集的图像相对于正常图像的变形情况, 等于像素位置误差占像素到光心位置所对应像素距离的百分比, 本质上属于相对误差, 在机器视觉系统中, 一般要确保畸变率小于1%.
|
图 4 图像校准前后对比以及误差参数图 |
由系统校准结果图4(c)可见: 误差映射表(error map)为0.6530; 均误差(mean error)为0.66; 畸变率(distortion)为0.19%, 达到较好的校准结果.
3 图像畸变矫正算法经过系统校准后, 可对采集图像进行一定的畸变的矫正, 在机器视觉系统中, 图像的坐标值都是整数离散的, 处理后的图像坐标信息往往与原图像的位置坐标并不一一对应, 这就会导致图像矫正完的坐标对应原图有可能出现不是整数点, 因此, 就需要用到图像插值算法[17], 进一步提高图像的清晰度.
3.1 图像矫正算法图像矫正的方法目前主要有: 0阶插值算法、双线性插值算法、三次卷积插值算法[18]. 0阶插值算法是根据就近原则, 利用距离目标点最近的像素点来代替目标点, 该算法计算便捷快速, 但会产生较为严重的失真, 无法满足清晰度要求较高的图像处理; 双线性插值算法通过在水平和垂直两个方向均进行线性插值来确定新图像中像素值, 处理后图像缩放质量较高; 三次卷积插值算法将插值点附近的16个参考点的灰度值变化考虑在内, 利用三次分段函数多项式进行计算, 精度高但计算量较大, 且对硬件处理要求较高[19].
对比分析3种插值算法, 双线性插值法改善了灰度值离散的问题, 且兼顾满足插值精度和算法简洁性的要求. 因此, 本文的图像矫正算法采用双线性插值法.
3.2 基于LabView平台图像畸变矫正在实验室电路板检测平台上进行了搭建和对采集图像的畸变矫正, 图像矫正可以采用适应原图比例(scale to fit)和保持原图比例(scale to preserve)两种方式. 在校准程序中添加矫正模块的程序代码, 图像矫正程序界面如图5黑框内容所示.
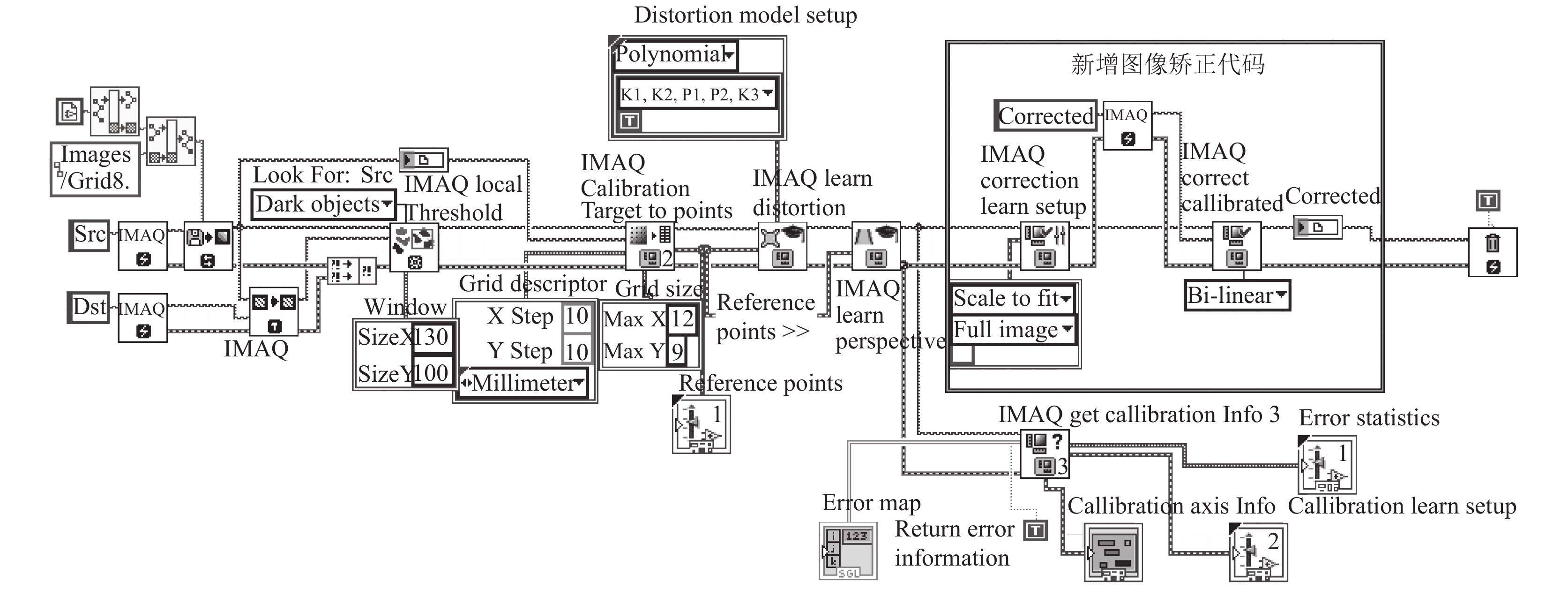
|
图 5 图像矫正程序界面 |
图像矫正的结果如图6(b)、图6(c)所示. 图像矫正的误差参数如图7所示.

|
图 6 PCB电路板图像不同方式下矫正前后对比图 |
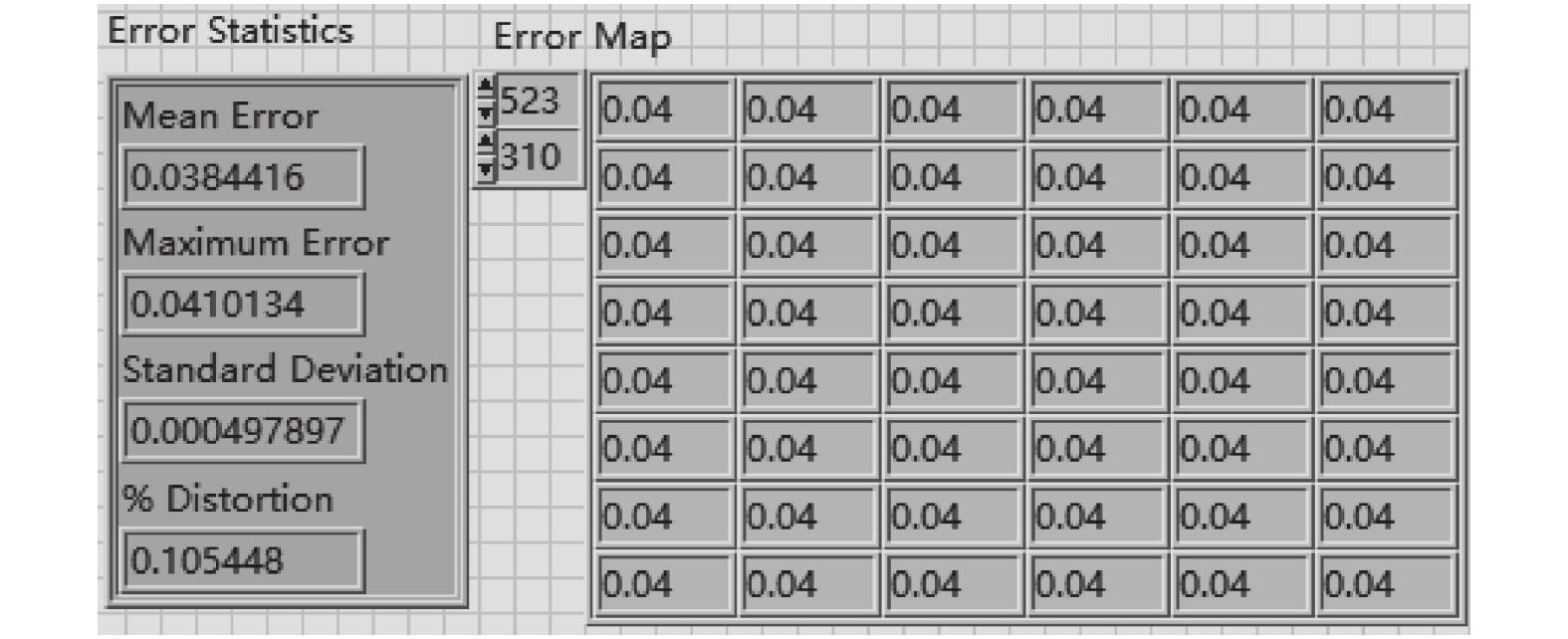
|
图 7 校准并矫正后的误差参数图 |
由此得出: (1)使用不同缩放模式对图像进行矫正, 生成的矫正图像尺寸不同; (2)在Scale to Preserve方式下生成的矫正图像要略大于源图像; (3)矫正方式的不同只对矫正后生成图像的尺寸大小有影响, 与矫正精度无关; (4)采用线性插值算法进行矫正后的图像畸变率为0.10%要小于校准后的畸变率0.19%.
4 实验结果分析本文对结论在实验室的电路板检测平台上进行验证, 取一块PCB电路板采集15幅图像, 按照设计的矫正方案, 分别采用多项式畸变模型和Heikkila模型进行畸变矫正实验, 矫正后各项误差参数见表2、表3.
得到表2、表3中15幅图像矫正后的误差映射平均值分别为0.4393、0.6487, 均畸变率为分别0.152701%和0.436 4306%, 从误差参数的平均值来看, 采用多项式畸变模型矫正误差明显较小效果更好, 满足图像矫正的处理要求; 图像矫正后像素精度达到0.01, 畸变率最小可达到0.087727%, 实现了满意的矫正效果.
5 结论本文通过分析摄像头的成像原理和图像畸变的原因, 基于LabView平台在多项式畸变模型的背景, 使用校准点阵对机器视觉系统进行校准, 用本文设计的矫正方式对图像进行矫正. 通过实验测试, 得到图像矫正后像素误差可精确至0.01, 畸变率最小可至0.087727%, 且在LabView平台中程序编写相对简单, 开发周期较短. 证明此方法较好地实现了对图像畸变的矫正, 有效消除畸变影响, 是实现精密检测中的必要手段和有效的方法.
| 表 2 多项式畸变模型的PCB图像矫正后误差参数表 |
| 表 3 Heikkila模型的PCB图像矫正后误差参数表 |
| [1] |
卢荣胜, 吴昂, 张腾达, 等. 自动光学(视觉)检测技术及其在缺陷检测中的应用综述. 光学学报, 2018, 38(8): 0815002. |
| [2] |
汤勃, 孔建益, 伍世虔. 机器视觉表面缺陷检测综述. 中国图象图形学报, 2017, 22(12): 1640-1663. DOI:10.11834/jig.160623 |
| [3] |
乔闹生, 叶玉堂, 莫春华, 等. 印刷电路板光电图像畸变校正研究. 光电子•激光, 2009, 20(11): 1548-1551. |
| [4] |
周秀荣, 崔小虹, 邢冀川. 基于LabVIEW平台的图像采集与处理技术研究. 光学技术, 2007, 33(S1): 357-358. |
| [5] |
张宝辉, 姚立斌, 张巍伟, 等. 红外图像校正与增强技术研究现状. 红外技术, 2017, 39(6): 481-488. DOI:10.11846/j.issn.1001_8891.201706001 |
| [6] |
尹丽华, 李范鸣, 刘士建, 等. 光电全景成像系统的图像校正技术. 光电工程, 2016, 43(8): 53-58. DOI:10.3969/j.issn.1003-501X.2016.08.009 |
| [7] |
Fitzgibbon AW. Simultaneous linear estimation of multiple view geometry and lens distortion. Proceedings of 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Kauai, HI, USA. 2001. 120–125.
|
| [8] |
Heikkila J. Geometric camera calibration using circular control points. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(10): 1066-1077. DOI:10.1109/34.879788 |
| [9] |
Brown DC. Close-range camera calibration. Photogrammetric Engineering, 1971, 37(8): 855-866. |
| [10] |
李光明, 孙英爽, 党小娟. 基于LabVIEW的几何匹配方法的设计与实现. 计算机工程与设计, 2016, 37(10): 2705-2709. |
| [11] |
吕金隆. 基于LabVIEW的机器视觉伺服系统开发平台的研究[硕士学位论文]. 青岛: 青岛大学, 2017.
|
| [12] |
李彤彤. 双目视觉系统的标定及畸变校正技术研究[硕士学位论文]. 长春: 吉林大学, 2019.
|
| [13] |
Tang ZW, von Gioi RG, Monasse P, et al. A precision analysis of camera distortion models. IEEE Transactions on Image Processing, 2017, 26(6): 2694-2704. DOI:10.1109/TIP.2017.2686001 |
| [14] |
张建国, 陈维光, 莘明星, 等. 一种基于LabVIEW的摄像机非线性畸变标定方法. 船舶工程, 2018, 40(12): 64-68, 76. |
| [15] |
Ronda JI, Valdés A. Geometrical analysis of polynomial lens distortion models. Journal of Mathematical Imaging and Vision, 2019, 61(3): 252-268. DOI:10.1007/s10851-018-0833-x |
| [16] |
王赛男, 孟显娇, 鲜鑫. 基于机器视觉的鱼眼镜头畸变校正算法. 数字技术与应用, 2018, 36(10): 141-142, 144. |
| [17] |
余芬芬, 金国强, 金一, 等. 基于图像处理的PCB在线检测图像校正. 工业控制计算机, 2018, 31(8): 124-126. DOI:10.3969/j.issn.1001-182X.2018.08.055 |
| [18] |
Li J, Su J, Zeng X. A solution method for image distortion correction model based on bilinear interpolation. Computer Optics, 2019, 43(1): 99-104. DOI:10.18287/2412-6179-2019-43-1-99-104 |
| [19] |
杨高科. 图像处理、分析与机器视觉(基于LabVIEW). 北京: 清华大学出版社, 2018.
|
 2001, Vol. 29
2001, Vol. 29



