人机交互的方式有很多种, 如鼠标键盘交互、触摸屏交互、语音交互、体感交互等. 手势交互作为一种新型的人机交互方式, 目前已经成为人机交互的重要方式之一. 人手作为身体上最灵活的器官, 将它作为人机交互的方式, 可以使交互更加便利、通用性能更强.

非接触式的动态手势交互已经被应用到体感游戏、辅助驾驶以及手语识别等领域, 为人们带来了简洁方便的用户体验. 但是因为手势具有时间和空间上的多样性和不确定性, 而且人手本身也是复杂的可变形体, 所以目前这种人机交互方式还处于实验阶段, 理论不是很成熟, 能够识别的范围比较小. 因此, 对动态手势的识别技术研究具有重要意义. 常用的动态手势识别方法有: 基于模板匹配的动态时间规整(Dynamic Time Warping, DTW)方法^[1,2]和基于模式识别的隐马尔科夫模型方法^[3,4]. 其中, 采用DTW方法在解决大数据量、复杂手势、组合手势识别等问题比较其他方法处于劣势^[5]; 采用隐马尔科夫模型识别手势, 该方法复杂、需要大量的训练数据^[2]并且识别总类少. 由于深度学习模型具有强大的非线性建模能力, 能够表达更高层次、更加抽象的内部特征等特点, 近年来深度学习被用于动态手势识别^[6,7]. 文献[6]结合EgoHands手势数据集, 改进深度卷积网络模型中的参数和网络结构, 对深度卷积网络模型进行训练, 得到高识别率动态手势识别模型, 识别准确率能够达到85.9%, 识别速度每秒钟可达到16.8帧. 文献[7]利用改进的多维卷积神经网络提取手势的时空特征, 融合多传感器信息并通过支持向量机实现微动手势识别, 针对多类动态手势数据集能达到87%以上的识别准确率, 并且对手势的背景和光照都具有较好的鲁棒性. 目前动态手势识别仍存在以下问题: 复杂背景干扰、指尖特征点识别和定位困难、光照环境的变化^[8], 这些问题导致了动态手势识别识别率低.

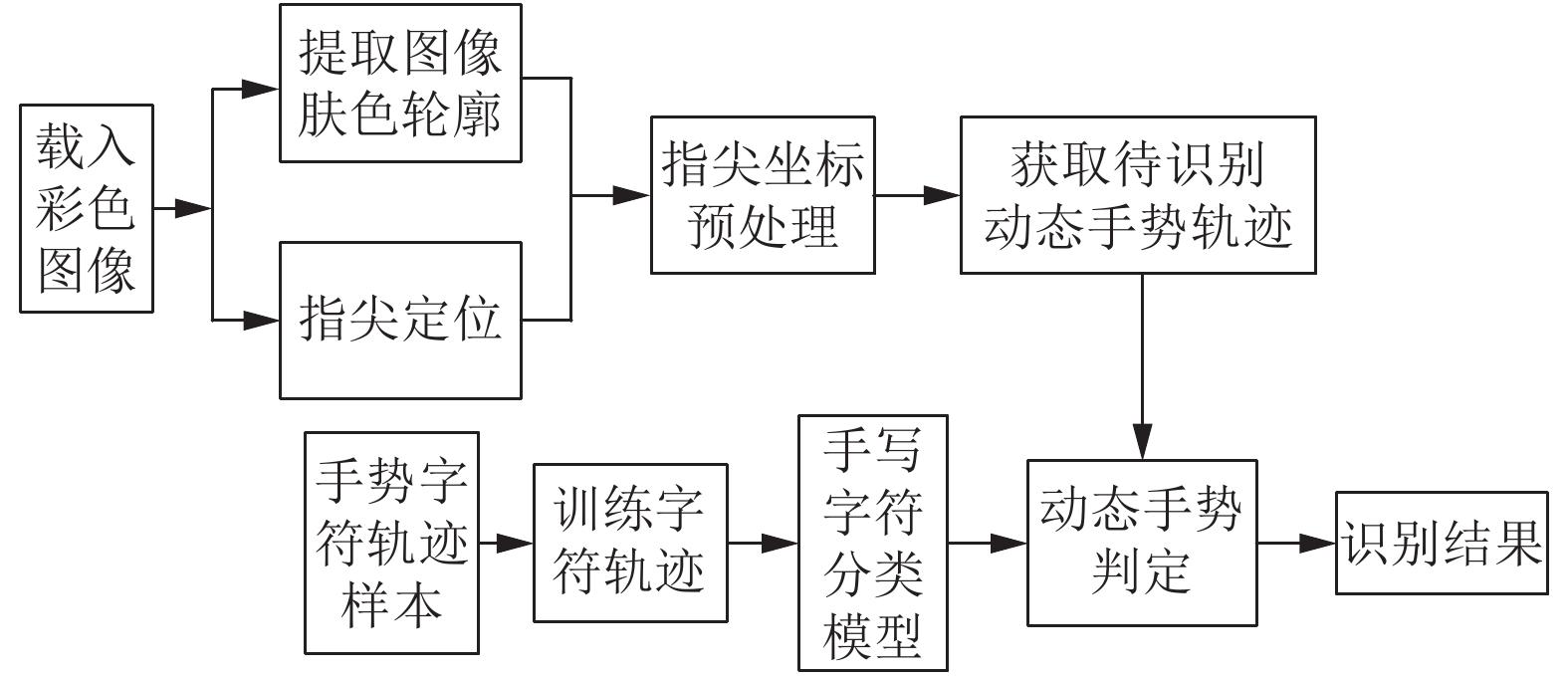
针对以上存在问题, 提出的动态手势轨迹特征提取方法能够有效排除复杂背景的干扰、指尖特征点获取和定位困难; 提出的联合CNN-Softmax-SVM的手势识别算法能够对动态手势进行有效识别, 从而大大提高了动态手势识别率. 本文中的动态手势识别系统主要流程如图1所示.

首先在HSV颜色空间下提取指尖贴纸坐标获取动态指尖重心坐标, 通过肤色分割和射线法排除肤色轮廓外复杂背景的干扰, 得到待识别的二值化轨迹图片; 其次采用CNN-Softmax和CNN-SVM对手写轨迹样本训练分别得到轨迹样本训练模型, 最后利用训练好的轨迹样本分类模型对动态手势识别.

1 动态手势特征提取 1.1 获取每帧图像指尖轨迹点

为了在复杂背景下很好地对动态手势指尖顺序轨迹点进行采集, 在指尖贴上便携式贴纸, 通过检测每帧贴纸轮廓的质心坐标来定位指尖中心点, 其中贴纸要被指尖完全覆盖. 先把每帧图像从RGB (Red, Green, Blue)颜色空间转换到HSV (Hue, Saturation, Value)颜色空间:

$\left\{ {\begin{array}{*{20}{l}} {\theta {\rm{ = }}\arccos \left( {\dfrac{{\dfrac{1}{2}[(R - G) + (R - B)]}}{{\sqrt {(R - G)(R - G) + (R - G)(G - B)} }}} \right)}\\ {V = \dfrac{1}{3}(R + G + B)\begin{array}{*{20}{c}} ;&{V \in [0,1]} \end{array}}\\ {S = 1 - \dfrac{3}{{R + G + B}}[\min (R,G,B)]\begin{array}{*{20}{c}} ;&{S \in [0,1]} \end{array}}\\ {H = \left\{ {\begin{array}{*{20}{l}} \theta, &{G \ge B}\\ {{{360}^\circ } - \theta },&{G < B} \end{array}\begin{array}{*{20}{l}} ;&{H \in [0,{{360}^\circ }]} \end{array}} \right.} \end{array}} \right.$

(1)

式中, H为色调, S为饱和度,V为明亮度. 利用式(1), 将RGB颜色空间的图像(图2(a))转换成HSV颜色空间(图2(b)). 本文所选指尖贴纸为蓝色, 设置图2(c)的HSV各个分量的阈值范围为 $H \in [{\rm{10}}{{\rm{0}}^\circ },{\rm{12}}{{\rm{4}}^\circ }]$ 、 $S \in [0.169,1]$ 、 $V \in [0.180,1]$ 得到图2(c)所示的指尖贴纸二值化图.

对图2(c)采用轮廓检测获得指尖贴纸轮廓在每一帧图上的坐标, 通过轮廓的矩计算轮廓的质心并作为指尖中心点坐标.

1.2 剔除异常轨迹点

当复杂背景中存在类贴片颜色干扰时, 仍然会被误判为指尖中心点, 因此通过判断指尖中心点是否在肤色轮廓内部, 来排除类贴片颜色的背景干扰. 在RGB空间里人的肤色受亮度影响较大, 把RGB转为YCbCr颜色空间提取肤色分量 ${C_r}$ 、 ${C_b}$ 信息, 在一定范围内可以忽略亮度分量Y的影响.

$\left\{ \begin{split} & Y = 0.299R + 0.578G + 0.114B \\ & {C_b} = - 0.169R - 0.331G + 0.5B \\ & {C_r} = 0.5R - 0.419G - 0.081B \\ \end{split} \right.$

(2)

利用式(2)提取图2(a)的 ${C_r}$ 、 ${C_b}$ 分量在 ${C_r} \in [127, 176]$ 和 ${C_b} \in [85,129]$ 范围内的值, 如图3(a)和图3(b)所示. 利用大津法(Otsu)对图3(a)和图3(b)进行自适应阈值分割, 得到相应的二值化图. 然后将 ${C_r}$ 和 ${C_b}$ 分量的二值图与操作, 则得到二值化的肤色图. 最后采用轮廓检测获取二值化肤色图的连通域轮廓坐标集合.

通过射线法判断指尖中心点是否在肤色轮廓坐标连通域内. 以待判断点的坐标点开始, 沿横坐标水平向右作射线, 判断射线与肤色轮廓交点的个数, 若为奇数则为指尖中心点如图4(a)所示, 若为偶数则为异常干扰点如图4(b)所示.

1.3 获取动态手势

首先获取每一帧图像的肤色轮廓和指尖中心点; 其次剔除背景异常点之后将每帧指尖中心点按顺序保存至数组中; 最后以第一个指尖中心点坐标为手势起始状态, 以最后一个检测的指尖中心坐标为手势结束状态, 将每一个指尖中心点按数组顺序相连, 即可构成表示该手势的运动轨迹. 如图5所示为获取数字字符“2”的动态手势, 其中图5(b)的字符轨迹包含150帧的指尖中心顺序相连, 待用于手势识别输入.

2 联合CNN-Softmax-SVM的手势识别 2.1 卷积神经网络

卷积神经网络(Convolutional Neural Networks, CNN)是一种深度前馈人工神经网络, 广泛应用于图像分类等计算机视觉问题. CNN模型主要包括卷积层、降采样层、全连接层^[9]. 卷积层由滤波器组成, 用于“滑动”输入图像的宽度和高度, 并计算输入区域的点积和权值学习参数, 提取图像的纹理特征, 实现图像特征的增强. 第m层特征图第j个神经元的输入为^[10]:

$\left\{ \begin{split} & x_j^m = f\left( {h_j^m} \right) \\ & h_j^m = \displaystyle \sum\limits_{i \in {M_j}} {x_i^{m - 1}*k_{ij}^m + b_j^m} \\ \end{split} \right.$

(3)

式中, $h_j^m$ 称为下采样层m的第j通道的净激活, 它由前一层输出特征图 $x_j^{m - 1}$ 进行下采样加权、偏置后得到; ${M_j}$ 为选取的输入特征图子集; $x_j^{m - 1}$ 为第m–1卷积层的第i个神经元的输出; $k_{ij}^m$ 是卷积核矩阵; $b_j^m$ 为第m卷积层特征图第j个神经元的偏置参数; “*”是卷积符号; $f( \cdot )$ 为激活函数, 通常可使用Sigmoid, tanh, ReLU等函数, 文中采用ReLU函数:

$f_{\rm ReLU}(X{{) = }}\left\{ {\begin{array}{*{20}{l}} {{X}},&{{\rm if}\;X > 0}\\ 0,&{{\rm if}\;X \le 0} \end{array}} \right.$

(4)

当输入经过卷积层时, 若得到的特征图仍然较大, 可以通过下采样层来对每一个特征图进行降维操作. 下采样层公式为^[10]:

$\left\{ \begin{split} & x_j^m = f(h_j^m) \\ & h_j^m = \beta _j^mdown(x_j^{m - 1}) + b_j^m \\ \end{split} \right.$

(5)

式中, β是下采样层的权重系数; $b_j^m$ 是下采样层的偏置项; 符号 $down( \cdot )$ 表示下采样函数, 它通过对输入特征图 $x_j^{m - 1}$ 通过滑动窗口方法划分为多个不重叠的n×n图像块, 然后对每个图像块内的像素求和、求均值或最大值.

提取的特征向量首先通过全连接层, 然后再通过Softmax层得到分类权重, Softmax层的函数为:

$P{S_j} = \dfrac{{{e^{{a_j}}}}}{{\displaystyle \sum\limits_{k = 1}^n {{e^{{a_k}}}} }}$

(6)

式中, ${a_j}$ 表示通过全连接层之后的向量里的第j个值, 由于 ${a_j}$ 没有范围大小, 通过Softmax函数之后得到的 ${P_j}$ 为类别的概率, 范围在0–1之间; n为待输出总类数; $e$ 为欧拉常数.

2.2 支持向量机

支持向量机(Support Vector Machine, SVM)^[11]是一种机器学习算法, 通过将输入向量映射到一个高维的特征空间, 在这个空间中构造最优分类面, 从而达到两类或者多类的样本划分, 在多数情况下, SVM比CNN全连接层的线性分类泛化能力好^[12].

设样本集为 $({u_i},{v_i}),i = 1,2, \cdots, n, {u_i} \in {R^d},{v_i} \in \left\{ { 1, - 1} \right\}$ , 其中 ${v_i}$ 是类别标签; 设M为分类间距: 过各类样本中离分类平面最近且平行于分类面的平面之间距离; 设所求最优超平面方程为:

$ u \cdot w + s = 0 $

(7)

式中, $w$ 为超平面法向量, 决定了超平面的方向, $s$ 为位移量, 决定了超平面与原点的距离. 对式(7)进行归一化处理使得满足式(8):

${v_i}[(w \cdot {u_i}) + s] - 1 \ge 0$

(8)

若使M最大, 即求 ${\rm{||}}w{\rm{|}}{{\rm{|}}^2}$ 最小. 以式(9)为约束条件求 ${\rm{||}}w{\rm{|}}{{\rm{|}}^2}$ 最小是一个二次规划问题, 可以转为对偶问题求解.

$\sum\limits_{i = 1}^n {{v_i}{a_i} = 0,{a_i} \ge 0} $

(9)

以式(9)为约束条件, 对 ${a_i}$ 求解式(10)的最大值:

$f(u) = (w \cdot u) + s = \sum\limits_{{\rm{i = 1}}}^{\rm{n}} {{a_i}{v_i}({u_i} \cdot u) + s} $

(10)

其中, ${a_i}$ 为所求问题的Lagrange乘子. 则最优超平面分类问题可表示为:

$Q(a) = \sum\limits_{i = 1}^n {{a_i} - \frac{1}{2}\sum\limits_{i,j = 1}^n {{a_i}{a_j}{v_i}{v_j}({u_i} \cdot {u_j})} } $

(11)

由于基于RBF核函数的支持向量机识别精度高, 稳定性强^[13]. 因此文中采用基于RBF核函数 $K(u,v){\rm{ = exp}} \left[ {\dfrac{{ - ||u - v|{|^2}}}{{(2{\sigma ^2})}}} \right]$ 的支持向量机, 即令 $K({u_i},{u_j})$ = ${u_i} \cdot {u_j}$ , 则式(10)的分类函数可表示为:

$f(u) = (w \cdot u) + s = \sum\limits_{{\rm{i = 1}}}^{\rm{n}} {{a_i}{v_i}K({u_i},{u_j}) + s} $

(12)

若支持向量机需要识别k类, 采用1-v-r算法使用k个支持向量机独立训练, 每个分类器表示1个类别^[14]. 若k个分类的预测结果中存在多个二分类的正样本类, 将精确率作为分类的置信度, 精确率定义如下:

$PC = \frac{{TP}}{{TP + FP}}$

(13)

其中, TP是测试的样本预测为正样本, 并且测试的样本实际也为正样本的样本数; FP是测试的样本预测为正样本, 并且测试的样本实际为负样本的样本数. 最后将置信度最大的正样本类作为最终的预测类别:

$\arg \mathop {{\rm{max}}}\limits_{i = 1,2, \cdot \cdot \cdot ,k} {\rm{[}}P{C_i}{\rm{]}}$

(14)

其中, $P{C_i}$ 是第i类的精确率.

2.3 联合CNN-Softmax-SVM算法

联合CNN-Softmax-SVM算法是同时采用在原CNN模型的基础上添加了SVM分类过程和权重判定层, 其算法结构如图6所示.

将待识别轨迹特征输入卷积层、降采样层、全连接层得到一维形式的特征向量之后, 分别通过CNN网络的全连接层的Softmax层和用SVM分类函数代替CNN网络的全连接层的分类函数, 得到两种预分类结果, 将两种预分类结果输入权重判定层, 通过权重判定决定最终输出. 联合CNN-Softmax-SVM算法的实现步骤如算法1.

算法1.　联合CNN-Softmax-SVM算法

输入:

1) 待识别手势轨迹图 $\scriptstyle \bar M$ ;

2) 采用CNN-SVM训练样本后的每种类别识别正确率的平均值集合 $\scriptstyle {P_{\rm CNN - SVM}}{\rm{ = \{ }}{p_{\rm{1}}}({\bar x_1}),{p_{\rm{1}}}({\bar x_2}),{p_{\rm{1}}}({\bar x_3}), \cdots, {p_{\rm{1}}}({\bar x_n}){\rm{\} }}$ , 其中 $\scriptstyle{\bar x_i}$ 是采用CNN-SVM训练测试集的第i类, $\scriptstyle{p_{\rm{1}}}({\bar x_i})$ 是采用CNN-SVM训练样本后的第i类平均测试正确率;

3) 采用CNN-Softmax训练样本后的每种类别识别正确率的平均值集合 $\scriptstyle {P_{\rm CNN - Softmax }}{\rm{ = \{ }}{p_{\rm{2}}}({\bar y_1}),{p_{\rm{2}}}({\bar y_2}),{p_{\rm{2}}}({\bar y_3}), \cdots, {p_{\rm{2}}}({\bar y_n}){\rm{\} }}$ , 其中 $\scriptstyle {\bar y_i}$ 是采用CNN-Softmax训练测试集的第i类; $\scriptstyle{p_{\rm{2}}}({\bar y_i})$ 是采用CNN-Softmax训练样本后的第i类平均测试正确率;

输出:　识别类别 $\scriptstyle Class\_x$

1　 $\scriptstyle \bar M$ 经过卷积层、降采样层、全连接层得到一维特征向量 $\scriptstyle \vec m$ .

2　根据式(6)获取 $\scriptstyle \vec m$ 的类别y_CNN-Softmax; 根据式(14)获取 $\scriptstyle \vec m$ 的类别x_CNN-SVM.

3　获取CNN-SVM测试样本识别正确率的平均值 $\scriptstyle {\bar P_{\rm CNN - SVM}}{\rm{ = }}$ $\scriptstyle \frac{{\sum\limits_{i = 1}^n {{p_{\rm{1}}}({{\bar x}_i})} }}{n}$ ; 获取CNN-Softmax测试样本识别正确率的平均值 $\scriptstyle{\bar P_{\rm CNN - Softmax }}{\rm{ = }}$ $\scriptstyle \frac{{\sum\limits_{i = 1}^n {{p_2}({{\bar y}_i})} }}{n}$

4　if $\scriptstyle {y_{\rm CNN-Softmax }}$ = $\scriptstyle{x_{\rm CNN - SVM}}$ then

5　　 $\scriptstyle Class\_x$ = $\scriptstyle {y_{\rm CNN-Softmax }}$

6　else

7　　if $\scriptstyle{\bar P_{\rm CNN - SVM}} \geqslant {\bar P_{\rm CNN - Softmax }}$ then

8　　　if $\scriptstyle{p_{\rm{1}}}({x_{\rm CNN - SVM}}) \geqslant {p_{\rm{2}}}({y_{\rm CNN-Softmax }})$

9　　　　 $\scriptstyle Class\_x$ = $\scriptstyle {x_{\rm CNN - SVM}}$

10　　　else

11　　　　 $\scriptstyle Class\_x$ = $\scriptstyle{y_{\rm CNN-Softmax }}$

12　　　end if

13　　else

14　　　if $\scriptstyle{p_{\rm{1}}}({x_{\rm CNN - SVM}}) \leqslant {p_{\rm{2}}}({y_{\rm CNN-Softmax }})$

15　　　　 $\scriptstyle Class\_x{\rm{ = }}{y_{\rm CNN-Softmax }}$

16　　　else

17　　　　 $\scriptstyle Class\_x{\rm{ = }}{x_{\rm CNN - SVM}}$

18　　　end if

19　　end if

20　end if

3 实验分析

实验环境的硬件: intel(R) Core(TM) i5-9400 CPU @ 2.90 Hz 2.90 GHz; 内存: 8.00 GB; 系统类型: 64位操作系统, 基于x64的处理器; 便携式手贴纸: 贴纸形状为圆形, 贴纸直径为1 cm, 贴纸颜色采用蓝色(在HSV颜色空间下贴纸颜色范围: $100 \le H \le 124$ , $43 \le S \le 255$ , $46 \le V \le 255$ ); 摄像头: 罗技(Logitech) C270i IPTV高清网络摄像头720P.

实验从NIST数据集^[15]中整理出0-9数字字符样本图片各2000张用于改进卷积神经网络训练和测试, 实验样本数据的训练和预测都是仅在CPU下运行. 训练相关参数如表1.

CNN中所有网络各层的参数设置如表2所示, 其中F、S、P分别表示卷积池化窗的大小、窗口滑动的步长、图像的边界填充, ${K_f}$ 表示在当前网络层中卷积池化窗的个数, ${D_f}$ 表示当前网络层输出特征的维度.

CNN-Softmax和CNN-SVM在训练过程中的误差下降散点图如图7所示, 训练过程的精度折线图如图8所示. 其中CNN-Softmax的测试平均精确度为98.23%. 另一方面, CNN-SVM的测试平均精确度为98.04%.

实验邀请8名长期使用台式电脑的志愿者进行简单的互动, 每位志愿者每个数字字符累计实验15次. 其中手与摄像头距离阈值设置在0~60 cm范围内; 手指与摄像头中心之间角度阈值设置在0~18.3°范围内. 采用联合CNN-Softmax-SVM算法对动态手势进行识别, 识别结果如图9手势识别混淆矩阵所示, 识别混淆矩阵中第一横轴为识别出的结果, 第一纵轴为识别的类别.

由图9混淆矩阵可知, 本文方法对于动态手势轨迹具有较高的识别准确率. 在识别大部分数字字符上准确率可达到95%以上.

由于数字“0”和“6”、“2”和“3”、“4”和“6”、“5”和“6”、“5”和“8”在基于单目视觉下书写轨迹具有一定的相似性, 容易存在一定程度误判的情形. 单独采用CNN-Softmax算法在书写并识别“5”和“6”时识别率小于93%; 单独采用CNN-SVM算法在识别数字字符轨迹“2”、“3”、“4”时识别率小于93%; 采用本文提出的联合CNN-Softmax-SVM算法对0~9数字字符识别平均准确率能达到95%以上, 提高了相似字符识别的准确率.

表3给出了本文所提出的联合CNN-Softmax-SVM算法和单独采用CNN-Softmax和CNN-SVM算法的对比结果. 由表3可知, 尽管本文算法的平均识别时间略长, 但还是能满足实时性; 另外, 采用本文方法在识别率上相比其他几种方法有了较明显的提升.

4 结论与展望

基于单目视觉的特征轨迹提取方法, 有效地解决了复杂背景的干扰, 增强了手势数据的有效性并且能够适应大部分动态手势变换. 联合CNN-Softmax-SVM动态手势识别算法能够有效提取动态手势的轨迹特征, 在识别率上也有一定的提高. 但由于部分数字字符在基于单目视觉下书写轨迹具有相似性, 容易存在一定程度误判的情形. 在今后研究中应该进一步提高相似字符轨迹的识别率和识别时间. 除此之外, 本文研究是针对数字字符轨迹分类的手势识别, 也可以尝试对字母字符轨迹的手势识别进行实验研究, 以便更好地满足人机交互的需求.