2. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
3. 国网辽宁省电力有限公司, 沈阳 110168
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. State Grid Liaoning Electric Power Co. Ltd., Shenyang 110168, China
电力是国家发展的关键命脉, 是各行业及日常生活中至关重要的基础成分. 相关统计显示80%以上的停电事故都是因配电网故障导致的. 若在故障发生之前得到故障预警排查出故障所在位置并进行修复, 可以有效的减少停电故障的发生, 进而可以提升配电网的服务质量. 随着电网技术的不断提升相量测量装置和无线传感网络等电网基础设施的建设为电网提供了数据驱动的态势感知能力, 这为收集电网运行状态并使用这些状态进行相关研究提供了基础, 但是配电网故障影响因素众多, 并且结构复杂, 这都成为配电网故障预测的难点.
近年来相关的专家学者将研究方向集中在使用机器学习进行相关探索上. 郑晨玲[1]将贝叶斯估计法应用在故障定位上, 这种方法考虑到了配电网的内部结构, 具有一定的因果推理效果. 对本文预测算法结构的提出产生了很大的启发. 刘科研等[2]基于数据挖掘技术提出了一种风险预警方法, 核心思想是将每个站点的特征输入SVM中进行风险分类. 张稳等[3]针对天气因素使用ADABoost算法进行故障的预测. 以上方案都使用了经典的机器学习算法, 并且预测的对象主要集中在单一馈线上, 针对每条馈线建模预测每条馈线出现故障的概率, 并未考虑相连馈线间的互相影响. 本文结合图神经网络[4,5]的思想针对配电网实际结构的拓扑图进行建模, 融合了站点间流通的信息, 使得模型更加符合真实的环境. 文中提出的算法主要借鉴了Hamilton[6]提出的图卷积神经网络模型, 该模型可以支持多种聚合函数, 并且支持泛化到未知节点, 这样对算法的鲁棒性和泛化能力都有很大的提升[7].
本文使用东北地区某省会城市的配电网分布数据进行算法的仿真测试, 并与前人的方法进行了横向比较. 验证了本文提出的故障预测模型的准确性和鲁棒性, 对实际应用有一定的指导意义.
1 配电网结构分析配电网中主要的设备有变压器、多种传感器、隔离开关等, 这些设备的运行状态与整个配电网的运行状态息息相关. 设备的多样性, 以及天气等外界因素的影响使得配电网故障发生的原因比较难以确定, 这也为故障发生的预测带来了很大的困难. 研究发现配电网故障大多发生在馈线上, 所以本文建模的目标也延续与前文研究人员相同的方案, 预测的故障目标也是馈线是否会发生故障.
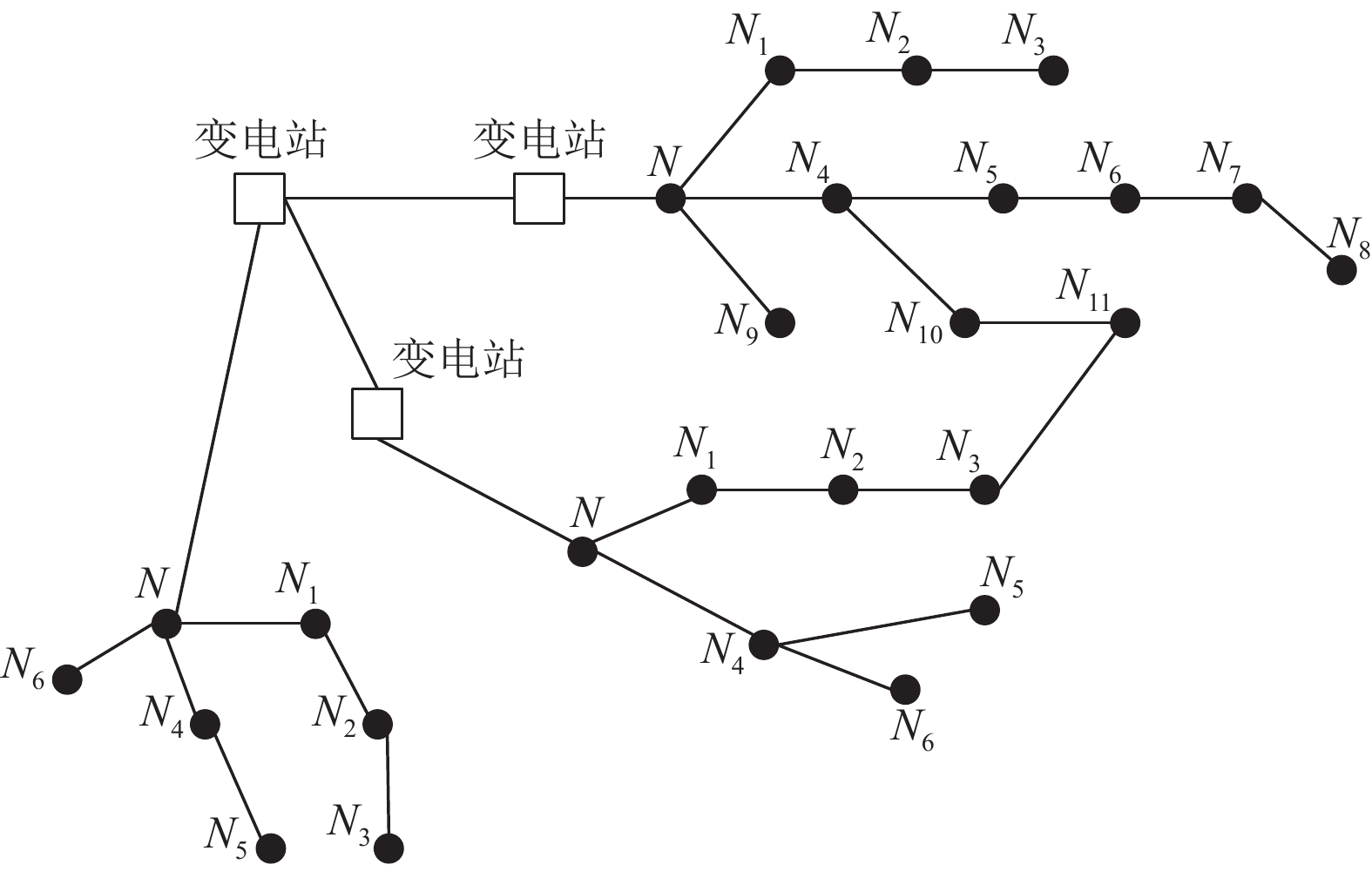
图1是选取的是某城区局部拓扑图. 图中正方形表示变电站. 黑色的圆点表示配电网节点, 节点是指从配电网干路出现分支的地方, 每个节点对应一条最小单位的馈线. 如果预测得出某一个节点将会出现故障, 易知代表与该节点连接的馈线会出现故障.
|
图 1 配电网局部拓扑图 |
2 算法模型 2.1 算法框架概述
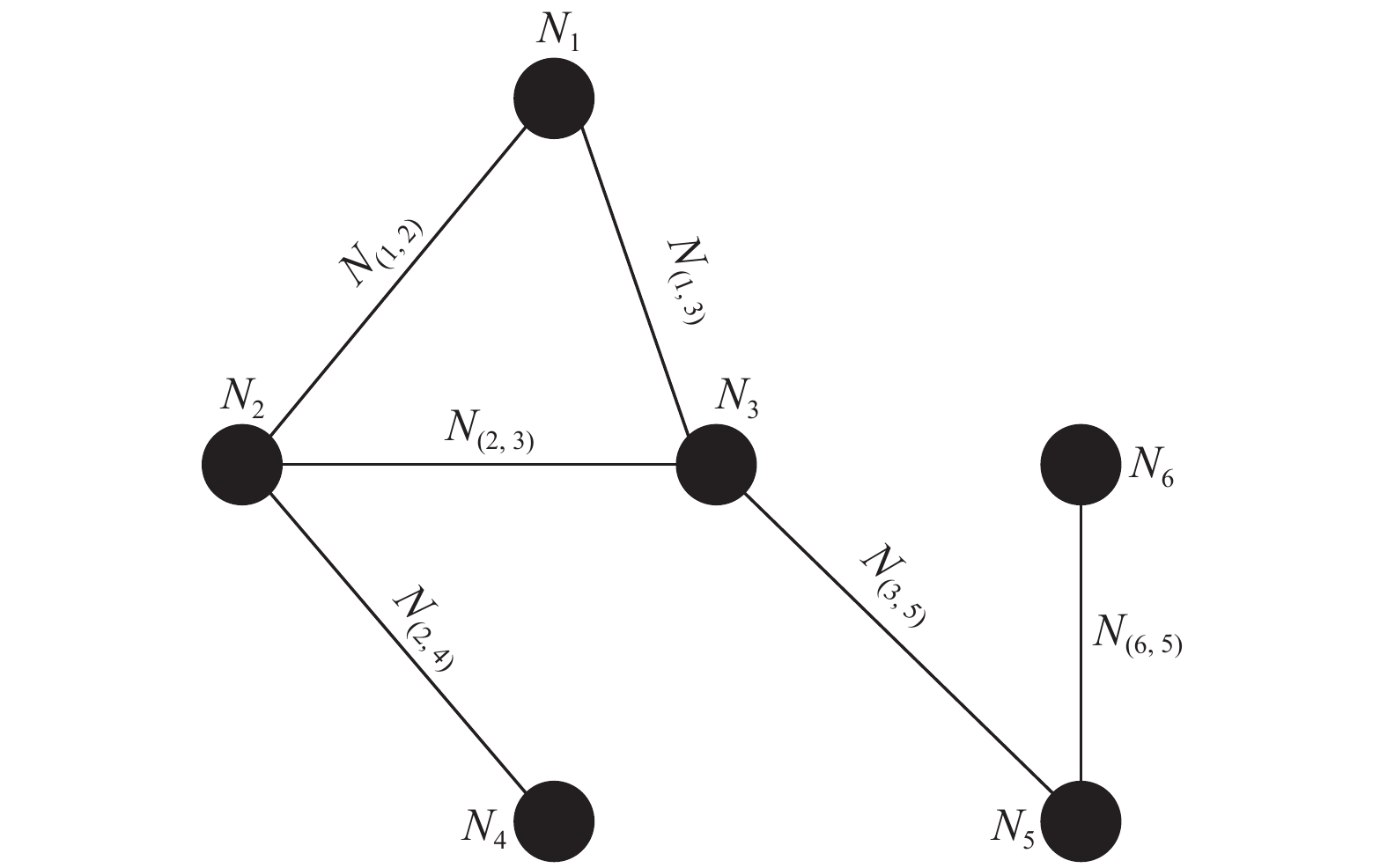
图神经网络是一种直接对图数据进行建模的神经网络模型, 本文主要参考了文献[6]提到的图神经网络框架, 并根据本文实际应用场景进行了细节上的微调. 为了更清晰的阐述算法本身, 我们设计了一个结构更简单的拓扑图, 如图2.
|
图 2 配电网简化拓扑图 |
观察图2中节点
| $\left\{\begin{array}{l} h_v^k = {f_v}({l_v},h_v^{k - 1},h_{ne[v]}^k) \\ {o_v} = {g_v}(h_v^k,{l_v}) \\ \end{array} \right.$ | (1) |
式(1)中,
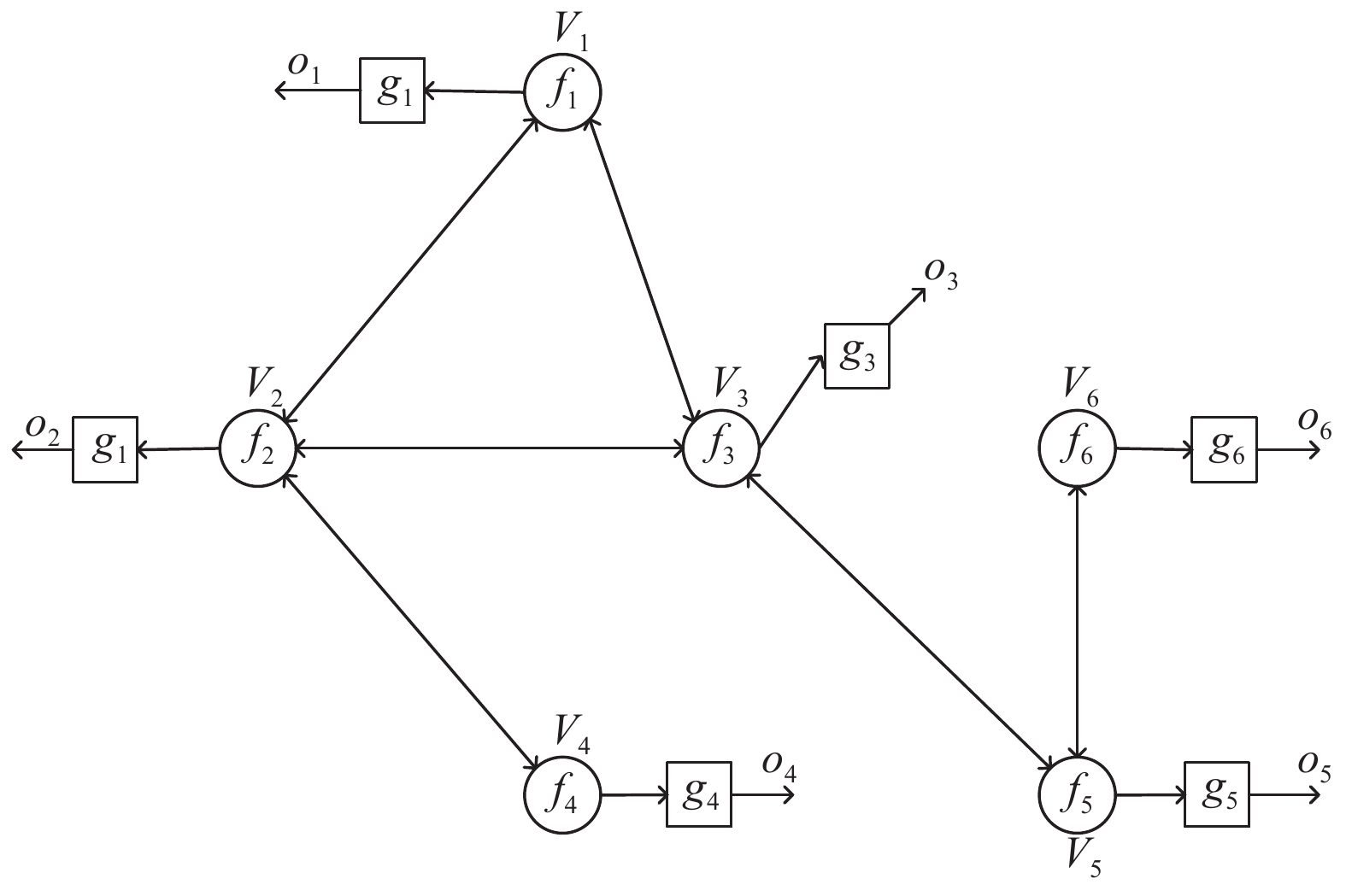
|
图 3 图模型计算结构 |
2.2 关键算法流程
常见的节点信息汇集方案有均值、卷积、序列等方法[12–14]. 本文通过在算法效率和精度方面的对比最终选定了如式(2)所示的均值法, 将目标节点和邻居节点的状态拼接起来并求平均值. 从应用场景角度来看, 本文参与求均值的节点是直接相邻的节点, 这些节点对目标节点影响最大. 但使用均值计算默认了节点间的权重相同, 而本文算法中节点类型恰好比较单一, 彼此对目标节点的影响趋势相近; 从数学角度来看, 均值方案计算简单且可导, 考虑到某些区域设备多导致运算量过大, 这个方法易于进行迭代优化, 特别是通过仿真实验验证均值方案计算效率最高并且精度与卷积方案差0.007, 位于第二位. 分析发现卷积方案本质上也是一种加权平均, 但是在执行速度上远远落后于普通平均, 综合考虑选定式(2)方案.
| $h_v^k \leftarrow \sigma (W_{agg}^k \cdot {{MEAN(\{ h}}_v^k{\rm{\} }} \cup {{\{ h}}_n^k{{,}}\forall {{n}} \in {{Ne[v]\} )}})$ | (2) |
节点信息汇集算法的完整流程如算法1所示. 算法1中
算法1. 节点信息聚合算法
输入: Graph
输出: 结果
1
2 for
3 for
4
5 end
6
7 end
8
外层循环
| ${o_v} = \sigma ({W_o} \times h_v^k)$ | (3) |
损失函数采用式(4)所示交叉熵损失的方式进行损失的计算. 因为输入
| $ L = {y_t}\log ({o_t}) + (1 - {y_t})\log (1 - {o_t}) $ | (4) |
形式比较简单易于计算, 并且不依赖Sigmoid函数的导数.
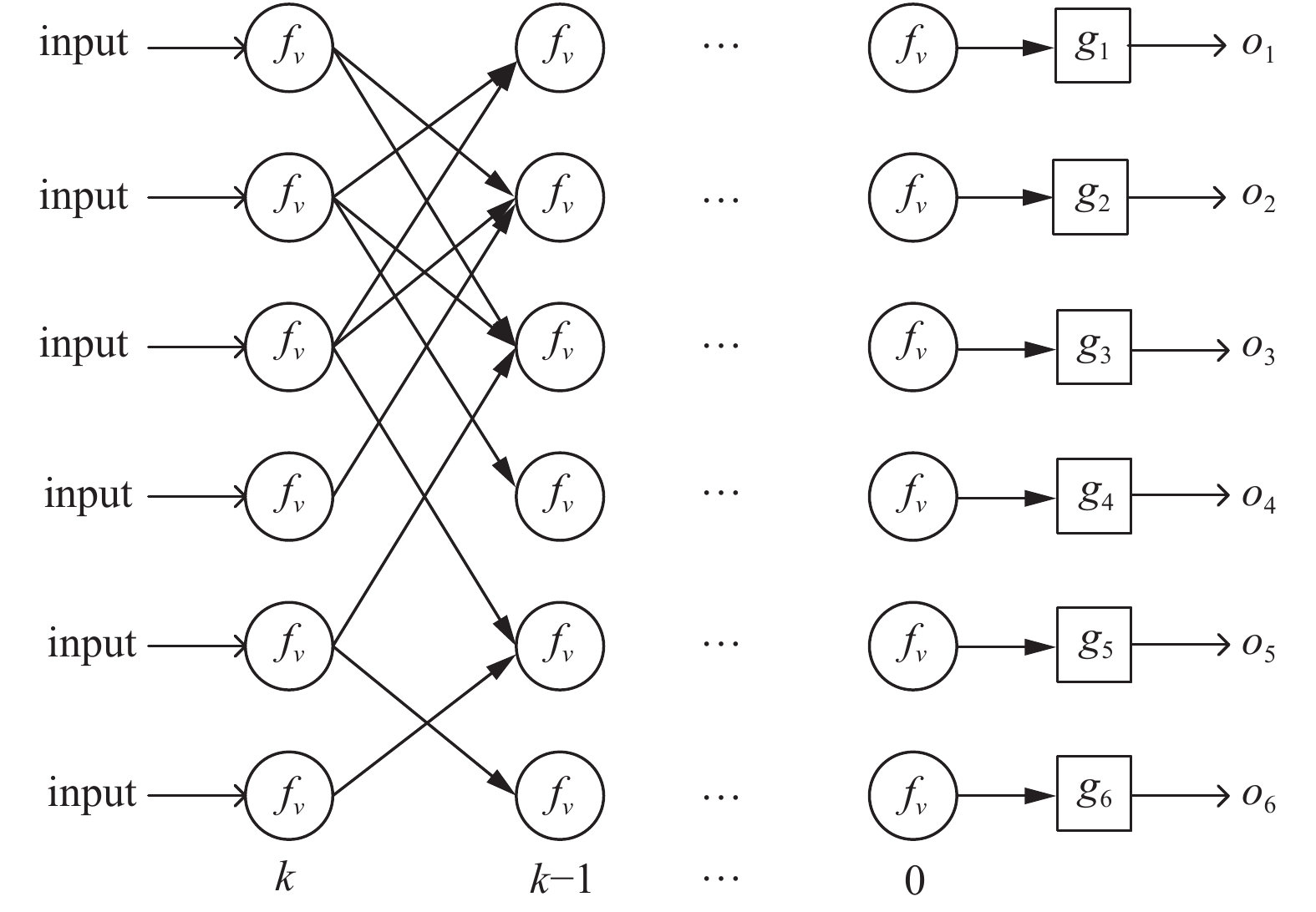
2.3 优化方法算法的优化采用常见的神经网络中前向传播和反向传播相同的思路[15]. 将图3展开成图4所示常见的神经网络结构, 容易发现图神经网络的层数由前文提到的k决定; 层与层间的连接关系由原图的连接关系决定.
|
图 4 网络展开图 |
整个模型的训练先进行从左向右的前向传播, 然后根据损失进行反向传播. 根据前向传播计算公式得到输出层计算梯度计算公式(5). 综上所述, 可以得到算法2所示整个模型的算法流程. 分析算法2, 第3行第1次迭代时, 每个节点编码了输入特征的信息, 第1次迭代时每个节点编码了本身以及直接相连节点的特征信息, 第2次迭代时每个节点的直接邻居节点包含了当前节点第2层节点的信息[16–18].
| $\left\{ \begin{aligned} \dfrac{{\partial L}}{{\partial {W_o}}}\;\;& = \left(\dfrac{{{y_t}}}{{{o_t}}} + \dfrac{{1 - {y_t}}}{{1 - {o_t}}}\right) \cdot \dfrac{{\partial {o_t}}}{{\partial {W_o}}}\\ & = \left(\dfrac{{{y_t}}}{{{o_t}}} \!+\! \dfrac{{1 - {y_t}}}{{1 - {o_t}}}\right)\! \cdot \! \sigma ({W_o}h_v^k\! +\! {b_o})(1 - \sigma ({W_o}h_v^k \!+ \!{b_o})) \cdot h_v^k \\ & = ({y_t} - {o_t}) \cdot h_v^k\\ \dfrac{{\partial L}}{{\partial {b_o}}} \;\;\; &= {y_t} - {o_t}\\ \dfrac{{\partial h_v^k}}{{\partial {W_{agg}}}}\! &= \sigma ({W_{agg}} \! \cdot \! h_v^{k \! - \! 1} \! + \! {b_{agg}}) \! \cdot \! (1 \! - \! \sigma ({W_{agg}} \! \cdot \! h_v^{k - 1} \! + \! {b_{agg}})) \! \cdot \! h_v^{k - 1}\\ \dfrac{{\partial h_v^k}}{{\partial {b_{agg}}}} &= \sigma ({W_{agg}} \cdot h_v^{k - 1} + {b_{agg}}) \cdot (1 - \sigma ({W_{agg}} \cdot h_v^{k - 1} + {b_{agg}})) \end{aligned}\right. $ | (5) |
算法2. 算法整体流程
输入: Graph
Different aggregator functions
for
End
return
For 2 to
仿真实验使用的数据来自东北地区某省会城市的配电网运行数据. 提取的影响因素根据文献[2]中提出的方案进行提取, 即分析了论文中提到的22个影响因素, 包括故障因素6个、自身因素3个、外部因素8个以及运行因素5个. 并计算特征值的权重. 本文的关注点在每条馈线的节点上, 而文献[2]在每条馈线上. 所以将有多条馈线发出的节点进行平均计算每个节点上的特征值表达.
根据以上方法本文共提取从2012年4月到2018年3月间某区的150条馈线数据作为训练样本, 2018年5月到2019年3月的数据作为测试样本, 预测用来验证模型的实际结果.
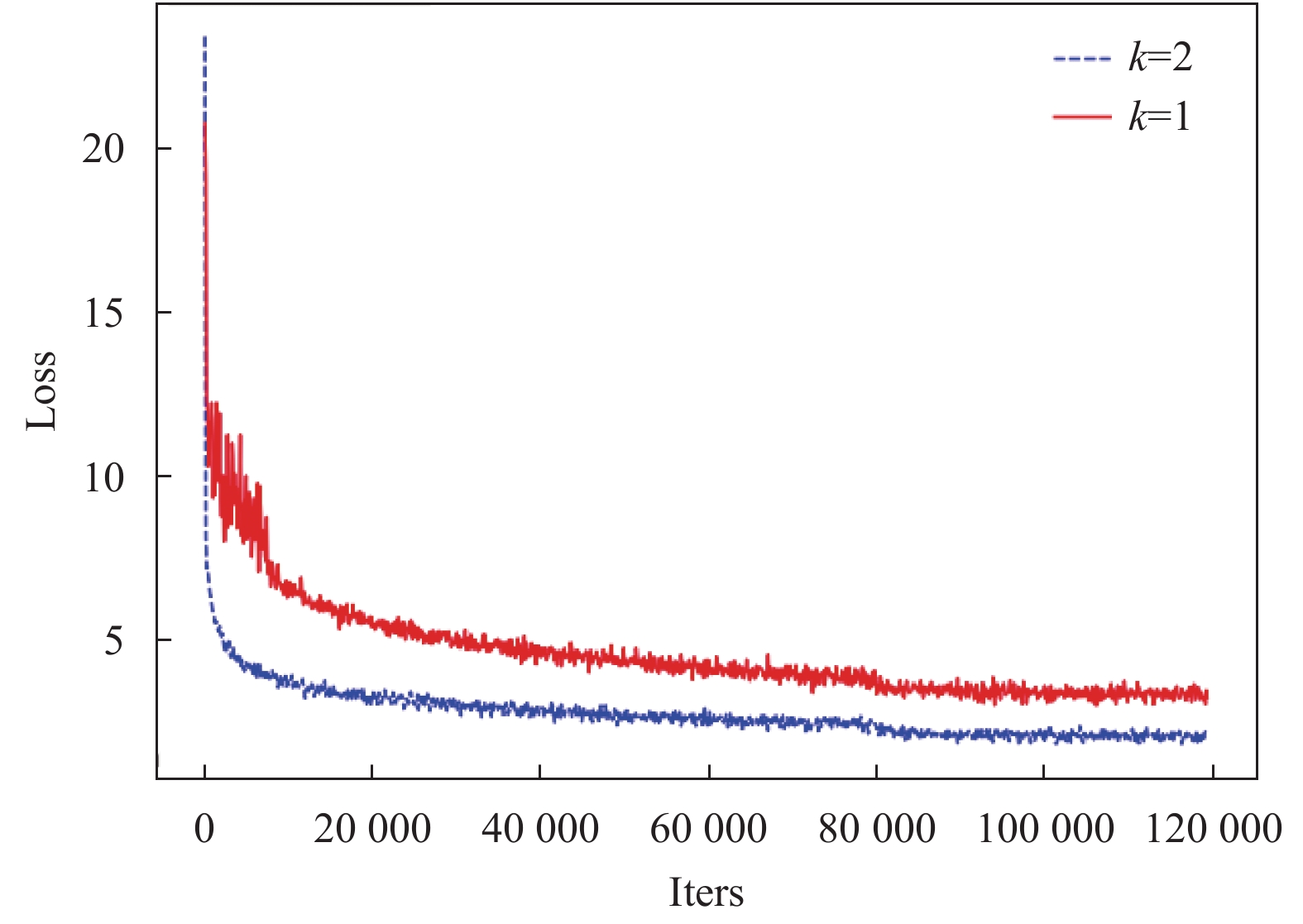
3.1 网络深度的取值与分析根据图5所示的训练曲线发现当深度为2时取得了更好的结果, 易知每个节点的信息都会通过迭代不断的向深层传递, 但是随着传递的层数越深信息强度也在不断的减弱. 本文实际应用场景中各节点分支最多为4个分支, 且选取的样本都在一个区域中在地理上比较接近, 节点与节点间样本特征上差别不大, 所以当传递的深度为3时出现了信息交叉出现进而影响到了模型的精度, 深度为1时模型的信息汇集程度不够loss比较高. 所以根据实际的测试结果选定了k值为2. 此外, 查阅相关论文得出, 在大型图网络中k的取值一般为3或者节点度的均值. 但结合本文来看, 最好方案还是结合实际的场景来分析设置.
|
图 5 不同k值的损失对比 |
3.2 模型对比
使用文中算法与之前研究人员使用的RBF-SVM[2]和ADABoost[3]算法进行对比分析. 数据采用的是上文提到的2018年6至2019年3月的数据, 并根据月份分别进行统计模型预测的准确率. 如表1所示, 前两种算法在模型的准确程度上取得了相对好的结果, 并且两个算法在8月份同时出现了预测准确率下降的现象. 分析发现因为东北地区8月份是最炎热的时候, 并且近年来的8月份非要比往年更加炎热, 导致出现了跟其他月份不同扰动因素, 进而模型预测的准确程度有所下降. 观察其他月份特别寒冷季节的月份, 模型预测都比较稳定.
观察本文提出的算法发现, 模型的鲁棒性和准确性都比较高. 这是因为模型是基于全局给出的一个结果. 最大程度上避免了随机因素扰动的干扰. 所以取得了在算法的准确上和算法的鲁棒性都取得了较好结果.
| 表 1 不同模型预测准确率对比结果(%) |
4 结论与展望
本文结合实际场景的特点和前人的研究成果, 提出了基于图神经网络的故障预测模型. 通过使用图神经网络进行配电网拓扑结构的真实建模, 有效的捕捉了各个节点间信息流通产生的相互影响. 并在小数据集上进行了测试, 测试的精度相比于前人在此领域上常用的方法上提高3.0%. 除此之外, 通过图神经网络对真实拓扑进行建模得到的模型鲁棒性更强. 但因为配电网结构复杂, 不同类型的节点众多, 本文选用的是配电网文本研究过程中常用的馈线为基本单位. 方法中还有许多不足之处, 后面还要考虑一下是否可以直接对不同的核心设备作为多类节点进行建模, 这样的建模方案才更加符合真实的配电网信息流动.
| [1] |
郑晨玲, 朱革兰. 基于贝叶斯估计的配电网智能分布式故障区段定位算法. 电网技术, 2020, 44(4): 1561-1567. |
| [2] |
刘科研, 吴心忠, 石琛, 等. 基于数据挖掘的配电网故障风险预警. 电力自动化设备, 2018, 38(5): 148-153. |
| [3] |
张稳, 盛万兴, 刘科研, 等. 计及天气因素相关性的配电网故障风险等级预测方法. 电网技术, 2018, 42(8): 2391-2398. |
| [4] |
Scarselli F, Gori M, Tsoi AC, et al. The graph neural network model. IEEE Transactions on Neural Networks, 2009, 20(1): 61-80. DOI:10.1109/TNN.2008.2005605 |
| [5] |
Zhou J, Cui GQ, Zhang ZY, et al. Graph neural networks: A review of methods and applications. arXiv: 1812.08434, 2018.
|
| [6] |
Hamilton WL, Ying R, Leskovec J. Inductive representation learning on large graphs. arXiv: 1706.02216, 2017.
|
| [7] |
Wu ZH, Pan SR, Chen FW, et al. A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems.
|
| [8] |
Cui P, Wang X, Pei J, et al. A survey on network embedding. IEEE Transactions on Knowledge and Data Engineering, 2019, 31(5): 833-852. DOI:10.1109/TKDE.2018.2849727 |
| [9] |
Hamilton WL, Ying R, Leskovec J. Representation learning on graphs: Methods and applications. IEEE Data Engineering Bulletin, 2017, 40(3): 52-74. |
| [10] |
Zhang DK, Yin J, Zhu XQ, et al. Network representation learning: A survey. IEEE transactions on Big Data, 2020, 6(1): 3-28. DOI:10.1109/TBDATA.2018.2850013 |
| [11] |
Cai HY, Zheng VW, Chang KCC. A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1616-1637. DOI:10.1109/TKDE.2018.2807452 |
| [12] |
Battaglia P, Pascanu R, Lai M, et al. Interaction networks for learning about objects, relations and physics. Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain. 2016. 4502–4510.
|
| [13] |
Atwood J, Towsley D. Diffusion-convolutional neural networks. Annual Conference on Neural Information Processing Systems 2016. Barcelona, Spain. 2016. 1993–2001.
|
| [14] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. Proceedings of the 5th International Conference on Learning Representations. Toulon, France. 2017.
|
| [15] |
Sanchez-Gonzalez A, Heess N, Springenberg JT, et al. Graph networks as learnable physics engines for inference and control. arXiv: 1806.01242, 2018.
|
| [16] |
Beck D, Haffari G, Cohn T. Graph-to-sequence learning using gated graph neural networks. Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics. Melbourne, Australia. 2018. 273–283.
|
| [17] |
Schlichtkrull M, Kipf TN, Bloem P, et al. Modeling relational data with graph convolutional networks. Proceedings of the 15th International Conference. Heraklion, Greece. 2018. 593–607.
|
| [18] |
Zhang ZW, Cui P, Zhu WW. Deep learning on graphs: A survey. arXiv: 1812.04202, 2018.
|
 2001, Vol. 29
2001, Vol. 29



