心血管相关疾病患病率逐年上升, 是世界公认的最常见的死因之一, 严重威胁人类健康[1]. 《世界卫生报告》[2]指出全球每年因心血管相关疾病引发的疾病及其并发症的死亡率已经超过了所有癌症死亡率之和. 其中, 冠心病的致死率很高, 诱发冠心病的主要因素是冠状动脉狭窄, 它会影响心脏供血, 严重会威胁生命[3], 因此研究血管狭窄程度可以辅助相关心血管疾病的诊断和治疗评估. 目前冠心病诊断的“金标准”[4]还是数字减影血管造影DSA (Digital Subtraction Angiography), 其他文章也有称之为常规冠脉造影CCA (Conventional Coronary Angiography)[5,6]. 采用这种介入方法可以最为直观地显示血管的形态和结构. DSA是一种用于介入放射学的透视技术, 可清晰地显示骨性或致密软组织环境中的血管. 成像时, 向血管中注入造影剂, 利用血管和其他组织部分对造影剂产生的差异来进行成像.
关于造影DSA图像中血管的分割, 相关的研究人员已有过研究和综述[7-9], 对血管的分割方法进行了较为详细的总结, 包含不同部位、不同类别的图像, 但针对某一种类别图像及特定部位的图像分割方法涉及较少. 针对心血管造影图像的分割, Tayebi等[10]将用于血管分割的模式识别方法分为6类: 多尺度方法、区域生长方法、匹配滤波法、数学形态学法、基于骨架的方法和基于脊的方法. 在其他造影图像中, 眼底荧光血管造影FFA (Fluorescein Fundus Angiography)图像相较于DSA图像而言, 背景里没有骨骼, 软组织, 造影剂等噪声因素, 其分离难度略低, 相关的研究也比较多, 也有相应的金标准数据集[11]. 很多在眼底血管分割中使用的方法可以在心血管的分割中使用, 但是由于心血管DSA影像自身的特点, 还需要对这些方法进行创新和调整.
本文在参考这些综述的基础上, 结合近几年的文章和分割方法, 专门针对心血管造影图像的分割方法进行了新的总结和, 将从3个不同的方面: 预处理、分割方法、评价标准来细分和总结, 技术框架如图1所示.

|
图 1 心血管造影图像分割技术框架 |
1 预处理
由于心血管造影图像的特殊性, 其图像内存在大量噪声, 图像模糊不均匀, 还存在其他组织或者骨头部分的影响. 因此图像预处理效果的好坏会直接影响到后续图像分割算法的效果, 图像的预处理一般有两个目的: 尽可能滤除图像中的无关干扰噪声, 对图像目标部分进行增强处理.
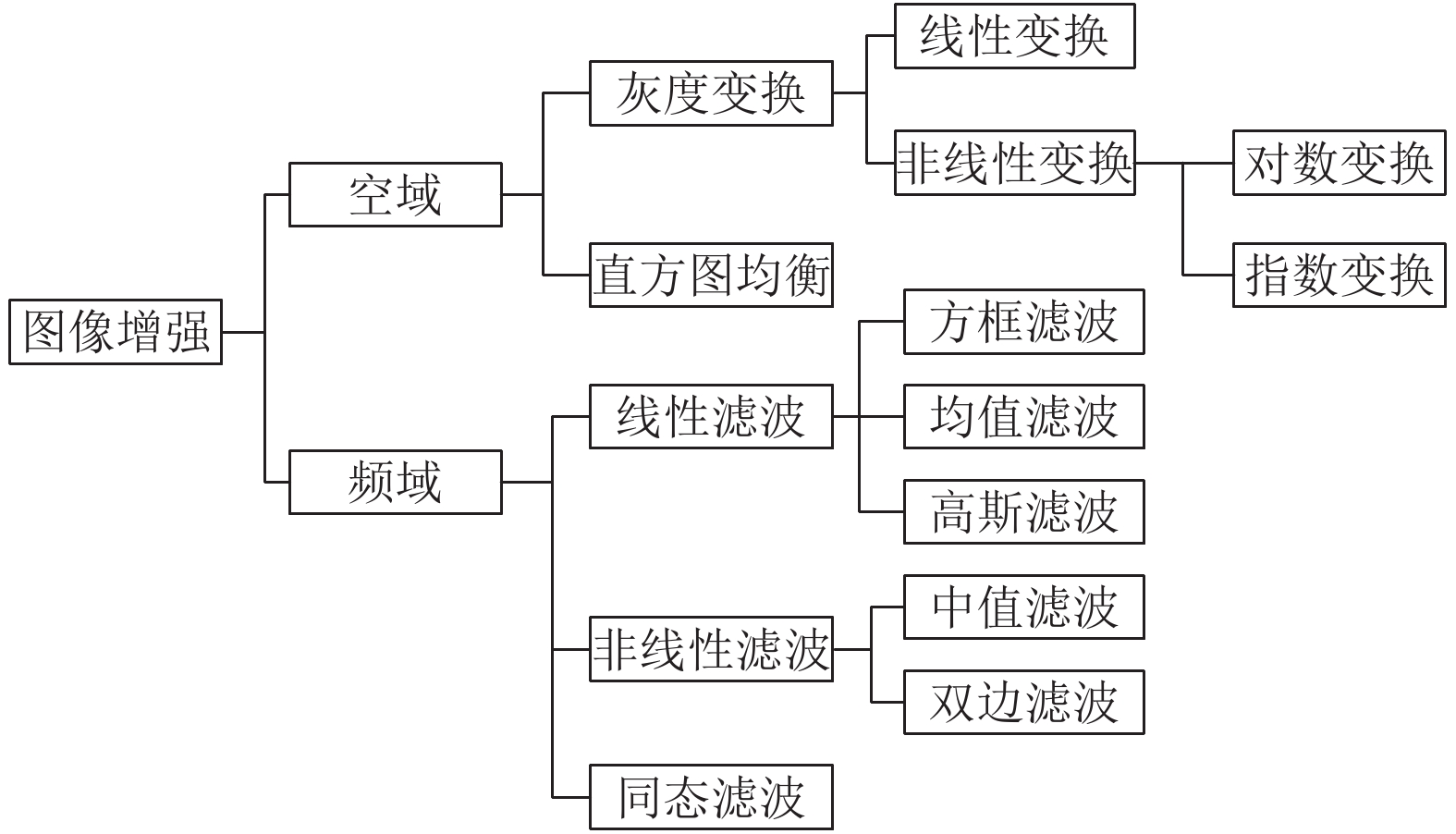
1.1 基于空域和频域的增强传统图像处理里面的增强方法大体上分为两大类: 基于空域和频域, 如图2所示. 基于空域的方法主要是对图像像素的空间域信息直接进行处理, 基于频域的方法首先将图像由空间域变换到频率域, 根据实际需要, 在频率域对图像进行处理, 最后再反变换回到空间域, 完成降噪或增强操作.
|
图 2 基于空域和频域的图像增强 |
灰度变换主要用于调整目标血管和背景造影剂之间的灰度差, 使得两者之间对比度更大, 以便于后续目标和背景的分离. 直方图均衡是一种基于图像的全局处理方法, 能在一定程度上提高图像整体对比度, 但是增强过程中会导致相邻灰度级合并, 进而使得图像中血管的细节消失. 针对这种不足Reza等[12]提出对比度受限的自适应直方图均衡方法CLAHE (Contrast Limit Adaptive Histogram Equalization), 但是这种方法在灰度级变化范围较小的图像的增强效果不明显, 在变化范围较大的区域可能会产生伪影. Zeng等[13]提出一种新的方法, 首先提取X射线图像的边缘信息, 然后根据边缘信息对图像划分区域, 分别对不同区域的灰度直方图赋予不同的权值, 以增强目标区域削弱背景区域. 这种方法对背景较为单一、结构较为简单的图像增强效果比较好, 对于结构比较复杂、对比度不高的图像效果不理想.
线性滤波和非线性滤波是图像处理领域历史悠久, 且操作十分便捷的去除图像中椒盐噪声及高斯分布噪声等的滤波方法. 在心血管分割中经常作为分割之前的前处理工作[14,15]. 陈楷丰[16]提出一种双边滤波器, 他将改进后的基于Hessian矩阵和基于高斯一阶导数的匹配滤波器结合起来对造影血管进行增强.
同态滤波是基于图像的频域, 将图像的亮度范围进行压缩同时增强图像对比度的方法. Oh等[17]提出一种基于形态学同态滤波的增强方法, 对图像中较暗的血管区域, 进行形态学滤波操作, 提取不同层级的频域高通分量和低通分量, 对其赋予不同的权值, 来增强目标的特征, 抑制背景部分.
1.2 基于多尺度方法的增强多尺度方法是使得图像在不同的图像分辨率下进行处理. 由于图像在选择不同分割尺度进行分割时, 分割的结果会不同. 若采用单一尺度进行分割, 分割的结果很难全面地反映分割对象的特征, 所以采用多个尺度综合多个不同分割尺度下的目标特征, 可以得到更佳的分割效果. 从低分辨率图像中提取大的主干结构, 诸如大血管的主要结构, 同时从高分辨率图像中提取其余精细的结构, 末梢处细小的血管部分. 多尺度方法在图像增强处理主要分为3种: 多尺度Hessian增强、多尺度形态学增强以及多尺度Gabor滤波器增强.
(1)多尺度Hessian增强
基于Hessian的多尺度增强方法由于能够获取血管的尺寸和方向信息而被广泛使用, 其中Hessian矩阵特征向量与血管结构有关. 传统的基于Hessian的增强方法[18]涉及多尺度高斯滤波器的多尺度卷积和Hessian特征值分析, 以像素为基础确定结构的局部形状(线状或斑点状).
在数学中, Hessian矩阵是函数的二阶偏导数的平方矩阵, 它是一种基于二阶导数的矩阵, 描述的是一个多变量函数的局部曲率[19], 根据这个矩阵两个特征值的特性, 可以进行线性结构的增强, 以及点状噪声点的去除. 根据线性尺度空间理论[20], 求微分的过程可以等价于原函数于高斯滤波器函数导数的卷积.
在进行二阶偏导求取之前, 需要进行高斯平滑操作, 所以高斯模板的方差大小对偏导数的大小会有影响, 求导窗口太大, 血管中细微的结构可能会丢失, 窗口太小, 可能会出现空洞的现象. 针对此, Frangi[18]提出使用多模板的方法, 对同一个点进行多种尺度的高斯模板进行卷积操作, 选择其中响应度最高的结果作为输出.
心血管造影图像中, 血管类似于管状, 响应值比较大, 背景的响应值比较小. 血管处的矩阵特征值是一大一小, 血管交叉处矩阵特征值两个都很大, 背景点处两个都较小, 令
| ${R_{{B}}} = \dfrac{{\left| {\lambda_1} \right|}}{{\left| {\lambda_2} \right|}}$ | (1) |
| $S{\rm{ = }}\sqrt {\lambda _{\rm{1}}^{\rm{2}}{\rm{ + }}\lambda _{\rm{2}}^{\rm{2}}} $ | (2) |
在当前的尺度下, 血管区域的响应函数如式(3)所示:
| ${\nu _0}\left( s \right) = \left\{ {\begin{array}{*{20}{c}} 0,&{{\rm if}\;\;\lambda_2 > 0} \\ {\exp \left( - \dfrac{{{R_B}^2}}{{2{\beta ^2}}}\right)\left(1 - \exp \left( - \dfrac{{{S^2}}}{{2{c^2}}}\right)\right)}&{} \end{array}} \right.$ | (3) |
其中,
这种方法的缺点在于它们有二阶导数的存在而对噪声高灵敏度, 由于角点的特征与类似斑点的结构很相似, 这个方法可能会抑制角点, 从而导致血管网络的不连续性. 为了克服上述问题, Truc等[21]采用方向滤波器组提取线状方向特征来增强血管, 以在嘈杂的环境中获得更有效地显示小而细的血管, 同时它能够避免角点抑制, 可以产生连续的血管树. 但是, 这种方法通常会导致强度不均匀性, 尤其是在血管连接区域. Xu等[22]进一步改进文献[21]的方法, 通过计算血管相似性度量作为增强方向图像重组中的权重, 以此来极大地保留尖锐血管边缘, 但由于强度的增强, 血管交叉处的信息可能会丢失. Zai等[23]采用引导滤波器作为预处理步骤, 可以抑制图像噪声, 平滑血管结构.
改进血管函数可以通过减少参数或者构造新的血管函数, 进而简化计算. Zhang等[24]简化了血管响应函数, 去除了参数c, 引入了新的
由于Hessian增强对于血管的增强效果良好, 后续许多研究者将此方法作为分割处理的一个步骤, 再结合其他不同的方法, 达到更好的分割效果.
(2)多尺度数学形态学增强
数学形态学操作[28]利用形态学算子提取图像中相应的结构, 可以进行图像的滤波、分割、分类等操作. 心血管造影图像中血管的灰度和背景的灰度不同, 可以通过数学形态学操作使得图像中亮的区域和暗的区域对比度更强.
文献[29-31]提出的多尺度形态学可以改善传统形态学变换的效果, 获取更多图像细节, 但是也可能在增强过程中引入新的噪声. Sun等[32]在使用模糊滤波和分水岭变换对血管进行分割之前采用多尺度数学形态学对血管树进行增强处理. Bai等[33]提出多尺度Top-Hat增强方法, 这个方法基于4种最基本的数学形态学运算, 每种图像运算都可以改变图像的对比度特性, 但不同大小的结构元对图像的效果不同, 从中选择最优特征进行增强操作. 这个方法在保留图像细节以及抑制图像噪声方面表现良好, 但是从整体上看, 整体对比度提升不明显. Fazlali等[34]采用Bai的方法在用超像素方法对血管进行分割之前采用多尺度Top-Hat的方法增强原始造影图像中血管部分和背景部分的对比度.
(3)多尺度Gabor滤波器增强
Gabor函数是图像处理中用于边缘提取的一种线性滤波器[35], 一个二维的Gabor滤波器是一个正弦平面波调制的高斯核函数. 在图像特征提取通常使用一组频率和方向都不同的Gabor函数. Cruz-Aceves等[36]使用多尺度Gabor滤波器对造影图像进行增强, 并和一些多尺度Hessian增强的方法进行了对比, 测试相同的图片时, 其提出的方法曲线下面积最大, 性能最佳.
图3分别列举了增强方法里面具有代表性的增强结果. 由于心血管造影血管图像的特殊性, 增强处理很难将血管完全分离出来, 只能将血管增强作为一个预处理步骤, 后续搭配不同的方法将血管整体分割出来. 表1总结了常用的分割预处理方法及其对应文献.

|
图 3 心血管造影图像增强效果 |
| 表 1 预处理方法及其参考文献 |
2 分割方法 2.1 传统分割方法
由于心血管造影图像中血管具有相对好的连通性、封闭性, 使得基于阈值的方法、区域生长的方法、基于统计学区域融合的方法以及基于匹配滤波的方法在分割中较为常见.
(1)阈值分割
其中基于阈值分割的方法由于其操作简单的特点, 很早就被用于目标分割, 它主要在目标于背景对比度较大的图像中发挥作用, 分为全局阈值法和局部阈值法. 全局阈值法对图像设定一个固定的阈值进行分割, 只能用于目标简单, 且图像较为简单的图像的分割. 局部阈值法首先通过一些局部统计量例如方差等来分别计算阈值[49]或者直接将图像划分为几个子图, 对每个子图进行阈值分割. 还有一种常用的最大类间方差法[50]是一种可以自适应确定阈值的分割方法. 对于心血管DSA图像, 其背景较为复杂, 分割难度较大, 不管是全局阈值法还是局部阈值法都不能找到一个合适的阈值进行分割, 所以阈值法一般作为分割过程中的一个处理步骤.
Khaleel等[51]针对心血管DSA造影图像, 首先进行高斯匹配滤波器操作, 再用阈值检测进行分割. Lian等[52]使用过基于迭代阈值的方法提取血管中的畸形部分, 他们首先将图像分割成数个子图像, 采用最大类间方差法将这些子图像分成两个不同的类别, 集合子图像间的灰度平均值和中位值不断迭代. Cruz-Aceves等[36]采用基于多目标的阈值方法对多尺度Gabor滤波器的幅度相应进行二值化来对血管进行分割, 从40张图像中提取阈值特征, 对40张测试图片进行测试, 同时将其结果与其他7种阈值分割方法进行对比.
(2)区域生长
基于区域生长的方法首先设定一个种子点, 不断遍历种子点像素的四邻域或者八邻域, 将和种子点相似的点归入同一个集合中, 再寻找集合中点的邻域相似点, 不断扩大区域, 直至完成分割, 这种方法对存在噪声以及对比度不均匀的像素区域及其敏感, 很易出现空洞或者过分割的情况[53,54]. 因此, 实际使用中, 区域生长的方法经常和其他分割方法结合使用.
由于血管的管状连通结构, 区域生长法十分适合对血管的连通区域进行提取. 为了避免各个血管段之间以及和背景之间造成的误分割, Sekiguchi等[55]在分割脑部MRA血管时提出了基于分支的区域增长方法, 对不同的分支采用不同的区域生长过程. Li等[56]提出一种结合灰度信息和空间信息的方法, 作为进行区域生长操作之前的条件判决, 提高了算法的健壮性. 但是, 在一些存在伪影, 或者对比度很低的血管区域, 区域生长的方法效果不佳, 很有可能导致误分割.
Wang等[38]首先进行多尺度Hessian增强, 基于多个种子点进行区域增长, 可以连接非连续的血管段, 比单个种子点增强方法效果更好. Kulathilake等[6]利用数学形态学方法和漫水填充方法实现区域增长操作, 最后从标记的血管结构中提取血管边缘. Asma等[40]在进行多尺度Hessian增强之后, 进行的区域生长操作也是基于不同尺度的, 设定的生长规则由于考虑了不同的尺度, 其结果对细小血管的分割结果更好. 庄宇等[42]在多尺度Hessian增强的特征图上采用种子点的自动选区方法分两个阶段进行区域增长来提取血管轮廓.
(3)统计学区域融合
基于统计学区域融合的方法最早由Nock等[57]在2004年提出, 此方法将图像中的像素点的灰度值看作一个统计学模型, 判断相邻像素点之间的相似性, 所有的像素点进行逐个判断, 是否进行区域合并, 最后根据统计学的分布特征来实现像素的融合.
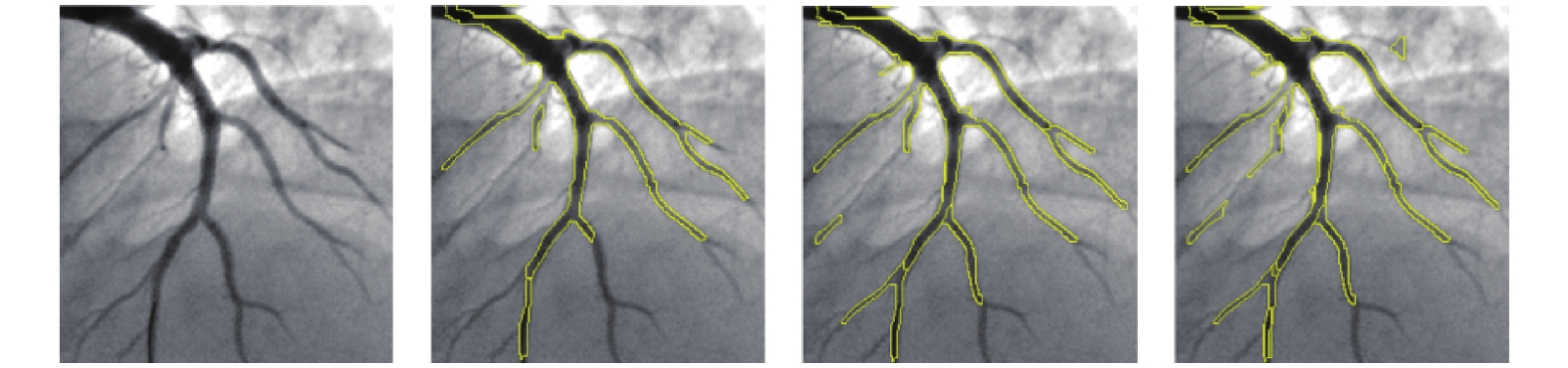
陈建辉等[14]在多尺度Hessian增强的基础上, 采用统计学区域融合的方法对目标血管区域进行融合, 得到分割好的血管, 再利用水平集方法对血管骨架进行提取, 进而评估血管狭窄程度. Wan等[43]对多尺度Hessian增强后的结果中目标部分的像素值采取4邻域统计学区域合并的方法, 用3套人工分割的结果分别和算法分割的结果进行平均绝对误差、豪斯多夫距离、DICE相似系数、敏感度、特异度、准确度的比较, 同时还对比了其他几种分割方法. 其分割的效果如图4所示.
|
图 4 统计学区域融合分割效果[43] |
(4)匹配滤波法
基于匹配滤波法是通过将图像与各种匹配滤波器进行卷积来完成目标提取的一种方法[58]. 因为造影图像中血管的大小尺度各异, 所以需要设计不同方向和尺度的多个过滤器进行卷积来提取血管轮廓. 在实际使用中, 匹配滤波器法通常与其他图像处理算法一起使用, 例如阈值分割和连通域分析.
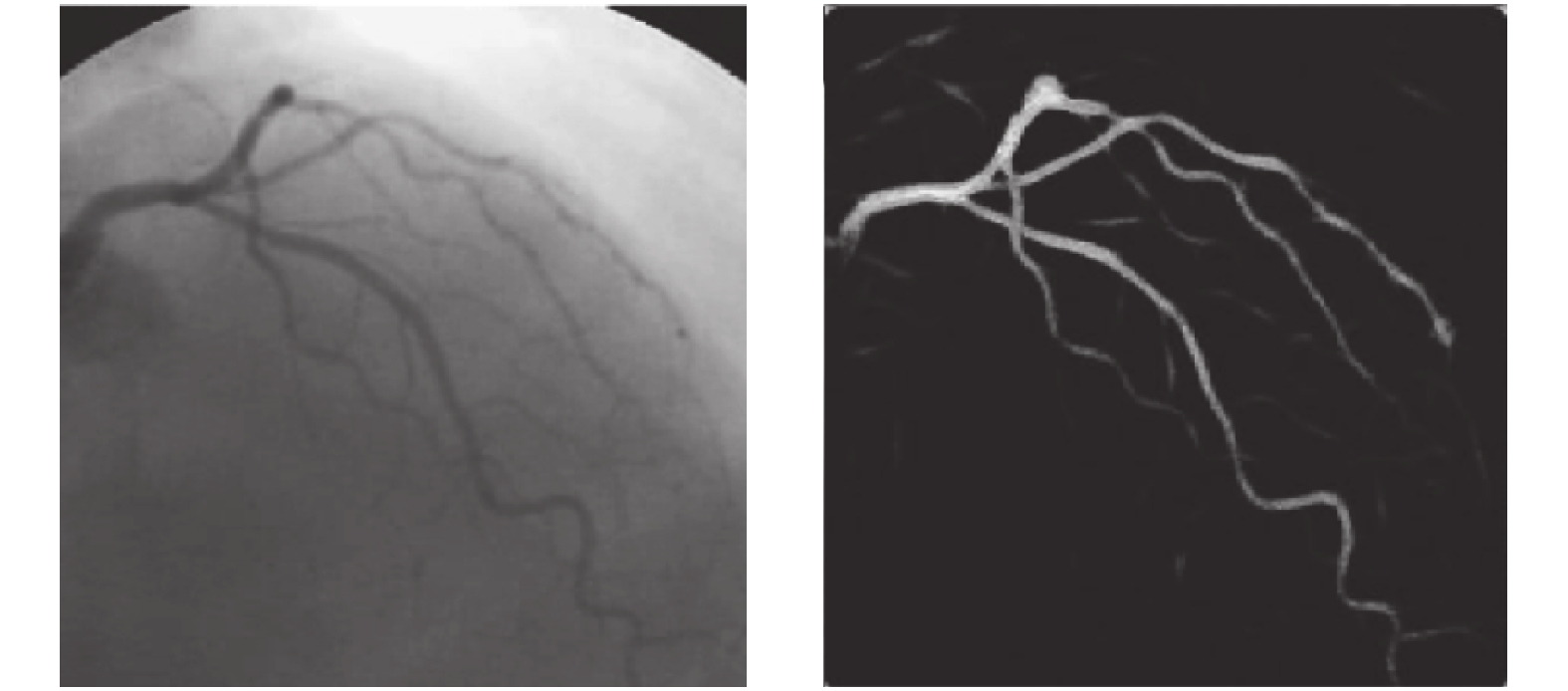
这个方法主要是基于信号处理中的匹配滤波器, 当匹配滤波器性能和信号的特性取得一致时, 可以使得滤波器输出的信噪比最大, 根据此来进行匹配滤波器的设计. Khaleel等[51]设计的一种基于高斯匹配滤波器, 首先进行高斯匹配滤波再进行阈值检测进行分割. Cruz-Aceves等[59]为了优化基于高斯匹配滤波的分割方法, 比较了4种仿生算法, 最后对比结果表明差分进化算法的分割效果最佳. 后续他们又提出一种基于神经网络的多尺度高斯匹配滤波器[60], 改善了之前只有单一尺度检验血管的缺陷, 其效果如图5所示.
|
图 5 匹配滤波法分割效果[60] |
2.2 可形变模型
可形变模型首先将待分割的血管结构(一般指曲面或者曲线)定义为一个初始血管模型, 这个模型受到内力和外力的作用会逐渐发生形变, 当这个形变逐渐接近血管轮廓时, 就可以将血管分割结构分割出来. 一般血管模型受到的外力指图像的特征, 比如像素灰度值, 梯度等, 受到的内力一般只曲线自身的形态特征, 比如曲率、弧长等. 根据形变模型的分割方法可以分为基于边界和基于区域的方法.
(1)基于边界
基于边界的方法中, 蛇线模型[61]以及水平集方法[62]在血管分割中的应用较为广泛. 其主要原理是利用梯度矢量流(Gradient Vector Flow, GVF)[63]以及区域内外的内外力约束指导模型向边界移动, 实现分割.
Devi等[64]为活动模型提供了一种新的外力, 解决了很多snake模型无法提供更好捕获范围和进化停止机制的问题. Brieva等[65]提出一种基于Mumford-Shah函数的方法, 使得在分割复杂冠脉血管树时效果更好. Sum等[66]提出基于水平集的动态轮廓分割方法, 通过引入区域的统计参数和局部的图像差异可以解决灰度强度不均匀的问题. Khokhar等[67]在标准水平集函数中引入了曲率特征能量函数, 提高了曲线演化的能力, 且所需迭代次数少.
水平集分割方法对复杂的图像容易收敛于能量极值, 而且计算量较大. 在背景复杂的图像中, 容易收到噪声和伪影的影响, 造成误分割.
(2)基于区域
基于区域的形变模型方法主要通过前景和背景的区域统计信息来指导血管模型的轮廓演变, 图像在分割时被分为目标前景区域和背景区域, 根据边界、前景和背景的统计特征定义一个图像能量函数, 当模型发生演变时, 能量会随之发生变化, 当总能量最小时, 前景区域即为目标区域. 因此能量函数的定义对分割精度影响很大. Wang等[68]利用基于区域能量模型的方法, 提取血管部分以及分割脑部MRA图像. Dehkordi等[45]提出的局部特征适应LFF模型可以提取强度不均匀造影图像中的血管树. Sun等[69]提出的局部形态学适应LMF模型能够处理强度不均匀的血管图像, 这种方法鲁棒性较强, 无需前后处理.
基于可形变模型的方法设置的能量泛函只依赖于曲线参数的选择, 而且受初始轮廓影响较大, 对于复杂的曲线拓扑结构处理起来比较困难, 这是可形变模型法在血管分割泛化中受到限制的原因.
2.3 轨迹追踪法基于追踪的分割方法是一种模板匹配方法, 应用于具有连续结构的图像分割. 首先指定一个特定结构的模型, 通过计算模型自身和周围的局部特征来确定下一个模型的位置和方向, 利用不同的图像特征例如梯度来不断评估图像和设定模型之间的匹配程度, 不断修正和调整方向来获得与目标最为匹配的血管模型. 这个方法多用于3D模型的分割. 在2D图像的分割过程中, 首先需要给定一个或者多个种子点, 种子点可以通过手动标记或者血管增强的方法得到, 再根据局部算子对中心线或者血管边界进行追踪. 追踪方法可以分为基于模型的方法和最小成本路径法.
基于模型的方法, 主要的缺点是如果遇到血管强度不均匀或者噪声很明显以及病变区域, 追踪会提前终止. Zhou等[26]采用一种基于多特征的模糊识别方法来指导概率跟踪算子沿着血管树的跟踪, 在跟踪过程的同时实现对血管轴线和直径的测量. 后续他将血管结构识别算子和血管跟踪算子引入血管的模糊推理识别中实现对血管分叉等的跟踪[44].
基于最小成本路径的方法一般是用于提取血管中心线, 为后续狭窄程度评估或者三维重建奠定基础. 文献[70,71]里提到了利用空间中中心线的位置以及图像灰度特征来进行血管表面的提取, 其优点在于搜索速度快, 避免出现局部最小值的情况. 将最小成本路径方法和区域增长方法结合还可以克服血管交叉处的影响, 提取较为细小的血管[54].
轨迹追踪法需要在最初人工选定起点和终点, 是一种半自动化的分割方法, 必须依赖于相关人员的判断和操作. 如何使其自动化以及更加高效在检测血管边界和中心线的过程中有重大意义.
2.4 图论基于图论的方法是将整个图像映射为图的一种方法. 其中一种经典的图割分割算法通过求解能量函数最小化问题进行分割. Hernández-Vela等[72]在提取中心线及进行半径测量时利用图割的能量函数进行全局优化, 可以实现血管的自动分割. 这种方法十分便捷, 但是在计算时时间复杂度和空间复杂度较高.
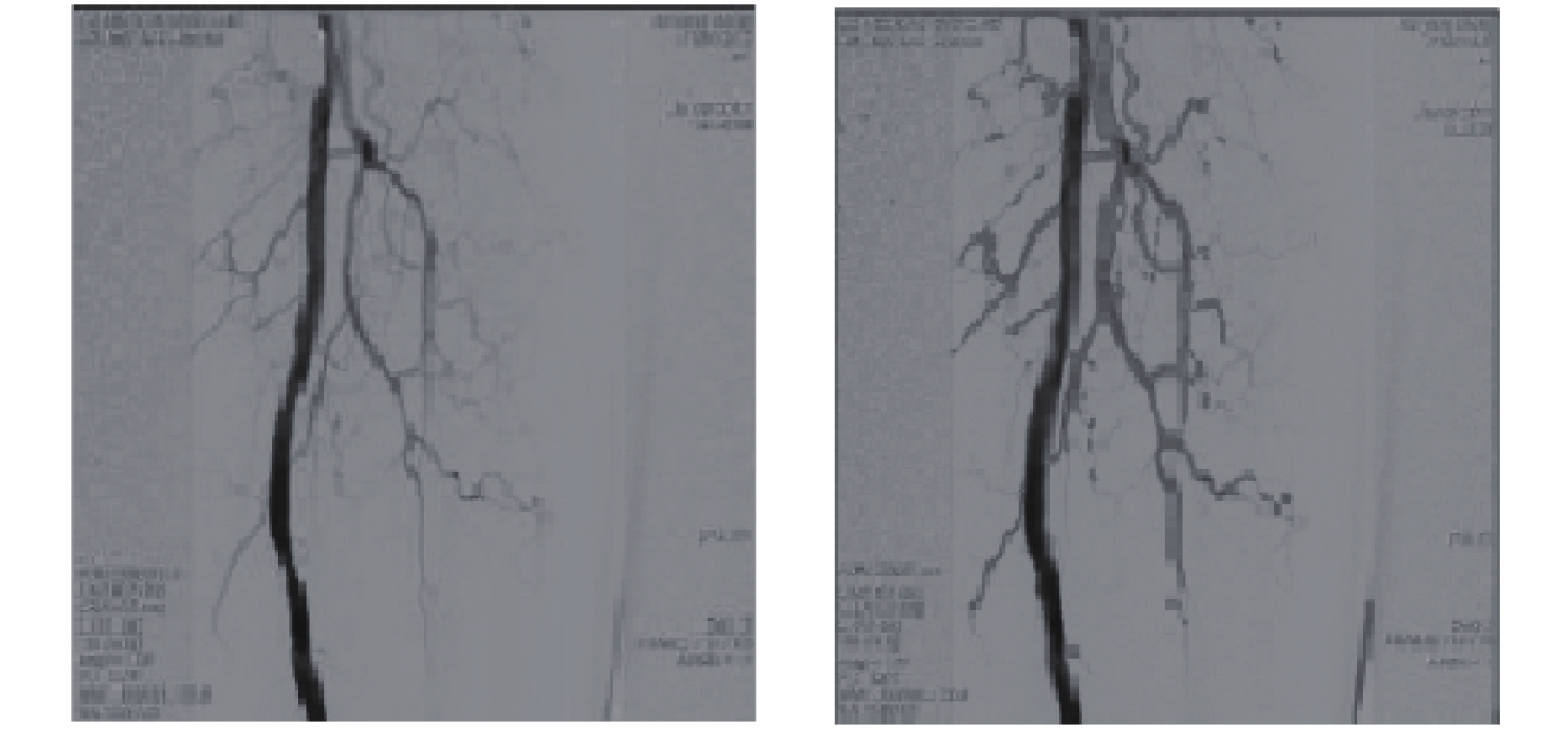
另一种常用的方法是随机游走算法, 它将图像看作包含固定顶点和边的连通带权无向图, 首先人工指定目标初始种子点以及背景种子点, 然后根据各个顶点到这两个种子点的概率判断种子点在随机漫步时的归属类. M’hiri等[46]提出的血管随机游走方法, 将Hessian增强和随机游走相结合, 需要人工选定种子点进行分割. 王光磊等[37]采用一种新的自适应阈值分割法进行预分割, 再通过结合数学形态学为随机游走算法提供种子点, 可以实现自动化分割. 其分割结果如图6所示.
|
图 6 随机游走算法分割效果[37] |
2.5 机器学习
基于机器学习的方法是将分割问题转化为一个分类问题, 是近几年应用最多的一种分割方法. 不断有新的机器学习方法和深度学习方法应用到医学图像的处理当中来[73,74]. 早在1995年, Nekovei等[75]就采用BP神经网络来对血管结构进行检测, 将预先标记好的造影图像送入神经网络中进行训练. 近几年卷积神经网络CNN在的一些图像分割处理当中取得不错的效果[76]. 在所有的深度学习网络结构当中, U-Net是目前在二维医学图像分割领域中应用最为广泛的一种网络结构[77]. 它由Ronneberger等[78]在FCN的基础上提出, 主要特点是网络呈现“U”型, 其上采样层和下采样层数量相等.
基于机器学习的方法主要分为两类, 一类是需要建立分割标准的有监督方法, 这个分割标准(Ground-truth)需要由专家手工标记得到, 由于血管数目繁多, 手工标记比较耗费时间, 用于有监督方法的机器学习要求将Ground-truth组成训练集, 从训练集数据中运用相关机器学习方法推断出一种模型, 利用这个模型对未分割的图像进行分割. 近几年使用很多的CNN和U-Net网络都属于这种有监督方法.
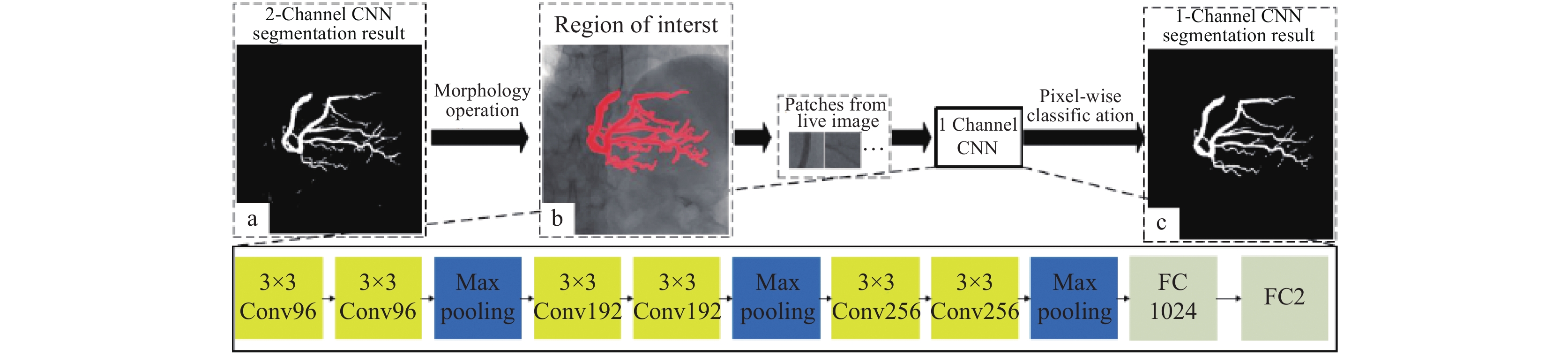
Nasr-Esfahani等[47]从每个512×512进行顶帽操作后的造影图像中提取40000个图像块, 一半来自血管, 一半来自背景区域, 将这些图像块输入CNN网络, 进而通过判断是血管还是背景来对血管实现分割. 后续他们将全局的信息和局部信息结合起来[48], 并且引入了canny边缘检测器来进行训练, 得到的分割效果更好. Yang等[79]在CNN单通道的方法上加入了图像掩模通道, 用双通道的处理办法在去除导管区域和伪影方面效果更高, 如图7所示. Jo等[80]提出一种选择性特征映射的方法, 用以分割心血管图像中的左前降主干. Zhao等[81]在imagenet基础上建立一个初始神经网络, 再将其运用到针对半监督视频对象分割问题的单镜头视频对象分割[82]的CNN框架上.
|
图 7 双通道卷积神经网络分割[79] |
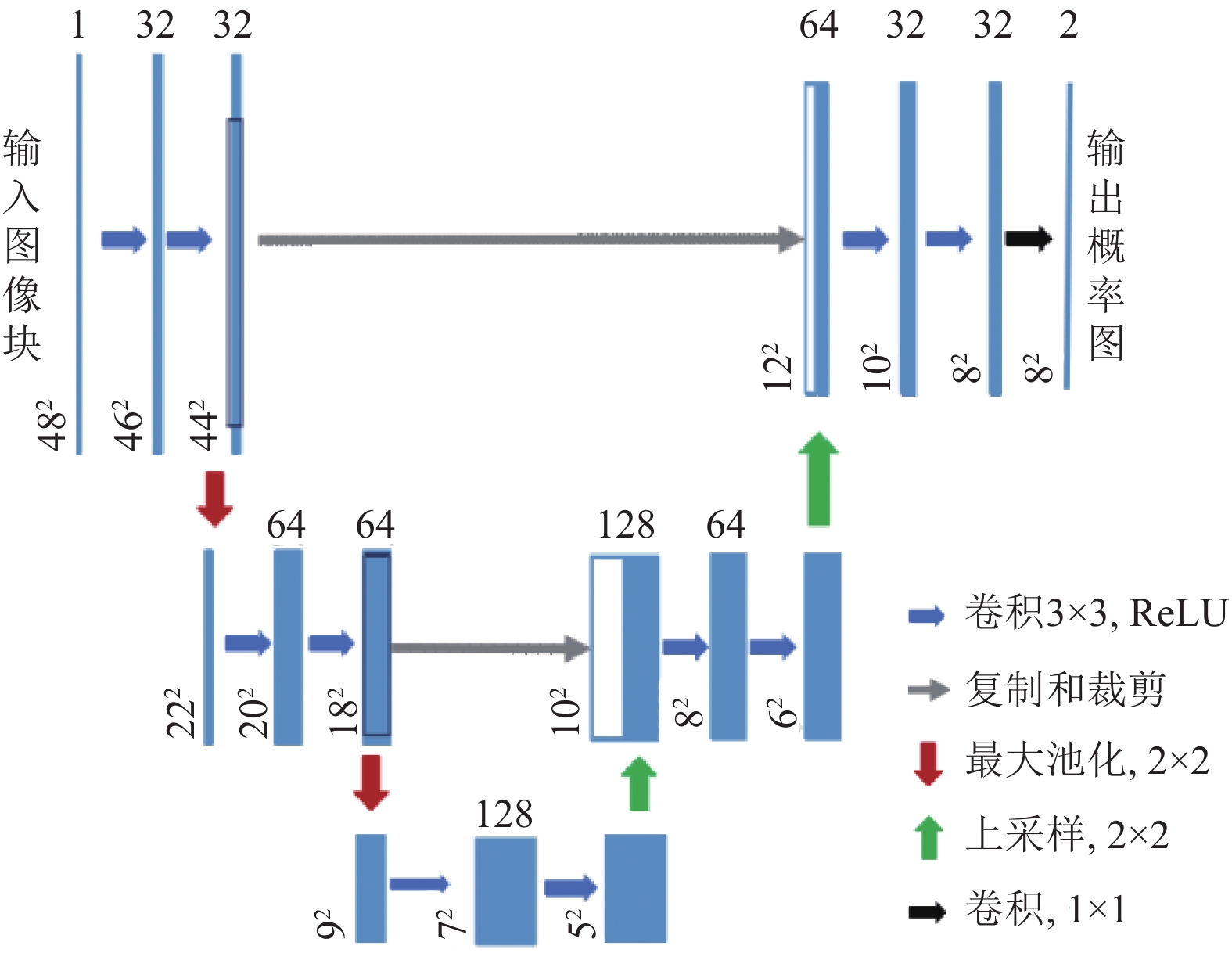
李裕[5]使用多尺度Top-Hat算法增强血管的细节特征, 使用修改后的U-Net模型对心血管造影图像进行分割, 如图8所示. 杨少戈[83]获取了大量不同体位不同病变情形的冠脉造影图像, 对其进行粗标注和精细标注, 使用PSPNet网络分别训练不同体位下的冠脉造影图像, 对其进行分割. Yang等[84]提出一种基于U-Net架构的全卷积网络结构, 在DICE系数中加入了假阳性和假阴性的惩罚项, 引入了一种新的损失函数PGD对主血管部分进行分割. Au等[85]第一次采用深度学习来全自动实现评价血管狭窄程度的QCA[86]过程, 主要分为狭窄部位的定位, 血管的分割, 狭窄程度三个方面. Fan等[87]将造影前的图像掩模信息和造影后的血管信息都用作多通道的输入以增强血管的结构信息, 还对掩模图像和血管图像进行了匹配, 以获得更加精确的对准效果. Jun等[88]为了克服U-Net在编码和解码块之间只有一组级联层的限制, 引入了T-Net一种全新的网络, 在编码器处理期时适当安排池化层和上采用层, 使得预测的掩模更加精准.
|
图 8 改进U-Net网络分割[5] |
另一类是无须制作人工标记标签的无监督方法, 直接从输入数据中寻找隐藏规律, 其中聚类算法使用最为广泛. Plourde等[39]采用机器学习的方法来改善经过多尺度Hessian增强处理之后的造影图像, 使用基于轮廓的算法进行特征提取, 再利用支持向量机SVM对其进行分类. 这个方法可以提升多尺度Hessian增强的效果. Lassó等[89]利用支持向量机SVM去学习造影剂注入后引起的图像灰度演变的特征, 根据演变特征, 设计增强方法, 进而更好地抑制噪声部分.
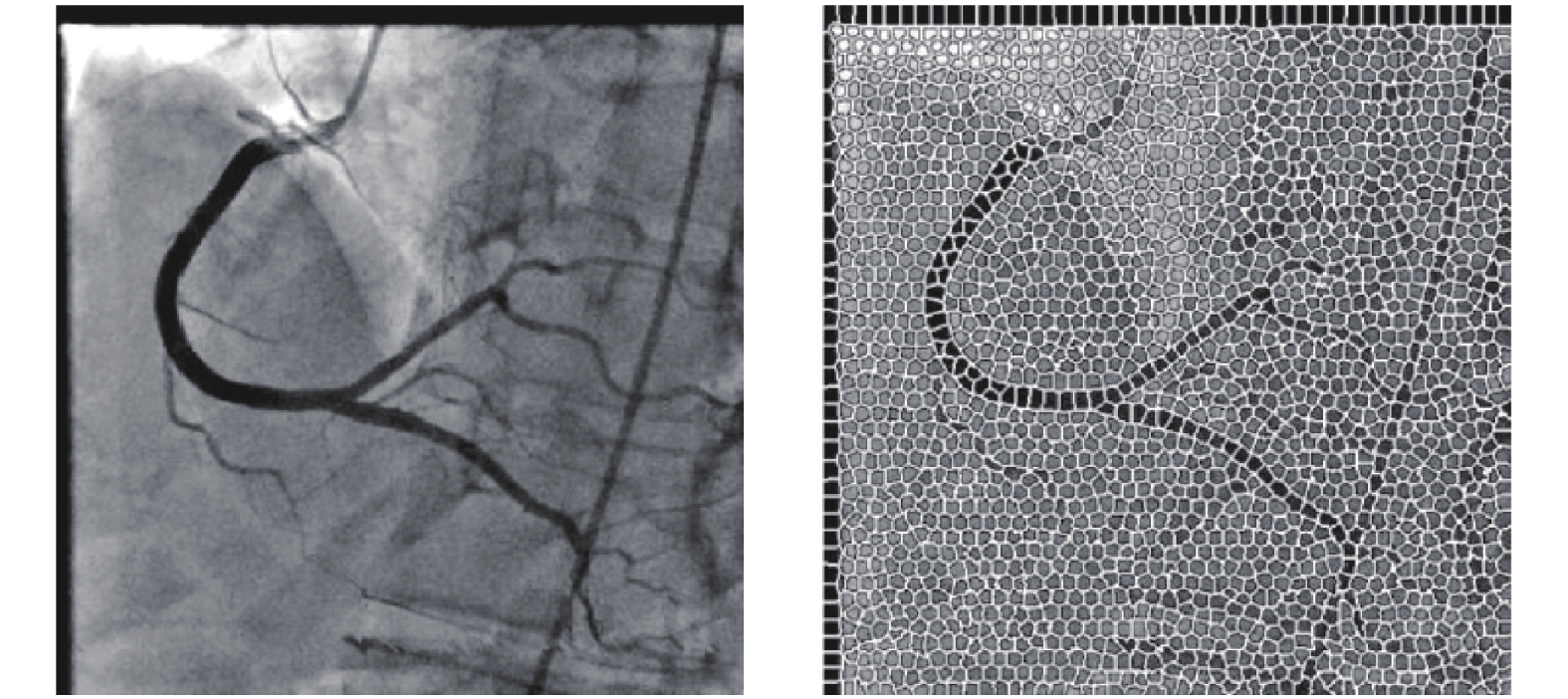
2.6 超像素方法超像素是指具有相似纹理、颜色、亮度等特征的相邻像素构成的具有视觉意义的像素块, 通常是不规则的. 与像素相比, 提取超像素更加有利于提取图像的局部特征, 且计算复杂度更低. 目前关于基于超像素分割的算法主要分为两类, 一类是基于图论的方法, 一类是基于梯度下降的方法. Achanta等[90]提出的SLIC算法将彩色图像转换为5维特征向量, 再构造度量标准对像素进行局部聚类, 此算法运算速度块, 生成的超像素块较为均匀. Fazlali等[34]在对原始造影图像进行多尺度Top-Hat变换和多尺度Hessian增强操作后, 利用多尺度分割方法对血管进行初始分割, 然后计算每个超像素块的血管概率, 和设定的阈值相比较, 进而区分出血管部分和背景部分, 实现分割, 效果图如图9所示.
|
图 9 基于超像素方法的分割效果[34] |
由于目前没有公开的金标准数据集, 不同研究人员采用的图片数据不同, 评价标准也不相同, 其研究成果很难拿来比较. 表2总结了常用的分割方法及其对应文献, 还包括检测分割算法时所测试的图片数量及使用的评价标准.
3 评价标准对于血管分割的评价指标, 金标准还是由临床专家医生手动分割的图片. 由于在专家们进行手动分割时会产生人工误差及因主观性判断导致的不一致, 因此需要提出使用不同的策略来对金标准进行选定, 即在血管分割中选择大部分专家都认同的血管段作为分割金标准, 或者建立可信度列表, 在出现分割争议时, 根据可信度列表排名进行评判[83]. 但是以上方法, 不能够引入分割结构的先验信息, 并且不能够评估局部的分割效果. 为了解决这个问题, 引入同步真实性能水平估计STAPLE (Simultaneous Truth And Performance Level Estimation)算法[91], 该方法结合先验模型对被分割结构的空间分布进行约束, 再对每个不一致的分割结果的性能进行度量, 最后利用标签融合方法将各个专家的分割结果以最佳的方式结合起来.
| 表 2 分割方法及其对应文献 |
在评估分割算法的性能时, 通常采用真阳性TP (True Positive), 真阴性TN (True Negative), 假阴性FN (False Negative)和假阳性假正例FP (False Positive). 4种数据的参数表[92]如表3所示. 分析这4个数据又可以产生不同的评价指标, 例如灵敏度, 特异度, 准确率(即查准率), 召回率(即查全率), 阴性预测值PPV, 阳性预测值NPV, 边界误差. 除此之外, 还有平均绝对误差MAD(Mean Absolute Difference)[93]、豪斯多夫距离HD[94]、DICE相似系数DSC[95]、Jaccard系数JAC[96]等评价标准.
| 表 3 用于评价血管分割的参数表 |
灵敏度和特异度是指在预测为真或者假里面分别真实为真或者假的概率, 其定义分别如式(4)和式(5)所示.
| ${\text{灵敏度}}{{ = }}\dfrac{{{{TP}}}}{{TP + FN}}$ | (4) |
| ${\text{特异度}}{\rm{ = }}\dfrac{{{{TN}}}}{{TN + F{\rm{P}}}}$ | (5) |
准确率关注的是分割结果中有多少是正确的, 召回率关注的是有多少血管部分被正确地预测处理, 其定义分别如式(6)和式(7)所示.
| ${\text{准确率}}{\rm{ = }}\dfrac{{{{TP}}}}{{TP + F{{P}}}}$ | (6) |
| ${\text{召回率}}{\rm{ = }}\dfrac{{{{TP}}}}{{TP + FN}}$ | (7) |
事实上, 准确率P和召回率R互相矛盾, P高时, R就低, R高时, P就低. 所以为了综合评价分割性能, 引入P-R曲线, P-R曲线也可根据其曲线下面积AUC (Area Under Curve)来对图像的分割效果进行评估[97], AUC越大, 其性能越好. 此外, F1度量也可以综合准确率和召回率, 其定义如式(8)所示.
| ${{F1 = }}\dfrac{{{{2PR}}}}{{P + R}} = \dfrac{{{{2TP}}}}{{TP + FP + TN + FN}}$ | (8) |
F1度量值越大, 其性能越好. DICE相似系数是F1度量的另一种表达形式, 其定义如式(9)所示.
| $DSC{\rm{ = }}\dfrac{{{{2TP}}}}{{TP{{ + FN}} + TN + FP}} = \dfrac{{2\left| {X \cap Y} \right|}}{{X + Y}}$ | (9) |
其中, X表示实际的目标血管区域, Y表示分割方法分割的血管区域. DSC值越大, 表明分割方法分割的目标血管和实际血管区域重合度更高.
阴性预测值NPV和阳性预测值PPV这两个评价标准建立在算法已经对图像中的像素做出预测的基础上. NPV表示如果算法将像素预测为非血管部分, 该像素被正确预测的概率, 如式(10)所示, PPV表示如果算法将像素预测为血管, 该像素被正确预测的概率, 如式(11)所示.
边界误差可以反映在血管的边界算法的分割效果优劣, 边界误差越小, 算法效果越佳, 计算方法如式(12)所示.
| $NPV{\rm{ = }}\dfrac{{{{TN}}}}{{TN{{ + FN}}}}$ | (10) |
| $PPV = \dfrac{{TP}}{{TP + FP}}$ | (11) |
| ${\text{边界误差}}{{ = }}\dfrac{{{{FP}} + FN}}{{TP + FN}}$ | (12) |
平均绝对误差MAD计算分割方法的分割结果边缘上每个点
| $MAD = \dfrac{1}{{{N_a}}}\displaystyle \sum\limits_{i = 1}^{{N_a}} {\left[ {\mathop {\min }\limits_j {{\left\| {{o_i}^a - {o_j}^g} \right\|}_2}} \right]} $ | (13) |
豪斯多夫距离HD是描述两组点集之间相似程度的一种度量, 其定义如式(14)所示.
| $HD{\rm{ = }}\max \left( {h\left( {{O_a},{O_g}} \right),h\left( {{O_g},{O_a}} \right)} \right)$ | (14) |
其中,
Jaccard系数(JAC)用于比较有限样本集合之间的相似性和差异性, 它的定义是集合α和β交集的大小与其并集大小的一个比值, 如式(15)所示, 如果Jaccard系数越大, 则说明他们的相似度越高.
| $J\left( {\alpha ,\beta } \right) = \dfrac{{\left| {\alpha \cap \beta } \right|}}{{\left| {\alpha \cup \beta } \right|}}$ | (15) |
Brieva等[65]在评价水平集分割效果的时候, 设计了SA参数来评价分割的效果, 如式(16)所示, 又根据SA参数分别针对边界和区域, 进而定义SAC和SAR两个参数.
| $SA{\rm{ = }}\frac{{\text{正确检测到的像素数量}}}{{\text{像素总数}}}$ | (16) |
Khaleel等[51]在提取血管树时, 引入了灰度直方图和其均值的误差平方和SSE, 如式(17)所示. 选取其中最小的SSE作为分割效果最佳的图片. 其中n是一组血管造影图像的数量, yi是血管造影图像的直方图,
| $SSE{\rm{ = }}{\sum\limits_{i = 1}^{\rm{n}} {\left( {{y_i} - {{\overset{\frown} y}_i}} \right)} ^2}$ | (17) |
表4是文中所提到的方法在评价其分割效果时所使用的评价标准及其对应参考文献.
| 表 4 评价标准及其参考文献 |
4 展望
在医学临床应用中, 计算机辅助技术和医学图像分割技术是疾病诊断的常用手段, 基于血管造影的DSA图像分割技术是相关血管疾病量化分析描述和血管三维重建的前提, 造影图像的分割意义重大, 分析以上所罗列的分割方法主要从以下几个方面对心血管造影图像分割的未来发展做出展望:
(1)建立心血管造影图像相关的公开金标准数据集. 心血管造影图像目前还没有公开的数据集, 没有一个统一的标准对各论文所提出的方法进行评估和比较, 不利于不同分割方法直接的横向对比. 在获取心血管造影图像时, 需要对患者的隐私进行脱敏保护, 只保留影像序号、图像拍摄日期、体位角度等非敏感信息[83]. 由于心血管造影图像在造影时注射的造影剂浓度会有差异, 得到的图像的对比度清晰度也会有差异, 且造影图像分为左视角和右视角, 在制造金标准时也需要综合考虑这些情况. 如果需要进一步研究, 还可建立不同病变的数据分类, 根据不同的病变建立相应数据集. 此外, 制作金标准的相关“专家”不能只有一个, 一方面因为人工对样本进行勾画时存在误差, 另一方面, 对于边界的判定带有一些主观因素, 制作的金标准数据集必须结合多个专家的分割结果.
(2)提升造影图像的增强效果. 预处理作为分割操作的第一步必不可少, 对图像中无关噪声部分的降噪以及目标部分的增强, 可以借鉴文章中所总结的几种方法, 向“自适应”, “多模板”方向发展, 使得预处理之后的图像最大限度地保留细小血管的信息, 且尽可能使得目标区域和背景区域的对比度拉大.
(3)开发全自动的分割方法. 分割方法中, 基于区域生长和基于轨迹追踪的方法都需要人工设定初始点, 这在实际使用中会造成不便捷, 且人工设定点的差异对整体的分割结果会产生影响. 所以如果能够实现全自动的分割对于提高工作效率和分割效果十分有帮助. 近几年, 使用机器学习方法的相关研究占主要地位, 使用这种方法可以实现自动化分割, 但是前期训练过程十分繁琐, 如何提高效率是一个巨大挑战.
(4)将分割结果用于后续冠脉狭窄程度量化, 可以积累狭窄程度和血管宽度变化规律的先验知识, 实现血管狭窄程度的自动测量[99], 自动定位病变区域. 分割质量高的图像可以极大便利医生进行QCA测评[86], 辅助医生进行诊断以及后续Syntax系统评分. 现有的全自动QCA[85]过程准确率还有待提高, 可以引入新的神经网络或者补充训练数据来提高其准确率, 减轻人工负担.
(5)引入造影图像序列, 对动态的造影图像进行运动跟踪和分割, 由于细小血管基本分布在血管末梢, 其造影剂达到的时间较晚, 显影较晚, 且显影剂的效果也随时间流逝变得不明显, 导致细小血管的分割难度大, 效果不佳. 如果能够综合数张造影图像, 可以使得分割效果更加, 得到病变处最窄部分的狭窄程度[100], 提高诊断的准确度.
(6)进一步研究血管的中心线提取, 口径测量, 血管内部导管的分割等工作, 造影血管的分割是众多研究内容所需要涉及到的, 只是心血管疾病诊断等相关研究中一个重要环节.
5 结束语本文从图像预处理、分割方法以及评价标准3个方面, 研究了心血管DSA图像处理的流程方法. 但所提及的各种方法只是涉及分割技术, 后续对血管的定量分析如狭窄程度分析等并未涉及, 且所介绍的每种方法有其特有的适用范围, 根据数据源的不同, 其分割方法和处理方法也各异, 并不存在一种最好的分割处理方法, 在实际情况中, 需要针对特定情况进行分析, 不断尝试使用不同方法的搭配组合或者设计新的方法使得分割血管的效果更佳.
| [1] |
Wang H, Abajobir AA, Abate KH, et al. Global, regional, and national under-5 mortality, adult mortality, age-specific mortality, and life expectancy, 1970–2016: A systematic analysis for the Global Burden of Disease Study 2016. The Lancet, 2017, 390(10100): 1084-1150. DOI:10.1016/S0140-6736(17)31833-0 |
| [2] |
World Health Organization. World health statistics 2016: Monitoring health for the SDGs, Sustainable Development Goals. Geneva, Switzerland: WHO. 2016. 293–328.
|
| [3] |
Woodruffe S, Neubeck L, Clark RA, et al. Australian Cardiovascular health and Rehabilitation Association (ACRA) core components of cardiovascular disease secondary prevention and cardiac rehabilitation 2014. Heart, Lung and Circulation, 2015, 24(5): 430-441. DOI:10.1016/j.hlc.2014.12.008 |
| [4] |
Kirişli HA, Schaap M, Metz CT, et al. Standardized evaluation framework for evaluating coronary artery stenosis detection, stenosis quantification and lumen segmentation algorithms in computed tomography angiography. Medical Image Analysis, 2013, 17(8): 859-876. DOI:10.1016/j.media.2013.05.007 |
| [5] |
李裕. 基于CCA和CCTA图像的冠状动脉狭窄度量化方法研究[硕士学位论文]. 西安: 西安电子科技大学, 2018.
|
| [6] |
Kulathilake KASH, Ranathunga L, Constantine GR, et al. Region growing segmentation method for extracting vessel structures from coronary cine-angiograms. Proceedings of 2015 Moratuwa Engineering Research Conference (MERCon). Moratuwa, Sri Lanka. 2015. 142–147.
|
| [7] |
Moccia S, De Momi E, El Hadji S, et al. Blood vessel segmentation algorithms—review of methods, datasets and evaluation metrics. Computer Methods and Programs in Biomedicine, 2018, 158: 71-91. DOI:10.1016/j.cmpb.2018.02.001 |
| [8] |
Kirbas C, Quek F. A review of vessel extraction techniques and algorithms. ACM Computing Surveys, 2004, 36(2): 81-121. DOI:10.1145/1031120.1031121 |
| [9] |
Sun KQ. Development of segmentation methods for vascular angiogram. IETE Technical Review, 2011, 28(5): 392-399. DOI:10.4103/0256-4602.85970 |
| [10] |
Tayebi RM, Sulaiman PSB, Wirza R, et al. Coronary artery segmentation in angiograms with pattern recognition techniques-a survey. Proceedings of 2013 International Conference on Advanced Computer Science Applications and Technologies. Kuching, Malaysia. 2013. 321–326.
|
| [11] |
Khan MI, Shaikh H, Mansuri AM, et al. A review of retinal vessel segmentation techniques and algorithms. International Journal of Computer Technology and Applications, 2011, 2(5): 1140-1144. |
| [12] |
Reza AM. Realization of the Contrast Limited Adaptive Histogram Equalization (CLAHE) for real-time image enhancement. Journal of VLSI Signal Processing Systems for Signal, Image and Video Technology, 2004, 38(1): 35-44. DOI:10.1023/B:VLSI.0000028532.53893.82 |
| [13] |
Zeng M, Li YF, Meng QH, et al. Improving histogram-based image contrast enhancement using gray-level information histogram with application to X-ray images. Optik, 2012, 123(6): 511-520. DOI:10.1016/j.ijleo.2011.05.017 |
| [14] |
陈建辉, 赵蕾, 李德玉, 等. 基于冠脉造影图像血管树分割的血管狭窄自动识别方法. 中国生物医学工程学报, 2019, 38(3): 266-272. DOI:10.3969/j.issn.0258-8021.2019.03.002 |
| [15] |
Poli R, Valli G. An algorithm for real-time vessel enhancement and detection. Computer Methods and Programs in Biomedicine, 1997, 52(1): 1-22. DOI:10.1016/S0169-2607(96)01773-7 |
| [16] |
陈楷丰. 基于非线性滤波的冠脉造影图像增强算法的研究[硕士学位论文]. 大连: 大连海事大学, 2016.
|
| [17] |
Oh J, Hwang H. Feature enhancement of medical images using morphology-based homomorphic filter and differential evolution algorithm. International Journal of Control, Automation and Systems, 2010, 8(4): 857-861. DOI:10.1007/s12555-010-0418-y |
| [18] |
Frangi AF, Niessen WJ, Vincken KL, et al. Muliscale vessel enhancement filtering. Proceedings of 1st International Conference on Medical Image Computing and Computer-Assisted Intervention. Cambridge, UK. 1998. 130–137.
|
| [19] |
Conn AR, Gould N, Toint PL. Large-scale nonlinear constrained optimization: A current survey. Spedicato E. Algorithms for Continuous Optimization. Dordrecht: Springer, 1994. 287–332.
|
| [20] |
Florack LMJ, Romeny BMTH, Koenderink JJ, et al. Scale and the differential structure of images. Image and Vision Computing, 1992, 10(6): 376-388. DOI:10.1016/0262-8856(92)90024-W |
| [21] |
Truc PTH, Khan MAU, Lee YK, et al. Vessel enhancement filter using directional filter bank. Computer Vision and Image Understanding, 2009, 113(1): 101-112. DOI:10.1016/j.cviu.2008.07.009 |
| [22] |
Xu X, Liu B, Zhou FG. Hessian-based vessel enhancement combined with directional filter banks and vessel similarity. Proceedings of 2013 ICME International Conference on Complex Medical Engineering. Beijing, China. 2013. 80–84.
|
| [23] |
Zai S, Abbas A. An effective enhancement and segmentation of coronary arteries in 2D Angiograms. Proceedings of 2018 International Conference on Smart Computing and Electronic Enterprise (ICSCEE). Shah Alam, Malaysia. 2018. 1–4.
|
| [24] |
Zhang F, Zhang XH, Liu XX, et al. Blood vessel enhancement for DSA images based on adaptive multi-scale filtering. Optik, 2014, 125(10): 2383-2388. DOI:10.1016/j.ijleo.2013.10.111 |
| [25] |
Li Q, Sone S, Doi K. Selective enhancement filters for nodules, vessels, and airway walls in two- and three-dimensional CT scans. Medical Physics, 2003, 30(8): 2040-2051. DOI:10.1118/1.1581411 |
| [26] |
Zhou SJ, Yang J, Chen WF, et al. New approach to the automatic segmentation of coronary artery in X-ray angiograms. Science in China Series F: Information Sciences, 2008, 51(1): 25-39. DOI:10.1007/s11432-008-0005-5 |
| [27] |
Tsai YC, Lee HJ, Chen MYC. Automatic segmentation of vessels from angiogram sequences using adaptive feature transformation. Computers in Biology and Medicine, 2015, 62: 239-253. DOI:10.1016/j.compbiomed.2015.04.029 |
| [28] |
Angulo J. Morphological colour operators in totally ordered lattices based on distances: Application to image filtering, enhancement and analysis. Computer Vision and Image Understanding, 2007, 107(1–2): 56-73. |
| [29] |
Oliveira MA, Leite NJ. A multiscale directional operator and morphological tools for reconnecting broken ridges in fingerprint images. Pattern Recognition, 2008, 41(1): 367-377. DOI:10.1016/j.patcog.2007.05.019 |
| [30] |
De I, Chanda B, Chattopadhyay B. Enhancing effective depth-of-field by image fusion using mathematical morphology. Image and Vision Computing, 2006, 24(12): 1278-1287. DOI:10.1016/j.imavis.2006.04.005 |
| [31] |
Jalba AC, Wilkinson MHF, Roerdink JBTM. Morphological hat-transform scale spaces and their use in pattern classification. Pattern Recognition, 2004, 37(5): 901-915. DOI:10.1016/j.patcog.2003.09.009 |
| [32] |
Sun KQ, Chen Z, Jiang SF, et al. Morphological multiscale enhancement, fuzzy filter and watershed for vascular tree extraction in angiogram. Journal of Medical Systems, 2011, 35(5): 811-824. DOI:10.1007/s10916-010-9466-3 |
| [33] |
Bai XZ, Zhou FG, Xue BD. Image enhancement using multi scale image features extracted by top-hat transform. Optics & Laser Technology, 2012, 44(2): 328-336. |
| [34] |
Fazlali HR, Karimi N, Soroushmehr SMR, et al. Vessel segmentation and catheter detection in X-ray angiograms using superpixels. Medical & Biological Engineering & Computing, 2018, 56(9): 1515-1530. |
| [35] |
Prasad VSN, Domke J. Gabor filter visualization. Journal of Atmosphere Science, 2005, 13: 2005. |
| [36] |
Cruz-Aceves I, Oloumi F, Rangayyan RM, et al. Automatic segmentation of coronary arteries using Gabor filters and thresholding based on multiobjective optimization. Biomedical Signal Processing and Control, 2016, 25: 76-85. DOI:10.1016/j.bspc.2015.11.001 |
| [37] |
王光磊, 王鹏宇, 王中阳, 等. 基于自动随机游走的DSA图像分割算法. 激光杂志, 2018, 39(4): 81-85. |
| [38] |
Wang S, Li BN, Zhou SJ. A segmentation method of coronary angiograms based on multi-scale filtering and region-growing. Proceedings of 2012 International Conference on Biomedical Engineering and Biotechnology. Macao, China. 2012. 678–681.
|
| [39] |
Plourde M, Duong L. Multi scale classification approach for coronary artery detection from X-ray angiography. Proceedings of 2012 11th International Conference on Information Science, Signal Processing and their Applications (ISSPA). Montreal, QC, Canada. 2012. 181–186.
|
| [40] |
Kerkeni A, Benabdallah A, Manzanera A, et al. A coronary artery segmentation method based on multiscale analysis and region growing. Computerized Medical Imaging and Graphics, 2016, 48: 49-61. DOI:10.1016/j.compmedimag.2015.12.004 |
| [41] |
Wink O, Niessen WJ, Viergever MA. Multiscale vessel tracking. IEEE Transactions on Medical Imaging, 2004, 23(1): 130-133. DOI:10.1109/TMI.2003.819920 |
| [42] |
庄宇, 陈光彪, 付庄. 心血管造影图像的分割与诊断. 机械与电子, 2018, 36(4): 16-19, 37. DOI:10.3969/j.issn.1001-2257.2018.04.004 |
| [43] |
Wan T, Shang XQ, Yang WL, et al. Automated coronary artery tree segmentation in X-ray angiography using improved Hessian based enhancement and statistical region merging. Computer Methods and Programs in Biomedicine, 2018, 157: 179-190. DOI:10.1016/j.cmpb.2018.01.002 |
| [44] |
Zhou SJ, Yang J, Wang YT, et al. Automatic segmentation of coronary angiograms based on fuzzy inferring and probabilistic tracking. Biomedical Engineering Online, 2010, 9(1): 40. DOI:10.1186/1475-925X-9-40 |
| [45] |
Dehkordi MT, Hoseini AMD, Sadri S, et al. Local feature fitting active contour for segmenting vessels in angiograms. IET Computer Vision, 2014, 8(3): 161-170. DOI:10.1049/iet-cvi.2013.0083 |
| [46] |
M’hiri F, Duong L, Desrosiers C, et al. Vesselwalker: Coronary arteries segmentation using random walks and hessian-based vesselness filter. Proceedings of 2013 IEEE 10th International Symposium on Biomedical Imaging. San Francisco, CA, USA. 2013. 918–921.
|
| [47] |
Nasr-Esfahani E, Samavi S, Karimi N, et al. Vessel extraction in X-ray angiograms using deep learning. Proceedings of 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Orlando, FL, USA. 2016. 643–646.
|
| [48] |
Nasr-Esfahani E, Karimi N, Jafari MH, et al. Segmentation of vessels in angiograms using convolutional neural networks. Biomedical Signal Processing and Control, 2018, 40: 240-251. DOI:10.1016/j.bspc.2017.09.012 |
| [49] |
Sezgin M, Sankur B. Survey over image thresholding techniques and quantitative performance evaluation. Journal of Electronic Imaging, 2004, 13(1): 146-168. DOI:10.1117/1.1631315 |
| [50] |
Otsu N. A threshold selection method from gray-level histograms. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66. DOI:10.1109/TSMC.1979.4310076 |
| [51] |
Khaleel HH, Rahmat ROK, Zamrin DM, et al. Extraction of coronary artery trees in angiocardiography images. Scientific Research and Essays, 2012, 7(47): 4014-4036. |
| [52] |
Lian YX, Wang YY, Yu JH, et al. Segmentation of arteriovenous malformations nidus and vessel in digital subtraction angiography images based on an iterative thresholding method. Proceedings of 2015 8th International Conference on Biomedical Engineering and Informatics (BMEI). Shenyang, China. 2015. 111–115.
|
| [53] |
Yi J, Ra JB. A locally adaptive region growing algorithm for vascular segmentation. International Journal of Imaging Systems and Technology, 2003, 13(4): 208-214. DOI:10.1002/ima.10059 |
| [54] |
Chen Y, Cao Q, Zhuang ZK, et al. 3-D coronary vessel extraction using a novel minimum path based region growing. Proceedings of the 10th International Conference on Image Analysis and Recognition. Póvoa do Varzim, Portugal. 2013. 502–509.
|
| [55] |
Sekiguchi H, Sugimoto N, Eiho S, et al. Blood vessel segmentation for head MRA using branch-based region growing. Systems and Computers in Japan, 2005, 36(5): 80-88. DOI:10.1002/scj.20166 |
| [56] |
Li YL, Zhou SJ, Wu JH, et al. A novel method of vessel segmentation for X-ray coronary angiography images. Proceedings of 2012 Fourth International Conference on Computational and Information Sciences. Chongqing, China. 2012. 468–471.
|
| [57] |
Nock R, Nielsen F. Statistical region merging. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(11): 1452-1458. DOI:10.1109/TPAMI.2004.110 |
| [58] |
Chaudhuri S, Chatterjee S, Katz N, et al. Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Transactions on Medical Imaging, 1989, 8(3): 263-269. DOI:10.1109/42.34715 |
| [59] |
Cruz-Aceves I, Hernandez-Aguirre A, Valdez SI. On the performance of nature inspired algorithms for the automatic segmentation of coronary arteries using Gaussian matched filters. Applied Soft Computing, 2016, 46: 665-676. DOI:10.1016/j.asoc.2016.01.030 |
| [60] |
Cruz-Aceves I, Cervantes-Sanchez F, Avila-Garcia MS. A novel multiscale gaussian-matched filter using neural networks for the segmentation of X-ray coronary angiograms. Journal of Healthcare Engineering, 2018, 2018: 5812059. |
| [61] |
Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. International Journal of Computer Vision, 1988, 1(4): 321-331. DOI:10.1007/BF00133570 |
| [62] |
Osher S, Sethian JA. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. Journal of Computational Physics, 1988, 79(1): 12-49. DOI:10.1016/0021-9991(88)90002-2 |
| [63] |
Xu CY, Prince JL. Generalized gradient vector flow external forces for active contours. Signal Processing, 1998, 71(2): 131-139. DOI:10.1016/S0165-1684(98)00140-6 |
| [64] |
Devi SN, Kumaravel N. Comparison of active contour models for image segmentation in X-ray coronary angiogram images. Journal of Medical Engineering & Technology, 2008, 32(5): 408-418. |
| [65] |
Brieva J, Gonzalez E, Gonzalez F, et al. A level set method for vessel segmentation in coronary angiography. Proceedings of 2005 IEEE Engineering in Medicine and Biology 27th Annual Conferenc. Shanghai, China. 2006. 6348–6351.
|
| [66] |
Sum KW, Cheung PYS. Vessel extraction under non-uniform illumination: A level set approach. IEEE Transactions on Biomedical Engineering, 2008, 55(1): 358-360. DOI:10.1109/TBME.2007.896587 |
| [67] |
Khokhar M, Talpur S, Khowaja SA, et al. A novel curvature feature embedded level set method for image segmentation of coronary angiograms. In: Rocha Á, Adeli H, Reis L, eds, et al. Trends and Advances in Information Systems and Technologies. Cham: Springer, 2018. 831–841.
|
| [68] |
Wang L, He L, Mishra A, et al. Active contours driven by local Gaussian distribution fitting energy. Signal Processing, 2009, 89(12): 2435-2447. DOI:10.1016/j.sigpro.2009.03.014 |
| [69] |
Sun KQ, Chen Z, Jiang SF. Local morphology fitting active contour for automatic vascular segmentation. IEEE Transactions on Biomedical Engineering, 2012, 59(2): 464-473. DOI:10.1109/TBME.2011.2174362 |
| [70] |
Li H, Yezzi A. Vessels as 4-D Curves: Global minimal 4-D paths to extract 3-D tubular surfaces and centerlines. IEEE Transactions on Medical Imaging, 2007, 26(9): 1213-1223. DOI:10.1109/TMI.2007.903696 |
| [71] |
Benmansour F, Cohen L D. Tubular structure segmentation based on minimal path method and anisotropic enhancement. International Journal of Computer Vision, 2011, 92(2): 192-210. DOI:10.1007/s11263-010-0331-0 |
| [72] |
Hernandez-Vela A, Gatta C, Escalera S, et al. accurate coronary centerline extraction, caliber estimation, and catheter detection in angiographies. IEEE Transactions on Information Technology in Biomedicine, 2012, 16(6): 1332-1340. DOI:10.1109/TITB.2012.2220781 |
| [73] |
Giger M L. Machine learning in medical imaging. Journal of The American College of Radiology, 2018, 15(3): 512-520. DOI:10.1016/j.jacr.2017.12.028 |
| [74] |
Greenspan H, Van Ginneken B, Summers RM. Guest editorial deep learning in medical imaging: Overview and future promise of an exciting new technique. IEEE Transactions on Medical Imaging, 2016, 35(5): 1153-1159. DOI:10.1109/TMI.2016.2553401 |
| [75] |
Nekovei R, Sun Y. Back-propagation network and its configuration for blood vessel detection in angiograms. IEEE Transactions on Neural Networks, 1995, 6(1): 64-72. DOI:10.1109/72.363449 |
| [76] |
Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems. Red Hook, NY, USA. 2012. 1097–1105.
|
| [77] |
Litjens G, Kooi T, Bejnordi BE, et al. A survey on deep learning in medical image analysis. Medical Image Analysis, 2017, 42: 60-88. DOI:10.1016/j.media.2017.07.005 |
| [78] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. Proceedings of 18th International Conference on Medical Image Computing and Computer-Assisted Intervention. Munich, Germany. 2015. 234–241.
|
| [79] |
Yang SY, Yang J, Wang YC, et al. Automatic coronary artery segmentation in X-ray angiograms by multiple convolutional neural networks. Proceedings of the 3rd International Conference on Multimedia and Image Processing. New York, NY, USA. 2018.31–35.
|
| [80] |
Jo K, Kweon J, Kim YH, et al. Segmentation of the main vessel of the left anterior descending artery using selective feature mapping in coronary angiography. IEEE Access, 2019, 7: 919-930. DOI:10.1109/ACCESS.2018.2886009 |
| [81] |
Zhao L, Li DY, Chen JH, et al. Automated coronary tree segmentation for X-ray angiography sequences using fully-convolutional neural networks. Proceedings of 2018 IEEE Visual Communications and Image Processing (VCIP). Taichung, China. 2018. 1–4.
|
| [82] |
Caelles S, Maninis K K, Pont-Tuset J, et al. One-shot video object segmentation. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA. 2017. 221–230.
|
| [83] |
杨少戈. 基于深度学习的冠脉造影图像分割[硕士学位论文]. 北京: 北京邮电大学, 2019.
|
| [84] |
Yang S, Kweon J, Kim YH. Major vessel segmentation on X-ray coronary angiography using deep networks with a novel penalty loss function. Proceedings of Machine Learning Research. London, UK. 2019.
|
| [85] |
Au B, Shaham U, Dhruva S, et al. Automated characterization of stenosis in invasive coronary angiography images with convolutional neural networks. arXiv preprint arXiv: 1807.10597, 2018.
|
| [86] |
Zhang HB, Mu L, Hu S, et al. Comparison of physician visual assessment with quantitative coronary angiography in assessment of stenosis severity in China. JAMA Internal Medicine, 2018, 178(2): 239-247. DOI:10.1001/jamainternmed.2017.7821 |
| [87] |
Fan JF, Yang J, Wang YC, et al. Multichannel fully convolutional network for coronary artery segmentation in X-Ray angiograms. IEEE Access, 2018, 6: 44635-44643. DOI:10.1109/ACCESS.2018.2864592 |
| [88] |
Jun TJ, Kweon J, Kim YH, et al. T-Net: Nested encoder-decoder architecture for the main vessel segmentation in coronary angiography. arXiv preprint arXiv: 1905.04197, 2019.
|
| [89] |
Lassó A, Trucco E. Vessel enhancement in digital X-ray angiographic sequences by temporal statistical learning. Computerized Medical Imaging and Graphics, 2005, 29(5): 343-355. DOI:10.1016/j.compmedimag.2005.02.002 |
| [90] |
Achanta R, Shaji A, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282. DOI:10.1109/TPAMI.2012.120 |
| [91] |
Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation. IEEE Transactions on Medical Imaging, 2004, 23(7): 903-921. DOI:10.1109/TMI.2004.828354 |
| [92] |
周志华. 机器学习. 北京: 清华大学出版社, 2016. 425.
|
| [93] |
Wan T, Cao JJ, Chen JH, et al. Automated grading of breast cancer histopathology using cascaded ensemble with combination of multi-level image features. Neurocomputing, 2017, 229: 34-44. DOI:10.1016/j.neucom.2016.05.084 |
| [94] |
Hosseini M P, Nazem-Zadeh M R, Pompili D, et al. Comparative performance evaluation of automated segmentation methods of hippocampus from magnetic resonance images of temporal lobe epilepsy patients. Medical Physics, 2016, 43(1): 538-553. DOI:10.1118/1.4938411 |
| [95] |
Dice LR. Measures of the amount of ecologic association between species. Ecology, 1945, 26(3): 297-302. DOI:10.2307/1932409 |
| [96] |
Hamers L, Hemeryck Y, Herweyers G, et al. Similarity measures in scientometric research: The Jaccard index versus Salton’s cosine formula. Information Processing & Management, 1989, 25(3): 315-318. |
| [97] |
Bradley AP. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition, 1997, 30(7): 1145-1159. DOI:10.1016/S0031-3203(96)00142-2 |
| [98] |
Carballal A, Novoa FJ, Fernandez-Lozano C, et al. Automatic multiscale vascular image segmentation algorithm for coronary angiography. Biomedical Signal Processing and Control, 2018, 46: 1-9. DOI:10.1016/j.bspc.2018.06.007 |
| [99] |
Zhang D, Yang G, Zhao S, et al. Direct quantification for coronary artery stenosis using multiview learning. arXiv preprint arXiv: 1907.10032, 2019.
|
| [100] |
Compas CB, Syeda-Mahmood T, McNeillie P, et al. Automatic detection of coronary stenosis in X-ray angiography through spatio-temporal tracking. Proceedings of 2014 IEEE 11th international symposium on biomedical imaging (ISBI). Beijing, China. 2014. 1299–1302.
|
 2001, Vol. 29
2001, Vol. 29



