2. 中国科学院 沈阳计算技术研究所, 沈阳 110168
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China
近年来, 随着物流行业的发展, 现代仓储物流企业对自动化仓库AS/RS (Automated Storage and Retrieval System)的效率要求也越来越高, 在AS/RS中, 出入库货物搬运任务完全由自动化巷道式堆垛机来负责完成, 堆垛机作为AS/RS的核心设备, 其调度问题对仓库的管理效率起决定性作用, 目前, 仓库的堆垛机调度路径往往采用直接指派的方式, 导致堆垛机的运行效率低、时间和能耗较高. 良好的堆垛机存取路径优化可以降低仓储成本, 提高AS/RS的利用率, 对仓库管理效率的提升具有很大的现实意义.
通过对堆垛机的运动模式和物理特性进行分析, 发现其调度问题要考虑时间、能耗、作业效率等因素, 这3个因素显然不能同时达到最佳, 那么就需要一些方法来进行协调, 传统的方法是将多个目标函数通过权重分配的方式降维成单个目标函数, 转换成单目标优化的问题, 这种方式存在权重量化设定困难和易于陷入局部最优等问题. 本文采用多目标优化方式[1]来解决路径优化问题, 对多个无法同时达到最优的目标进行协调, 产生一组Pareto最优解[2]路径, 供仓库控制系统自行选择.
针对堆垛机调度问题, 关榆君等[3]采用引入了交算子和交序列的猫群算法, 但无法得到Pareto最优解集, 依旧是单目标优化的变种. 针对多目标优化问题, Srinivas和Deb 在NSGA的基础上提出了NSGA-Ⅱ算法[4]来求pareto最优解集, NSGA-Ⅱ算法使用了快速非支配解排序算法降低复杂度、引进了精英策略来保证优良个体得以保留、采用拥挤度替代了共享适应度, NSGA-Ⅱ算法以运行速度快、解集收敛性好、简单有效等特点在多目标优化领域得以广泛应用, 尤其对于低维多目标优化问题具有明显优势[5], 但仍存在着容易陷入局部最小值、局部搜索能力不足等问题[6]. 因此, 本文在NSGA-Ⅱ的基础上进行改进与优化, 对NSGA-Ⅱ算法易陷入局部最优的问题采用引入自适应遗传算子的方式进行了改善, 并新增了局部随机搜索策略增强局部搜索能力. 通过实验证明了新方法对比NSGA-Ⅱ算法在堆垛机调度问题中的有效性.
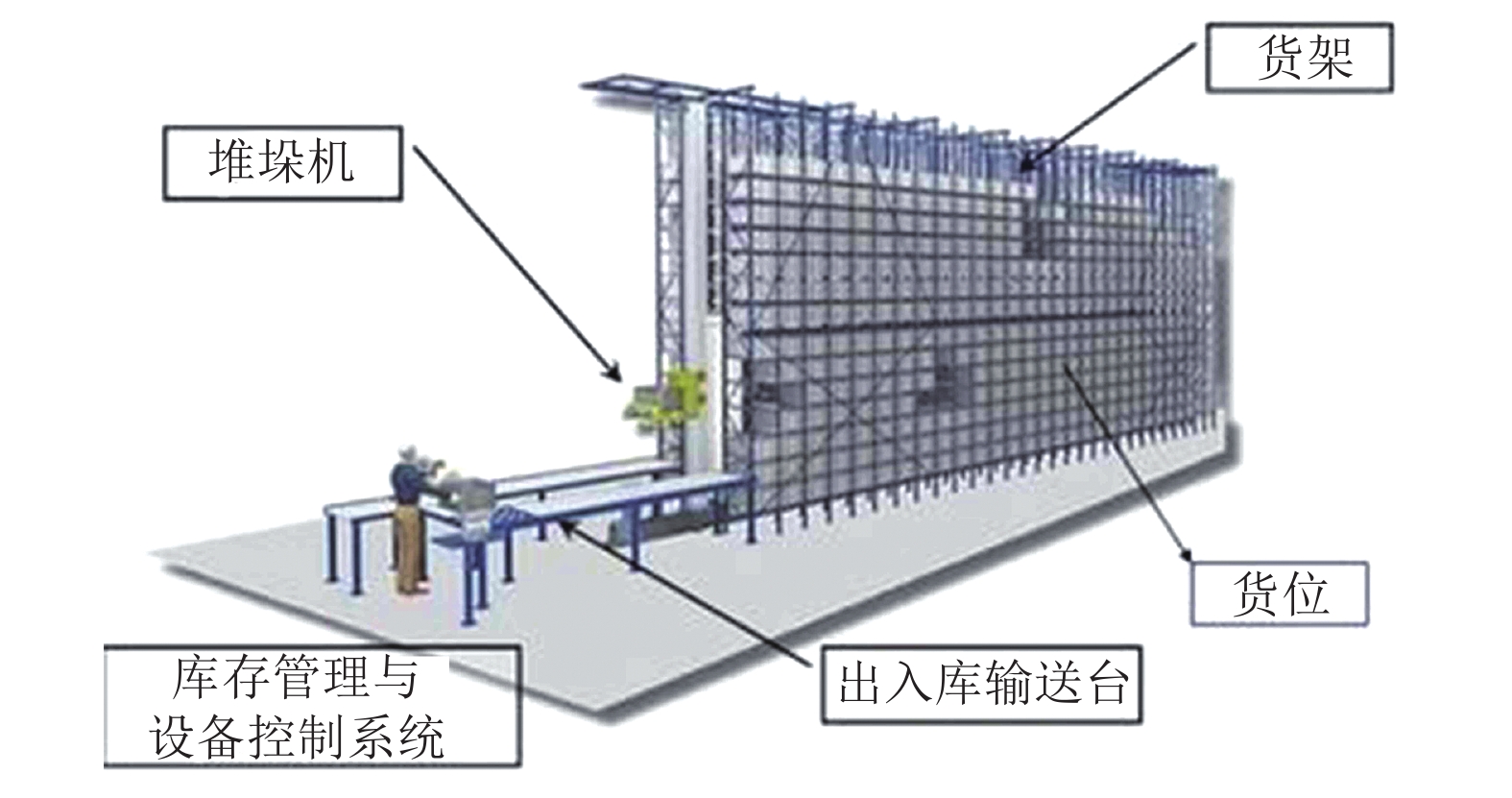
1 堆垛机调度模型 1.1 问题描述以连云港某家氨纶公司的自动化无人仓库为研究对象, 该仓库为同端出/入布局, 即入库口与出库口在巷道的同一侧, 货架沿通道排列, 堆垛机按指令沿通道运行, 进行货架上货物的拣选作业. 图1为部分示意图.
|
图 1 自动化无人仓库部分示意图 |
本文主要研究的是单一堆垛机面对多任务时, 如何合理的设计调度路径. 从时间、能耗、批作业效率3个方面考虑, 这3个指标不能同时达到最优, 故运用算法产生一组Pareto最优解, 供仓库控制系统自行选择, 从而节约堆垛机的使用费用, 提高仓库的搬运效率.
1.2 模型建立堆垛机的运行可以归类为TSP问题, 即机器从起点出发, 一次性经过多个拣选点又回到起点的路径问题. 考虑到堆垛机在运行过程中的时间、能耗以及作业效率, 对堆垛机的调度路径进行建模. 分别从时间、能耗、批作业效率3个方面建立优化目标.
| $\left\{ \begin{array}{l} \min T = \displaystyle\sum\limits_{i = 1}^{m - 1} {{t_{i(i + 1)}}} \\ \min E = \displaystyle\sum\limits_{i = 1}^{m - 1} {{e_{i(i + 1)}}} \\ \min Eff = \displaystyle\sum\limits_{i = 1}^m {{t_{0i}}} \frac{1}{{{f_i}}} \\ \end{array} \right.$ | (1) |
其中,
| ${e_{ij}} = {e_x}\left| {{x_i} - {x_j}} \right| + {e_y}\left| {{y_i} - {y_j}} \right|$ | (2) |
| ${t_{ij}} = \max \left(\dfrac{{\left| {{x_i} - {x_j}} \right|L}}{{V(x)}},\dfrac{{\left| {{y_i} - {y_j}} \right|H}}{{V(y)}}\right)$ | (3) |
其中,
在解决多目标优化问题时, NSGA-Ⅱ算法作为较为经典的一种算法一直得到广泛的应用, 但将其应用到堆垛机调度问题中时, 发现NSGA-Ⅱ算法容易陷入局部最优, 并在搜索能力上有所不足, 因此, 本文在NSGA-Ⅱ算法的基础上从遗传算子着手进行了改进, 并加入了局部随机搜索策略, 得到了一种加入局部搜索策略的自适应遗传算法(IMOGA).
2.1 染色体编码本文采用对堆垛机的货位点拣选顺序进行编码的方式, 染色体由多个基因组成, 每个基因表示货架上的货格编号, 以25列20行的货架为例, 采用行优先的方式对货格进行编号, 第1行第1列编号为0, 第1行第2列编号为1, 依次类推, 一直到编号4999. 以长度为5的染色体为例, 染色体[43, 54, 2, 386, 123]表示堆垛机共经过5个点, 依次为43, 54, 2, 386, 123号货位.
2.2 自适应遗传算子在进化过程中, 出现堆垛机路径序列部分货位点相邻的情况, 以25列20行的货架为例, 对于55号货位, 20、54、56、80号货位都与它相邻, 如图2所示. 为了保证堆垛机的运行效率, 对于这样的相邻货位点序列, 在交叉变异过程中, 应当保证相邻货位点序列不被破坏. 出于以上考虑, 对交叉、变异操作进行了改进.

|
图 2 货位示意图 |
交叉操作采用改进的基于位置的交叉, 首先根据染色体长度L与随机位置数z的关系公式

|
图 3 改进后的交叉操作 |
变异操作采用随机位置的互换操作, 根据染色体长度L与变异点z的关系公式

|
图 4 改进后的变异操作 |
在研究过程中发现, 遗传算子的交叉、变异概率对在很大程度上将影响算法的结果. 对于适应度较差的个体, 应当给予更高的交叉变异概率, 而对于适应度较高的优秀个体, 应当给予较低的交叉变异概率[7], 因此, 根据自适应的思想, 使交叉率变异率按照适应度的Sigmoid曲线进行调整[8], 尽力保留优秀个体的同时跳出局部收敛, 将遗传交叉变异概率做如下改进.
| ${P_c} = \left\{ \begin{array}{l} {P_{c\min }} + \dfrac{{{P_{c\max }} - {P_{c\min }}}}{{1 + \exp [A\dfrac{{2({f^{'}} - {f_{\rm avg}})}}{{{f_{\max }} - {f_{\rm avg}}}}]}},\;\;\;\;{f^{'}} \ge {f_{\rm avg}} \\ {P_{c\max }},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f^{'}} < {f_{\rm avg}} \\ \end{array} \right.$ | (4) |
| ${P_m} = \left\{ \begin{array}{l} {P_{m\min }} + \dfrac{{{P_{m\max }} - {P_{m\min }}}}{{1 + \exp [A\dfrac{{2(f - {f_{\rm avg}})}}{{{f_{\max }} - {f_{\rm avg}}}}]}},\;\;\;\;f \ge {f_{\rm avg}} \\ {P_{m\max }},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f < {f_{\rm avg}} \\ \end{array} \right.$ | (5) |
其中,
遗传算法在前期的搜索过程中主要是对解空间进行全局寻优搜索, 能够搜索到最优解集的大致范围, 到了迭代的后期, 解集较为集中, 就需要考验算法的局部搜索能力, 由于NSGA-Ⅱ算法局部搜索能力不足, 难以得到问题的真正解集. 出于以上的考虑, 本文针对NSGA-Ⅱ遗传算法局部搜索能力不足的问题, 进行了改进, 采用了局部随机搜索策略来帮助算法改善搜索过程.
模拟退火是一种随机寻优的算法, 具有比较强的局部搜索能力, 其Metropolis准则允许一定的概率上接受劣于原解的新解, 从而使算法能够跳离局部最优的陷阱[9], 理论上, 只要迭代次数足够, 就能够搜索到全局最优. 因此, 本文采用基于模拟退火思想的局部随机搜索策略. 模拟退火算法依据Metropolis准则来判断是否接受搜索过程中得到的被原始解所支配的新解, 新解的接受概率公式为:
| $p = \left\{ \begin{array}{l} \exp ( - \dfrac{{f({x_1}) - f({x_0})}}{{kT}}),\;\;\;\;\;f({x_1}) \ge f({x_0}) \\ 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f({x_1}) < f({x_0}) \\ \end{array} \right.$ | (6) |
其中,
| $T(t) = \dfrac{{{T_0}}}{{\log (1 + t)}}$ | (7) |
其中,
Step 1. 设置初始参数: 初始状态温度
Step 2. 遗传算法进化得到非劣解集
Step 3. 若在解
Step 4. 按照新解接受概率公式, 若
Step 5. 若m<M, 跳至Step3.
Step 6. 更新温度T, 迭代次数若超过最大次数, 终止. 否则, 返回Step 2.
3 实验分析为了验证本文所述的改进算法IMOGA的性能, 针对具体的调度序列, 分别采用NSGA-Ⅱ和IMOGA算法进行求解. 以连云港某氨纶公司的自动化无人仓库为例, 货架有11排, 每排有25列20层, 单个货位的长和高均为1 m, 一台堆垛机负责一个巷道内的出入库操作, 依照货位点依次拣选作业, 堆垛机货位拣选点坐标测试数据如下:
| $ \begin{split} D =& [(10,10);(5,2);(17,2);(20,19);(7,5);(15,2);\\ & (9,9);(19,14);(13,2);(23,9);(16,8);(1,5);\\ & (16,19);(8,10);(22,16)] \end{split} $ |
针对上述货位拣选点, 分别使用NSGA-Ⅱ、IMOGA算法对堆垛机路径进行优化. 算法参数: 初始种群大小100, 最大迭代数200, NSGA-Ⅱ的

|
图 5 时间原则算法迭代过程 |

|
图 6 能耗原则算法迭代过程 |
|
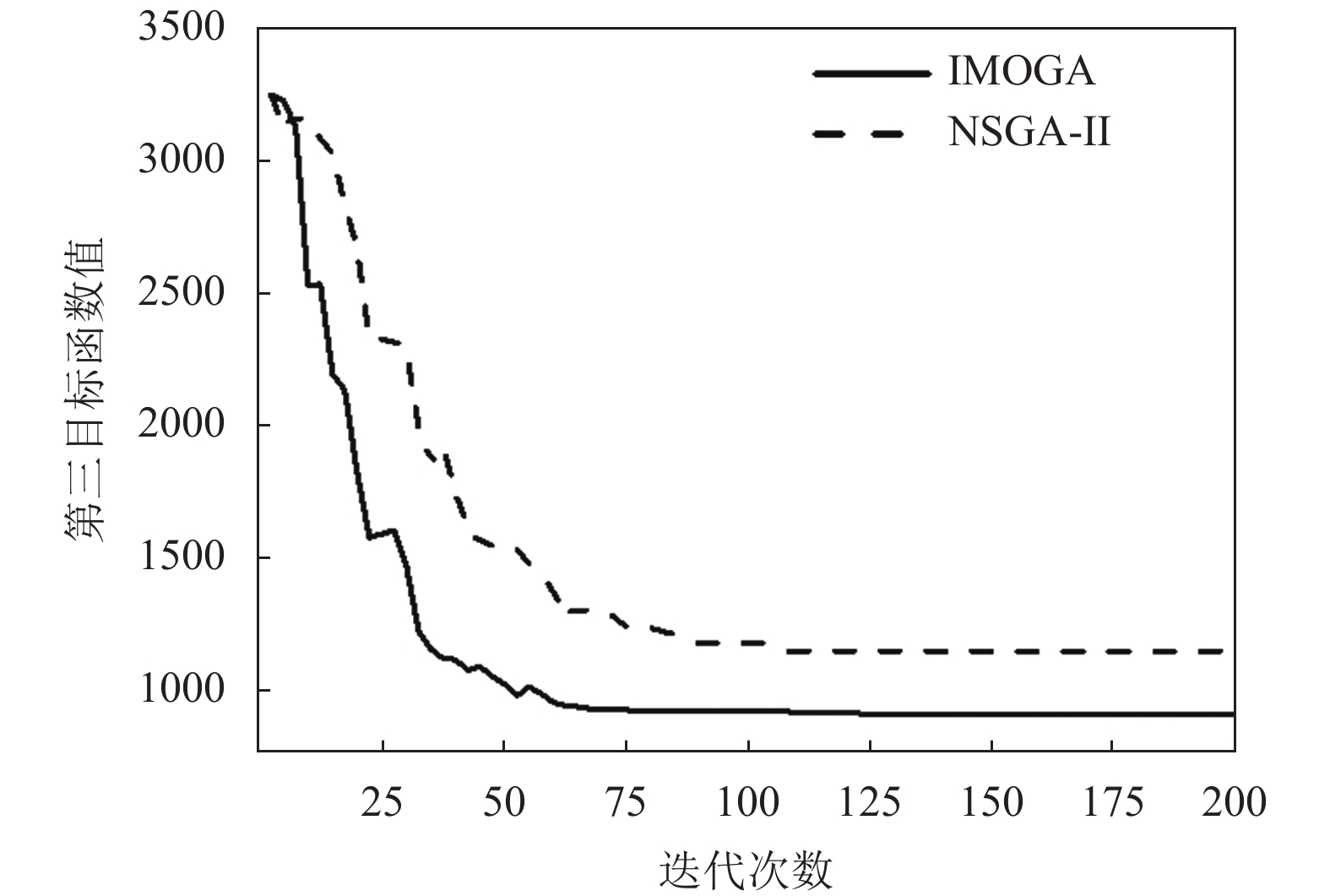
图 7 作业效率原则算法迭代过程 |
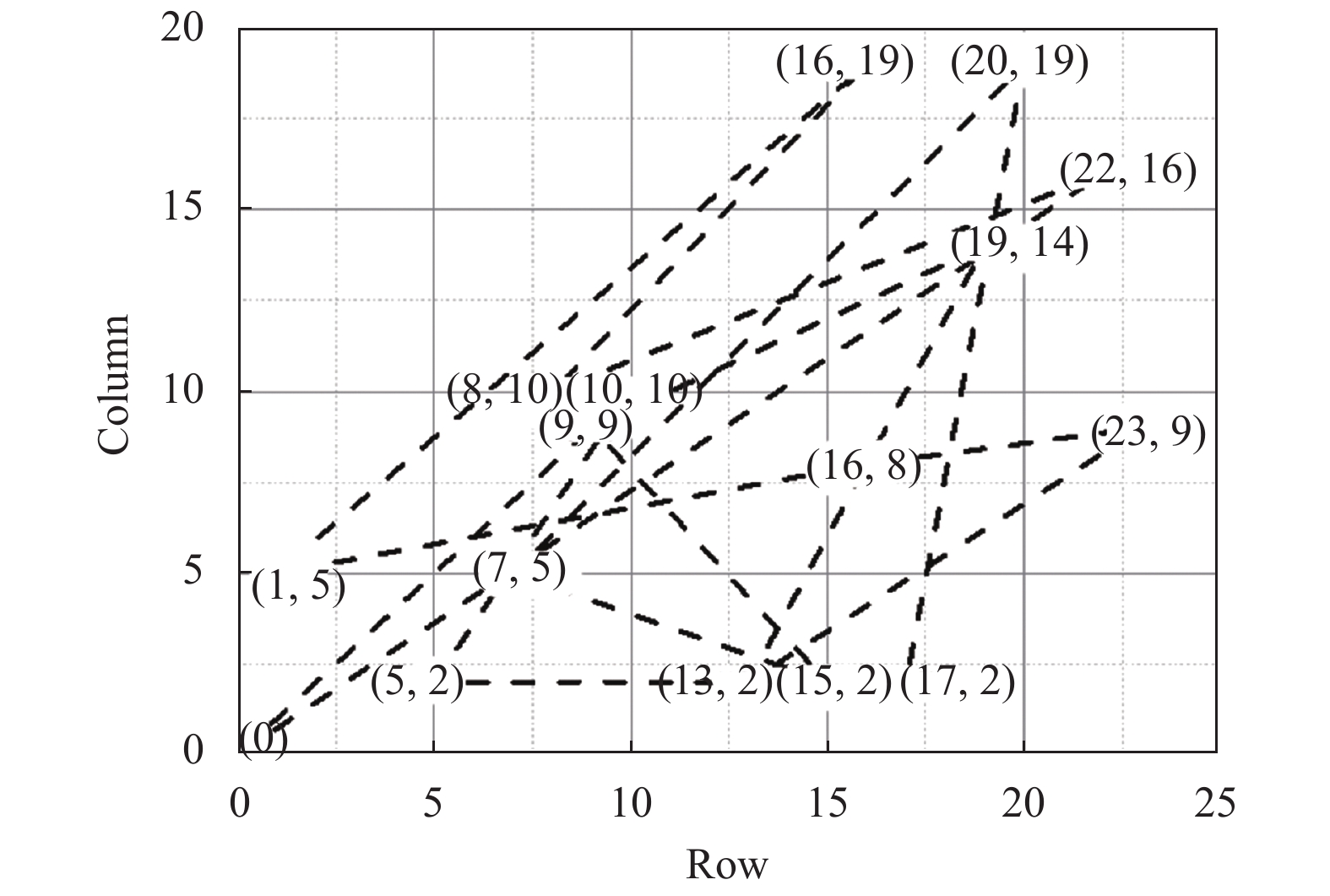
由图5~图7可见, IMOGA较NSGA-Ⅱ收敛速度更快, 趋于稳定的代数更早, 在各个目标函数上的值最优, IMOGA在收敛过程中存在一些拐点, 证明IMOGA在局部随机搜索策略帮助下, 能在一定概率上接受劣解来跳出局部最优. IMOGA算法求得测试数据(图8)的一组路径坐标Pareto解如图9~图11所示.
|
图 8 初始序列路径图 |

|
图 9 Pareto解1路径图 |

|
图 10 Pareto解2路径图 |

|
图 11 Pareto解3路径图 |
采用Knowles, Corne提出的解集与参考集的距离指标
| ${D_{IR}}({S_j}) = \dfrac{1}{{\left| {{S^*}} \right|}}\displaystyle\sum\limits_{y \in {S^*}} {\min \left\{ {{d_{xy}}|x \in {S_j}} \right\}} $ | (8) |
其中,
| ${d_{xy}} = \sqrt {\displaystyle\sum\limits_{i = 1}^N {{{(f_i^*(y) - f_i^*(x))}^2}} } $ | (9) |
分别用NSGA-Ⅱ、IMOGA算法相同条件下运行20次得到各自的解集, 合并并去除非劣解, 得到非劣解集作为参考集
| 表 1 算法平均性能比较 |
由表1可以看出, 在堆垛机调度问题中, IMOGA算法的
本文对同端出入立体仓库中的堆垛机调度问题进行建模, 针对NSGA-Ⅱ算法容易陷入局部搜索能力不足的问题进行了改进, 并引入了一种局部随机搜索策略来帮助算法跳出局部最优, 提出了一种根据自适应遗传算子和局部搜索策略进行改进后的遗传算法IMOGA. 通过实验分析表明, 在堆垛机调度问题上, IMOGA相较于NSGA-Ⅱ, 不论是解的质量还是收敛速度, 都具有一定的优势, 证明了算法的有效性.
| [1] |
任为. 立体仓库货位优化与仿真研究[硕士学位论文]. 徐州: 中国矿业大学, 2015.
|
| [2] |
韩红艳. 基于Pareto支配的高维多目标进化算法研究[硕士学位论文]. 大连: 大连理工大学, 2016.
|
| [3] |
关榆君, 和淼. 基于猫群算法的立体车库调度优化. 华北理工大学学报:自然科学版, 2018, 40(4): 94-99. |
| [4] |
Deb K, Agrawal S, Pratap A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. Proceedings of the 6th International Conference on Parallel Problem Solving from Nature. France. 2000. 849–858.
|
| [5] |
路艳雪. NSGA-Ⅱ多目标优化算法的改进及应用研究[硕士学位论文]. 太原: 太原理工大学, 2017.
|
| [6] |
魏冰. NSGA-Ⅱ算法的改进及在机组组合优化中的应用[硕士学位论文]. 北京: 华北电力大学, 2019.
|
| [7] |
曲志坚, 张先伟, 曹雁锋, 等. 基于自适应机制的遗传算法研究. 计算机应用研究, 2015, 32(11): 3222-3225, 3229. DOI:10.3969/j.issn.1001-3695.2015.11.004 |
| [8] |
缪朝炜, 苏瑞泽, 张杰. 越库配送车辆调度问题的自适应遗传算法研究. 管理工程学报, 2016, 30(4): 166-172. |
| [9] |
何庆, 吴意乐, 徐同伟. 改进遗传模拟退火算法在TSP优化中的应用. 控制与决策, 2018, 33(2): 219-225. |
| [10] |
Knowles J, Corne D. On metrics for comparing nondominated sets. Proceedings of 2002 Congress on Evolutionary Computation. Honolulu, HI, USA. 2002. 711–716.
|
 2020, Vol. 29
2020, Vol. 29



