2. 云南财经大学 云南省经济社会大数据研究院, 昆明 650221
2. Big Data Research Institute of Yunnan Economy and Society, Yunnan University of Finance and Economics, Kunming 650221, China
当前, 大数据、云计算、区块链等新一代信息技术应用的日益成熟, 正在推动我国数字经济发展进入快车道, 对社会经济发展和人们日常生活产生着重大影响. 数据已经成为政府、企业重要的无形资产和商业应用价值的基点. 在这样的大背景下, 数据资产价值分析和数据资产交易已然成为当前的研究热点和关键点. 数据资产作为政府、企业的一项重要资产, 需要最大化地挖掘数据资产价值, 或是通过运用数据分析以提升政府治理效力和企业竞争力, 或是通过交易变现直接获得资产性收益. 因此, 数据资产的价值评估与交易定价是当前学者们研究的重点领域和方向, 但在很大程度上仍集中在数据资产的确认、会计账目[1,2]等管理层面, 在数据资产计量方面普遍使用目前产业界、学术界基本认可将数据资产纳入“无形资产”的范畴, 并参考现有无形资产的计量方式, 使用重置成本法[3]、收益现值法[4]、市场价值法[5]及综合模型估值法对数据资产进行计量. 其中, 成本法是约束于被评估资产处于继续使用状态或被假定处于使用状态, 应当具备可使用的历史材料, 具有随着时间的推移而陈旧、贬值的特点. 其中, 收益法是把待估剩余经济寿命内数据资产的预期未来收益, 按照一定的贴现率折成现值, 从而确定其价值. 该方法必须满足被评估资产的未来收益可以预测并货币衡量、资产拥有者获得预期收益所承担的风险也可以预测并货币衡量及被评估资产预期获利年限可预测. 其中, 市场法是指将评估对象与可比在线交易数据资产或者可比交易案例进行比较, 确定评估对象价值的评估方法. 其中, 综合估值法是一种综合大数据资产评估方法. 基于数据质量、数据规模、数据内容、行业价值等. 实现数据资产价值计算. 《数据资产价值分析模型与交易体系研究》[6]中提出基于数据资产的颗粒度、多维度、规模度、活性度和关联度等5个特征维度和基于深度学习的数据资产价值分析框架和方法.
就目前形势而言, 数据资产的每年预期收益很难得到较为一致且准确的认同, 故收益法应用于数据资产价值评估就目前而言比较困难. 而随着深度整合挖掘的数据资产价值升值亦不符合成本法的使用前提. 综合法虽然综合考虑了数据资产特征等按质估值, 利用了深度学习等前沿技术, 但解释性及透明度欠佳. 于此, 随着大数据交易所陆续成立、发展壮大, 数据资产交易市场领域细分越来越充分且透明, 市场法应是数据资产价值评估的首选.
直观的, 数据越重要, 其价值也越高. 数据交易越频繁, 其数据价值越高. 则可映射为数据资产估值取决于数据资产的初始估值和数据资产交易的频率. 数据资产的初始价值可以通过爬取同类数据资产信息建立数据资产库, 选取和确定比较数据资产, 分析比较可比在线交易数据资产和待估对象, 选取比较参数和指标, 并确定比较体系, 对数据资产市值加权平均得到. 数据资产交易频率可以通过在线交易平台取得. 因此, 构建基于数据资产初始估值和交易频率的数据资产估值计量模型是研究的难点和关键.
在狭义相对论中的质速关系[7]中, 从洛伦兹变换中可以得到如下质速关系公式, 如式(1)所示.
| $ m = \dfrac{{m_0}}{{\sqrt {1 - {{\left( {\dfrac{v}{c}} \right)}^2}} }} $ | (1) |
式(1)中表明, 物体的惯性质量并不是一个不变的常数, 它会随着速度v的加快而变大. 当物体速度v趋于光速c时, 原来静止质量m0的物体, 运动质量m会增加到无穷大. 洛伦兹变换简单可靠, 且理论基础坚实, 已经广泛的应用于物理、生物、工程等高新技术领域, 学者们对此也进行了大量的跨学科的研究工作. 例如文献[8,9]就狭义相对论洛伦兹变换的推导及其他进行了深入研究, 也为数据资产的估值研究提供了一些重要参考和依据.
在此我们将数据资产估值与物体的惯性质量进行类比, 将数据资产初始估值与原本静质量m0进行类比, 数据资产交易频率与物体速度进行类比. 于此, 本文以洛伦兹变换作为理论基础研究数据资产估值的计量方法.
众所周知, PageRank算法[10-12]是经典的基于链接的Web页面排序算法. 近年来, 许多学者将该算法用于微博用户影响力的研究中, 例如, 文献[10]基于PageRank算法的思想, 提出了一种基于标签化的PageRank重要微博用户推荐算法; 文献[11]也是以PageRank算法作为理论依据, 用PageRank值实现用户价值的重要程度的度量; 文献[12]通过PageRank算法确定多齐次映射的特征向量, 以PageRank值度量时域网络中心节点.
借鉴PageRank算法中基于网页的“链接关系”来计算网页价值影响力的方法, 本文将数据资产与网页页面进行类比, 将数据资产之间的市场相互参价关系与PageRank模型中的前向和反向链接进行类比, 利用数据资产相互的“参价”关系, 基于PageRank算法计算其在数据资产参价体系中的重要程度, 并以此作为数据资产计算的权重系数.
综上, 本文将采用市场法并结合洛伦兹变换和PageRank算法对数据资产进行估值计算. 其具体思路如下: 以数据资产的初始估值计量为出发点, 以后续数据资产计量为研究重点. 首先确定数据资产的估值特征, 编写代码抓取数据资产实例以获取数据资产市场价格及交易频率, 应用PageRank算法得到数据资产权重系数, 确认数据资产初始估值. 然后再利用洛伦兹变换, 最终得到数据资产后续估值.
1 问题陈述假设数据资产d的状态估值(待估数据资产的估值)为da和数据资产d的初始估值da0的关系用D(da0,r)表示, 则其之间关系可以描述为:
| $ D\left( {{d_{a0}},r} \right) = {d_{a0}} \times \left( {1 + r} \right) $ | (2) |
其中, r为数据资产重要程度的估值系数, 且
(1)对于D, 如在狭义相对论中洛伦兹变换, 描述参照第1节中式(1)所示. 我们将数据资产估值与物体的惯性质量进行类比, 将数据资产初始估计与原本静质量进行类比, 数据资产交易频率与物体速度进行类比. 因此, 本文以洛伦兹变换作为研究数据资产估值的计量方法的支撑理论基础, 在本文第2节将就此重点展开.
| $ {D_a} = \dfrac{{{d_{a0}}}}{{\sqrt {1 - {{\left( {\dfrac{{c - v}}{c}} \right)}^2}} }}\left( {1 + r} \right) $ | (3) |
对于da0, 应用市场法计量, 其数据资产初始估值的基本模型为:
| $ {d_{a0}} = \dfrac{{\left( {\displaystyle\sum\limits_{i = 1}^n {{p_i} \times {w_i}} } \right)}}{n} $ | (4) |
其中, da0: 被评估数据资产价值; pi: 第 i个可参照数据资产的基准价值(p).
wi: 修正系数.
(2)对于r, 我们采用PageRank算法来衡量数据资产估值的重要程度, 并计算得到数据资产的估值系数. 我们以PageRank算法作为理论依据, 提出如下2点假设:
假设1. 以数据资产相互参价的“链接”关系, 用数据资产的PageRank值表示其估值程度.
假设2. 数据资产的交易对手类型越重要, 说明其估值就越高.
于此, 具体计算方法可以描述如下:
| $ R({d_a}) = {\left( {(1 - d) + d\sum\limits_{i = 1}^n {\dfrac{{P({d_i}) \times {U_i}}}{{C({d_i})}}} } \right)^*} $ | (5) |
其中, da表示一个数据资产, 有n个数据资产(d1, d2, ···, dn)参价da的估值; P(da)表示数据资产da的PageRank值, 存在数据资产di参价数据资产da的估值, P(di)为数据资产di的PageRank值; C(di)为从数据资产di参价其他数据资产的次数; d为阻尼系数, 通常取值在(0, 1)之间, 表示数据资产di参价数据资产da估值的概率. Ui为购买数据资产的交易对手对应的重要程度并归一化, 通常取值在(0, 1)之间, 初始值设为0.5.
下面通过一个简单的例子来说明基于式(5)计算数据资产重要程度的方法. 假设存在数据资产du和dv(这里仅考虑2个数据资产的情形), 其中数据资产du被数据资产dv参价的次数为10, 即C(dv)=10. 鉴于计算的方便, 我们设定R(dv)值为1, 阻尼系数取0.85计算, 通过式(5), 得到R(u)=((1−0.85)+0.85×(1/10))×0.5=0.118.
2 数据资产估值根据第2节给出的方法, 可以得到数据资产的初始估值、数据资产重要程度系数及数据资产状态估值.
2.1 数据资产的初始估值计量对于数据资产的初始估值计量技术路线分为3个步骤. 首先确定数据资产特征维度并量化, 然后设计数据资产估值分析模型, 最后计算得到数据资产估值.
(1)数据资产特征维度
采用市场法对待估数据资产进行估值, 需要将待评估资产和可比的在线交易数据资产进行两两比较, 前提是需要对数据资产的可量化特征进行选取, 继而通过比较确定待估数据资产的相对价值系数.
在数据资产特征选择上, 借鉴文献[13]的研究成果, 并考虑到特征获取的难易程度和计算量, 我们通过应用模糊层次分析法, 计算指标影响因子权重, 继而对数据资产的代表特征进行筛选.
第1步. 确立数据资产特征及评语集
数据资产特征为: {交易对手类型、颗粒度、多维度、活性度、规模度、关联度、用户评价、交易商、交易价格}等9个指标, 评语集为: V={5,4,3,2,1}, 按重要性高低排序. 详见表1.
第2步. 构造优先关系矩阵, 并改造为模糊一致矩阵.
首先构建优先关系矩阵, 然后再将关系优先矩阵改造为模糊一致矩阵. 在模糊层次分析中, 优先关系矩阵是每一层中指标对上一层指标的相对重要程度两两比较建立的模糊互补矩阵, 表示为:
各特征权重计算:
| $ {{W}}_i = \dfrac{1}{n} - \dfrac{1}{{2a}} + \dfrac{1}{{na}}\sum\limits_{j = 1}^n {a_{ij}};\;\;i = 1,2,\cdots,n,\;a \ge \dfrac{{n - 1}}{2} $ | (6) |
第3步. 计算各指标权重
求解A-B 优先关系矩阵以及A-B模糊一致矩阵, 数据资产特征权重依次为:
| $ {W}_{{\rm{1 - 9}}} = \left( {0.05,0.11,0.15,0.25,0.14,0.11,0.1,0.04,0.05} \right) $ |
择取特征权重前5个特征作为模型输入指标, 并归一化, 详见表2.
| 表 1 数据资产评价特征表 |
| 表 2 数据资产特征及权重归一化表 |
(2)数据资产估值分析模型
基于式(4)数据资产初始估值模型和表1提出的特征维度及权重, 提出估值模型的进一步细化.
| $ {d_{a0}} = \dfrac{{\left( {\displaystyle\sum\limits_{i = 1}^n {{p_i} \times {{\left( {\sum {\left( {\alpha + \beta + \gamma + \delta + \lambda } \right)} } \right)}_i}} } \right)}}{n} $ | (7) |
其中, da0为被评估数据资产初始估值; pi为第i个可参照数据资产的基准估值; wi为修正系数. n≥3, 具体可参照数据资产的数量不少于3个.
(3)计算数据资产初始估值
① 假设有一数据资产i需上市交易, 其初始估值设为di.
② 通过网络抓取技术, 建立数据资产i的可比数据资产价值结构化实例库, 然后通过专家打分法确定特征维度的权重系数. 为避免专家打分过强主观, 实验采用2组专家分别交叉打分, 并对结果进行一致性检验. 经Kappa检验, 得到Kappa值为0.763, 说明对于特征的权重一致性较好. 对于特征权重取值为分组打分的均值, 结果如表3所示.
| 表 3 数据资产在线交易实例样表 |
③ 合成初步估值结果
根据式(6)进行数据资产价值评估计量, 并货币化. 计算过程如下:
| $\begin{split} da0 = &(\left( {1.00 \times \left( {0.2 + 0.2 + 0.18 + 0.15 + 0.2} \right)} \right) +\\ & 0.85 \times \left( {0.2 + 0.2 + 0.19 + 0.2 + 0.2} \right)+\\ & \left( {0.78 \times \left( {0.2 + 0.2 + 0.2 + 0.2 + 0.15} \right)} \right)/3 = 0.84 \end{split}$ |
首先假设存在数据资产参价行为, 且假定存在交易对手, 即数据购买者. 其类型的分为个人、企业, 其权重系数分别设置为0.5, 0.8. 其属性值如表4所示.
| 表 4 数据资产参价对属性列表 |
根据第2节式(5), 计算步骤如下:
| $ \begin{split} R(it) = & ( 1 - 0.85) + 0.85\times(( 1/5\times0.8 ) + ( 0.85/8\times0.5 ) +\\ & (0.78/6\times0.5)) = 0.39 \end{split} $ |
根据3.1、3.2节得到的结果及式(3), 假设数据资产i的交易频率(v)为7日/次, 标准交易频率(c)为30日/次, 则可计算得到数据资产i的估值. 计算步骤如下:
| $ D\left( i \right) = 0.84/{\rm{SQRT}}\left( {1 - {{\left( {\left( {30 - 7} \right)/30} \right)}^2}} \right)\times\left( {1 + 0.39} \right) = 1.85 $ |
为了验证本文所提出方法的可行性和有效性, 我们编程实现了本文提出的基于洛伦兹变换和PageRank算法的数据资产估值的方法, 并进行了实验测试和分析. 我们从贵阳数据交易所、神气气象数据交易平台及数据宝等在线数据交易平台抽取的数据资产库, 共有10 257条记录作为实验数据, 主要包括数据资产编号、数据资产名称、数据类型、交易量、交易价格等信息.
实验环境如下: Windows 10 Professional 操作系统, Intel(R) Xeon(R) CPU E5-2650 v4 2.2 GHz (2核CPU), 16 GB 内存. 使用Python编程语言编写程序, 使用MySQL存储实验数据资产等数据.
我们测试了数据资产估值计算的效率, 执行时间包括数据库连接时间、查询数据库及估值计算时间.
图1给出了随着数据资产算例的逐渐增加执行时间变化趋势. 可以看出数据资产估值的计算时间随着参照算例的增加基本呈线性趋势增长态势, 可以说执行时间对数据资产算例数量不敏感, 这说明本文提出的计算方法是高效的.

|
图 1 随着数据资产数量增加的执行时间变化趋势 |
同时, 我们为了测试本文所提出方法的准确性, 我们借鉴统计学领域中的MAE (平均绝对误差)和RMSE (均方根误差)[14]这两个常用度量指标来测试本文方法的有效性. 其中MAE为实验中计算得到的数据资产估值与人工观测值之间绝对误差的平均值. MAE越小越好. MSE为实验中计算得到的数据资产估值与和人工观测值之间差异的样本标准偏差, 说明样本的离散程度. 做非线性拟合时, RMSE越小越好. 于此, 我们事先对10个待估数据资产实例进行了的人工判断和估值定价, 并以此作为估值有效性的判断标准.
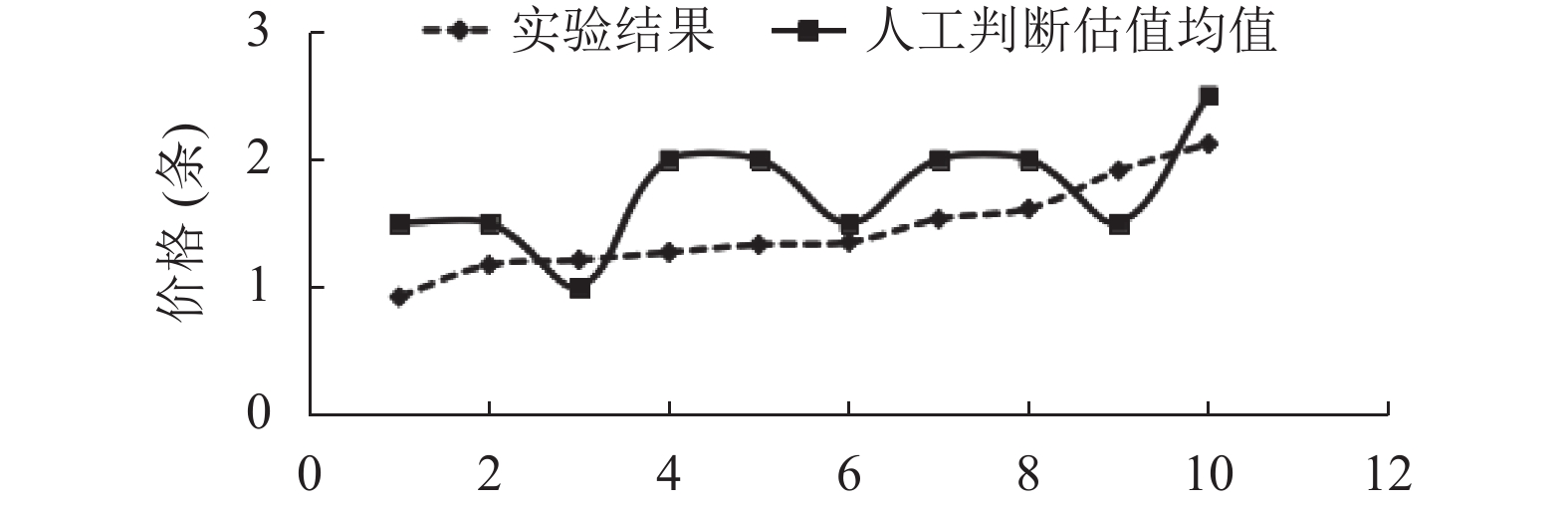
基于本文提出的方法计算得到的数据资产实验结果与人工观测评估的MAE值为0.4320, RMSE值为0.4668, 这从一定程度上说明了本文所提出方法的有效性. 其数据资产实验计算估值与人工估值比对图结果如图2所示.
为避免人工估值带来的主观误差, 进一步验证模型的有效性. 我们在市场中抓取与上述10个待估数据资产实例相似度较高的数据交易资产的价格作为参照标的, 进行MAE和RMSE分析. 通过计算得到MAE值为0.4618, RMSE值为0.5319, 与人工估值对比波动范围在6~13%之间, 如图3所示.
|
图 2 数据资产实验计算估值与人工估值比对图 |

|
图 3 数据资产实验计算估值与市场价格比对图 |
4 总结展望
本文针对数据资产估值的问题, 提出了基于洛伦兹变换和PageRank算法的计算方法. 我们依据洛伦兹变换原理将数据资产的估值与物体的惯性质量进行类比, 将数据资产初始估计与原本静质量进行类比, 数据资产交易频率与物体速度进行类比, 提出计算数据资产状态估值的计算方法. 我们采用PageRank算法来确定数据资产估值之间的依赖程度, 并以此计算得到数据资产的估值系数. 我们应用市场法并借鉴目前公允的层次计量模型计算数据资产初始估值, 最终给出了数据资产状态估值的计算方法. 并通过实验测试了方法的效率、稳定性和有效性. 不可否认, 数据资产的估值与计量是一项复杂的系统工程, 如何进一步提高数据资产的重要程度计算, 如何避免数据交易品种的差异带来的交易频率及标准频率变换而导致估值的不可控性以及如何更加科学的确认数据初始估值的算法以提高数据资产初始估值精度, 将是目前我们将进一步要开展的重要研究工作.
| [1] |
徐漪. 大数据的资产属性与价值评估. 产业与科技论坛, 2017, 16(2): 97-99. DOI:10.3969/j.issn.1673-5641.2017.02.051 |
| [2] |
邹照菊. 关于大数据资产计价的若干思考. 财会通讯, 2018(28): 35-39. DOI:10.16144/j.cnki.issn1002-8072.2018.28.009 |
| [3] |
Kozyr YV. Business valuation based on assets replacement cost. Journal of Finance and Investment Analysis, 2014, 3(3): 1-12. |
| [4] |
Lagrost C, Martin D, Dubois C, et al. Intellectual property valuation: How to approach the selection of an appropriate valuation method. Journal of Intellectual Capital, 2010, 11(4): 481-503. DOI:10.1108/14691931011085641 |
| [5] |
Gao Y, Lim KG, Ng KH. An approximation pricing algorithm in an incomplete market: A differential geometric approach. Finance and Stochastics, 2014, 8(4): 501-523. |
| [6] |
张驰. 数据资产价值分析模型与交易体系研究[博士学位论文]. 北京: 北京交通大学, 2018.
|
| [7] |
戴又善, 戴亮. 普遍的质速关系和狭义相对论. 北京大学学报(自然科学版), 2014, 50(3): 403-410. DOI:10.13209/j.0479-8023.2014.063 |
| [8] |
Qin XP, Li P, Su G, et al. Derivation of Lorentz transformation via Lorentz invariant. Proceedings of the 2nd International Conference on Automatic Control and Information Engineering. Beijing, China. 2017. 50–53.
|
| [9] |
张元仲. 狭义相对论洛伦兹变换的推导及其他. 物理与工程, 2016, 26(3): 3-8. DOI:10.3969/j.issn.1009-7104.2016.03.001 |
| [10] |
王嵘冰, 安维凯, 冯勇, 等. 基于标签和PageRank的重要微博用户推荐算法. 计算机科学, 2018, 45(2): 276-279. DOI:10.11896/j.issn.1002-137X.2018.02.047 |
| [11] |
赵小明, 张群, 岳昆. 基于静电场理论和PageRank算法的微博用户相关性分析. 云南大学学报(自然科学版), 2015, 37(2): 207-214. DOI:10.7540/j.ynu.20140430 |
| [12] |
Lv LS, Zhang K, Zhang T, et al. PageRank centrality for temporal networks. Physics Letters A, 2019, 383(12): 1215-1222. DOI:10.1016/j.physleta.2019.01.041 |
| [13] |
李伟霖, 王成良, 文俊浩. 基于评论与评分的协同过滤算法. 计算机应用研究, 2017, 34(2): 361-364, 412. DOI:10.3969/j.issn.1001-3695.2017.02.009 |
| [14] |
呼亚杰. 一种基于类别偏好协同过滤推荐算法的实现与优化[硕士学位论文]. 兰州: 兰州大学, 2016.
|
 2020, Vol. 29
2020, Vol. 29


