由于互联网不断产生大量视频、音频、文章等, 人们很难有效地找到自己喜欢的事物, 个性化推荐系统能够帮助人们快速从大量信息中作出选择、提供建议、辅助决策^[1]. 阿里, 京东等公司通过使用推荐系统吸引了大量的用户, 并通过推荐系统提供的个性化服务, 创造了惊人的销售业绩.

个性化推荐、基于内容的推荐和基于知识的推荐已经得到了广泛应用, 其中协同过滤(CF)是推荐系统中最突出、最流行的技术之一^[2]. 协同过滤算法一般分为基于邻域的协同过滤和基于模型的协同过滤. 基于模型的协同过滤, 通过使用大量数据来训练模型, 然后使用该模型预测用户的偏好. 加权λ正则化的交替最小二乘法(ALS-WR)是基于模型的CF的一个经典案例, ALS-WR是基于矩阵因子分解算法实现的, 并且能够很好地解决数据的稀疏性和可扩展性问题^[3].

基于模型的CF在提高预测精度以及应对数据稀疏性方面优势明显. 但它有一些缺点, 如构建模型的成本很高^[2]. 基于邻域的CF不需要构建特定的模型, 而是使用用户评分矩阵来计算用户或项目之间的相似性. 因此, 基于邻域的CF实现起来更容易. 但是, 它也有一些缺点, 如十分依赖用户的评分、当数据很稀疏时预测精度急剧下降以及无法为新用户进行推荐^[2]. 基于邻域的CF算法又分为基于用户的CF和基于项目的CF. 基于用户的CF和基于项目的CF算法的本质是根据评分计算用户相似性和项目相似性, 在找到相似的用户(称为邻居)后, 基于用户的CF将邻居们最喜爱而自己不熟悉的前N个项目进行推荐. 当用户数量远远大于项目数量时, 基于用户的CF可扩展性较差. 不少学者曾尝试使用基于项目的CF来解决可扩展性问题, 但是当用户和项目的数量很大时, 仍然不能完全解决这个问题. 尽管CF有这些不足, 但它仍然是最具代表性的推荐算法.

文献[4]在致力于降低平均绝对误差(MAE)或均方根误差(RMSE)方面, 对CF算法进行了大量的研究. 然而, 对推荐系统来说仅靠降低MAE或RMSE数值, 并不能从本质上提高推荐的准确性. 假设两个推荐系统具有相同的评分预测MAE或RMSE. 值得注意的是它们在用户体验(UX)方面可能不同, 因为一个推荐系统可能推荐一个项目, 而另一个推荐系统没有推荐该项目. 针对上述不足, 与用户体验相关的性能指标, 如查准率、召回率和F1-score得到了广泛应用.

潘多拉互联网电台、Netflix和Artsy基于聚类的推荐算法分别开发了音乐基因组项目、微电影和艺术基因组项目. 这些基于聚类的推荐算法取得了令人满意的效果, 但是聚类的处理成本很高. 例如, 就音乐基因组项目而言, 音乐家分析每首歌曲的过程通常需要20到30分钟.

综上所述, 基于邻域的协同过滤算法存在数据稀疏性以及冷启动问题, 基于模型的协同过滤算法在提高预测精度以及应对数据稀疏性方面优势明显, 但构建模型的成本很高. Netflix、Artsy基于聚类的推荐算法取得了令人满意的效果, 因此本文采用聚类的推荐算法, 针对聚类的处理成本较高, 本文设计了一种处理成本低、只需要用户给出评分, 简单易于实现的聚类的算法; 为了提高推荐准确率, 根据实际评分数据和皮尔逊相关系数, 将用户分为若干用户簇, 并深入研究了用户与用户簇之间的偏好的差异, 根据同一用户簇中用户的偏好倾向, 对每个项目进行激励/惩罚, 即本文通过使用激励/惩罚用户模型(IPU)的CBCF算法, 在准确率、召回率和F1-score方面来提高推荐系统的性能.

1 相关研究

本文提出的算法涉及推荐系统中的CF算法、聚类算法、基于聚类的推荐系统等研究领域, 对推荐系统的性能指标诸如准确率和召回率等进行了研究分析, 并总结了基于CF算法的偏好预测以及两种聚类算法.

1.1 CF算法

CF是推荐系统最常用的技术之一, 但在数据稀疏和冷启动等方面存在不足^[5]. 如果用户评分矩阵过于稀疏, 那么预测评分就会不准确. 此外, CF很难对新用户或项目进行预测评分. 解决这两个问题有很大的挑战^[6]. 文献[4]在如何提高CF推荐系统的预测精度上进行了研究.

1.2 聚类算法

聚类已广泛应用于各种数据挖掘应用: 如K-means以及文献[7]提出的监控游戏粘性DBSCAN聚类算法. 文献[8]提出了一种新的基于熵的目标函数来聚类不同类型的图片. 为了满足并行处理系统的实时性要求, 文献[9]中提出了一种改进的一维数据均值聚类算法.

1.3 基于聚类的推荐系统

文献[10–12]在通过聚类算法提高推荐的准确性方面进行了深入研究. 文献[10]中, CF和基于内容的推荐分别用于查找相似的用户和项目, 并进行聚类, 然后对目标用户进行个性化推荐. 结果表明在准确率、召回率和F1 score方面的表现有所改善. 文献[11]提出对每组数据进行矩阵分解之前先进行聚类处理. 文献[12]对使用K-means、自组织映射(SOM)和模糊C均值(FCM)聚类算法应用于基于用户CF的性能进行研究. 结果表明, 与K均值和SOM聚类算法相比, 使用FCM聚类算法的基于用户的CF具有更好的性能.

1.4 性能指标分析及偏好预测方法

文献[13]研究了广泛应用于评价推荐系统优劣的性能指标, 如准确率、召回率和F1-score等. 使用CF进行偏好预测的算法分为基于邻域的推荐算法和基于模型的推荐算法. 基于邻域的推荐算法直接利用大量历史数据来预测目标项目的评分, 并为活跃用户进行推荐. 基于邻域的推荐算法进行推荐过程中需要将所有数据加载到内存中, 并在数据上实现特定的算法. 基于模型的推荐算法通过基于已知数据利用数据挖掘的方法来建立预测模型, 建立好预测模型后, 在推荐过程中就不再需要历史数据了^[14].

本文研究了基于邻域的CBCF算法, 尽管基于模型的方法在预测速度和可扩展性方面具有优势, 但在灵活性和预测质量等方面存在不足, 建立模型通常是一个耗费时间和资源的过程, 建立模型的方式对预测质量的影响较大.

1.5 聚类

在SOM、K-means、FCM和谱聚类等聚类算法中, 本文选择了谱聚类和FCM聚类算法, 因为这两种算法能取得令人满意的效果. 下面简单阐述一下这两种算法.

谱聚类使用了关联矩阵的特征向量来进行聚类. 两个对象之间的相似度越高, 这两个对象之间的关联值越大. 高斯相似度函数用于计算两个对象之间的相似度, 常用于构造关联矩阵, 高斯相似函数 $s(x_i,x_j) = e\dfrac{{ - ||x_i - x_j|{|^2}}}{{2{\sigma ^2}}}$ . 其中, σ控制邻居范围的大小^[15]. 得到关联矩阵后, 对关联矩阵的特征向量来进行聚类, 最后谱聚类根据特征向量来进行聚类. 谱聚类实现简单, 可以通过标准的线性代数软件进行求解, 而且效果明显也优于传统的聚类算法(如K-means 算法)^[15].

FCM聚类^[16]通过系数 $w_{ij}^m$ 将对象 ${x_i}$ 划分到簇 ${c_j}$ , 使每个对象成为具有不同模糊隶属度的所有聚类的成员, 其中m是控制集群模糊程度的超参数. m越大, 簇越模糊. FCM聚类首先在给定多个聚类的情况下随机初始化每个聚类的中心点. 然后, 重复以下两个步骤直到两次迭代之间系数的变化小于给定的阈值. (1)计算每个簇的质心; (2)计算每个点在簇中的系数.

2 基于聚类和奖惩用户模型的推荐算法 2.1 问题定义

本文的创新在于当MAE或RMSE相同的情况下, 可以做出是否推荐某个项目的正确决策, 来提升用户体验. 例如, 假设用户A对项目B的实际评分为4.2, 两个推荐系统分别预测用户A对项目B的评分偏好为3.8和4.6. 预测评分大于4.0的项目将推荐给用户, 这两个推荐系统的MAE是相同的, 但只有后一个系统会推荐该项目. 为了提升用户体验, 本文根据用户的偏好倾向对每一个项目进行激励或惩罚. 为此, 将用户分为若干簇, 并根据用户所属的簇的情况来决定对项目的奖惩.

图1显示了使用IPU模型的CBCF算法的示例, 假设有2个项目和4个用户簇, 假设用户被分成4个簇, 即C₁、C₂、C₃和C₄. 从图1可以看出, 用户u1、u2、u6和u17属于簇C₁. 其中, 实心方形项目和实心圆形项目分别表示测试数据和训练数据. ${\mathop r\limits^ {\wedge}} _{u,i}$ 和 $r_{u,i}$ 分别为用户u对项目i的预测评分和实际评分, 其中基于邻域的CF和基于模型的CF可用于评分预测. 如图1所示, 用户17对项目1实际的评分 $r_{u17,i1} = 4.0$ 及其预测的评分 ${\mathop r\limits^{ \wedge}} _{u17,i1} = 3.9$ . 用户u已经评分的项目用红色实心表示, 没有评分的项目用空心表示. 例如, 在簇C₁中, 用户u1、u2和u17对i1的评分分别为5.0、5.0和4.0, 即 $r_{u1,i1} = 5.0$ 、 $r_{u2,i1} = 5.0$ 和 $r_{u17,i1} = 4.0$ . 用户u1、u2和u6对i2的评分分别为5.0、4.0和3.0, 即 $r_{u1,i2} = 5.0$ 、 $r_{u2,i2} = 4.0$ 和 $r_{u6,i2} = 3.0$ . ${\overline{ C}}_c^i$ 表示为用户簇 $Cc$ 中用户对项目i的平均偏好. ${\overline{ C}}_c^i$ 可以表示为:

${\displaystyle {\overline{ C}}_c^i} = \frac{{\displaystyle\sum\nolimits_{u \in U_{i,c}} {r_{u,i}} }}{{|U_{i,c}|}}$

(1)

其中, $U_{i,c}$ 是用户簇 $C_c$ 中对项目i进行评分的一组用户. 如图1所示, 用户簇C1对 $i1$ 的平均偏好 ${\overline{ C}}_1^{i1}$ 为4.67.

根据每个用户簇 ${\overline{ C}}_c^i$ , 使用IPU模型来决定某个项目是否推荐给用户u. 具体推荐策略为, 当 ${\overline{ C}}_c^i$ 的值足够大时, 即 ${\overline{ C}}_c^i \ge \gamma$ , 给予项目i激励, 其中γ>0表示待优化的参数. 当 ${\overline{ C}}_c^i < \gamma$ , 给予项目i惩罚, 系统参数α和β分别用作惩罚和激励的阈值, 并设置为正数, 其中 $\alpha \ge \beta $ . 例如, 假设α=4.5, β=3.5, γ=3.0. 在图1中, i1将被推荐给u19, 但如果i1和i2(即 ${\mathop r\limits^ {\wedge}} _{u19,i1}$ 和 ${\mathop r\limits^ {\wedge}} _{u19,i2}$ )的预测偏好分别为3.8和4.2, 则i2将不被推荐给u19. 因为 ${\overline{ C}} _3^{i1}( = 4.33)$ 大于 $\gamma ( = 3.0)$ , ${\mathop r\limits^ {\wedge}} _{u19,i1}( = 3.8)$ 也大于 $\beta ( = 3.5)$ 然而, 在i2的情况下,u19不被推荐, 因为 ${\overline{ C}} _3^{i2}( = 2.33)$ 小于γ, ${\mathop r\limits^ {\wedge}} _{u19,i2} < \alpha $ . 简而言之, 根据用户簇获得的偏好倾向来改变推荐决策.

算法1. 使用IPU模型的CBCF算法

1.　if $\scriptstyle{\overline{ C}} _c^i \ge \gamma$ then

2.　　if $\scriptstyle{\mathop r\limits^ {\wedge}} _{u,i} \ge \beta$ then

3.　　　将项目i推荐给用户u

4.　　else 项目i不被推荐

5.　else

6.　　if $\scriptstyle{\mathop r\limits^ {\wedge}} _{u,i} \ge \alpha$ then

7.　　　将项目i推荐给用户u

8.　　　else 项目i不被推荐

9.　end

算法1描述了使用IPU模型CBCF算法, 从算法1中可以看出, 当 ${\overline{ C}} _c^i \ge \gamma$ , 时, 只有当预测评分大于β才进行推荐. 如果 ${\overline{ C}} _c^i < \gamma$ ,, 则仅当预测评分大于α才进行推荐.

如前所述, 准确率、召回率和F1-score作为性能评估的指标, 这3个性能指标可以表示为真正类(TP)、真负类(TN)、假正类(FP)和假负类(FN)的函数. 假设预测条件为真. 如果条件实际为真(或假), 则为TP (或FP), 假设预测条件为假, 如果条件实际上为真(或假), 则为FN (或TN). 对于给定的用户u和项目i, TP、TN、FP和FN依赖于α、β和γ, 因此:

$\left\{ \begin{split} & f_{\rm TP}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}) = I_{[\gamma ,\infty )}({\overline{C}} _c^{u,i}) \cdot I_{[\beta ,\infty )}({\hat{r}} _{u,i}) \cdot I_{[\delta _{\rm pref},\infty )}(r_{u,i}) + I_{(0,\gamma )}({\overline{C}} _c^{u,i}) \cdot I_{[\alpha ,\infty )}({\hat{r}} _{u,i}) \cdot I_{[\delta _{\rm pref},\infty )}(r_{u,i}) \\ & f_{\rm FP}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}) = I_{[\gamma ,\infty )}({\overline {C}} _c^{u,i}) \cdot I_{[\beta ,\infty )}({\hat{r}} _{u,i}) \cdot I_{(0,\delta _{\rm pref})}(r_{u,i}) + I_{(0,\gamma )}{\overline{C}} _c^{u,i}) \cdot I_{[\alpha ,\infty )}({\hat{r}} _{u,i}) \cdot I_{(0,\delta _{\rm pref})}(r_{u,i}) \\ & f_{\rm FN}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}) = I_{[\gamma ,\infty )}({\overline{C}} _c^{u,i}) \cdot I_{(0,\beta )}({\hat{r}} _{u,i}) \cdot I_{[\delta _{\rm pref},\infty )}(r_{u,i}) + I_{(0,\gamma )}({\overline{C}} _c^{u,i}) \cdot I_{(0,\alpha )}({\hat{r}} _{u,i}) \cdot I_{[\delta _{pref},\infty )}(r_{u,i}) \\ & f_{\rm TN}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}) = I_{[\gamma ,\infty )}({\overline{C}} _c^{u,i}) \cdot I_{(0,\beta )}({\hat{r}} _{u,i}) \cdot I_{(0,\delta _{pref})}(r_{u,i})+ I_{(0,\gamma )}({\overline{C}} _c^{u,i}) \cdot I_{(0,\alpha )}({\hat{r}} _{u,i}) \cdot I_{(0,\delta _{pref})}(r_{u,i}) \end{split} \right.$

(2)

其中, IA(x) 是集合A函数, δ_pref是确定用户是否真正喜欢相应项目的阈值, 其中δ_pref通常设置为4.0 (用户评分满分为5.0)或8.0 (用户评分满分为10.0). 如果 ${\overline{ C}} _c^{u,i} \ge \gamma$ , ${\hat{ r}} _{u,i} \ge \beta$ , ${r} _{u,i} \ge \delta _{\rm pref}$ 则 $f_{\rm TP}^{u,i} = 1$ ; 如果 ${\overline{ C}} _c^{u,i} < \gamma$ , ${\hat{ r}} _{u,i} \ge \alpha$ , ${r} _{u,i} \ge \delta _{\rm pref}$ 则 $f_{\rm TP}^{u,i} = 1$ ; 反之 $f_{\rm TP}^{u,i} = 0$ . 类似的, 如果 ${\overline{ C}} _c^{u,i} \ge \gamma$ , ${\hat{ r}} _{u,i} \ge \beta$ , ${r} _{u,i} < \delta _{\rm pref}$ 则 $f_{\rm FP}^{u,i} = 1$ ; 如果 ${\overline {C}} _c^{u,i} < \gamma$ , ${\hat{ r}} _{u,i} \ge \alpha$ , ${r} _{u,i} < \delta _{\rm pref}$ 则 $f_{\rm FP}^{u,i} = 1$ , 反之 $f_{\rm FP}^{u,i} = 0$ 而且, 如果 ${\overline{ C}} _c^{u,i} \ge \gamma$ , ${\hat{ r}} _{u,i} < \beta$ , ${r} _{u,i} \ge \delta _{\rm pref}$ 则 $f_{\rm FN}^{u,i} = 1$ ; 如果 ${\overline{ C}} _c^{u,i} < \gamma$ , ${\hat{r}} _{u,i} < \alpha$ , ${r} _{u,i} \ge \delta _{\rm pref}$ 则 $f_{\rm FN}^{u,i} = 1$ ; 反之 $f_{\rm FN}^{u,i} = 0$ . $f_{\rm TN}^{u,i}$ 的计算方法与上述方法类似. 基于式(2), 准确率和召回率为:

$ \left\{ \begin{split} & precision(\alpha ,\beta ,\gamma ,\delta _{\rm pref}) = \frac{{\displaystyle\sum\nolimits_{(u,i) \in T} {f_{\rm TP}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}} )}}{{\displaystyle\sum\nolimits_{(u,i) \in T} {f_{\rm TP}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}} ) + \displaystyle\sum\nolimits_{(u,i) \in T} {f_{\rm FP}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}} )}}\\ &recall(\alpha ,\beta ,\gamma ,\delta _{\rm pref}) = \frac{{\displaystyle\sum\nolimits_{(u,i) \in T} {f_{\rm TP}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}} )}}{{\displaystyle\sum\nolimits_{(u,i) \in T} {f_{\rm TP}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}} ) + \displaystyle\sum\nolimits_{(u,i) \in T} {f_{\rm FN}^{u,i}(\alpha ,\beta ,\gamma ,\delta _{\rm pref}} )}} \end{split}\right. $

(3)

其中, T表示用于计算准确率和召回率的测试数据集. F1-score 计算公式如下:

$F_1(\alpha ,\beta ,\gamma ,\delta _{\rm pref}) = \frac{{2precision \times recall}}{{precision + recall}}$

(4)

回顾图1中的例子, 其中α=4.5, β=3.5, γ=3.0. 实心方形项目表示测试数据. 假设评分超过4星的项目是用户所感兴趣的, 即 $\delta _{\rm pref} = 4.0$ , 是推荐系统中的一个典型假设^[17]. 那么, 项目i1应该推荐给用户u17, 而不能推荐给用户u8. 用户u29和u8实际上对项目i2很感兴趣. 根据图1中的测试数据集, TP、TN、FP和FN总结在表1中. 本文将不使用聚类算法的CF与本文提出的算法进行比较, 为此, 假设γ=0, 并修改推荐策略, 只有当预测的偏好 ${\hat{ r}} _u^i$ 不小于4.0时, 才推荐项目i. 表1中描述了TP、TN、FP和FN, 从表1可知, 当γ=0时, u4对项目i1感兴趣, u6、u8对项目i2感兴趣, 当γ=3.0时, u17、u4对项目i1感兴趣, u6、u29、u8对项目i2感兴趣, 即u17实际上对项目i1很感兴趣, u29实际上对项目i2很感兴趣. 利用表1的结果, 本文计算γ=0和γ=3.0 这两种情况的准确率和召回率, 如表1所示.

(1) γ=0(不使用聚类的CF算法): 从表1可以看出, TP=2, FP=1, FN=3. 因此, 使用式(3)计算准确率为2/3, 召回率为2/5.

(2) γ=3.0(本文提出的算法): 假设 $\alpha $ =4.5且 $\beta $ =3.5. 从表1可以得出, TP=4, FP=1, FN=1, 使用式(3)计算准确率为4/5, 召回率为4/5.

因此, 当用户分为多个簇, 使用IPU模型, 并适当调整系统参数α、β和γ, 可以显著地提高准确率和召回率.

2.2 公式化

值得注意的是, 准确率、召回率和F1-score随α、β和γ的变化而变化. 因此, 本文的目标是找到最优值α、β和γ, 从而最大化F1-score(或召回率). 因此, 本文提出了一个新的约束优化问题(由于参数δ_pref通常设置为某个值, 为了简化符号, 则δ_pref将从每个函数的参数中删除)如下所示:

$ \left\{ \begin{array}{l} \mathop {\rm maximize}\limits_{\alpha ,\beta ,\gamma } \;\;\;F_1(\alpha ,\beta ,\gamma ) \;\; {\rm{or }}\;\;recall(\alpha ,\beta ,\gamma )\\ {\text{当}} \;\;precision(\alpha ,\beta ,\gamma ) \ge \delta _{precision},\alpha \ge \beta \end{array}\right. $

(5)

其中, δ_precision是一个预先定义的阈值, 并根据不同类型的推荐系统适当地调整该值. 根据不同目的对式(5)进行修改也很容易. 例如, 当recall(α,β,γ) $ \ge $ δ情况下, 最大化precision(α,β,γ), 或precision(α,β,γ) $ \ge $ δ的情况下, 最大化recall(α,β,γ), 找到最优的α、β和γ, 其中δ_recall是一个预先定义的召回率阈值. 因此, 使用IPU模型的CBCF算法, 通过用户聚类以及找到参数α、β和γ的最优值可以提高准确率、召回率和F1-score.

2.3 基于IPU模型的CBCF算法

CBCF算法通过用户聚类以及使用IPU模型分析用户间的偏好倾向从而进行推荐. 使用IPU模型的CBCF算法的核心是根据 ${\overline {C}} _c^i$ (用户簇 $Cc$ 中对项目i的偏好的均值)的结果对每个项目进行激励或惩罚. 由于评分矩阵 $R_{\rm CBCF}$ 中存在用户未评分项目, 因此无法准确计算用户向量之间的欧几里得距离(即 $R_{\rm CBCF}$ 中的行向量). 因此, 本文使用皮尔逊相关系数(PCC). PCC通过计算两个用户的共同评分之间的相关性来衡量其相似性, 两个用户u1和u2之间的相似度s(u1, u2)为:

$s(u1,u2) = \frac{{\displaystyle\sum\nolimits_{i \in I_{u1} \cap I_{u2}} {(r_{u1,i} - {\mathop r\limits^ -} _{ u1}) \cdot } (r_{u2,i} - {\mathop r\limits^ -} _{ u2})}}{{\sqrt {\displaystyle\sum\nolimits_{i \in I_{u1} \cap I_{u2}} {{{(r_{u1,i} - {\mathop r\limits^ -} _{ u1})}^2}} } \cdot \sqrt {\displaystyle\sum\nolimits_{i \in I_{u1} \cap I_{u2}} {{{(r_{u2,i} - {\mathop r\limits^ -} _{ u2})}^2}} } }}$

(6)

其中, $I_{u1}$ 和 $I_{u2}$ 分别是u1和u2评分的项目集, ${\mathop r\limits^ -} _{ u1}$ 和 ${\mathop r\limits^ -} _{ u2}$ 分别是u1, u2用户评分项目交集 $I_{u1}$ $ \cap $ $I_{u2}$ 上的评分均值. s(u1, u2)的范围是–1到1.

算法2. 使用IPU模型的CBCF算法

1. 用户簇 $\scriptstyle C \in \{ C_1, \cdots ,Cc\}$ ;

2. 初始化n, x, m的用户评分矩阵 $\scriptstyle R_{\rm CBCF}$ ;

3. $\scriptstyle{\hat{ R}}$ $ \leftarrow $ $\scriptstyle R_{\rm CBCF}$ 预测评分;

4. 初始化阈值 $\scriptstyle\alpha ,\;\beta ,\;\gamma$ ;

5. for $\scriptstyle u \leftarrow 1$ to n do

6. $\scriptstyle I_u \leftarrow $ 用户测试集中缺少评分的项目;

7. $\scriptstyle u;$

8. $\scriptstyle{\hat{ r}} _{u,Iu} \leftarrow$ 项目 $\scriptstyle I_u$ 的预测评分;

9. for $\scriptstyle i \leftarrow 1$ to $\scriptstyle|I_u|$ do

10. $\scriptstyle C_{\rm tmp} \leftarrow$ 用户u所属的用户簇;

11. $\scriptstyle{\overline{ C}} _{\rm tmp}^i \leftarrow$ 用户簇中的用户对项目i的评分均值;

12. if $\scriptstyle{\hat{ r}} _{u,i} \ge \alpha$ then

13. 将项目i推荐给用户u;

14. else if $\scriptstyle{\hat{ r}} _{u,i} \ge \beta$ && $\scriptstyle{\overline{ C}} _{\rm tmp}^i \ge \gamma$ then

15. 将项目i推荐给用户u;

16. else 项目i不被推荐;

17. end

18.end

下面着重说明算法2的整个流程: 首先, 通过聚类的结果获得聚类集合C, 并初始化n, x, m评分矩阵 $R_{\rm CBCF}$ (参见算法2中的第1、2行). 接下来, 使用基于邻域的算法预进行偏好预测, 并将预测结果保存在 ${\hat{ r}}$ 中(参阅第3行). 更具体地说, 基于用户/项目的CF算法用于评估本文提出的CBCF算法的性能. 通过求解式(5)中的优化问题, 确定阈值α、β和 $\;\gamma $ . 在for循环中, $I_u$ 是用户u的测试集中缺少评分的项, ${\hat{ r}} _{u,I_u}$ 是 $I_u$ 中的预测评分, 其中 $|I_u|$ 表示 $I_u$ 的基数. 下面通过α、β和 $\;\gamma $ 来决策是否推荐某些项目. 当 ${\hat {r}} _{u,i} \ge \alpha $ , 时, 将项目i推荐给用户u, 而不需要考虑算法1中提到的阈值 $\;\gamma $ (参考算法2中的第11、12行). 当 ${\hat {r}} _{u,i} < \alpha $ , 时, 那就需要考虑阈值 $\;\gamma $ 以及 ${\overline{ C}} _{\rm tmp}^i$ , 其中 ${\overline{ C}} _{\rm tmp}^i$ 表示某项用户簇的偏好均值. 当 ${\overline{ C}} _{\rm tmp}^i < \gamma $ 时, 即使 $\beta \le {\hat {r}} _{u,i} < \alpha $ , 项目i也不会被推荐. 这因为当 ${\overline{ C}} _{\rm tmp}^i < \gamma $ 时, 给对项目i进行惩罚. 当 ${\hat {r}} _{u,i} > \beta $ 和 ${\overline{ C}} _{\rm tmp}^i \ge \gamma $ 时, 将向用户u推荐项目i (参考第13、14行). 当 ${\hat {r}} _{u,i} < \beta $ (参考第15行)时, 项目i不会被推荐.

求解式(5)中的优化问题, 确定阈值α、β和γ. 在迭代执行算法2的同时不断改变α、β和γ值. 也就是说, 根据式(5), 迭代执行算法2中的第4~17行, 来获取α、β和γ的最优值.

使用IPU模型的CBCF算法总结如下:

(1)通过使用IPU模型以及CBCF算法来决策是否将项目i推荐给活跃用户u.

(2)当(即 ${\hat{ r}} _{u,i} \ge \alpha$ ), 那么将项目i推荐给用户u.

(3)当 ${\hat{ r}} _{u,i} \ge \beta$ 和 ${\overline{ C}} _c^i \ge \gamma$ , 向用户u推荐项目i, ${\overline{ C}} _c^i$ 是用户簇 $C_c$ 对项目i的偏好均值.

3 实验 3.1 实验数据集

本节描述数据集以及数据结构. CBCF常用于非冷启动用户, 但它对冷启动用户同样有效. 本文使用MovieLens数据集下的载地址为: https://grouplens.org/datasets/movielens/, 其中有好几种版本, 对应不同数据量, 本文所用的数据为100 KB的数据集.

100 KB的数据集具有以下属性:

(1)评分最高为5星;

(2)每个用户至少有20条评分记录;

(3) 100 KB数据集有100 000条评分记录;

(4) 100 KB数据集有943个用户和1682部电影.

值得注意的是, 从movieens 100 KB数据集获得的评分矩阵的稀疏度(即评分矩阵中丢失的单元格数与单元格总数的比值)为93.7%. 数据稀疏性问题的一个普遍解决方法是采用数据填补的方式, 对缺失的单元格用零补全^[18].

即使采用数据填补的方法能显著提高预测精度, 本文的重点在给定准确率的条件下最大化召回率(或F1- score)而非解决数据稀疏性问题, 因此没有采用数据填补方法. 数据结构描述如下.

假设推荐系统中有一组用户U和一组项目I, 如下:

$\left\{\begin{array}{l} U\mathop = \limits^{\Delta} \{ u_1,u_2,\cdots,u_n\} \\ I\mathop = \limits^{\Delta} \{ i_1,i_2,\cdots,i_m\} \\ \end{array} \right.$

(7)

其中, n和m分别表示用户数和项目数. 评分矩阵 $R_{\rm CBCF}$ 如下:

$R_{\rm CBCF} = \left( {\begin{array}{*{20}{c}} {r_{1,1}}&{r_{1,2}}&{r_{1,3}}& \cdots &{r_{1,m}} \\ {r_{2,1}}&{r_{2,2}}&{r_{2,3}}& \cdots &{r_{2,m}} \\ {r_{3,1}}&{r_{3,2}}&{r_{3,3}}& \cdots &{r_{3,m}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {r_{n,1}}&{r_{n,2}}&{r_{n,3}}& \cdots &{r_{n,m}} \end{array}} \right)$

(8)

其中, $r_{u,i}$ 是用户u对项目i的评分, 其中 $u \in \{ 1, \cdots ,n\} $ $i \in \{ 1, \cdots ,m\} $ . 值得注意的是, $R_{\rm CBCF}$ 可以是用户的显式评分, 也可以是用户的隐式评分. 如果用户u未对项目i进行评分, 那么 $r_{u,i}$ 为空.

将用户集U分为多个用户簇, 用户簇是评分矩阵 $R_{\rm CBCF}$ 中的一组类似的用户. 为了聚类U, 定义了n个用户向量, 每个用户向量由m个元素组成.

$U_b = [r_{b,1},r_{b,2}, \cdots, r_{b,m}]$

(9)

对于 $b \in \{ 1, \cdots ,n\} $ . 假设n个用户向量聚集到C个用户簇中, 其中的用户簇集合C表示为:

$C = \{ C_1,C_2, \cdots ,C_c\} $

(10)

同一个用户簇中用户的偏好相似度比不在同一个用户簇中的其他用户更接近. 例如, 假设有4个用户向量, 分别为u1=[2, 0, 1, 0], u2=[0, 4, 0, 2], u3=[3, 0, 2, 0]和u4=[0, 3, 0, 2]. 需要将这4个向量分成2个簇. 那么,u1和u3将被分到一个族中, 根据用户的评分, 他们是相似用户, 因为(u1, u3)之间的欧几里得距离比(u1, u2)、(u1, u4)、(u3, u2)和(u3, u4)等其他组合的欧几里得距离更近.

数据结构如表2所示. 数据由以下3个字段组成: 用户ID、项目ID和用户评分. 例如, 如果用户u1对项目i1的评分为4.0, 那么插入一个新的记录“ ${{{u}}1}|{i1}|4.0$ ”.

3.2 实验结果与分析

本文从准确率、召回率和F1-score方面来评估使用IPU模型CBCF算法的性能. 本实验中, 除特殊说明外, 默认采用基于项目的CF, 因为它在基于邻域CF推荐的准确率上有更好的性能, 这将在本节后面进行验证. 本文使用Apache Mahout来构建执行机器学习任务(如CF、聚类和分类)的环境. 当满足以下条件时, 假设推荐结果为真:

(1)实际评分为4.0或5.0的项目向用户推荐.

(2)实际评分低于4.0的项目不向用户进行推荐.

本实验中, 谱聚类和FCM聚类算法均设置c=10; 根据文献[19]将FCM聚类的模糊度m设置为2; 并将FCM聚类的收敛阈值设置为 ${10^{ - 4}}$ . 在FCM聚类中, 将对象分配给具有最高系数的聚类. 本实验中, 除特殊说明外, 默认采用谱聚类. 图2比较了簇间和簇内的欧几里德距离, 以证明聚类的效果. PCC的值在–1.0和1.0之间, 其中1.0和–1.0意味着两个对象(如用户)分别具有最高的正相关和负相关. 由于大多数聚类算法不采用负相关, 因此两个用户u1和u2之间的PCC值, 即s(u1,u2), 如下所示:

$\left\{ \begin{array}{l} s(u_1,u_2) \leftarrow 1 - s(u_1,u_2)\; {\rm{for}} \;s(u_1,u_2) \in [0,1]\\ s(u_1,u_2) \leftarrow - (s(u_1,u_2) - 1)\;{\rm{for }}\;s(u_1,u_2) \in [ - 1,0] \end{array}\right. $

(11)

接近0表示高度正相关, 而接近2表示高度负相关. 如图2所示, 从簇0的角度看, 簇内距离小于簇间距离. 因此, 基于PCC的聚类是有效的.

图3显示了当阈值γ设置为3.4, α和β(分别对应于给予惩罚和激励的阈值)对F1分数的影响. 当α=3.7和β=2.9时, 使用IPU模型的CBCF算法的F1的最大值为0.7451. 实验结果表明, 随着α和β的增加, F1-score 降低, 因为随着α和β的增加, 召回率的下降幅度大于准确率的上升幅度. 如果α和β都很大, 那么准确率和召回率分别增加和减少. 然而, 由于召回率的下降幅度大于准确率的上升幅度, F1-score 也相应降低. 例如, 在图3中, 当α=3.7, β=2.9, γ=3.4时, 准确率为0.6595, 召回率为0.8564; 当α=4.4,β=4.4,γ=3.4时, 准确率为0.6853, 召回率为0.076.

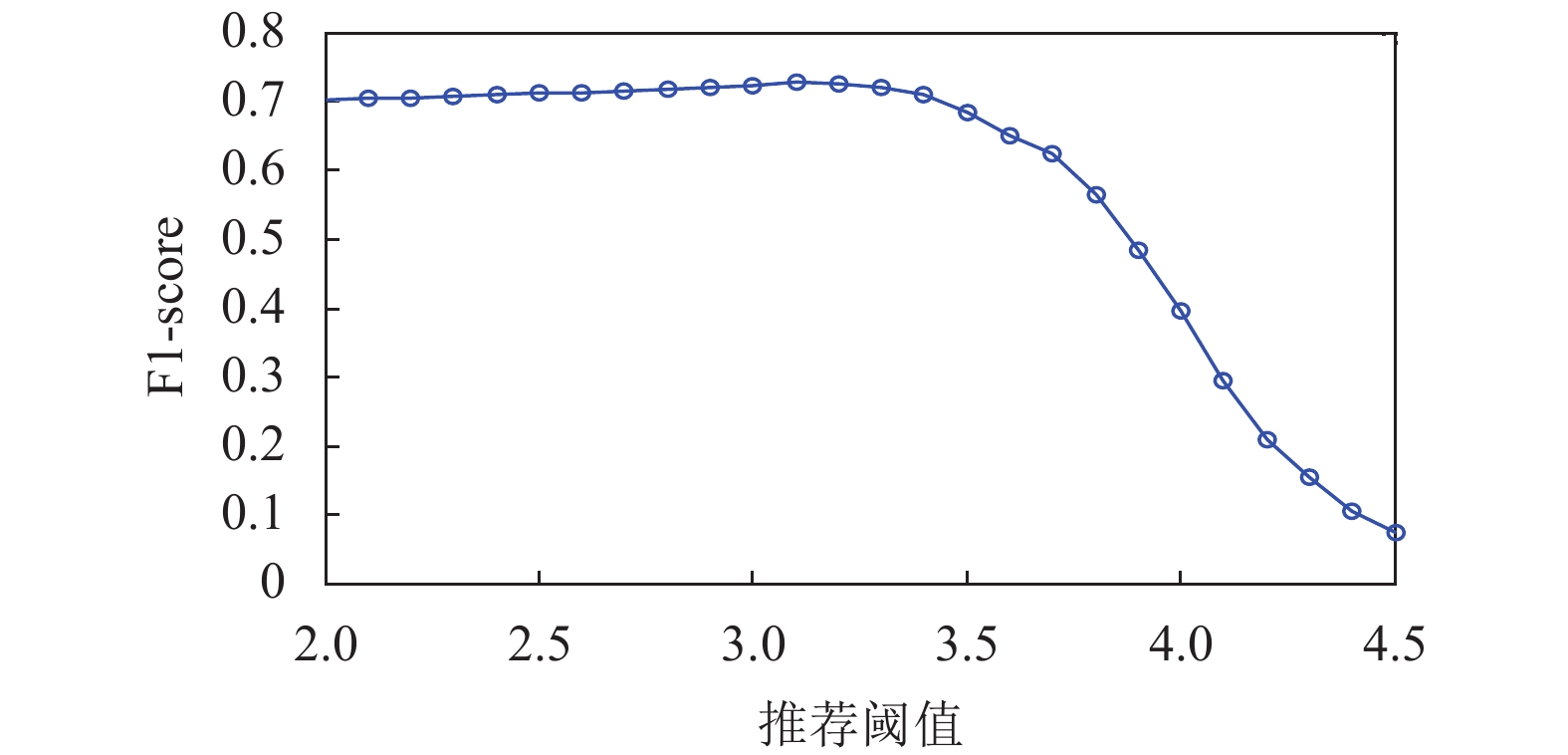
图4显示当采用不考虑聚类(即γ=0)的基于项目CF算法时, F1-score随着推荐阈值的变化趋势, 如果某个项目的预测评分大于推荐阈值, 那么将向用户推荐相应的项目. 如果实际评分超过4.0, 那么该推荐是有效的. 如图4所示, 当阈值为3.1时, F1-score的最大值为0.7282. 实验结果表明, 总体趋势与图3相似, 与不采用聚类的基于项目的CF的算法相比, 本文所提出算法的 F1-score 提高近3%.

表3显示了使用IPU模型CBCF算法和不使用聚类的基于项目的CF算法在给定准确率情况的召回率和F1-score. 基于项目的CF算法(未使用聚类算法)中, 当阈值设置为4.0, 准确率为0.7449时, 召回率的最大值为0.2815. 使用IPU模型CBCF算法中, 当准确率为0.7449, α=3.9, β=2.1, γ=4.2时, 召回的最大值为0.4343. 召回率提高近50%. 也就是说, 如表3所示, 在准确率相同的情况下, 与基于项目的CF(未使用聚类算法)相比, 本文提出的算法具有非常高的召回率. 从图3、图4和表3可见, 本文提出的算法在给定准确率的情况下, 召回率或F1-score得到了很大的改进.

一般来说, 推荐阈值越小, 准确率越低, 召回率越高, 反之亦然. 然而, 如前所述, 当阈值变得非常大时, F1-score会迅速下降, 因为召回率的下降幅度大于准确率的上升幅度.

本文提出的CBCF算法中, 也可以使用基于用户的CF代替基于项目的CF通过求解式(5), 找到参数α, β和γ最优值, 对使用IPU模型基于项目的CF算法分别使用谱聚类和FCM聚类算法的性能进行比较, 如表4所示, 以及对采用IPU模型基于用户的CF算法分别使用谱聚类和FCM聚类算法的性能进行比较, 如表5所示, 以上测试数据都不包含冷启动用户. 根据实验结果, 总结如下: 1)基于项目的CF算法比基于用户的CF在F1分数上有更好的表现; 2)基于FCM聚类的算法比谱聚类有更好的表现.

此外, 还比较了本文提出的算法(采用谱聚类)与未使用聚类的CF算法基于冷启动用户(评分项目数少于20)数据的性能. 由于movieens 100 KB数据集不包含冷启动用户的记录, 根据文献[20]修改了实验设置. 具体来说, 本文选取了有过20~30部电影评分记录的290名用户的数据作为测试集, 并随机抽取每个用户3~20个评分项目. 原始数据集中剩余的653个用户作为训练集. 表6中的结果与非冷启动用户的结果具有相似的趋势, CBCF算法的性能优于未采用聚类的CF算法.

4 结束语

通过对推荐系统的不断探索, 本文提出了使用IPU模型的CBCF算法, 并提出了一个约束优化问题, 即在给定准确率的条件下最大化召回率(或F1-score). 为此, 应用聚类算法, 根据实际评分和皮尔逊相关系数将用户分为多个聚类, 并根据同一个聚类内用户的偏好倾向, 对每个项目进行激励或惩罚. 实验结果表明, 采用IPU模型的CBCF算法在给定准确率的条件下, 召回率或F1-score有显著地提高. 本文未来研究的一个方向是通过利用基于模型的CF算法(如矩阵分解)的特性, 设计一种新的基于聚类的CF算法.