2. 中国石油大学(华东) 海洋与空间信息学院, 青岛 266580
2. College of Oceanography and Space Informatics, China University of Petroleum, Qingdao 266580, China
人体跌倒指的是由于身体机能失调, 平衡能力不足等原因引起的事故, 随着社会的发展, 人口老龄化也呈现上升的的趋势, 由于跌倒引起的老人受伤甚至是死亡事故日渐增长, 预防和救治跌倒的老人已经成为社会上愈发关注的焦点, 为了减轻老人因跌倒而产生的伤害, 跌倒检系统也日渐完善, 但我们所了解到的大部分的检测系统分为基于环境感知类的跌倒检测和基于三维传感器的跌到检测法; 环境感知类中视频图像检测方法由于存在成本高、区域局限性、隐私问题, 不能高效精准的对跌倒的老人进行报警; 三维传感器又分为穿戴式设备检测、地面传感器、压力传感器和内置加速度传感器、陀螺仪等检测方法、但由于传感器佩戴位置的不同、阈值处理灵敏度、跌倒产生的压力不同外界因素的影响会导致检测结果不精确. 所以为了老人在跌倒的时候更精准的检测并预警, 使老人因跌倒而造成的伤害甚至是死亡的风险降到最低, 所以关于跌倒检测的研究是有重要意义的.
针对目前跌倒研究准确性低、误报率高等缺陷, 本文提出一种基于人体模型的空间三维坐标关节点的跌倒检测方法, 该方法首先是通过构建父子节点关联的人体模型结构, 然后对人体关节点的空间三维坐标进行位置预测, 并将子节点的空间三维预测位置聚合到父关节点以达到对跌倒行为的精准检测, 最后通过实验证明了该方法的准确性与可行性.
2 相关研究目前已有得研究成果中, 针对老人跌倒检测主要有两类技术:
(1)基于环境感知类的跌倒检测[1-3], 该种技术主要是通过日常生活中的视频检测系统, 监视老人的的日常行为活动, 并利用决策树、朴素贝叶斯、K均值聚类等监督分类模型算法对其行动特征进行跌倒分析, 该种方法虽然可以达到很高的准确率, 但由于制作的成本过高, 检测的范围存在局限性, 隐私容易发生泄漏等问题.
(2)基于三维传感数据的跌倒检测: 该种技术又可以分为加速度阈值处理法[4.5]、压力传感器、地面传感器等穿戴式内置传感器检测设备[6-13], 加速度阈值法由于对数据的计算量很小, 所以长时间的检测过程中会产生误报的问题, 相比阈值法利用机器学习模型对压力传感器获取的数据进行跌倒分析在灵敏度、准确性、高效性等方面有显著提高, 但是人工神经网络等机器学习模型对跌倒分析的时候受到行为特征、分类算法等因素的影响、在对一些常见的运动进行分析时候会产生很大的错误率.
3 基于三维坐标的人体行为建模 3.1 人体行为模型的构建在对人体模型扫描重构的过程中, 由于人体关节自由度相对较多, 结构复杂, 为了对关节点进行高效预测所以在人体建模的过程中首先以脊柱中的胝椎关节作为人体骨骼模型的父节点, 而后按照人体模型的结构向四肢延伸, 形成一种父子节点关联的骨骼结构, 从而架构出基本的人体模型.
人体关节模型搭建完成之后, 每个人体关节点都会处于当前的三维坐标系之中, 所以在对行为运动分析时, 要充分考虑父子关节点所处空间的三维坐标位置变化, 并且需要考虑到在运动过程中经常性做出例如手臂环绕等重复性的动作的时候, 手臂当前子关节的空间位置会发生变化, 但是父关节所处的身体中心的全局坐标未发生变化, 因此需要建立以父关节为原点全局坐标系, 各个子关节点为局部坐标系的关节三维空间坐标轴. 只有父子关节点所处的三维位置空间同时发生变化的时候才会判定为跌倒状态.
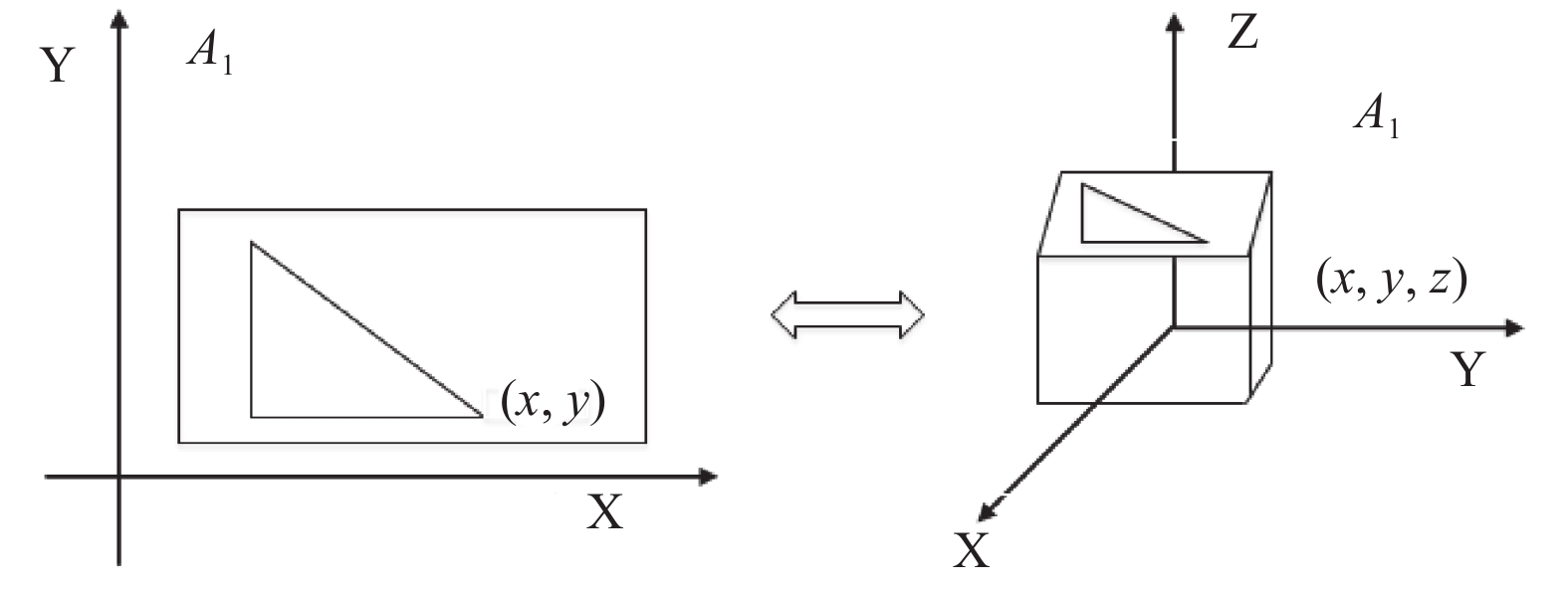
3.2 三维关节坐标的映射因为大部分实验中的人体行为关节数据获取的只有二维平面坐标, 这就导致了在实际运动过程中会产生关节点位置预测结果不精确等局限性, 然而人体在运动过程中各个肢体节点节点所处于的是空间三维平面, 所以为了解决这一问题, 我们需要对相应的关节点二维平面坐标进行映射处理, 将肢体节点的二维平面坐标
|
图 1 坐标转换 |
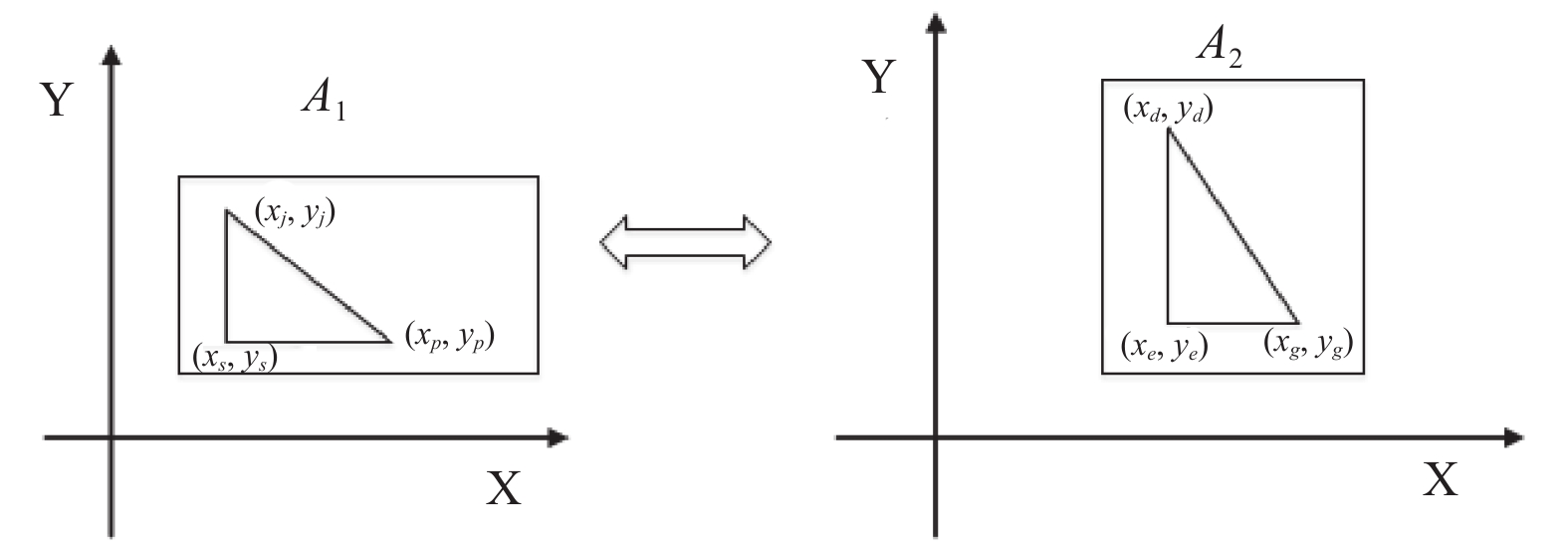
为了实现二维到三维的映射关系, 我们需要在二维平面上任取3个点
但是需要注意的是此时点所处的坐标系是不同的. 如图2所示.
|
图 2 坐标旋转 |
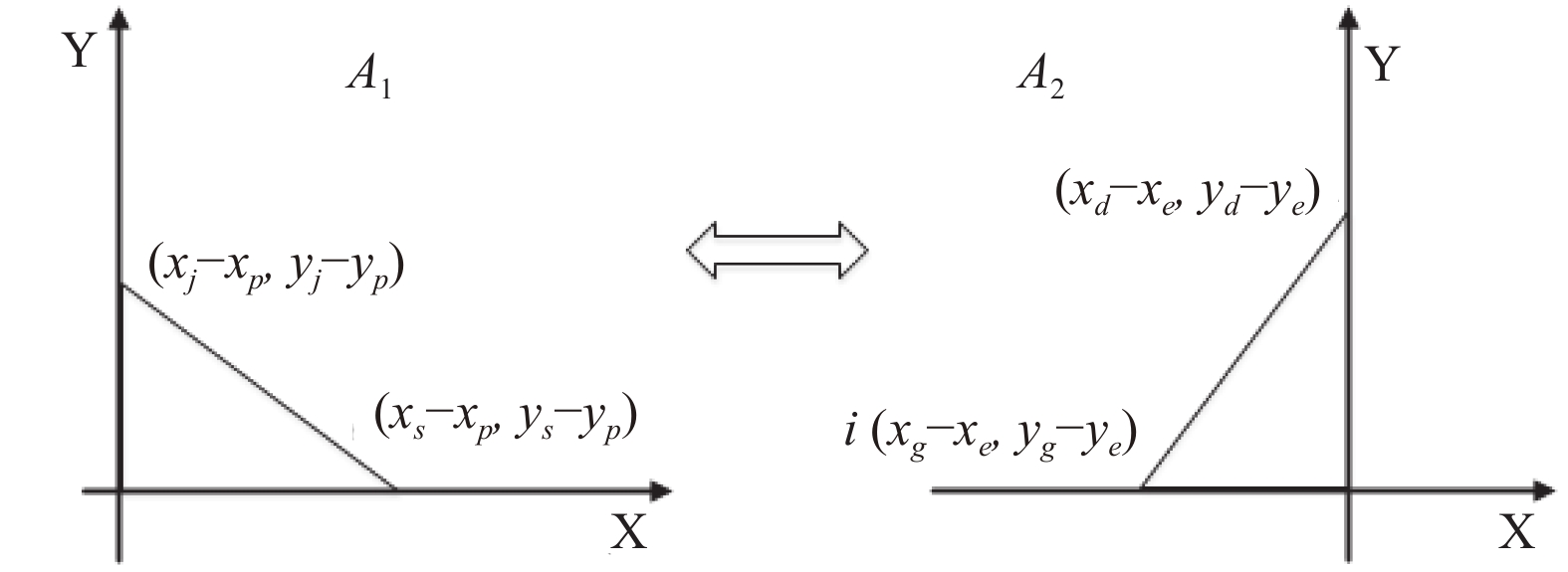
我们可以将人体模型的父子关节点所处的一个坐标平面转换为三维空间坐标轴中的一个横切的平面, 也就是说关节点所处的平面与三维空间的横切面是平行的, 经过坐标变换后可以看出两个不同的平面Z轴的高度相同, 这样用函数表示就变成了
|
图 3 坐标平移 |
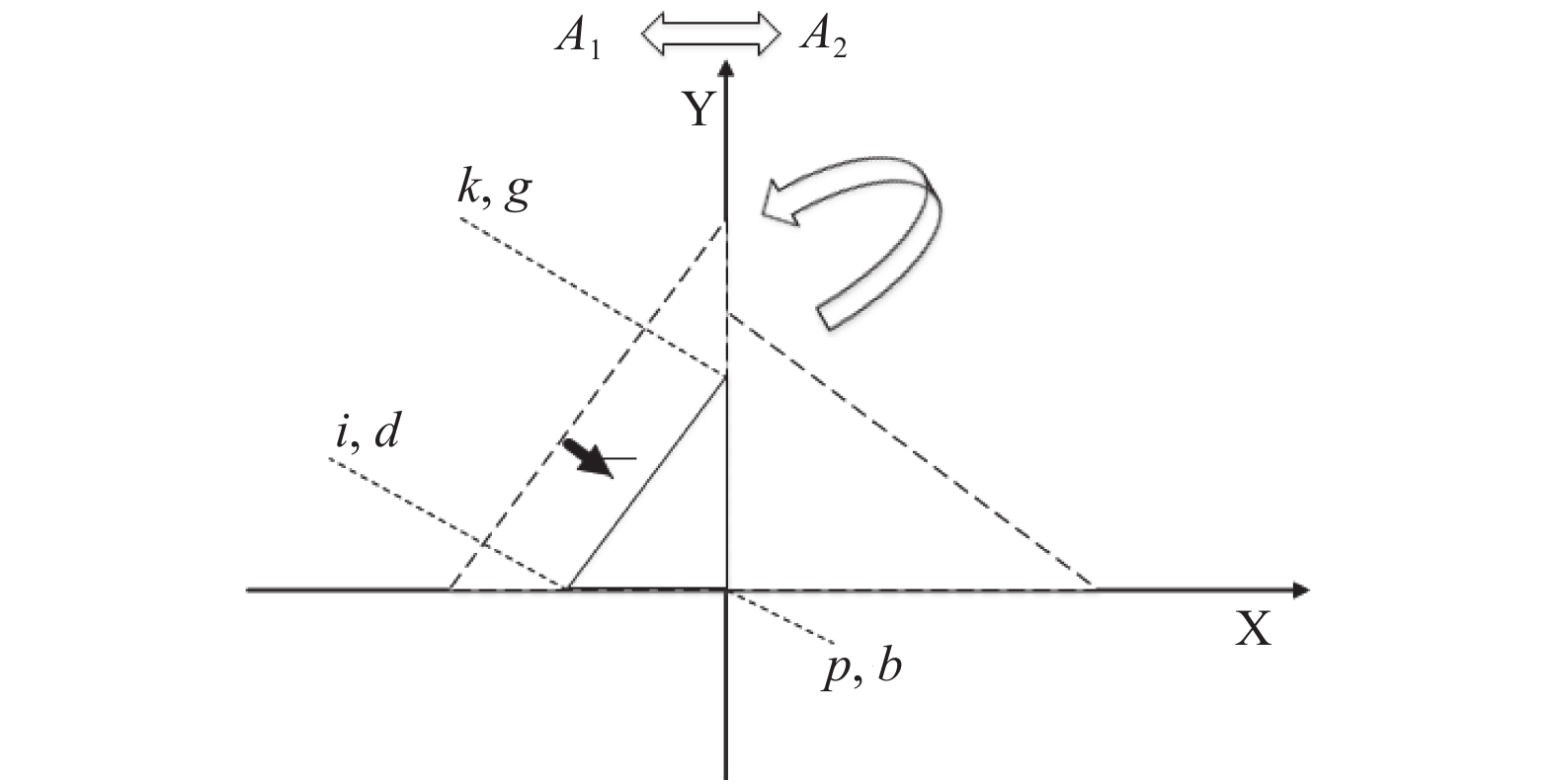
将两个平面的坐标经过旋转, 使得A1面和A2面的其中一点重合, 然后围绕原点进行旋转、缩放操作, 使A1和A2重合, 如图4.
|
图 4 旋转缩放图 |
为了求出映射后的三维坐标, 我们需要对经过旋转、缩放后的两
| $\left\{ \begin{split} &{A_1}{{ = }}\left(\begin{array}{*{20}{c}} {{{{x}}_{{j}}}{{ - }}{{{x}}_p}}&\!\!{{{{x}}_s}{\rm{ - }}{{{x}}_p}}\\ {{y_j}{{ - }}{y_p}}&\!\!{{y_s}{{ - }}{y_p}} \end{array}\right)\\ &{A_2}{{ = }}\left(\begin{array}{*{20}{c}} {{{{x}}_{{d}}}{\rm{ - }}{{{x}}_e}}&\!\!{{{{x}}_g}{{ - }}{{{x}}_e}}\\ {{y_d}{\rm{ - }}{y_e}}&\!\!{{y_g}{{ - }}{y_e}} \end{array}\right)\\ &{{T = }}\left(\begin{array}{*{20}{c}} {{a}}&\!\!{{b}}\\ c&\!\!d \end{array}\right) \end{split}\right.$ | (1) |
其次, 在
通过逆矩阵变换求解
| $\left[ {\begin{array}{*{20}{c}} {{a}}&b \\ c&d \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_m} - {x_e}} \\ {{y_m} - {y_e}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_n} - {x_f}} \\ {{y_n} - {y_f}} \end{array}} \right]$ | (2) |
根据上面公式可以推导式(3)如下:
| $\left\{ \begin{array}{l} {{{x}}_n}{{ = a}}{{\rm{x}}_m} - a{x_e} + b{y_m} - b{y_e} + {x_f}\\ {{{y}}_n}{{ = c}}{{\rm{x}}_m} - c{x_e} + d{y_m} - d{y_e} + {y_f} \end{array} \right.$ | (3) |
所以输入
在得到三维坐标后, 我们需要对关节点所对应的三维坐标进行目标概率位置预测, 首先根据人体的关节自由度, 按照父子关节点层级结构, 通过父节点与子节点之间的关联性沿四肢延伸到整个系统模型, 并由此构建出一种骨骼关节树的结构, 我们可以从人体模型的末端开始计算, 最底层的自关节点相对应的父节点的数量关系我们可以看做一个等比关系. 这样我们可以计算父关节与子关节点数列之和公式如下:
| $ {a_{{n}}} = \frac{{{a_1} \cdot {q^{{n}}}}}{q},\;{\text{求出}}{{{s}}_n} = \frac{{({a_1} - {a_{{n}}}{q^{}})}}{{1 - q}} $ | (4) |
当其中一个关节处于人体模型的X层的L个节点的时候, 则可以得出该节点的位置位为
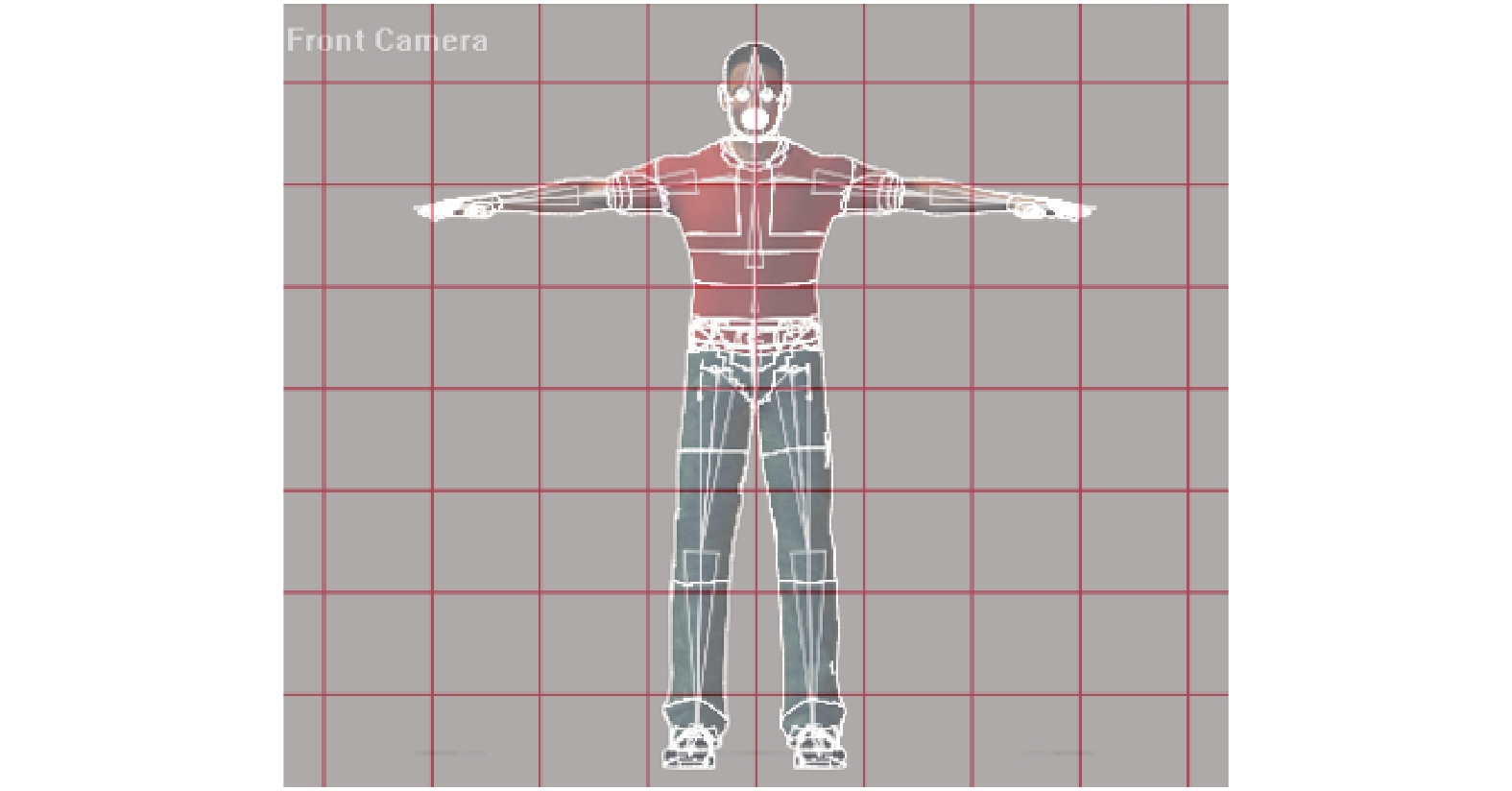
|
图 5 关节点位置模型 |
图5中我们可以看出不同的子关节点落在不同的单元格内, 通过单元格来预测模型中父子关节点位置的变化, 首先为了确保人体行为运动过程中的父子关节点落于单元格中以及对关节点运动过程中的位置预测变化值, 我们需要设置两个变量作为衡量关节点与单元格之间位置的变化性以确保对运动过程中关节点实时所处的空间位置进行精准预测, 因此我们设置一个置信度P和关节点node, 当所要检测的关节点node的位置落于单元格中那么相应的置信度P就会变成1, 如果关节点node脱离相对应的单元格, 那么置信度设置为0, 当人体处于运动过程中, 关节点node在单元格空间内的位置变化会趋于平稳, 当发生跌倒时候, 关节点在单元格内的位置会因为跌倒而产生剧烈变化, 这时候我们对跌倒进行检测需要考虑到两方面: 一方面是关节点node已经脱离位置预测单元格, 另一方面是关节点node仍位于单元格内, 我们需要对两种情况分别对跌倒行为进行检测, 所以我们关节点node的单元格空间位置预测算法要分为两部分. 但是通过具体实验发现关节点node在单元格预测处理过程中会因为数据的跨度太大导致预测结果不准确, 所以我们需要再设置两个优化参数
包含目标关节点时候:
| $ \sum\limits_{{{i}} = 0}^{{N^2}} {\sum\limits_{j = 0}^B {\mathop I\nolimits_{ij}^{node} } } {({P_i} - {{\hat P} _i})^2} $ | (5) |
不包含目标关节点时候
| ${\lambda _{{{\rm null}}}}\sum_{{{i}} = 0}^{{N^2}} {\sum_{j = 0}^B { I_{ij}^{\rm null} } } {({P_i} - {{\hat P} _i})^2}$ |
实验过程中除了存在置信度位置损失值之外, 当关节点落于的初始单元格边框界的边框大小也会对结果产生影响, 这是因为在实验中如果关节点落于较小的单元格边界框上的时候, 那么相对应的关节点的位置预测会更加频发的发生, 导致子关节点的预测效果变化特性大, 所以为了解决这个问题, 我们将初始单元格的宽高两个值变为为
| $ {\lambda _{{p}}}\sum_{{{i}} = 0}^{{N^2}} {\sum_{j = 0}^B {\mathop I\nolimits_{ij}^{node} } } \left[ {{{(\sqrt w - \sqrt {{\hat {w}} } )}^2} + {{(\sqrt h - \sqrt {{\hat h} } )}^2}} \right] $ | (6) |
而后将映射后的三维坐标代入到行为预测算法模型中, 通过构建的父子关节点运动模型的坐标位置预测值来对人体跌倒的行为进行检测, 公式如下:
| $\begin{split} {x_2}{\lambda _p}\sum_{i = 0}^{N^2} {\sum_{j = 0}^B {I_{ij}^{node}} \left[ {{{\left( {x_n - {{\hat x }_n}} \right)}^2} - {{\left( {y_n - {{\hat y }_n}} \right)}^2}} \right]} = &{\lambda _p}\sum_{i = 0}^{{N^2}} {\sum_{j = 0}^B {I_{ij}^{node}} } \left\{ {\left[ \left( {a{x_m} - a{x_e} + b{y_m} - b{y_e} + {x_f}} \right) - \left( {a{x_m} - a{x_e} + {{\hat {by} }_m} - b{y_e} + {x_f}} \right) \right]^2} \right.\\ &\left.+ {\left[ \left( {c{x_m} - c{x_e} + d{y_m} - d{y_e} + {y_f}} \right) - \left( {c{x_m} - c{x_e} + {{\hat {dy} }_m} - d{y_e} + {y_f}} \right) \right]^2} + {\left( {{\textit{z}_n} - {{\hat {\textit{z}} }_n}} \right)^2} \right\} \end{split} $ | (7) |
当利用父子关节点三维算法模型完成之后, 将跌倒检测算法导入到人体模型中, 并模拟人体在空间三维坐标轴中进行相应的运动. 模型在跌倒或者异常行为发生并在一段时间内未恢复站立状态时, 相应的关节点node所处单元格数据检测会发生急剧误差值转换, 这里的误差值变化指的是, 同一落于单元格内的关节点在正常行为与发生跌倒行为的时候关节点相对于单元格内的预测位置的差值以及关节点的两种状态的损失置信度差值, 当处于正常运动过程中我们可以发现误差值的前后转换状态会呈现出一种平稳的状态, 但是当人体发生跌倒状态之后, 可以发现各个关节点的置信度损失值脱离原本的运动曲线, 此时关节点的脱离原本正常运动过程中的单元格, 而后通过关节点的单元格位置预测算法的差值可以分析出跌倒前后关节点的三维空间映射坐标, 对应检测的位置也发生剧烈变化, 所以通过分析落于单元格内的关节点的误差变化来判断人体是否处于跌倒状态. 行走模型图如图6所示.
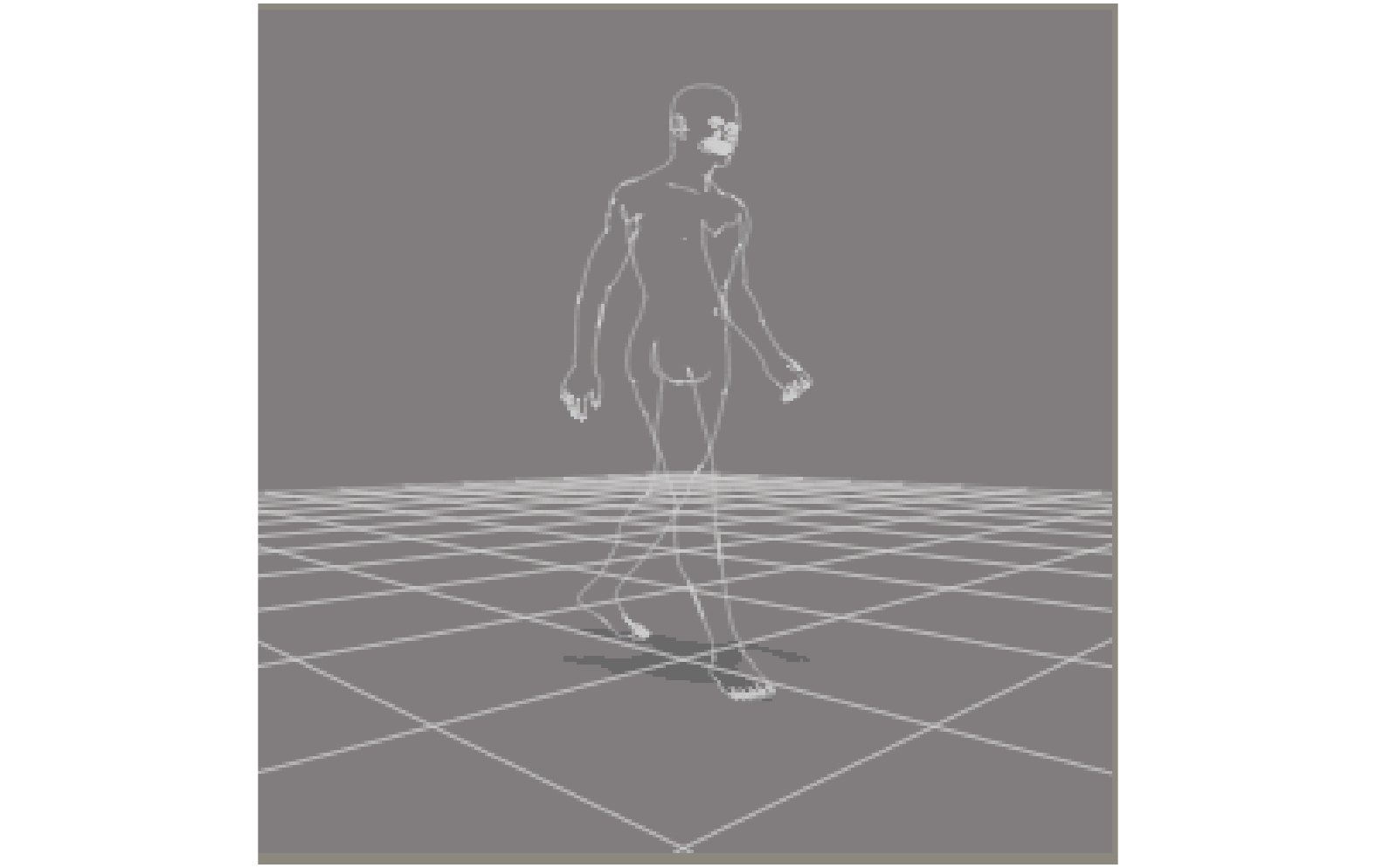
|
图 6 跌倒检测模型图 |
4 跌倒检测算法实现 4.1 跌倒检测算法概述
跌倒关节点的位置预测值与通过父子链接关系得关节点模型结构可很好地检测出当前所处的行为状态, 本文通过人体仿真模型模拟人体一系列的运动, 使老人的行为运动可以更清楚的呈现出来, 便于实验的观察与研究, 在实验结果中显示出来的人体下蹲, 战立, 以及跌倒的行为运动都与真实运动情况像符合. 所以为了进更精准的跌倒检测的研究, 通过可穿戴设备中的内置的RLS位置传感器, 获取身体佩戴位置关节点的位置信息, 而后映射为三维空间坐标, 然后通过父子关联结构进行位置误差值预测, 本文提出的跌倒检测算法流程图如图7所示.
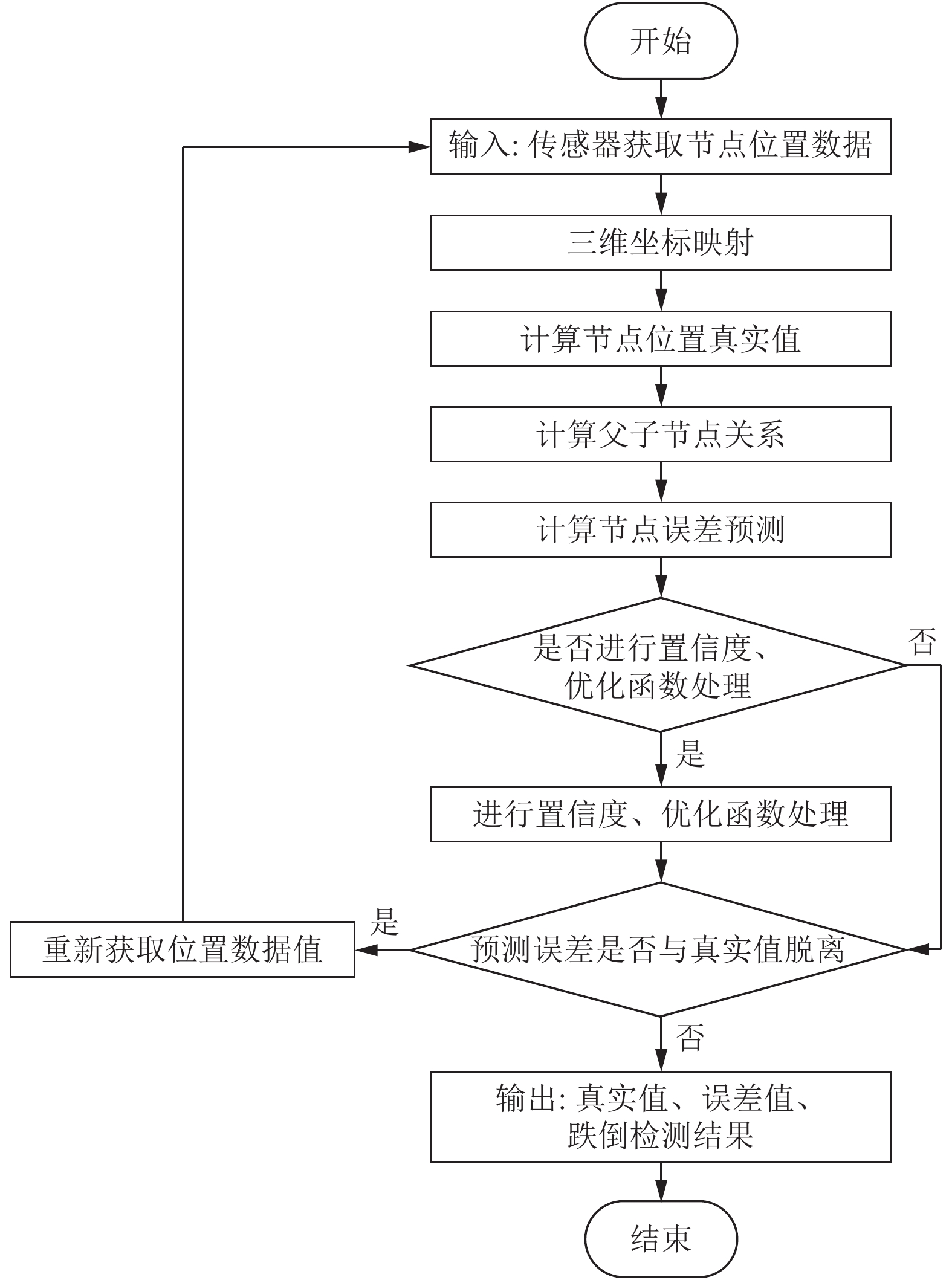
|
图 7 系统流程图 |
4.2 跌倒检测算法详述
输入: 穿戴式传感器获取的当前关节点的位置数据.
1) 通过穿戴式设备中的内置的RLS高性能微型磁编码关节位置传感器获取当前关节点的位置信息数据, 计算出当前实时关节点的位置误差值.
2) 依次对取出当前关节点运动位置的坐标数据值进行空间三维坐标映射并输入到位置误差公式中进行误差值的计算.
输出: 父子关节点所处的空间三维坐标误差值与真实值以及是否跌倒结果3个数值.
1) 输出相应关节点映射出后的三维坐标位置的误差值, 而后进行位置误差值与真实值的对比数据
2) 比较输出的两个值, 如果位置误差值远离当前关节点位置真实值的运动范围, 则证明人体已完全脱离正常行为运动状态, 处于跌倒状态.
算法过程详述:
1) 根据父子关节点相互关联性这一特点构建出人体运动学模型, 并根据关节所处的左右子节点的位置关系推导出父类关节点的位置信息, 详见本文第3.2节.
2) 将关节点所处的平面二维坐标经过坐标平移, 置换, 翻转以及矩阵变化等方法映射出二维平面关节点所处的三维空间坐标. 利用推导出对应节点所处的三维空间坐标节点位置. 详见本文3.1节.
3) 根据人体运动模型的关节自由度将人体所处的空间划分为N×N的空间单元格, 而后根据落入单元格内的关节点位置的置信度, 预测误差值等数据对关节点的实验数据值与原始行为位置值进行预测估计, 判断当前节点是否处于异常行为状态, 详见本文3.3节.
4) 子节点的异常行为位置预测值计算后, 根据父子节点的链接关系, 推导出父节点的置信度与空间位置误差值并与当前父节点所处的单元格位置误差值进行数据比较分析, 若父子节点同时处于跌倒行为则证明人体处于跌倒状态.
5 系统实验及分析实验中多次模拟人体从站立行为变为下蹲运动以及跌倒最后恢复到站立这几个阶段的实验关节点误差值数据, 图中横坐标表示时间, 纵坐标表示关节点的位置误差值, 从图8我们可以看出, 在跌倒状态发生时候, 随着时间的递增所有落于单元格中的关节点预测位置相应的误差值数据会变化, 从图中横坐标0–5这一段时间可以看出, 人体做重复的上下蹲动作, 所以关节点的误差值会上下波动, 然后5–10这一段时间表示在跌倒发生之后, 人体由于刚产生跌倒行为, 人会挣扎起身, 这个时候关节点的误差值会小幅度波动, 如果随着时间增加关节误差值的变化如10–20这一段波形, 那么证明人体已经处于完全跌倒状态, 最后经过一段时间, 人体慢慢从跌倒恢复到站立的行为.
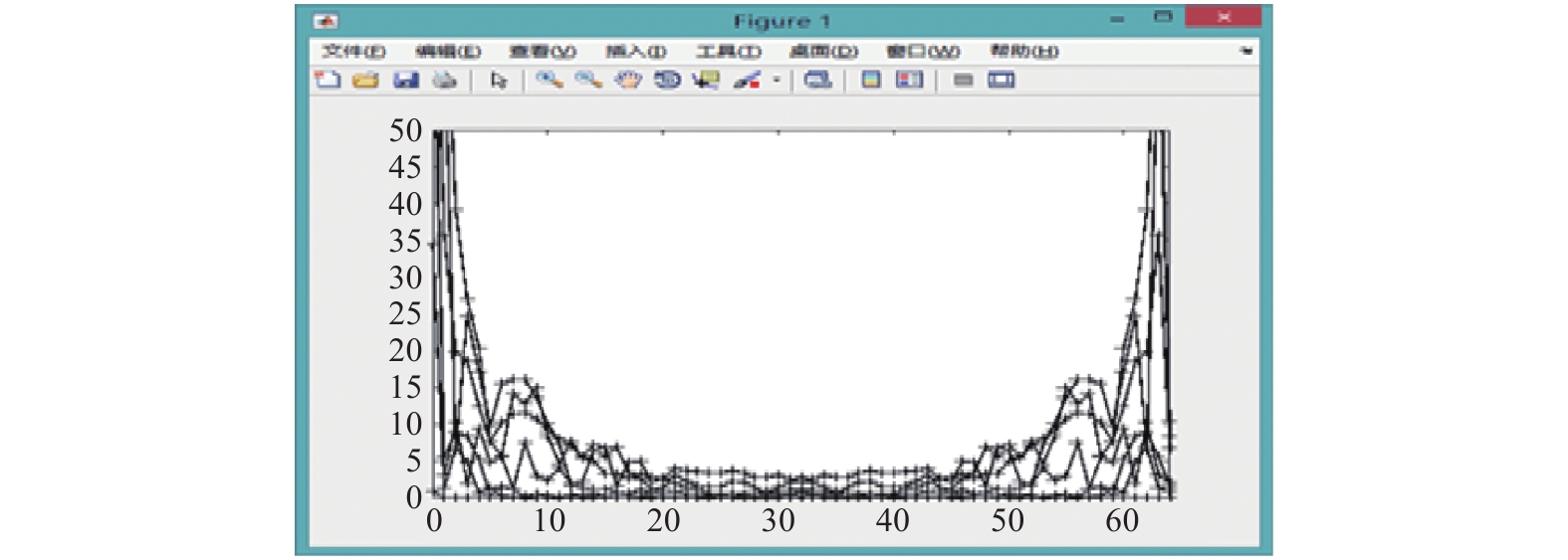
|
图 8 关节误差波动图 |
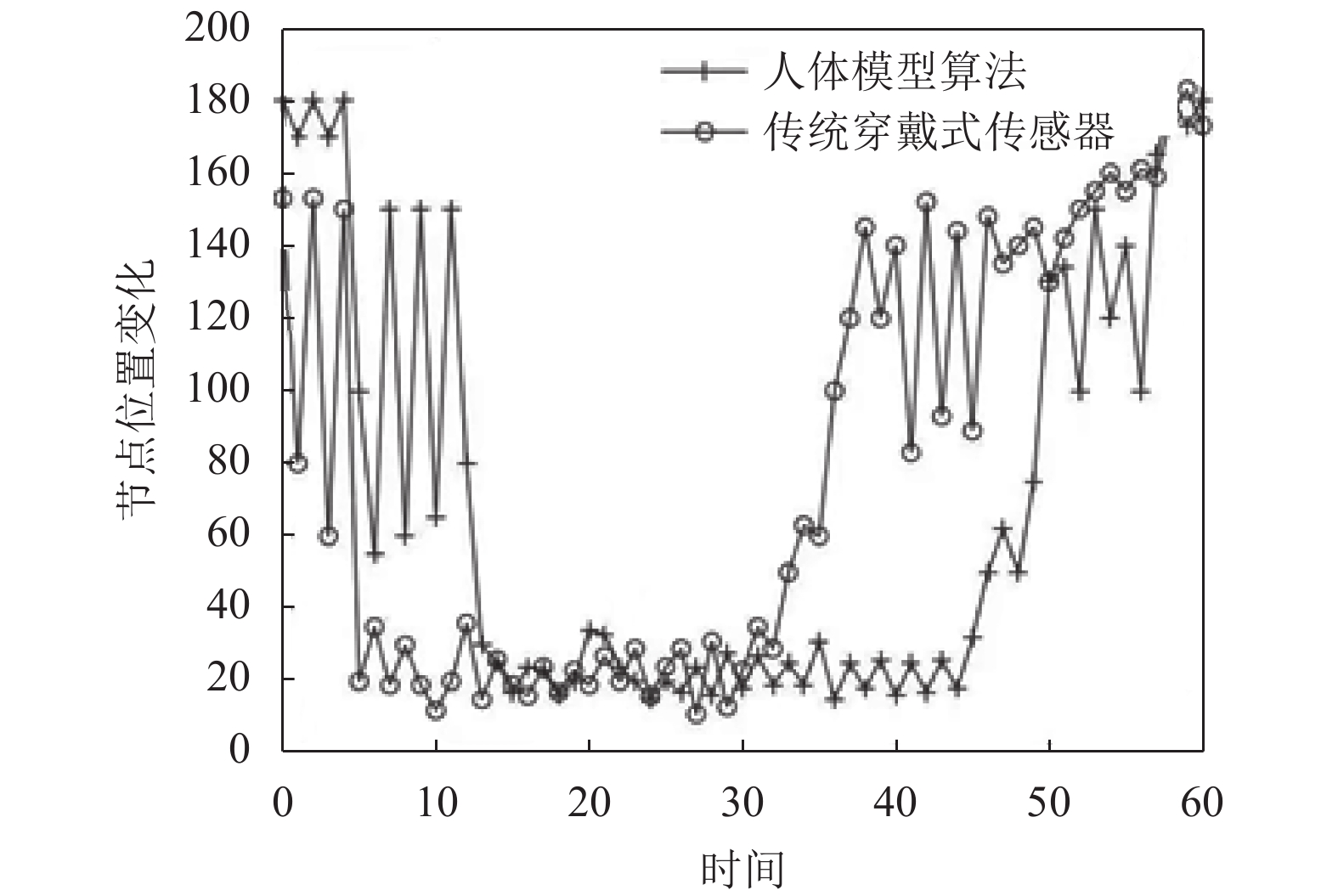
在进行跌倒行为检测的的时候, 我们同时获取人体模型运动行为过程中关节点的空间位置数据, 然后在Matlab环境中对关节点数据进行分析, 如图9.
|
图 9 节点空间位置变化曲线图 |
从图9中我们可以看出, 在本实验过程中, 关节点位置由于站立状态, 空间位置变化平稳, 当下蹲运动发生时候, 可以看出关节点的空间位置剧烈波动, 当发生跌倒行为时候, 先是在所处空间位置不断波动而后在低于正常站立空间位置后趋于平稳, 而后恢复站立行走行为, 关节点空间位置恢复到站立时候的行为数据.
但是相反的我们可以看出传统的穿戴式检测设备如果在相同时间段内做同本实验相同的动作时候会发现当人体重复不断做下蹲的时候, 由于穿戴设备位置等原因导致无法识别下蹲运动而产生误报的问题, 设备在跌倒的时间之前系统就发出跌倒预警, 这是由于传统穿戴式设备所检测的位置很大程度影响到检测的精确性, 导致检测结果不准确.
| 表 1 模型检测实验 |
| 表 2 传统穿戴式传感器测试数据 |
从表2中可以看出传统穿戴式传感器因为存在身体特定位置的局限性所以在做例如重复下蹲运动时候会导致实验结果出现很大的误报率, 但是本实验通过三维坐标的映射关系以及父子节点的链接关系结构模型可以有效的解决传统穿戴式跌倒检测设备的误报率等问题, 并且本实验多检测的准确度在99.7%, 所以论文提出的检测方法可以精准的判断出跌倒发生的状态.
6 结论本文提出了一种基于人体模型的三维空间关节点检测人体行为状态的老人跌倒检测方法, 该方法可以将穿戴式传感器设备放置于身体任何子关节的位置, 通过穿戴式设备中内置的RLS位置传感器来实时获取当前关节点得位置数据, 在获取到行为关节点数据之后通过父子关节点关系建立父子链接的树形结构的人体模型, 将子关节点所处的二维坐标采用空间坐标映射的方法映射到三维空间形成关节点三维空间坐标, 而后对人体行为模型进行空间平面切割, 形成用于检测关节点行为活动的单元格, 然后对落于单元格内的关节点三维空间坐标进行位置预测, 通过子节点的位置预测函数预测出父节点的行为, 最后通过父子节点的位置预测来判断人体是否发生跌倒行为, 实验最终证明该方法相较于传统的穿戴式跌倒检测设备在提高跌倒精确度以及减少误报率等方面具有明显提高.
| [1] |
Harrou F, Zerrouki N, Sun Y, et al. An integrated vision-based approach for efficient human fall detection in a home environment. IEEE Access, 2019, 7: 114966-114974. DOI:10.1109/ACCESS.2019.2936320 |
| [2] |
Li DW, Yan SY, Cai X, et al. An integrated image filter for enhancing change detection results. IEEE Access, 2019, 7: 91034-91051. DOI:10.1109/ACCESS.2019.2927255 |
| [3] |
Lu N, Wu YD, Feng L, et al. Deep learning for fall detection: Three-dimensional CNN combined with LSTM on video kinematic data. IEEE Journal of Biomedical and Health Informatics, 2019, 23(1): 314-323. DOI:10.1109/JBHI.2018.2808281 |
| [4] |
Lee JS, Tseng HH. Development of an enhanced threshold-based fall detection system using smartphones with built-in accelerometers. IEEE Sensors Journal, 2019, 19(18): 8293-8302. DOI:10.1109/JSEN.2019.2918690 |
| [5] |
Cho H, Yoon SM. Applying singular value decomposition on accelerometer data for 1D convolutional neural network based fall detection. Electronics Letters, 2019, 55(6): 320-322. DOI:10.1049/el.2018.6117 |
| [6] |
Hussain F, Hussain F, Ehatisham-ul-Haq M, et al. Activity-aware fall detection and recognition based on wearable sensors. IEEE Sensors Journal, 2019, 19(12): 4528-4536. DOI:10.1109/JSEN.2019.2898891 |
| [7] |
Akagündüz E, Aslan M, Şengür A, et al. Silhouette orientation volumes for efficient fall detection in depth videos. IEEE Journal of Biomedical and Health Informatics, 2017, 21(3): 756-763. DOI:10.1109/JBHI.2016.2570300 |
| [8] |
Wang XL, Li DH, Zheng XW, et al. Research on fall detection system of wearable devices based on ELM algorithm. Proceedings of the IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC). Chengdu, China. 2019. 1008–1011.
|
| [9] |
Saadeh W, Butt SA, Altaf MAB. A patient-specific single sensor IoT-based wearable fall prediction and detection system. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2019, 27(5): 995-1003. DOI:10.1109/TNSRE.2019.2911602 |
| [10] |
Xu JY, Liu S, Lu XX, et al. A temporal adaptive access mechanism for data fusion in an IoT environment. Sensors, 2018, 18(12): 4205. DOI:10.3390/s18124205 |
| [11] |
陈鹏, 涂亚庆, 童俊平, 等. 可穿戴式跌倒检测智能系统设计. 传感器与微系统, 2017, 36(2): 114-116. |
| [12] |
尤若宁, 庄伟萍. 一种可穿戴式跌倒检测报警系统的设计. 中国医疗设备, 2017, 32(8): 28-32. DOI:10.3969/j.issn.1674-1633.2017.08.008 |
| [13] |
张云浦, 李玉榕, 陈建国. 基于MEMS传感器的可穿戴式老年人跌倒监测系统的设计. 生物医学工程研究, 2014, 33(3): 170-175, 183. |
 2020, Vol. 29
2020, Vol. 29



