许多现实世界中的复杂系统都可以使用复杂网络来描述, 例如社交网、生物网、万维网、交通网等. 复杂网络可建模为图, 其中节点表示网络中的对象, 边表示对象间的关系. 大量研究结果表明: 复杂网络通常具有小世界性和无标性等统计特性, 并呈现出社区结构等拓扑特性. 一个网络可以分成若干社区, 社区内部的节点连接相对紧密, 不同社区之间的节点连接相对稀疏[1,2]. 社区发现的目的是找出复杂网络的社区结构, 提取社区结构中的信息.
来自不同领域的研究中提出了许多不同的社发现算法, 这些算法可大致分为: 图划分的分割算法[3]、聚类算法[4-6]、基于网络动力学特性的算法[7-9]和基于目标函数的优化算法[10-14]. 其中以模块度函数(Modularity, Q)的为目标函数的优化算法是目前较为普遍的一类算法. 模块度函数Q是Newman提出的评价社区结构优劣的指标[6], 借助于该函数可将社区发现问题转化为优化问题. 如Duch[15]提出了基于模块度的极值优化算法, Guimera等[16]基于模拟退火的GA(Genetic algorithm)算法, 2008年Blondel等[17]提出的BGLL算法. 然而求最优模块度的社区结构是NP难问题, 常常用启发式算法求解. 许多启发式算法属于贪心法, 一般很难求得满意的社区划分结果, 且需要预先设定网络的社区数目. 智能优化元启发式算法作为社区发现问题的一种有效解决手段, 目前已被广泛应用求解[18-20]. Talbi等[21]提出了一种求解图划分问题的并行遗传算法, 该算法具有超线性加速特性. Bui等[22]提出了基于图划分的预处理模式从而提高遗传算法的空间搜索能力. Tasgin等[23]基于模块度使用了遗传算法进行社区发现. Gog等[24]基于种群中个体的信息分享机制提出了一种协同进化算法用于社区发现. Pizzuti[25]提出了GA-Net遗传算法, 利用了locus-based表示法和交叉操作, 该方法在操作时只考虑了该点的实际连接关系, 有效的减少了无效搜索. Gong等[26]提出了一种文化基因算法用于优化模块密度进行社区发现. Duch等[15]通过对标准差分进化算法的交叉操作进行离散化, 提出了离散差分进化算法用于社区发现. Change等[27]采用最大最小蚁群算法, 通过信息素的挥发和路径的选择进行社区的划分. 金弟等[13]通过分析模块度函数的局部单调性, 以及改进遗传算法的变异策略, 提出一种基于局部搜索的改进遗传算法. 张英杰等[14]提出了一种基于免疫差分进化算法IDDE (Immune Discrete Differen-tial Evolutiona). Said等[28]提出了基于聚类协同系数的CC-GA (Clustering Coefficient based Genetic Algorithm)算法, 该算法可用于稠密网络和稀疏网络的社区发现.
Jaya算法[29]是由Rao RV提出的一种元启发式算法, 适用于求解连续型最优化问题. 与其它元启发式算法相比, Jaya算法简单, 需要输入的参数少, 只需设置种群大小和迭代次数. 该算法通过离散化, 近年来已被应用在许多不同的组合优化问题上[30,31]. 本文针对复杂网络社区发现问题, 遵循Jaya算法的基本思想, 提出了一种离散化的算法形式称作DJaya (Discrete Jaya algorithm), 其核心思想是针对种群中个体不同的倾向性, 采取不同的更新方式,平衡全局探索性和局部搜索性来提高搜索的有效性. 在标准人造网络数据集GN Benchmark和几个典型的真实网络算例上的实验分析表明, DJaya算法能自动确定社区的数目, 且在模块度、互信息等方面表现出良好的性能[32].
1 相关工作 1.1 模块度函数不同的社区发现算法在同一复杂网络上进行社区划分时结果通常是不同的. 为了统一评价标准, Newman等提出了社区结构的模块度函数. 模块度函数易于理解且计算简单, 被广泛用来评价社区划分质量[5]. 一个社区结构的模块度
| $ Q = \dfrac{1}{{2m}}\displaystyle\sum {\left[ {{A_{ij}} - \dfrac{{{k_i}{k_j}}}{{2m}}} \right]} \delta \left( {{c_i},{c_j}} \right) $ | (1) |
其中,
基于模块度优化的社区发现算法有许多, 其中包括许多以模块度为目标函数的算法, 其典型的代表如FMM (Fast Modularity Maximization)算法[5]、LPA (Label Propagation Algorithm)算法[33]、BGLL算法[24]等贪心启发式算法, 以及近年提出的ACO (Ant Colony Optimization)[28]、LGA (Genetic Algorithm with Local search)[14]、IDDE、CC-GA等元启发式算法.
FMM算法将图中每个节点初始化为一个单独的社区, 然后选择使模块度
标签传播算法LPA是由Raghavan等提出的[34], 其基本思想是让每个节点有一个自己特有的标签, 节点会选择自己邻居中出现次数最多的标签, 如果每个标签出现次数一样多, 就随机选择一个标签替换自己原始的标签, 如此往复, 直到每个节点标签不再发生变化, 那么持有相同标签的节点就归为一个社区. 标签传播算法具有简单、高效、快速的优点, 常常和其它算法结合, 用来初始化种群, 增加种群的多样性和精度, 加快算法的收敛.
BGLL算法是一种层次性贪心算法, 它是一个两阶段过程. 第一阶段首先将每一个节点划分作为单独的社区, 然后考虑将每个节点合并到其邻接点所在的社区中, 执行能使模块度增大的合并. 第二阶段将第一阶段划分出来的社区聚合成为一个点后形成新的网络, 再在新的网络上重复以上过程, 直到网络中的结构不再改变为止.
ACO算法以网络的一个随机社区划分作为初始解, 通过编码把初始解作为路径上的初始信息素, 然后利用网络的邻接矩阵作为路径选择启发函数, 采用最大最小蚁群算法不断对模块度函数进行优化. 迭代一定次数后, 产生的路径即解码为最终的社区划分.
LGA算法以模块度Q为目标函数, 采用基于社区标识的编码方式, 然后利用标签传播法初始化种群, 采用单路交叉、局部搜索变异LMA和μ+λ选择等3个算子来探测网络社区结构.
IDDE算法的基本思想是先用标签传播法初始化种群; 然后借鉴差分进化算法基本特征, 采用随机单点变异、单路交叉和贪婪选择策略生成中间种群,最后对执行免疫克隆选择操作, 生成下一代种群. 该算法融合离散差分进化算法的全局搜索能力和免疫克隆选择策略的局部搜索能力, 增加了算法的鲁棒性.
CC-GA算法通过使用聚类协同系数来初始化种群, 以模块度为适应度函数, 利用遗传中的统一交叉和提出的变异操作进行更新种群, 该算法不需要预先知道社区的数量. 可用于稠密和稀疏网络的社区发现.
1.3 Jaya算法Jaya算法是近年来出现的一种元启发式优化算法. Jaya这个词在梵语中是胜利的意思. 因为该算法力求达到最优解从而取得胜利, 因此命名为Jaya算法[30]. Jaya算法中, 第一步是随机初始化规模大小为NP的种群, 后续每一步不断迭代, 每次迭代中要完成从一个种群更新到下一个种群的任务, 直到满足最大迭代次数为止. 每一代种群要选出最好解和最差解用于更新种群中的每个个体解. 种群中个体的更新采用下述公式:
| $ \begin{aligned} {X_i}(t + 1) =& {X_i}(t) + {r_1} \times \left( {{X_B}(t) - \left| {{X_i}(t)} \right|} \right) - {r_2}\\ &\times \left( {{X_W}(t) - \left| {{X_i}(t)} \right|} \right),\quad i = 1,2,\cdots,{N_p} \end{aligned} $ | (2) |
其中,
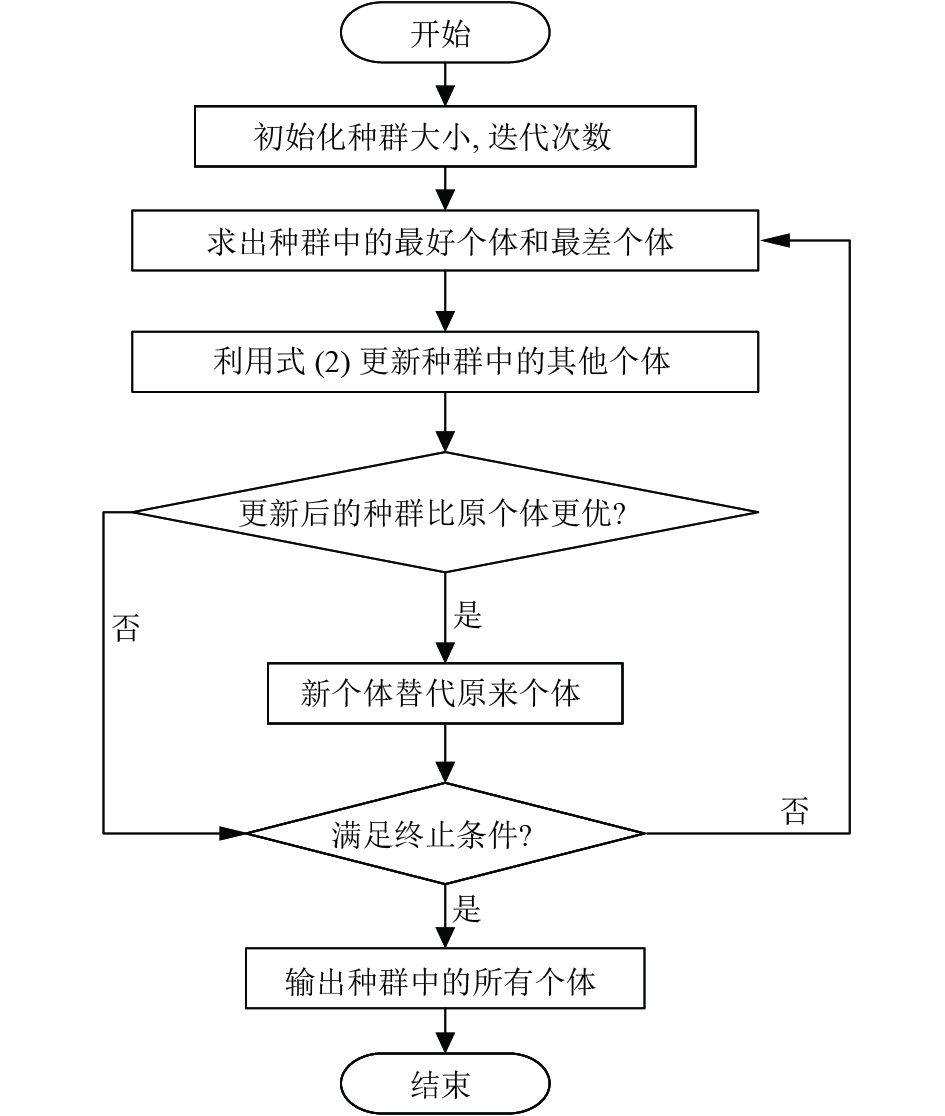
Jaya与其它元启发式优化算法相比, 简单易理解, 参数较少, 只需要设定种群的大小和迭代的次数. Jaya算法的流程图如图1.
|
图 1 Jaya算法流程图 |
2 离散Jaya的社区发现算法
在本节中, 我们主要介绍如何对Jaya算法进行离散化. 主要从社区的编码和初始化、离散化策略以及算法伪代码几方面展开.
2.1 社区结构的表示和初始化社区结构对应网络的划分, 其表示方式往往与算法相关且是影响算法效果的一个关键. 社区发现的进化类算法中, 一个社区结构对应的网络划分可以看作是一个个体. 目前有两种经典的个体表示方法[32], 一种是基于社区标识符表示法LR (Label-based Represen-tation), 另外一种是局部邻接表示LAR (Locus-based Adjacency Representation). 本文采用局部邻接表示法, 在该表示法中, 向量的元素值代表该节点的某个邻居节点的节点标识符. 如图2, 网络局部邻接表示如表1, 其对应的网络划分见图3.

|
图 2 一个网络示例 |
| 表 1 网络的局部邻接表示 |

|
图 3 表1对应的局部邻接表示所导出的网络划分 |
根据上述社区表示结构方式, 本文使用类似标签传播思想的方法进行种群的初始化. 在初始化过程中, 首先使网络中的每个节点都随机选择其中一个邻居节点, 每一次迭代中, 如果节点i的邻居节点出现的次数最多, 则该邻居节点作为节点i的值; 如果邻居节点出现的次数一样, 则随机选择一个邻居节点.
2.2 离散化策略Jaya算法适用于求解连续性的最优化的问题. Jaya算法的主要思想是通过远离最差解, 靠近最优解更新种群. 社区发现是一个离散型的组合优化问题. 当使用个体向量表示社区的一个划分时, 该向量中的每一个元素代表一个节点, 如果利用Jaya算法对个体向量更新, 如对个体向量的作差运算, 但节点之间的作差运算并无意义. 为了采用Jaya算法的思想求解社区结构划分问题, 我们需要对Jaya算法做离散化处理, 为此先引入几个概念.
(1)倾向性
为了判断种群中的个体是更靠近最优解个体还是更靠近最差解个体, 本文提出倾向性判断公式:
| $ bestGap = Q({x_{\rm best}}) - Q(x) $ | (3) |
| $ worstGap = Q(x) - Q({x_{\rm worst}}) $ | (4) |
| $ Gap = bestGap-worstGap $ | (5) |
(2)最优相似率
最优相似率即当前个体向量与最优解个体向量相同节点个数占全部元素的比率, 其计算公式如下:
| $ similarRate = \displaystyle\sum\limits_{d = 1}^n {({X_d}\Theta X_d^{\rm best})/n} $ | (6) |
其中,
(3)模块度函数的局部更新
为了使得模块度函数最大化, 我们定义一种模块度函数的局部贪心更新方式. 通过依次遍历该节点的邻居节点, 选择模块度最大化的邻居节点进行替代. 第t+1代的个体更新用式(7)表示如下:
| $ X_d^{t + 1} = {\rm{arg}}\;{\max _j}{Q}(X_d^t,j|j \in Neighbo{r_{\;d}}) $ | (7) |
其中, X表示一个个体向量解(向量的元素对应图中的节点),
(4)贪心选择
当个体更新后, 选取适应度较高的个体作为下一代的父种群个体, 即贪心选择. 该操作相当于遗传中的“优胜劣汰”, 同时和Jaya算法保持了一致的筛选策略, 对比非贪心选择策略, 即优化后的个体不进行比较直接作为下一代, 选用贪心选择策略保证了下一代种群中每一个个体都至少不会变得更差, 从而使解的平均质量更优, 加快了收敛速度.
基于上述几个概念, 下面给出Jaya算法离散化策略, 离散化的Jaya算法称作DJaya算法. DJaya算法通过式(3)~式(5) 来判断种群中每个个体是靠近种群的最优解还是最差解, 从而对种群中的个体离散化为两类. ① 对于种群中更靠近最差解的个体, 采用类似标签传播的方法依次对该个体的各个节点进行更新操作, 该操作提高了较差个体的多样性和精度, 达到了进一步远离最差解的效果, 有利于DJaya算法的全局探索性. ② 对于种群中靠近最优解的个体, 先对该个体向量采用式 (6) 计算出最优相似率, 然后基于相似率对该个体的某些节点采用式 (7) 进行局部更新, 该操作有利于加快种群的优化速度, 使整个种群更加靠近最优解, 从而有利于增强DJaya算法的局部开发性.
DJaya算法通过判定种群中个体的倾向性来平衡各个阶段的全局搜索能力和局部搜索能力, 当个体靠近最优个体解, 采取类似标签传播方法进行更新, 相当于重新定义初始解, 有利于探索出最优解, 体现了全局搜索能力; 当算法靠近最有个体解, 采取了基于局部函数的更新方法, 进一步优化了精英解, 加快了算法收敛, 体现了局部搜索能力.
(5)随机抖动
为了更进一步避免算法陷入全局较优, 我们加入了随机抖动操作, 相当于遗传算法中的变异操作, 是一种局部开发, 有利于增加搜索方向, 增大搜索空间.当连续迭代几次后种群中的个体没有得到优化, 则执行随机抖动, 即随机选择该个体节点的某个邻居节点值替代当前个体节点值. 该操作设置了一个较小的抖动率, 一方面保持原始种群的较优性, 另一方面增加多样性.
2.3 DJaya算法流程综上, 通过选取模块度为适应度函数, 采用LAR表示种群的划分和类似LPA策略进行初始化, 然后在每代种群更新中采用离散化的DJaya算法进行不断的迭代优化, 选取适应度高的个体作为下一代的父种群. 算法DJaya的描述如算法1.
算法1. DJaya算法
输入: G, M, T, R//G表示网络, M表示种群规模, T表示最大迭代次数, R表示随机抖动率
输出: Result// 网络社区结构
1. Begin
2. P←LAR进行表示, 并用LPA初始化父种群
3.
4. For i = 1: T
5. For j = 1: M
6. Gap(j)← 利用式(3)~(5)判断个体倾向性
7. If Gap(j) > 0 //靠近最差个体
8. P(new)←LPA(j) //类似标签传播法更新
9. Else //靠近最优个体
10. If rand () < similarRate ( j)//满足最优相似率
11. P(new)←利用公式(7)更新
12.
13. If rand () < R
14.
15. End For
16.
17. End For
18.
19. End
下面分析DJaya算法的时间复杂度. 假设网络中
实验平台为Windows 10系统, Intel(R) Core(TM)i5 CPU 1.8 GHz, 内存8.0 GB. 实验数据包括不同参数情况下的扩展GN Benchmark[33]人工网络 和4个经典真实网络. 实验中将DJaya算法与LPA, FMM, BGLL等经典贪心算法, 以及智能算法如ACO、LGA、IDDE、CC-GA进行比较. 为了减少统计误差, 每个算法在每个算例上独立运行20次, 取平均值作为算法运行的结果.
按照惯例, 针对人工网络, 已知其真实社区结构, 实验中仅比较各算法的标准互信息值; 对于真实的网络, 我们比较不同算法的模块度值[34].
标准互信息(Normalized Mutual Information, NMI)[35]常用来评价算法的划分结果与网络真实划分结果的吻合程度. 对于网络的的两种划分A和B, 它们之间的互信息定义如下:
| $ NMI = \frac{{ - 2\displaystyle\sum\nolimits_{i = 1}^{{C_A}} {\displaystyle\sum\nolimits_{j = 1}^{{C_B}} {{C_{ij}}\log \left( {{C_{ij}}N{/}{C_{i,}}{C_{,j}}} \right)} } }}{{\displaystyle\sum\nolimits_{i = 1}^{{C_A}} {{C_i}\log ({C_{i,}}{/}N) + \displaystyle\sum\nolimits_{j = 1}^{{C_B}} {{C_{,j}} \cdot \log ({C_{,j}}/N)} } }} $ | (8) |
其中, N表示节点个数.
为了分析DJaya算法的优化性能, 我们在扩展GN Benchmark上进行了实验分析. 该人工网络的社区结构已知, 它含有128个节点, 共划分为4个不同的社区, 每个社区有32个节点, 社区中每个节点的平均度数为16, 如表2. 网络中的混合参数
| 表 2 人工网络的参数(GN benchmark) |
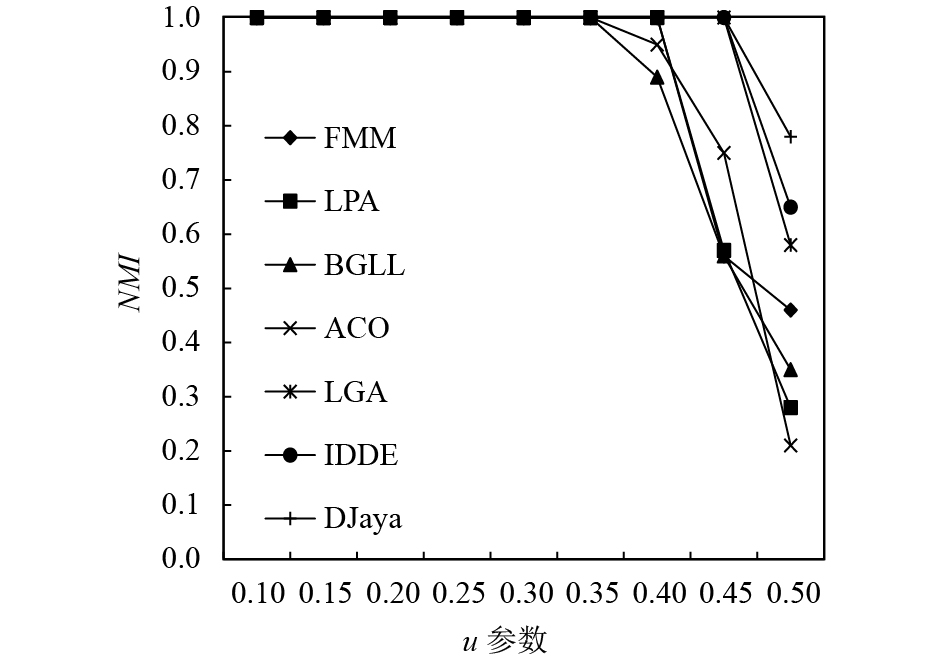
由图4可见, 当
|
图 4 各种算法划分精度的比较 |
3.2 真实网络比较实验
真实的复杂网络与人工网络相比, 有不同的拓扑属性. 这里采用了4个被广泛使用的真实网络作为实验数据集, 其点数和边数见表3. Karate[36]网络是通过对一个美国大学空手道俱乐部进行观测而构建出的一个社会网络. Dolphins[37]是由Lusseau 等使用长达7年的时间观察新西兰Doubtful Sound海峡62只海豚群体的交流情况而得到的海豚社会关系网络. Polbooks[6]是由Amazon上销售的美国政治相关书籍页面上建立起来的网络. Football[1]网络是根据美国大学生足球联赛而创建的一个复杂的社会网络.
| 表 3 4个真实网络数据的参数 |
表3中, football真实社区的划分效果与DJaya算法划分的效果图分别如图5和图6.
如图5, football对应的真实社区有12个, 图6采用DJaya算法划分的社区则有10个, 可以看出DJaya算法合并了一些较小的社区, 保持了大部分社区划分是和真实社区一致, 文献[2]认为这种划分是合理的.
表4给出了各种算法在4个标准真实网络算例上所得的模块度值. 对于算例Karate, CC-GA、LGA、DJaya都达到0.4198最优值[38]; 在算例Dolphins上DJaya算法取得了最高的模块度值; 在算例polbooks上, DJaya和LGA都达到了该数据集的理论最高值0.5272[39]; 在算例football上, LGA、IDDE、DJaya都表现良好, 达到了最优值[39]. 综上所述, 在4个算例上, DJaya算法展现出较明显优势.

|
图 5 真实的football的社区(12个社区) |
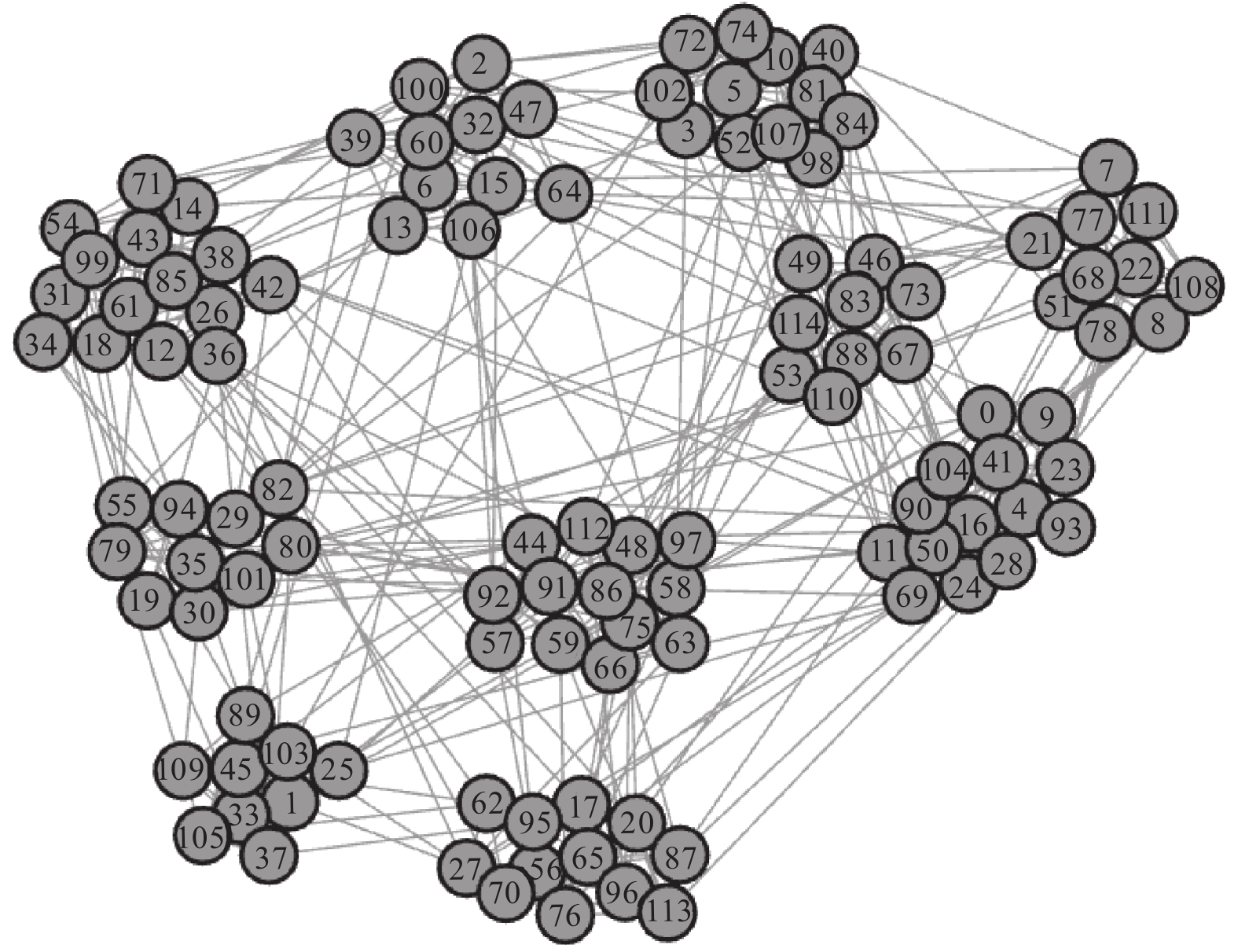
|
图 6 DJaya划分的football社区(10个社区) |
4 总结
本文提出的DJaya算法用于求解复杂网络社区发现问题, 该算法采用局部邻接表示法的编码方式对种群进行社区表示, 并用标签传播思想进行初始化, 然后借鉴连续空间Jaya算法的靠近最优解、远离最差解的基本思想, 先判断种群个体的倾向性, 针对靠近最差解采用标签传播思想更新种群, 靠近最优解采用局部模块度函数更新种群, 最后采用贪心选择策略生成下一代种群. DJaya算法实现简单, 容易理解, 具有全局搜索能力和局部开发能力. 通过在真实网络和人工网络上的实验对比发现, 该算法具有较好的优化能力和鲁棒性, 达到了较高的社区发现精度且自动确定社区个数. 该算法适用于非重叠、静态社区, 考虑到模块度作为优化函数的局限性[39], 今后将改进算法的目标函数, 或建立多目标优化函数, 同时考虑扩展算法的适应范围, 增大数据规模, 应用在重叠、动态社区发现问题.
| 表 4 各种算法在不同网络中的模块度对比 |
| [1] |
Girvan M, Newman MEJ. Community structure in social and biological networks. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. DOI:10.1073/pnas.122653799 |
| [2] |
Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Physical Review E, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 |
| [3] |
Kernighan BW, Lin S. An efficient heuristic procedure for partitioning graphs. The Bell System Technical Journal, 1970, 49(2): 291-307. DOI:10.1002/j.1538-7305.1970.tb01770.x |
| [4] |
Clauset A, Newman MEJ, Moore C. Finding community structure in very large networks. Physical Review E, 2004, 70(6): 066111. DOI:10.1103/PhysRevE.70.066111 |
| [5] |
Newman MEJ. Fast algorithm for detecting community struc-ture in networks. Physical Review E, 2004, 69(5): 066133.
|
| [6] |
Newman MEJ. Modularity and community structure in networks. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(23): 8577-8582. DOI:10.1073/pnas.0601602103 |
| [7] |
Xing Y, Meng FR, Zhou Y, et al. A node influence based label propagation algorithm for community detection in networks. The Scientific World Journal, 2014, 2014: 627581. |
| [8] |
Van Dongen S. Graph clustering by flow simulation [Ph. D. thesis]. Utrecht: University of Utrecht, 2000. 1–173.
|
| [9] |
Rosvall M, Bergstrom CT. Maps of random walks on complex networks reveal community structure. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(4): 1118-1123. DOI:10.1073/pnas.0706851105 |
| [10] |
Jia GB, Cai ZX, Musolesi M, et al. Community detection in social and biological networks using differential evolution. Proceedings of the 6th International Conference on Learning and Intelligent Optimization. Paris, France. 2012. 71–85.
|
| [11] |
Cai Q, Gong MG, Ma LJ, et al. Greedy discrete particle swarm optimization for large-scale social network clustering. Information Sciences, 2015, 316: 503-516. DOI:10.1016/j.ins.2014.09.041 |
| [12] |
Tasgin M, Herdagdelen A, Bingol H. Community detection in complex networks using genetic algorithms. arXiv: 0711.0491, 2006.
|
| [13] |
金弟, 刘杰, 杨博, 等. 局部搜索与遗传算法结合的大规模复杂网络社区探测. 自动化学报, 2011, 37(7): 873-882. |
| [14] |
张英杰, 龚中汉, 陈乾坤. 基于免疫离散差分进化算法的复杂网络社区发现. 自动化学报, 2015, 41(4): 749-757. |
| [15] |
Duch J, Arenas A. Community detection in complex networks using extremal optimization. Physical Review E, 2005, 72(2): 027104. DOI:10.1103/PhysRevE.72.027104 |
| [16] |
Guimerà R, Amaral LAN. Functional cartography of complex metabolic networks. Nature, 2005, 433(7028): 895-900. DOI:10.1038/nature03288 |
| [17] |
Blondel VD, Guillaume JL, Lambiotte R, et al. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008, 2008(10): 10008. DOI:10.1088/1742-5468/2008/10/P10008 |
| [18] |
Pizzuti C. Evolutionary computation for community detection in networks: A review. IEEE Transactions on Evolutionary Computation, 2018, 22(3): 464-483. DOI:10.1109/TEVC.2017.2737600 |
| [19] |
Cai Q, Ma LJ, Gong MG, et al. A survey on network community detection based on evolutionary computation. International Journal of Bio-Inspired Computation, 2016, 8(2): 84-98. DOI:10.1504/IJBIC.2016.076329 |
| [20] |
Liu J, Abbass HA, Tan KC. Evolutionary community detection algorithms. In: Liu J, Abbass HA, Tan KC, eds. Evolutionary Computation and Complex Networks. Cham: Springer, 2019. 77–115.
|
| [21] |
Talbi EG. A parallel genetic algorithm for the graph partitioning problem. Proceedings of the 5th International Conference on Supercomputing. New York, NY, USA. 1991. 312–320.
|
| [22] |
Bui TN, Moon BR. Genetic algorithm and graph partitioning. IEEE Transactions on Computers, 1996, 45(7): 841-855. DOI:10.1109/12.508322 |
| [23] |
Tasgin M, Herdagdelen A, Bingol H. Community detection in complex networks using genetic algorithms. arXiv: 0711.0491, 2007.
|
| [24] |
Gog A, Dumitrescu D, Hirsbrunner B. Community detection in complex networks using collaborative evolutionary algorithms. Proceedings of the 9th European Conference on Artificial Life. Lisbon, Portugal. 2007. 886–894.
|
| [25] |
Pizzuti C. Ga-Net: A genetic algorithm for community detection in social networks. Proceedings of the 10th International Conference on Parallel Problem Solving from Nature. Dortmund, Germany. 2008. 1081–1090.
|
| [26] |
Gong MG, Fu B, Jiao LC, et al. Memetic algorithm for community detection in networks. Physical Review E, 2011, 84(5): 056101. |
| [27] |
Chang HH, Feng ZR, Ren ZG. Community detection using ant colony optimization. Proceedings of 2013 IEEE Congress on Evolutionary Computation. Cancun, Mexico. 2013. 3072–3078.
|
| [28] |
Said A, Abbasi RA, Maqbool O, et al. CC-GA: A clustering coefficient based genetic algorithm for detecting communities in social networks. Applied Soft Computing, 2018, 63: 59-70. DOI:10.1016/j.asoc.2017.11.014 |
| [29] |
Rao RV. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. International Journal of Industrial Engineering Computations, 2016, 7(1): 19-34. |
| [30] |
Gao KZ, Yang FJ, Zhou MC, et al. Flexible job-shop rescheduling for new job insertion by using discrete Jaya algorithm. IEEE Transactions on Cybernetics, 2019, 49(5): 1944-1955. DOI:10.1109/TCYB.2018.2817240 |
| [31] |
Gao KZ, Zhang YC, Sadollah A, et al. Jaya, harmony search and water cycle algorithms for solving large-scale real-life urban traffic light scheduling problem. Swarm and Evolutionary Computation, 2017, 37: 58-72. DOI:10.1016/j.swevo.2017.05.002 |
| [32] |
Hruschka ER, Campello RJGB, Freitas AA. A survey of evolutionary algorithms for clustering. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2009, 39(2): 133-155. DOI:10.1109/TSMCC.2008.2007252 |
| [33] |
Lancichinetti A, Fortunato S, Radicchi F. Benchmark graphs for testing community detection algorithms. Physical Review E, 2008, 78(4): 046110. DOI:10.1103/PhysRevE.78.046110 |
| [34] |
Raghavan UN, Albert R, Kumara S. Near linear time algorithm to detect community structures in large-scale networks. Physical Review E, 2007, 76(3 Pt 2): 036106. |
| [35] |
Danon L, Díaz-Guilera A, Duch J, et al. Comparing community structure identification. Journal of Statistical Mechanics: Theory and Experiment, 2005, 2005(9): 09008. DOI:10.1088/1742-5468/2005/09/P09008 |
| [36] |
Zachary WW. An information flow model for conflict and fission in small groups. Journal of Anthropological Research, 1977, 33(4): 452-473. DOI:10.1086/jar.33.4.3629752 |
| [37] |
Lusseau D. The emergent properties of a dolphin social network. Proceedings of the Royal Society B: Biological Sciences, 2003, 270(S2): S186-S188. |
| [38] |
Aloise D, Cafieri S, Caporossi G, et al. Column generation algorithms for exact modularity maximization in networks. Physical Review E, 2010, 82(4): 046112. DOI:10.1103/PhysRevE.82.046112 |
| [39] |
Fortunato S, Barthelemy M. Resolution limit in community detection. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104(1): 36-41. DOI:10.1073/pnas.0605965104 |
 2020, Vol. 29
2020, Vol. 29



