随着制造业自动化、信息化、智能化地发展, 工业机器人的应用越来越广泛. 为了应对市场环境的变化, 企业生产车间开始大量采用搬运机器人与自动化技术提高生产效率、降低人工成本. 随着时代的变迁, 用户的需求也从“批量化”逐渐走向了“小型化”、“定制化”, 生产排成系统作为制造业的核心, 作业车间更适合当前的工业制造加工厂. 作业车间调度问题是一个典型的NP难优化问题, 通常可以描述为: 生产车间内有N个加工工件, M台加工机器, 每个工件都有特定的若干加工工序. 调度的目标是将工件合理地安排到各个加工机器以及合理地使用其它生产资源, 并合理地安排工件加工顺序与工件加工时间, 使约束条件被满足, 同时优化一些生产性能指标. 因此带有机器人制造单元的作业车间优化问题更有现实意义与应用价值, 所以如何找到可以达成生产目标的最优解是研究的中心.
作业车间调度问题普遍的的优化目标是最小化完工时间, 即在满足相应约束的前提下优化加工周期(Make-span). 然而实际生产过程中, 由于不确定性, 特别是带有存货的加工单元, 要求工件的完工时间在一个时间窗内, 而不是一个特定的时间点, 因此针对此情况的作业车间, 优化目标为最小化提前量与延迟量的总权重.
目前, 求解作业车间调度优化问题的主要方法是使用精确算法和近似算法. Caumond等[1]研究的带有搬运小车的柔性作业车间调度问题, 提出了一个混合整数线性规划的解决方法来是最小化完工时间. 张晓玲等[2]提出用正交实验的方法来设置蚁群算法在求解车间调度问题的参数. 根据对参数的设置, 调节蚁群算法的收敛速度并且得到不同的解. 杜兆龙等[3]根据柔性车间调度问题提出基于解空间距离聚类和变邻域搜索的粒子群算法. 调整关键路径上最大关键工序的机器位置来加强局部搜索能力; 并根据机器加工工序的空间距离, 采用K-means聚类得到机器加工工序“优良个体”, 加大局部搜索性能. 晏鹏宇等[4]为克服传统遗传算法在求解具有柔性加工时间的机器人制造单元调度问题时, 易出现早熟熟练、冗余迭代等缺陷, 提出了改进遗传算法. 李宏芳等[5]为了解决车间作业调度效率低的难题, 提出了一种粒子群算法的车间作业调度方法. 该方法将每个粒子代表一种作业调度方案, 以最小化加工时间作为算法的优化目标, 通过粒子群之间的协作来获得最优作业调度方案. 刘莹等[6]针对置换流水线车间调度问题进行综述,并详细地对比各种算法. 龙传泽[7]对带有机器柔性的作业车间类型多机器人制造单元调度问题, 提出了一种改进离散粒子群算法, 设计了算法的分段编码方法与两种启发式初始化方法, 并设计了粒子的局部搜索算法, 通过算例结果分析验证了算法的有效性. 申丽娟等[8]为提高车间作业优化调度的效率, 采用基于轮盘赌的方式对粒子进行编码, 运用混沌思想对粒子群基本参数进行混沌优, 加入变异操作以提高种群的多样性, 设计了一种模拟退火算法的混合粒子群优化算法. 近年来, 随着智能优化算法的发展, 来越多的算法与作业车间调度优化问题相结合在一起, 例如: 蚁群算法[9]、改进粒子群算法[10]、基因算法[11]等, 不仅得出了有效的结果, 还展现出了近似算法的优异之处.
本文提出一种改进的元启发式算法, 将文化基因算法与一种强大的邻域搜索技术(变邻域下降搜索)结合. 文化基因算法是一个将传统全局搜算算法与局部搜索算法结合在一起的算法框架, 在之前研究基础[12]上, 将遗传算法与变邻域下降搜索相组合, 在变邻域下降搜索中进一步融合多样的邻域搜索结构, 在加快文化基因算法收敛性的同时又避免陷入局部最优. 最后对带有机器人制造单元的作业车间调度问题进行仿真实验, 结果表明了该算法的有效性.
1 问题描述N个工件在M台机器上进行加工, 每个工件有特定的加工工序及顺序, 并且每个工件各工序在机器上的加工时间已知. 带有机器人制造单元的作业车间调度系统由加工站、机器人和引导网络(guidance network)3个主要部分组成. 机器人将工件从装卸载站搬运至各个加工机器, 所有工件通过装卸载站进出系统. 加工站由加工机器、输入缓冲区和输出缓冲区3部分组成. 基本流程如下: 工件j从装载站出发, 由机器人搬运至其第一道加工工序所在的加工机器Mj上进行加工, 加工完后由机器人再将其搬运至下道工序所在的机器上, 直至加工完工件j的所有工序, 由机器人搬运至卸载站完成. 每个工件j预计在时间间隔[aj, bj]之间完成, 其中aj和bj分别代表最早的到期日和最晚的到期日. 要求确定给定各工件在各机器上的加工顺序及机器人在各站之间的搬运顺序, 使某些加工性能指标达到最优.
一般作业车间调度问题需要考虑如下约束条件:
1)所有机器在t = 0时刻都可用, 所有工件在t = 0时刻都可被加工;
2)每道工序必须在指定的机器上加工, 且必须在其前一道工序加工完成后才能开始加工;
3)某一时刻,一台机器只能加工一个工件, 每个工序在加工期间不能中途停止;
4)只有一个搬运机器人(同一时刻, 机器人只能搬运一个工件);
5)一个工件在加工过程中采取平行移动方式,转移时间忽略不计或计入加工时间;
6)机器人只能在输入输出缓冲区进行装卸载.
针对带有机器人制造单元的作业车间调度问题, 目标是找到一个最优的机器人搬运顺序, 此顺序可以最小化工件完工提前量和延迟量的总权重. 参考使用文献[1]中的问题模型, 改变其目标值并加入时间窗约束.
本文中的目标函数为最小化工件完工提前量和延迟量的总权重, 可以用下列数学公式表示:
| $ Minimi{\textit{z}}e\;\alpha \displaystyle\sum {E_j} + \beta \displaystyle\sum {T_j} $ | (1) |
其中, α和β分别代表总提前量与总延迟量的权重.
时间窗约束的数学公式如下:
| $ {E_j} = \max\left( {0,{a_j} - {\rm{ }}{C_j}} \right) $ | (2) |
| $ {T_j} =\max \left( {0,{C_j} - {\rm{ }}{b_j}} \right) $ | (3) |
其中, Ej和Tj分别代表工件j的提前量与延迟量. Cj是工件j的完工时间.
2 文化基因算法文化基因算法是一种基于种群的全局搜索和基于个体的局部启发式搜索的结合体. 它是一个框架, 在这个框架下,采用不同的搜索策略可以构成不同的文化基因算法. 本文提出的元启发式算法以遗传算法为基础进行全局搜索, 结合变邻域下降搜索进行局部搜索. 融合多样的邻域结构加速整个算法的收敛性, 并且避免其陷入局部最优.
2.1 解的表示在设计元启发式方法时, 最重要的决策之一是如何表示解, 并且以一种有效的方式将它们与搜索空间联系起来. 用一个(nk×2)的矩阵表示染色体, 其中nk是每个工件的总工序数, 每个工件号在排列中出现m次. 按照从左到右的排列顺序, 工件号出现的第k次就代表这个工件的第k个加工工序. 例如, 个体[3 1 2 2 3 1 1 2 3], 每个工件有3个加工工序. 在这个例子中, 个体的第5个位置是“3”, 代表工件3, “32”表示工件3的第2个加工工序, 因为数字3出现了2次. 如果将工件号重复出现的次数作为该工件的加工工序数, 这个方法总是可行的.
2.2 全局搜索本文提出的元启发式算法以遗传算法为基础进行全局搜索, 遗传算法是一类借鉴生物界的进化规律(适者生存, 优胜劣汰遗传机制)演化而来的随机化搜索方法. 其主要包含3部分: 选择, 交叉, 变异. 首先, 所有初始解都是随机生成的, 然后计算它们的适应度值. 在生成过程中, 选择、交叉和变异被用于生成新的个体. 以下是各操作的简单描述:
选择操作采用轮盘赌选择法来选择两个个体作为双亲, 这是遗传算法和进化算法等算法中常用的一种选择方法.
交叉操作采用PTL交叉技术[13], 此交叉方法即使在两个相同双亲的情况下, 依然可以产生一对不同的子代. 在PTL交叉中, 在第一个父代中随机产生两个切割点产生一个工件序列块, 将此块移动到子代排列的右角或左角, 然后将工件序列块中出现的数字从第二个父代中删去, 将其剩余的工件操作数填充道子代中. 交叉操作完成后, 需要对工序的排列进行修复来恢复新的工件加工顺序.
变异操作在种群中引入了一些额外的变异性, 可用来增强种群的多样性. 文中使用转置变异操作: 随机产生两个位置, 将两个位置中间的操作序列倒置排列, 产生新的加工序列, 并在之后修复工件的加工工序. 通过迭代求解, 完成遗传算法, 选择最优解进入局部搜索.
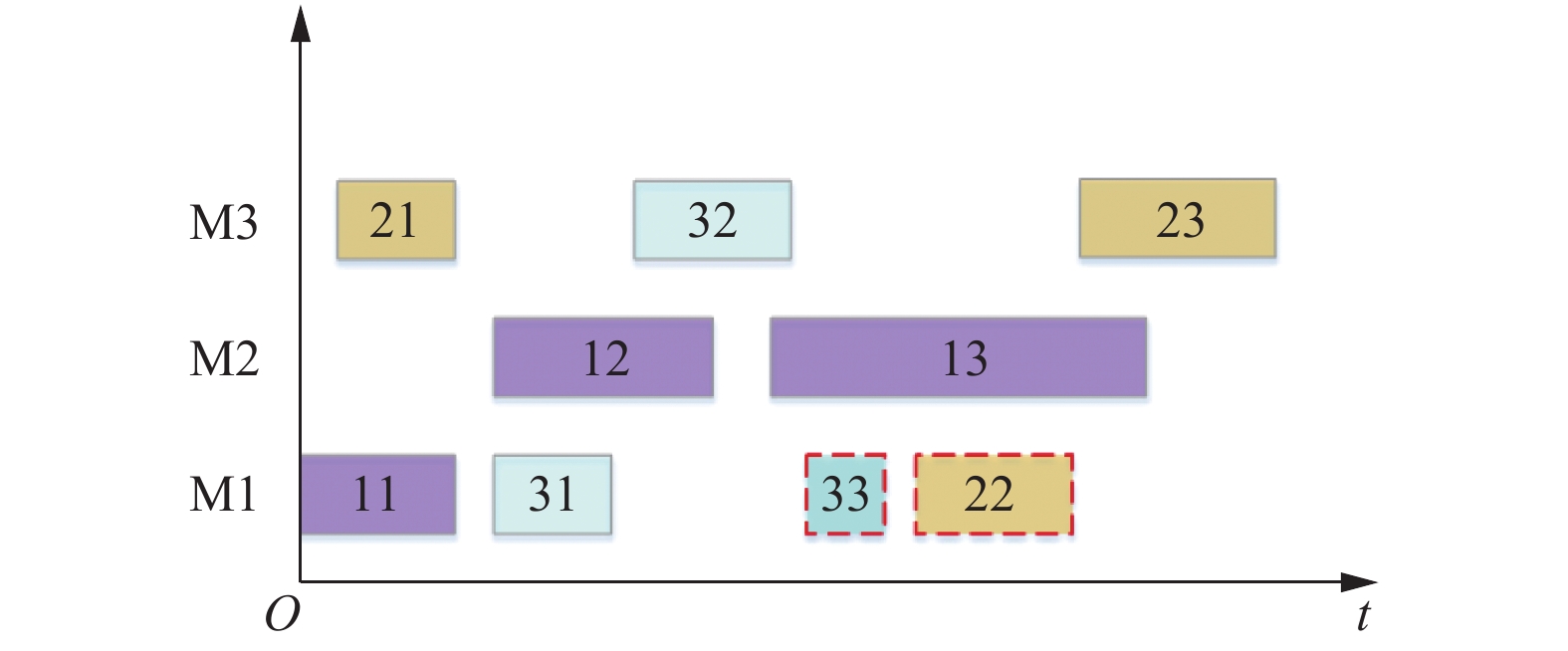
2.3 变邻域下降搜索局部搜索可以加快算法的收敛性, 本文使用变邻域下降搜索技术进行局部搜索. 其基本思想是在搜索过程中系统地改变邻域结构集来拓展搜索范围, 获得局部最优解, 再基于此局部最优解重新系统地改变邻域结构集拓展搜索范围找到另一个局部最优解的过程. 在前期的研究基础上[12], 本文提出3个邻域结构, 分别是: 段插入邻域结构, 节点插入邻域结构和根据延迟量与提前量交换工序的变换邻域结构. 从上述具有相同概率的邻域结构中随机选择一个进行局部搜索并更新. 其中, 段插入: 在解中随机产生两个位置, 将两个位置间的工序数随机插入某个工序之后. 节点插入: 在解中随机产生一个位置, 将此位置的工序数随机插入某个工序之后. 第三种邻域结构带有一定导向性, 是根据延迟量与提前量交换工序的邻域结构: 在这个方法中, 将工件划分为两组. 第一组为在到期时间窗之前完成的工件, 第二组则是在到期时间窗之后完成的工件. 对于各个加工机器上的所有加工工序, 属于第一组工件的操作移到完成时间窗右边的位置, 属于第二组工件的则移到左遍的位置. 更具体地说, 如果同一台机器包含两个不同组的工件则被视为一对, 而此机器上这一对的加工工序的位置将被互换. 例如图1, 机器M1上有4个加工操作, 假设工件3的完成时间在要求的完成时间窗之前, 工件2在完成时间窗之后, 则将工序“22”和“33”的位置进行交换.
|
图 1 邻域结构示例 |
原本“33”工序的完成使得工件3产生提前量, “22”工序使得工件2产生延迟量, 导致工件完工的提前量和延迟量的总权重过大. 经过位置交换之后, 可有效地将工件3完成时间延后, 使提前量减小, 并且使工件2的完成时间提前, 减小延迟量. 此邻域结构可以有效降低工件完工提前量和延迟量的总权重, 并找到更优的加工工序(即局部最优解)达到优化目标的要求.
2.4 改进的元启发式算法改进的元启发式算法的流程图如图2所示, 基本步骤可描述如下.

|
图 2 算法流程图 |
Step 1. 读入数据, 初始化解;
Step 2. 建立并计算目标函数, 初始化种群;
Step 3. 进入遗传算法, 进行选择、交叉、变异等操作进行迭代;
Step 4. 迭代完成后求出最优个体进入局部搜索;
Step 5. 随机选择邻域结构进行更新;
Step 6. 判断产生的新解是否大优于原最有个体的解; 是则输出新个体, 否则继续选择邻域结构进行计算;
Step 7. 输出最优个体.
3 实验结果分析本文算法以Visual Studio 2017为开发工具, 仿真实验具体过程通过C++语言进行编程实现. 通过找到加工工序及机器人搬运序列对目标函数进行计算, 得到工件完工提前量和延迟量的总权重. 再使用四中算法进行优化, 找到最优解. 选取了16组实例数据进行实验, 其中实例1至10文献[1]中的数据, 实例11至16随机生成. 每个实例包含不同数目的工件、机器与加工工序.参数aj和bj根据完工时间随机产生. 交叉概率为0.8, 变异概率为0.2, 种群规模为40. 在局部搜索的运行过程中, 搜索更新次数不超过5次. 将所提出的算法与遗传算法、传统文化基因算法、及改进文化基因算法进行比较, 每个实例数据测试10次, 并记录每个实例提前量与延迟量总权重的最优值和平均值.
最终结果如表1所示: J、M、S分别代表各实例中的工件数、机器数与总工序数. 其中, “GA*”, “MA*”, “MA-VND*”和“MA-GVND*”代表对4个算法运行10次后得到目标函数的最优值: 工件完工提前量和延迟量的总权重越小说明算法找到了更优的工件加工序列及机器人搬运序列. “MA-VND”算法为前期研究的一种启发式算法[12].
例如, 在例1中, 所得到的GA和MA算法的最优值分别为9和2, MA-VND算法及MA-GVND算法的最优值为0, 均小于“GA”和“MA”算法, 表明MA-VND算法及MA-GVND算法可以有效地找到更小的最优值: 即工件完工提前量和延迟量的总权重. “GA#”, “MA#”, “MA-VND#”和“MA-GVND#”代表对4个算法运行10次后得到的目标函数最优值取平均. 取得的平均值可以体现各算法在10次运行过程及结果中的稳定性. GA和MA算法的平均值是18.1和5.3, MA-VND算法为2.1, 所提出算法为1.9, 结果表明MA-GVND算法的稳定性较其它3种算法更优. 综合实验数据结果, 说明MA-GVND算法优于现有方法: 比遗传算法和传统文化基因算法可以更有效地达到最优目标函数值, 并且为带有机器人制造单元的作业车间调度问题提供更高质量的解.
选择实例1的结果, 使用Matlab2012编程仿真绘制甘特图(见图3), 甘特图可以描述各工件在机器上的加工顺序和机器人装卸载的搬运过程. 图中的纵坐标表示各加工机器(起始点与终止点为装卸载站), 横坐标表示加工时间轴. 例如, 实例1有3个待加工工件, 每个工件有4道加工工序. 考虑到装卸载在同一机器上进行, 即装卸/载站, 总共有5台机器. 其中 “31”是第3个加工工件的第1道加工工序, 在第3个加工机器上进行加工. 矩形的长度表示该工件此道加工工序的加工时间. 实线代表搬运机器人的带载搬运操作, 虚线代表搬运机器人的空载操作.
| 表 1 各算法数据比较 |

|
图 3 实例1甘特图 |
4 结论与展望
针对时间窗口约束下的带有机器人制造单元的作业车间调度问题, 提出了一种新的元启发式算法, 目的是最小化提前量和延迟量的总权重, 该算法结合了文化基因算法和变邻域下降搜索技术. 实验分析表明, 该算法能有效地得到机器人搬运的最佳近似序列解, 并且优于现有方法. 进一步的研究将会尝试解决带有机器人制造单元的多目标作业车间调度问题, 同时最小化完工时间与提前量和延迟量的总权重.
| [1] |
Caumond A, Lacomme P, Moukrim A, et al. An MILP for scheduling problems in an FMS with one vehicle. European Journal of Operational Research, 2009, 199(3): 706-722. DOI:10.1016/j.ejor.2008.03.051 |
| [2] |
张晓玲, 杨健, 杜英国. 基于正交实验的蚁群算法在车间调度问题中的应用. 计算机系统应用, 2010, 19(4): 152-156. DOI:10.3969/j.issn.1003-3254.2010.04.037 |
| [3] |
杜兆龙, 徐玉斌, 崔志华, 等. 柔性车间调度的解空间距离聚类和变邻域搜索粒子群算法. 计算机系统应用, 2016, 25(12): 143-148. DOI:10.15888/j.cnki.csa.005482 |
| [4] |
晏鹏宇, 车阿大, 李鹏, 等. 具有柔性加工时间的机器人制造单元调度问题改进遗传算法. 计算机集成制造系统, 2010, 16(2): 404-410. DOI:10.13196/j.cims.2010.02.182.yanpy.003 |
| [5] |
李宏芳, 郑睿颖. 粒子群算法在车间作业调度问题中的仿真研究. 计算机仿真, 2011, 28(11): 350-353. DOI:10.3969/j.issn.1006-9348.2011.11.085 |
| [6] |
刘莹, 谷文祥, 李向涛. 置换流水线车间调度问题的研究. 计算机科学, 2013, 40(11): 1-7, 22. DOI:10.3969/j.issn.1002-137X.2013.11.001 |
| [7] |
龙传泽. 柔性多机器人制造单元调度算法研究[硕士学位论文]. 广州: 广东工业大学, 2015.
|
| [8] |
申丽娟, 程子安, 李明. 车间作业优化调度问题研究. 计算机仿真, 2017, 34(6): 353-356. DOI:10.3969/j.issn.1006-9348.2017.06.076 |
| [9] |
Udomsakdigool A. Ant colony algorithm for multi-criteria job shop scheduling to minimize makespan, mean flow time and mean tardiness. International Journal of Management Science and Engineering Management, 2011, 6(2): 116-122. DOI:10.1080/17509653.2011.10671153 |
| [10] |
毛志慧, 王艳, 纪志成. 多目标柔性车间调度的文化基因非支配排序粒子群算法. 计算机系统应用, 2015, 24(10): 155-161. DOI:10.3969/j.issn.1003-3254.2015.10.026 |
| [11] |
Kundakcı N, Kulak O. Hybrid genetic algorithms for minimizing makespan in dynamic job shop scheduling problem. Computers & Industrial Engineering, 2016, 96: 31-51. DOI:10.1016/j.cie.2016.03.011 |
| [12] |
Li XH, Yang Y, Yang X, et al. A metaheuristic to solve a robotic cell job-shop scheduling problem with time window constraints. Proceedings of the 2019 4th International Conference on Mathematics and Artificial Intelligence. New York, NY, USA. 2019. 128–132.
|
| [13] |
Pan QK, Tasgetiren MF, Liang YC. A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem. Computers & Operations Research, 2008, 35(9): 2807-2839. DOI:10.1016/j.cor.2006.12.030 |
 2020, Vol. 29
2020, Vol. 29



