2. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
3. 沈阳高精数控智能技术股份有限公司, 沈阳 110168
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. Shenyang Golding NC Technology Co. Ltd., Shenyang 110168, China
我国扶贫开发工作最初起源于20世纪80年代中期, 经过近几十年的不懈努力, 取得了令人瞩目的成就. 经济社会快速发展, 人们的生活水平不断提高, 但是, 长期以来, 贫困居民的底数不清, 情况不明, 扶贫的针对性不强等问题比较突出. 国外BPS使用CAPI来进行贫困状况调查, 但是也只是针对少数地区. 在国内, 对于当地贫困人口的统计大多仍按照传统方式进行贫困数据收集, 近些年开始进行建档立卡工作. 对于进行贫困分类, 国外专家提出K-均值聚类法评估贫困等级[1]; Yu BL等利用NPP-VIIRS数据采用线性回归模型讨论了ALI值和IPI值的关系进而进行贫困分类[2]; Jean N等通过训练卷积神经网络结合高分辨率卫星图像来实现贫困户识别[3]; 李雪等提出了多层次模糊系统方法进行贫困分类[4]; 徐姝婧等提出了基于神经网络模型的方法实现贫困分类[5]. 对于上述专家提出的方案, K-均值聚类方法无法保证待归类元素找到最佳分类; 回归分析法虽然考虑到了因素间的相互依赖和相互影响关系, 但是实验次数过于冗繁且NOAA/NGDC发布的NPP-VIIRS数据存在很多噪声会影响实验结果; 模糊系统方法在指标集较大时, 会出现超模糊现象, 无法区分隶属度; 神经网络虽然具有高度自学和自适应能力, 但是它黑匣子的性质使得结果的可解释性不强, 不利于后续的扶贫分析. 综上所述, 建立一个科学, 多维, 全面的评价系统尤为重要. 本文以录入的辽宁省某地区的家庭信息为依据, 提出了基于REAHCOR-GBDT的贫困等级评价模型, 为当地精准扶贫工作顺利开展提供了更有利的保障.
1 贫困等级评价模型构建过程算法介绍 1.1 特征选择算法REAHCOR随着时代的发展, 庞大的数据集应运而生, 数据的维度和复杂性也在不断增长, 如何从大量繁琐的信息中筛选有用的信息, 构造一个好的模型, 提取关键特征显得更为迫切. 特征选择是指从一堆与目标变量相关的, 冗余的, 无关的数据中选择出分辨能力高的特征作为最优特征子集, 从而提高分类模型的准确度. 丁雪梅等介绍了改进的ReliefF算法进行无监督特征选择[6]. 李叶紫, 张尧等提出了关于互信息的特征选择来提高机器学习算法的准确率[7,8]. 李娜娜分析了影响贫困因素[9]. 本文采用的Filter算法具有速度快的优势且独立于后续学习算法, 其中ReliefF是公认效果不错的一种过滤式算法[6], 但是考虑到ReliefF不能够很好的去除冗余特征以及贫困信息分类独有的特点, 本文提出采用ReliefF算法结合层次分析法和相关度分析法来完成特征选择的方法, 即REAHCOR特征选择算法. 该方法包含以下3个阶段, 分别如下:
(1) ReliefF算法会赋予每个特征不同的权重, 依据是每个特征与类别标签的相关性有大有小, 当计算出的特征权重值大于某个阙值时, 说明它对类别标签的影响程度强, 我们保留. 反之, 说明其影响程度弱, 该特征会被删除. 权重的大小反映了该特征值区分同类近邻样本和不同类近邻样本的能力. ReliefF算法的运算过程为从训练集中随机的选取一个样本a, 然后比较样本a同类的b个近邻样本与不同类的另外b个近邻样本在某个特征的距离. 通过规定次数的迭代, 计算出所有特征的权重平均值. 其权重更新公式如下:
| $\begin{aligned} W_P^{i + 1} =& W_P^i - \displaystyle\sum\limits_{j = 1}^k {\dfrac{{diff\left( {p,x,{H_j}\left( x \right)} \right)}}{{m \cdot k}}} \\ &+ \displaystyle\sum\limits_{C \ne class\left( x \right)} {\dfrac{{\dfrac{{P\left( C \right)}}{{1 - P\left( {class\left( x \right)} \right)}}\displaystyle\sum\limits_{j = 1}^k {diff\left( {p,x,{M_j}\left( x \right)} \right)} }}{{m \cdot k}}} \\ \\ \end{aligned} $ | (1) |
(2) 在上一步得出相关特征之后, 考虑到贫困信息的复杂性和多层次性, 继而引入认可度较高的层次分析赋权法继续为特征定量权重. 其中在进行一致性指标计算时公式如下:
| $CI = \dfrac{{{\lambda _{\max }} - n}}{{n - 1}}$ | (2) |
在进行一致性比率CR计算时公式如下:
| $CR = \dfrac{{CI}}{{RI}}$ | (3) |
在计算总的层次排序时检验一致性公式如下:
| $CR = \dfrac{{{a_1}C{I_1} + {a_2}C{I_2} + \cdots+ {a_m}C{I_m}}}{{{a_1}R{I_1} + {a_2}R{I_2} + \cdots+ {a_m}R{I_m}}}$ | (4) |
(3) 采用特征间冗余度度量的相关性分析法进行特征选择. 该方法的主要思想是通过度量属性之间的相关度来衡量它们之间的冗余性. 相关度越大, 冗余度也就越大. 任江涛等介绍了基于相关性分析的选择算法可以作为一种借鉴[10]. 在本研究中, 连续型数值需进行离散化处理, 然后采用信息论中的熵概念进行度量. 信息熵的定义公式如下:
| $H\left( X \right) = - \sum\limits_i {P\left( {{x_i}} \right)} {\log _2}\left( {P\left( {{x_i}} \right)} \right)$ | (5) |
已知随机变量Y后X的信息熵定义公式如下:
| $H\left( {X\left| Y \right.} \right) = - \sum\limits_j {P\left( {{y_j}} \right)} \sum\limits_i {P\left( {\left. {{x_i}} \right|{y_j}} \right)} {\log _2}\left( {P\left( {{x_i}\left| {{y_j}} \right.} \right)} \right)$ | (6) |
如果Y和X是相互独立的, 即H(X|Y)的结果值与H(X)的结果值相同, 那它们的相关度为0; 如果Y和X有相关性, 那么X和Y之间的互信息值越大, 它们的相关性就越强. 由此信息增益值IG(X|Y)(也称变量x, y之间的互信息)公式如下:
| $IG\left( {X\left| Y \right.} \right) = H\left( X \right) - H\left( {X\left| Y \right.} \right)$ | (7) |
另外, 相关度关于变量x, y是对称的, 所以对信息增益进行归一化处理, 公式如下:
| $SU\left( {X,Y} \right) = 2\frac{{IG\left( {X\left| Y \right.} \right)}}{{\left[ {H\left( X \right) + H\left( Y \right)} \right]}}$ | (8) |
本文提出的 REAHCOR方法首先运行ReliefF算法进行特征初筛, 该算法通过计算得到每个特征的权重Wi, 将Wi值大于过滤阈值的特征保留下来, 放入到一个初始状态为空的集合U中. 然后将集合U中的特征采用层次加权法对贫困家庭指标进行定性与定量判断并把得到的权重值放入到初始为空的集合S中. 将集合U中的两两特征采用相关性分析法进行冗余度度量, 将其结果集中冗余度大于冗余阙值的两特征中在集合S里权值较小的特征删除, 选出最终需要的特征子集, 这些被选出的特征都是和类别标签相关性很强的一些特征. 上述算法的优点是: 通过使用计算效率比较快而且对数据大小和类型没有限制的过滤式ReliefF算法求出那些与目标属性不相关的特征, 然后与层次分析法和相关性分析法相结合共同解决问题. 很好的规避了ReliefF算法不能去除冗余特征的缺点, 同时能够依据贫困信息多维度多层次的特点, 将人的主观经验和客观事实相结合, 兼顾定性与定量分析, 更加贴近事实的去解决问题, 灵活性更强. 该方法与单纯使用ReliefF或Wrapper等算法相比, 可靠性高并且冗余度少, 不依赖后续学习方法, 同时继承了ReliefF算法计算速度快的优点, 减少了盲目性和不确定性, 能够得出具有科学化且性能优的特征参数子集.
1.2 GBDT算法在监督学习的算法中, 我们都希望训练出的模型是一个各方面稳定性都表现良好的模型, 但是现实却往往差强人意, 得出的模型要么方差太大导致鲁棒性不强, 要么具有较高的偏置. 而集成学习的思想就是让一些弱学习器的方差或者偏置结合起来, 从而获得比单一学习器泛化性能更好的模型. 目前集成学习的策略分为两大类, 一类是学习器与学习器之间相互独立的Bagging策略, 一类是用下一个学习器拟合上一个学习器残差的Boosting策略[11]. 由于随机森林的取样策略具有方差较小, 偏差较大的特点, 所以它对于基学习器的准确度要求比较严格. 而Boosting策略则可以减小模型的偏差, 通过逐步提升的方法使最终模型变得更加优秀. 因此本文模型的构建采用基于梯度提升技巧的GBDT算法. 算法流程如算法1所示.
算法1. Lk-TreeBoost
Fk0(x) = 0, k = 1, K
For m = 1 to M do:
For k = 1 to K do:
endFor
endFor
2 实验分析本文提出的贫困等级评价模型分为4个步骤实现, 如图1所示. 首先对采集到的数据进行预处理, 主要包括空值数据的处理、噪声数据的处理等数据规约, 数据变换过程. 接着将处理好的数据集采用本文提出的REAHCOR特征选择算法求出最优特征子集, 然后运用GBDT算法进行贫困分类. 最后对实验结果进行比对分析, 验证本文研究方法的有效性.

|
图 1 贫困等级评价模型构建 |
2.1 数据采集
本文数据来源于实验室项目“精准扶贫数据分析系统”, 数据集中包含了辽宁省某地区近万户人口的家庭信息.
2.2 数据预处理将非贫困, 一般贫困, 极度贫困这3种贫困类别作为模型目标值, 对家庭信息、当地扶贫政策和当地经济发展状况等信息进行筛选和归纳. 将家庭收入、家庭消费、食品支出、水源污染、饮水方式、教育水平、失学状况、参加合作医疗情况、生病是否能及时就医、脆弱性、卫生设施、居住环境、房屋数量等信息进行数据清洗、变换和整合, 其中对缺失值用区间变量的平均值或中值填充, 对于异常值和大量丢失的信息采用舍弃的方式来加快算法的执行速度, 对家庭收入, 用电量等特征采用MIN-MAX方法进行归一化.
2.3 特征选择贫困信息数据具有庞大而复杂的特性, 如果不加以处理, 可能会出现维度灾难. 一个好的特征选择算法, 可以从原始特征子集中选取出利用性最优的特征子集, 能够去除冗余性强的, 选取对分类结果影响最大的特征. 基于传统的过滤式(Filter)特征选择算法, 本文提出的REAHCOR算法继承了过滤式(Filter)算法运行速度快, 独立于后续模型的优点外, 又将特征依据层次性和冗余度进行优化选取, 弥补了原先算法分类性能较差的不足.
根据本文提出的REAHCOR算法, 在进行特征选取时计算出每个特征和类别的相关性估值. 最后按照估值高低进行排序, 选出最优特征子集如下: 家庭净收入、家庭负债情况、家庭受资助情况、住房数量、是否参加医疗保险、成年人受教育年限、卫生设施、适龄儿童是否在学、劳动力人数、身体是否患病、耐用消费品资产数量、生活用电量、取水方式、娱乐方式.
2.4 模型预测本文模型预测的标签分为非贫困, 一般贫困, 极度贫困3类, 根据有效的特征对模型结果进行分类. 本文验证模型的有效性从两个方面进行切入: (1) 验证REAHCOR算法的有效性; (2) 验证整体模型的有效性.
(1) 验证REAHCOR算法的有效性
在实验中选用ReliefF和FCBF算法与本文提出的REAHCOR算法进行性能比对. 在分类器的选择上, 使用Boosting算法中的GBDT算法, 并分别结合以上3种特征选择算法进行分类预测, 从而验证REAHCOR算法的有效性.
(2) 验证整体模型的有效性
首先使用本文提出的REAHCOR算法进行特征选取, 然后将选出的特征子集分别用在GBDT算法和随机森林算法中进行分类预测. 经过对比, 验证GBDT算法对本领域研究范围的有效性.
2.5 评价标准对于一个模型的好坏, 除了评价实验估计方法, 还需要衡量这个模型的泛化能力, 在分类任务中, 可以用错误率与精度、查准率、查全率与F1、代价敏感错误率和代价曲线、ROC与AUC等进行性能度量. 本实验采用查全率、查准率和F1值进行评判.
| $precision = \frac{{TP}}{{TP + FP}}$ | (9) |
| $recall = \frac{{TP}}{{TP + FN}}$ | (10) |
| $F1 = \frac{{2 * precision * recall}}{{precision + recall}}$ | (11) |
其中, TP代表真正例(true positive), FP代表假正例(false positive), FN代表假反例(false negative). 另外还有一个TN代表真反例(true negative), 并且有TP+FP+TN+FN等于样例总数. F1是基于查准率与查全率的调和平均.
2.6 实验分析(1) 在特征选择对比实验中, ReliefF算法通过迭代规定次数内样本与同类近邻样本和不同类近邻样本的距离, 筛选权值高的特征作为特征子集, FCBF算法采用后向顺序搜索策略进行快速的选取最优特征子集. 表1中展示了贫困数据集按照以上3种方法进行特征选择, 然后将得到的结果使用GBDT算法进行分类, 对结果采用交叉验证的方法进行比较, 筛选出的特征个数用Num表示.
| 表 1 基于不同特征选择算法的贫困模型结果对比 |
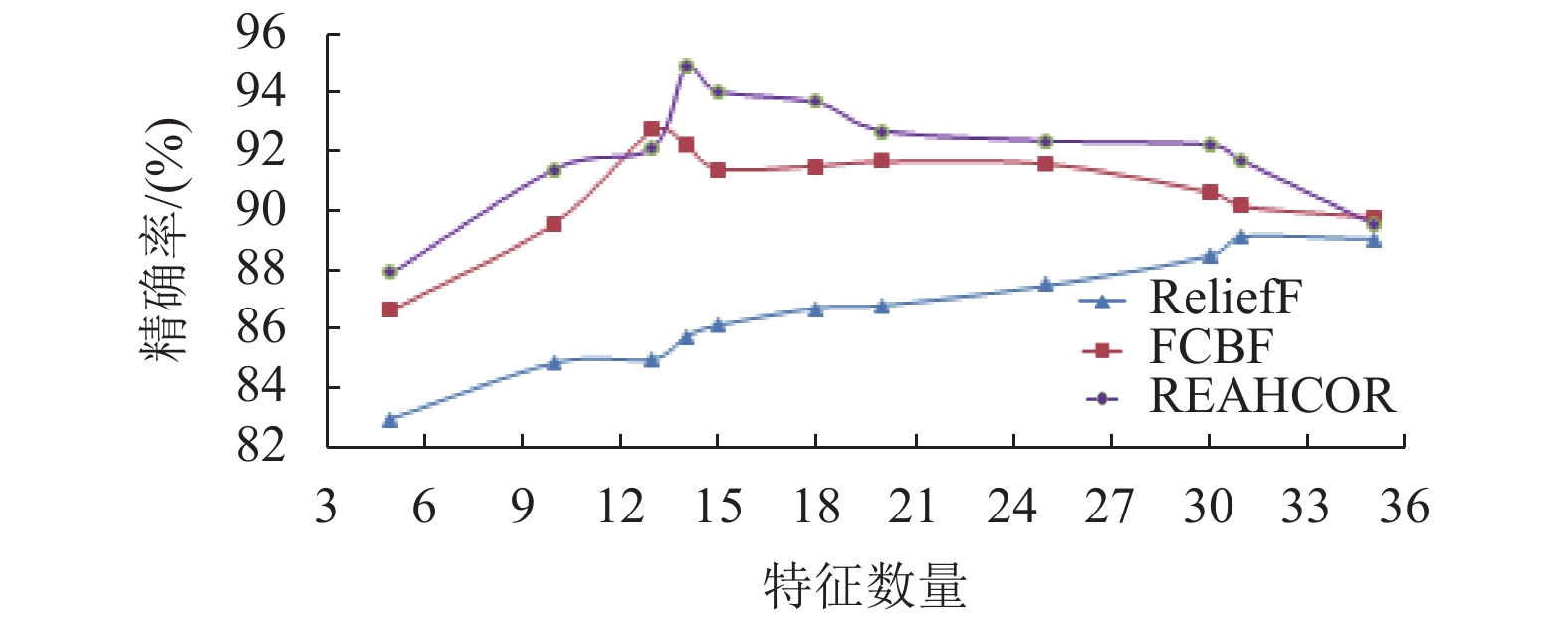
从表1和图2可以得出, 本文提出的REAHCOR特征选择算法的分类精度可以达到94.86%, 查全率为92.37%, F1值为93.60%, 分类效果优于其他两种, 在特征数量较少时ReliefF算法表现效果最差, 随着特征数量的增多其出现上涨趋势, 但是由于选出的特征冗余度大导致效果不理想, 所以其在降维方面的性能比较低. FCBF在降维方面表现稍好, 在特征数量为13时分类精度达到92.72%, 但是不如REAHCOR整体表现效果好.
|
图 2 不同特征选择算法效果对比 |
(2) 使用随机森林和GBDT算法对测试集进行分类结果的性能比较如表2所示.
| 表 2 GBDT和随机森林分类结果对比 |
从表2可以得出, 两种分类器在同一特征子集中有不同的表现, GBDT在precision, recall和F1值方面都优于随机森林算法.
3 总结本文以农村家庭信息数据为背景, 提出了基于REAHCOR的特征选择算法, 并应用到具有较高分类准确度的GBDT分类器中, 取得了分类效果较优的评价模型. 创新性提出的REAHCOR算法既可以对庞大的数据特征集进行降维, 也可以保证降维之后特征具有很强的分类能力, 整体模型的评估效果也得到验证, 具有稳定性好、灵活性强的优势. 在实际应用方面, 只要输入相关的特征数据, 就可以得到家庭贫困等级程度的信息, 对于精准识别贫困户, 帮助政府解决民生问题起到了积极的导向作用.
| [1] |
Sarwosri, Sunaryono D, Akbar RJ, et al. Poverty classification using analytic hierarchy process and k-means clustering. Proceedings of 2016 International Conference on Information & Communication Technology and Systems. Surabaya, Indonesia. 2016. 266–269.
|
| [2] |
Yu BL, Shi KF, Hu YJ, et al. Poverty evaluation using NPP-VIIRS nighttime light composite data at the county level in China. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3): 1217-1229. DOI:10.1109/jstars.2015.2399416 |
| [3] |
Jean N, Burke M, Xie M, et al. Combining satellite imagery and machine learning to predict poverty. Science, 2016, 353(6301): 790-794. DOI:10.1126/science.aaf7894 |
| [4] |
李雪, 刘洋, 叶伟铭. 基于多层次模糊系统的贫困等级认定模型. 中国新技术新产品, 2008(9): 99-101. DOI:10.13612/j.cnki.cntp.2008.11.013 |
| [5] |
徐姝婧, 陆一啸, 徐嘉瑞. 基于机器学习的贫困户识别指标体系模型研究. 上海立信会计金融学院学报, 2019(4): 108-120. DOI:10.13230/j.cnki.jrsh.2019.04.011 |
| [6] |
丁雪梅, 王汉军, 王炤光, 等. 基于改进ReliefF的无监督特征选择方法. 计算机系统应用, 2018, 27(3): 149-155. DOI:10.15888/j.cnki.csa.006243 |
| [7] |
李叶紫, 周怡璐, 王振友. 基于互信息的组合特征选择算法. 计算机系统应用, 2017, 26(8): 173-179. DOI:10.15888/j.cnki.csa.005891 |
| [8] |
张尧. 基于互信息的特征选择方法研究[硕士学位论文]. 西安: 西安理工大学, 2019.
|
| [9] |
李娜娜. 中国农村多维贫困研究[硕士学位论文]. 太原: 山西财经大学, 2012.
|
| [10] |
任江涛, 黄焕宇, 孙婧昊, 等. 基于相关性分析及遗传算法的高维数据特征选择. 计算机应用, 2006, 26(6): 1403-1405. |
| [11] |
魏仕轩, 王未央. SVM和集成学习算法的改进和实现. 计算机系统应用, 2015, 24(7): 117-121. |
 2020, Vol. 29
2020, Vol. 29



