2. 山东省智能建筑技术重点实验室, 济南 250101
2. Shandong Provincial Key Laboratory of Intelligent Buildings Technology, Jinan 250101, China
随着通信技术的日益更新, 电信产业获得了迅速发展. 现如今, 我国已经拥有世界上最大的通信网络和最多的用户数量. 由于网络规模的扩大和数据量的急剧增加, 对于智能化网络优化的需求在逐步提高[1]. 为了解决规模庞大且复杂多样的移动通信网络带来的各类问题, 国内外许多学者针对机器学习在网络优化中的应用进行了大量研究.
王西点等探究了人工智能在网络运维中的应用, 并列举了多种机器学习应用的例子[2]. 张喆利用k均值聚类算法对小区进行聚类成多个典型场景, 之后对于不同聚类场景的小区可以实现自动推荐LTE网络参数配置方案[3]. Kibria等也对下一代的无线网络及优化中的大数据分析、机器学习和人工智能进行了研究和预测[4]. 对于网络优化中的质差小区检测, 众多学者展开了更为深入的研究. 周鹏将质差小区和异常小区联系起来, 使用改进的局部异常点(LOF)检测算法, 提高了检测质差小区的正确率[5]. 曾雨桐提出用层次聚类方法对小区性能进行划分, 定位到性能较差的小区后聚类分析质差小区各项指标之间的关联度, 从而针对性地制定优化方案[6]. 王希将概率神经网络应用于LTE网络根因定位分析中, 实现了LTE质差小区的自动化分析[7]. 然而, 这些研究鲜有基于机器学习对路测数据进行分析处理. 路测是检测阶段的有效手段, 能从实际网络中获得充足的数据[8]. 目前对于路测数据的分析主要依赖于网络优化工程师的个人经验进行判断, 准确率不高、效率低下.
为了解决上述问题, 本文针对路测数据, 提出了一种基于距离的四维特征的质差小区检测方法. 首先对路测数据进行分析处理, 将距离因素引入路测分析中, 设计提取了基于距离的四维特征. 然后采用聚类算法和人工判断相结合的方式对路测数据进行标定, 并通过机器学习算法对小区进行优劣划分. 将距离因素引入路测分析中, 解决了采用单一指标判断方式不够准确的问题, 更加贴合实际, 在提高网络优化效率、降低成本等方面具有重要意义.
1 数据准备 1.1 数据选择路测(Drive Test, DT), 是指测试人员在汽车中, 持专业的测试仪器对整段路段的无线信号情况进行测试. 传统的路测分析需要对网络参数进行采集和数据分析, 找出影响网络质量的因素, 并制定优化方案[8]. 主要可以获得以下数据: 服务小区信号强度、小区识码、手机所处的地理位置、呼叫管理等值.
研究采用了某市2016年部分路测数据, 该数据采集自117个小区, 共78 613条数据. 部分原始数据如图1所示. 选择的路测数据参数为: 基站小区的经纬度信息、信号点的经纬度信息, 信号点的参考信号接收功率(Reference Signal Receiving Power, RSRP)、信号与干扰加噪声比(Signal to Interference plus Noise Ratio, SINR)、物理小区标识(Physical-layer Cell Identity, PCI). RSRP是指在一个符号内承载参考信号的所有资源粒子上接收到的信号功率的平均值, 它是LTE 网络中可以代表无线信号强度的关键参数以及物理层测量需求之一. SINR可以被认为“信噪比”, 是指接收到的有用信号和干扰信号的强度的比值. SINR的数值大小, 可以反映出信号点的噪声情况. PCI是用于区分不同小区的无线信号[9]. 但PCI值在整个网络中并不唯一. 采用PCI值的原因是这片区域小区的PCI值没有重复, 若有重复, 应更换为演进通用陆地无线接入网络小区标识(E-UTRAN Cell Identifier, ECI), 保证所用数据中的小区在这片区域的唯一性.
1.2 数据预处理由于路测数据中存在缺失值、乱码等问题, 会导致错误的处理结果, 使得算法无效或者远离期望.
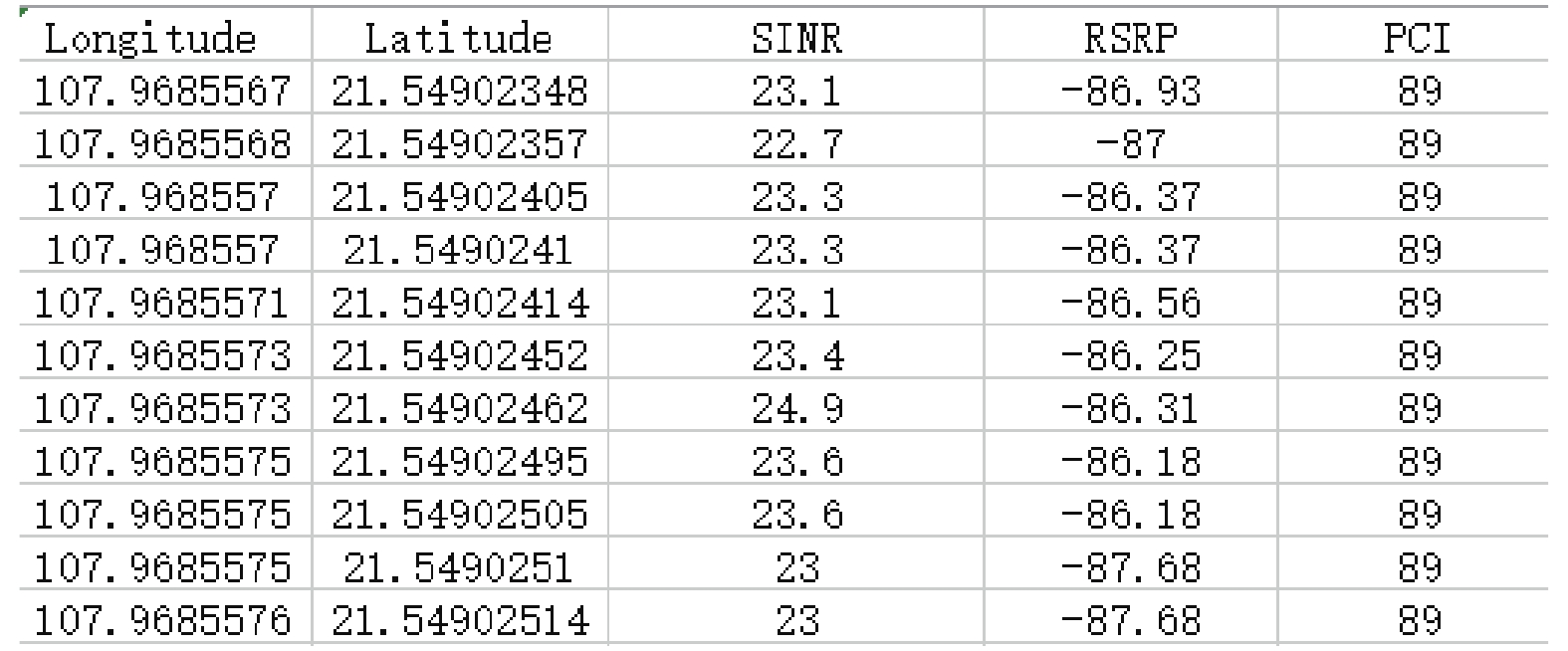
本文所提取的数据中存在着缺失值(如图1所示), 乱码(如图2所示)等问题, 需要对原始数据进行预处理. 经典的处理方法有: 删除, 均值替换等方法. 因为含缺失值、乱码值的对象与信息表中的数据量相比相对较小, 所以采用了删除元组法对数据进行处理, 即将含有缺失值、乱码值的记录删除. 最终得到68 311条数据, 预处理后的部分数据如图3所示.
1.3 特征提取预处理后的数据是以一个数据点的信息作为一条对象, 在以小区为单位的质差小区检测中, 不具有类别的可分性. 因此, 进行特征提取可以将原始特征转换为一组具有明显物理意义或者统计意义的特征, 得到可分性更大的、更利于识别的特征数据. 根据人工网优判断的经验, 进行统计特征提取.
传统质差小区的判定主要是根据路测数据中的两个指标: RSRP和SINR的采样概率. 根据规定, 在覆盖区域内, TD-LTE无线网络覆盖率若满足RSRP > –105 dBm的概率小于或等于95%, 则说明小区覆盖情况较差, 为质差小区; 若满足SINR>–1.6 dBm的采样概率小于或等于95%, 则说明小区干扰较多, 同样为质差小区.
因为信号强度随着距离的增加而逐渐衰减, 所以距离小区基站较远的区域, 其信号接收功率比距离基站较近的区域的信号接收功率弱. 由于相邻小区的信号影响, 使得小区边缘的区域接收到的干扰比小区内部的区域接收到的干扰大. 所以单一的指标不能很好的反映实际问题. 在这种情况下, 对于质差小区的判断不能只依靠覆盖率这一指标, 还应当考虑到信号点位置的影响. 因此在本研究中, 引入了信号点距离的因素, 对于距离基站较远的信号点, 可以根据实际情况, 将判断的阈值设置一个合适的比近区信号点判断阈值低的数值.

|
图 1 部分原始数据图 |

|
图 2 乱码数据图 |
|
图 3 预处理后的部分数据图 |
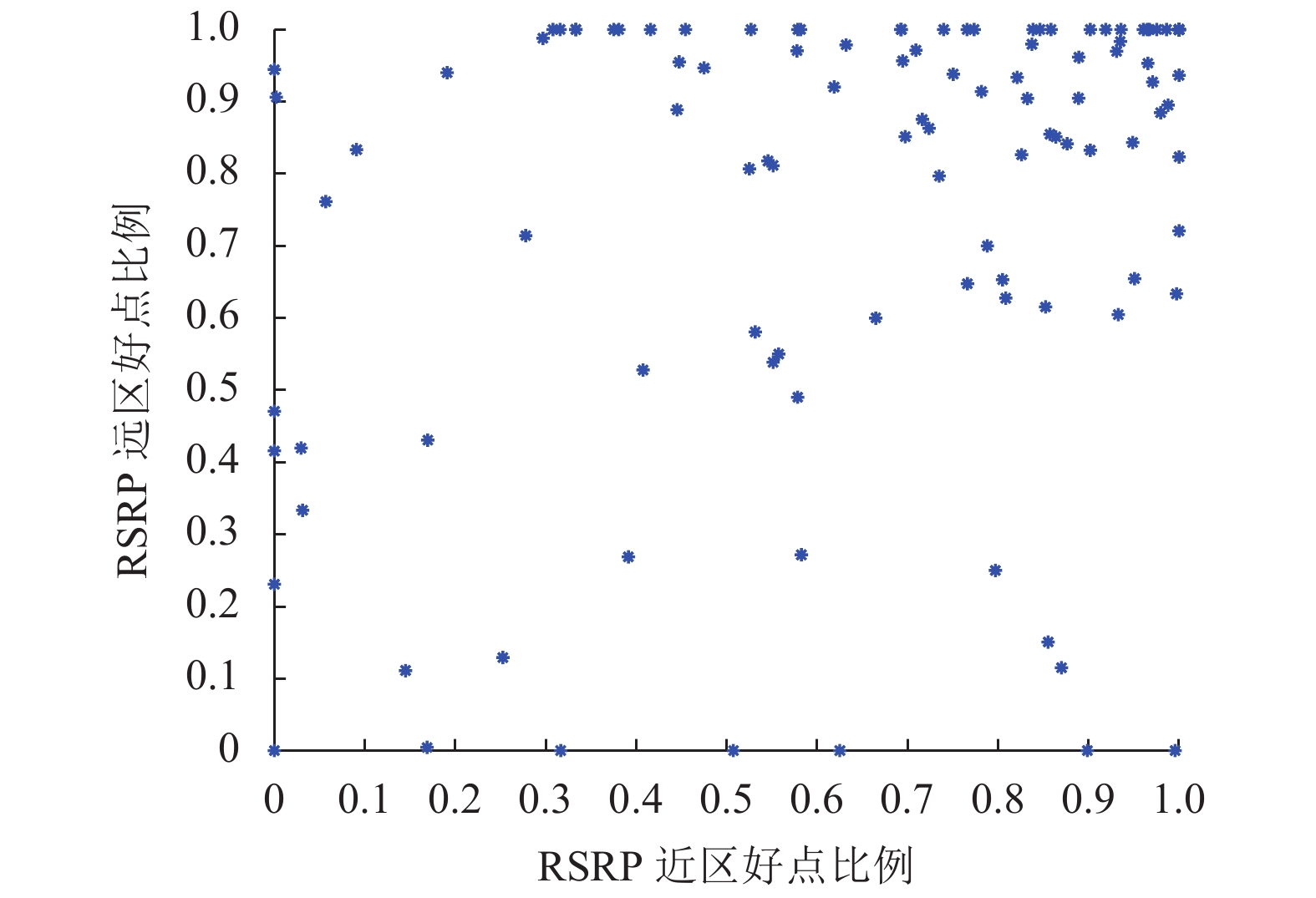
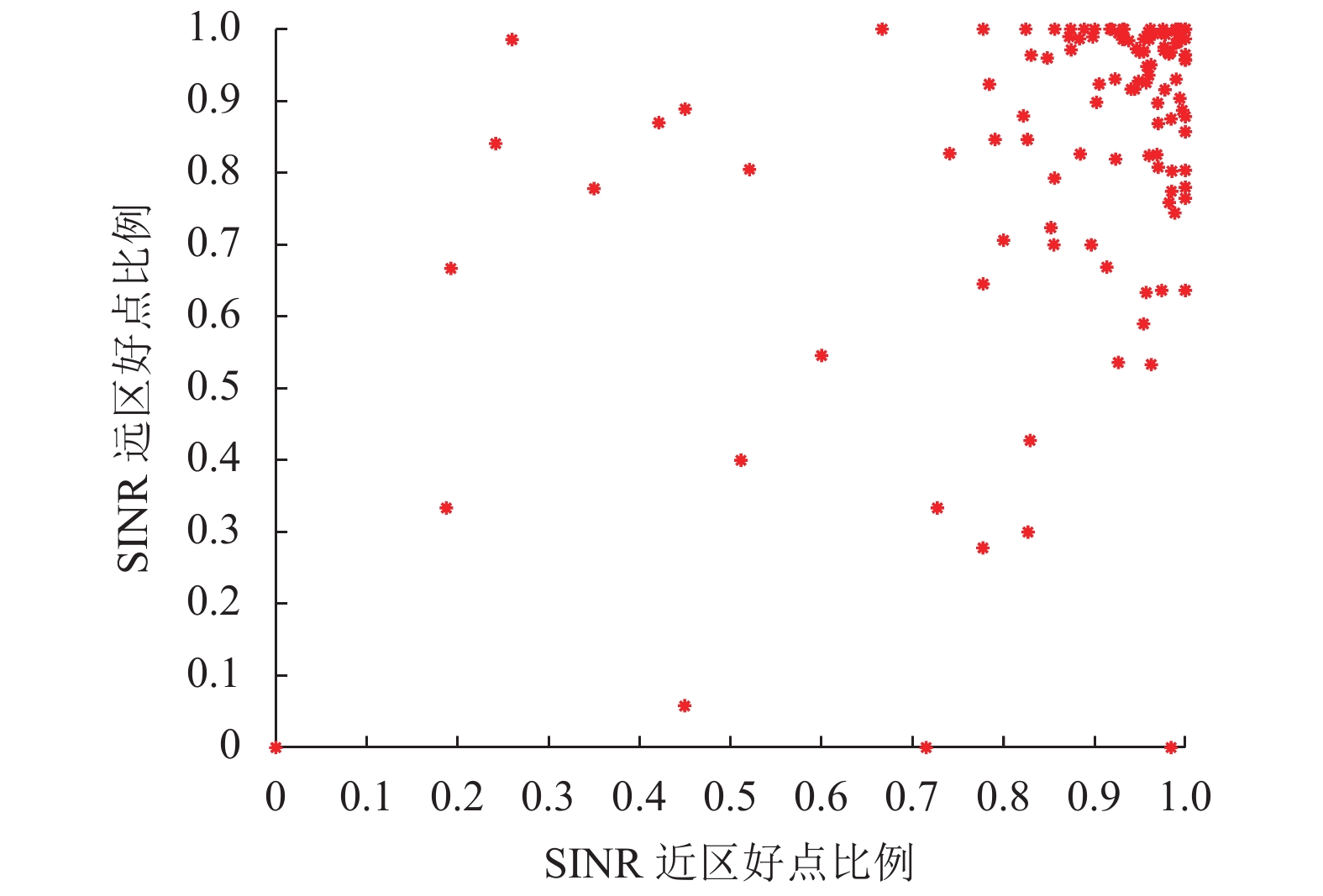
本文提出了基于距离因素的四维特征, 分别为SINR近区好点比例、SINR远区好点比例、RSRP近区好点比例和RSRP远区好点比例. SINR近区好点比例为近区SINR>3 dBm的信号点的比例; SINR远区好点比例为远区SINR>0 dBm的信号点的比例; RSRP近区好点比例为近区RSRP>–90 dBm的信号点的比例; RSRP远区好点比例为远区RSRP>–100 dBm的信号点的比例. 其中, 将距离基站最近的信号点和最远的信号点的距离的平均值作为阈值, 大于阈值的区域为远区, 小于或等于阈值的区域为近区. 为了分析特征的可分性, 更加直观的观察特征, 将RSRP近区好点比例作为x轴, RSRP远区好点比例作为y轴, 得到图4; 将SINR近区好点比例作为x轴, SINR远区好点比例作为y轴, 得到图5.
|
图 4 RSRP好点比例图 |
|
图 5 SINR好点比例图 |
从图4和图5可以看出, 数据点集中在0.7–1之间, 说明117个小区里, 覆盖率较好的小区或者干扰较弱的小区占比较高. 优良小区集中分布, 呈现较好的集聚现象. 由此可得, 特征能将优良小区和质差小区区分出来, 可以用分类器进行分类.
1.4 数据标定目前对于质差小区的检测, 很大程度上依据的是网优工作人员的经验. 传统的路测, 需要网优人员结合多个质量指标的统计数据, 利用路测分析软件对小区进行判断和评估, 存在正确率不够、效率低下等问题.
为了提高基于路测数据对质差小区检测的效率, 更为准确的判断小区的优劣情况, 采用聚类算法结合人工标注的方法进行标定. 本研究采用的聚类算法为k均值聚类(k-means clustering algorithm, k-means)算法. 该方法是最为常用的一种无监督算法. 首先随机选择k个点作为质心,k的选值需要人为设定. 再计算数据集中的每一个点离质心的欧式距离或者余弦距离等, 将其分配到距其最近的质心所在的簇. 之后每个簇的质心更新为这个簇中所有点的平均值, 直到满足终止条件. 这种算法简单快速容易实现, 能够体现数据在几何和统计学上的意义[10].
先利用k均值聚类算法, 将k值设定为2, 即将所有的小区划分为两类, 简单分析后将优良小区标注为1, 质差小区标注为0. 网优人员结合聚类结果, 在路测分析软件上进行分析, 将结果进一步细化, 得到最终分类结果. 如图6所示, 在PCI为115的小区中有近一半的信号点的RSRP值低于阈值, 因此小区覆盖下的信号强度不理想, 应为质差小区. 同时查看聚类结果, PCI为115的小区的标定值为0, 则聚类结果正确, 小区判定为质差小区. 对于判断不一致的小区, 交给另一位人员进行判断, 得到最终结果, 减少了误判率, 提高了工作的效率和判断的准确率.

|
图 6 路测软件分析图 |
2 分类器选择 2.1 选择标准
分类器根据学习的方式主要分为无监督学习分类器和有监督学习分类器. 无监督学习的分类器可以利用未标记的数据, 找到其中的隐藏结构, 根据样本之间的相似性进行分类; 监督学习的分类器依据标签, 在分类好的数据基础上判断一个新的数据所属的类别.
选择分类器时, 既要考虑分类器本身的特性, 又要考虑各式数据集在训练时带来的影响. 无线网络的LTE小区的路测数据经过数据处理、特征提取、数据标注后, 产生117×4的特征矩阵和标签, 将其输入到分类器中, 可以看出, 训练数据为一个小样本, 维度较高的数据集, 应当选择属于适用于小样本的分类器. 结合实际, 实际的网优工作, 分类器应该具有较好的可解释性, 可以在工作中, 提供较好的指导性. 考虑到实际的工程应用, 分类器的计算复杂度, 要选择快速且资源消耗小的算法.
2.2 算法概述 2.2.1 逻辑回归算法逻辑回归(logistics regression)算法是监督学习的一种常用算法, 主要解决二分类问题. 假设训练集
| ${h_\theta }(x) = \frac{1}{{1 + \exp ( - {\theta ^{\rm T}}X)}}$ | (1) |
| $J(\theta ) = \frac{1}{m}\sum\limits_{i = 1}^m {{{Cos}} t({h_\theta }({x^i}),{y^i})} $ | (2) |
| ${{Cos}} t({h_\theta }(x),y) = - \log ({h_\theta }(x)), \; {\rm if} \; y = 1$ | (3) |
| ${{Cos}} t({h_\theta }(x),y) = - \log (1{\rm{ - }}{h_\theta }(x)), \; {\rm if} \; y = 0$ | (4) |
其中,
支持向量机(Support Vector Machine, SVM)算法, 是基于统计学习理论的一种监督机器学习的方法. 支持向量机可以找到一个最优分类超平面, 这个超平面能够使其两侧的空白区域最大化, 而且不失分类的精度[11]. 它在小样本数据上能够得到较好的结果, 而且具有优秀的泛化能力. 但是运用在大数据集上会出现训练时间过长和准确率不够的问题.
2.2.3 决策树算法决策树算法属于监督学习, 可以分为分类树和回归树. 分类树可以基于不同的条件分割数据集. 首先根据信息增益或者信息增益率来寻找最优特征, 然后根据特征中的最优值将数据集分成两个子数据集, 之后重复以上操作, 直到满足终止条件. 信息增益和信息增益率的公式为:
| $G{\rm{ain}}(D,a) = Ent(D) - \sum\nolimits_{v = 1}^m {{p_v}} Ent({D^v})$ | (5) |
| $Gain\_ratio(D,a) = \frac{{Gain(D,a)}}{{ - \displaystyle\sum\nolimits_{v = 1}^m {{p_v}{\rm {Log}}_{2}{p_v}} }}$ | (6) |
其中, a是特征, v是其中的一个分类,
k最近邻(k-Nearest Neighbor, kNN)分类算法是一种广泛应用的监督学习算法.k近邻算法遇到一个未知类别的新样本时, 根据一些已知类别的样本, 可以找到k个距离最小的邻居样本. 新样本就属于类别中含有这些邻居数量最多的类. 这种算法理论基础成熟, 准确度高, 但对于大数据集来说, 计算量大, 所需内存多, 会造成运行时间过长等问题.
综上所述, 选择逻辑回归分类器、支持向量机分类器、决策树分类器和k近邻分类器这4种较为简单的算法作为质差小区的检测的算法, 并通过结果对比分析, 得到最适合的分类器.
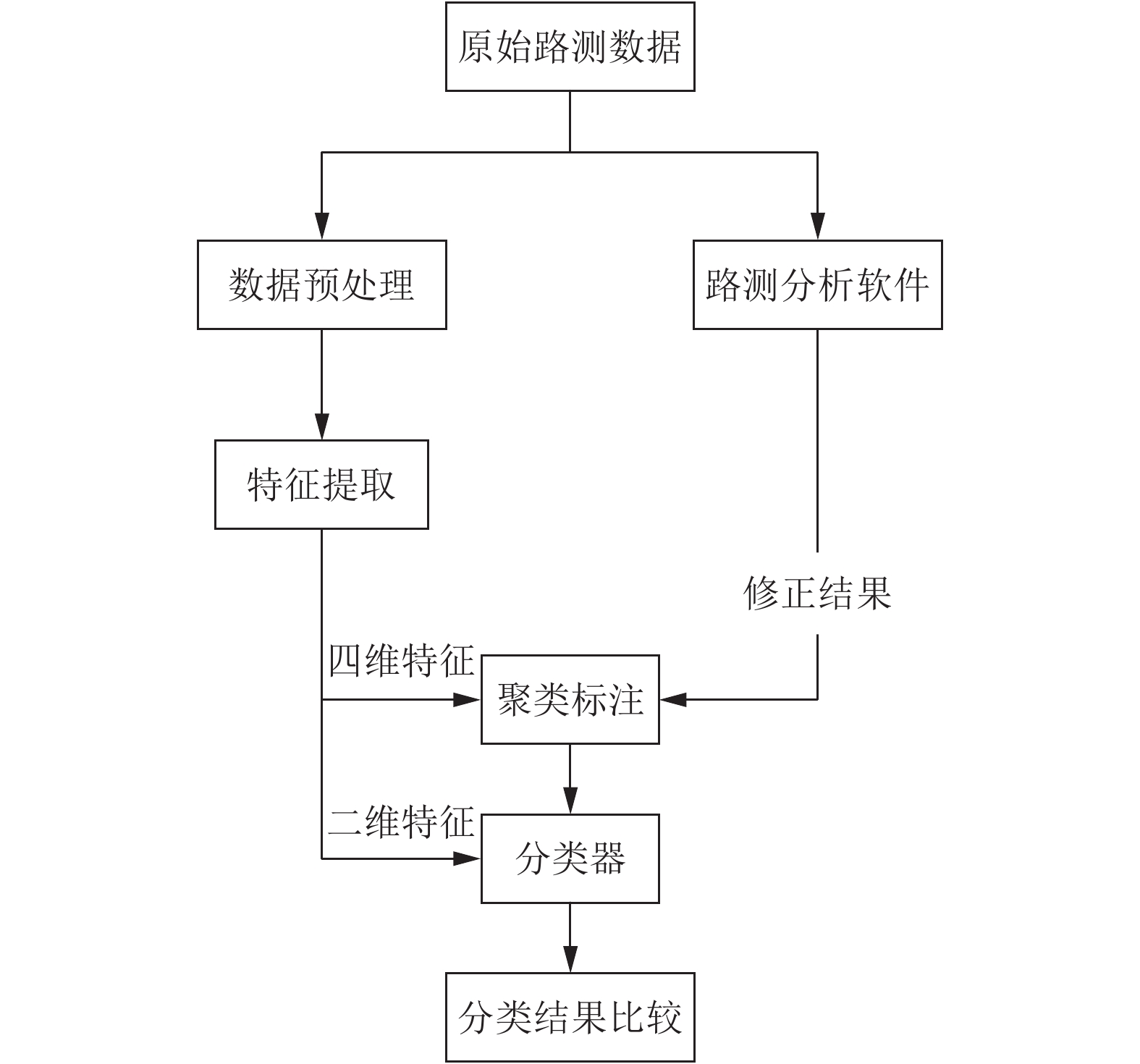
3 实验与结果分析 3.1 实验设计本文提出的基于机器学习的质差小区检测方法的整体流程图如图7所示.
|
图 7 整体流程图 |
整个过程主要分为3个部分: 特征提取、数据标注和分类结果比较. 其中特征提取可以为分类器提供训练数据基础; 数据标注将质差小区的检测问题, 转化成机器学习中分类问题; 分类器结果比较是将两维特征(即RSRP采样率和SINR采样率)与基于距离的四维特征分别输入到每一种分类器中进行分类, 将其结果进行比较; 若四维特征得到较高的分类准确率, 则将其准确率和运行时间综合比较, 最终选择出分类效果最好的分类器.
为了最小化模型结构风险, 本实验采用10折交叉验证对性能进行评估, 将数据集平均分成10份, 轮流将其中的9份做训练, 1份做验证, 并将10次结果的均值作为对算法精度的估计, 得到每种算法较为合理的准确率.
3.2 特征的比较为了验证四维特征的可行性, 分别使用逻辑回归分类器、支持向量机分类器、决策树分类器和k近邻分类器4种分类器对提取的四维特征和二维特征分别进行分类比较. 二维特征和四维特征在不同分类器下的准确率结果见表1.
| 表 1 二维特征和四维特征在不同分类器下的准确率 |
由表1可以看出, 四维特征比二维特征在每一种分类器中的分类准确率都高10%左右, 由此可得, 四维特征具有更高的分类准确率, 证明了四维特征的可行性, 说明了基于距离的四维特征在基于机器学习的质差小区的检测中具有一定的实际意义.
3.3 分类器的选择选取逻辑回归分类器、支持向量机分类器、决策树分类器和k近邻分类器4种分类器, 得到了四维特征在该4种分类器中的结果如表2所示.
| 表 2 四维特征在不同分类器下的准确率和运行时间 |
由表2可以看出, 在这4种分类器, 支持向量机分类器, 表现出了更加优异的分类性能(准确率高且运行时间短). 且四维特征在该分类器下得到的混淆矩阵和ROC曲线如图8和图9所示.
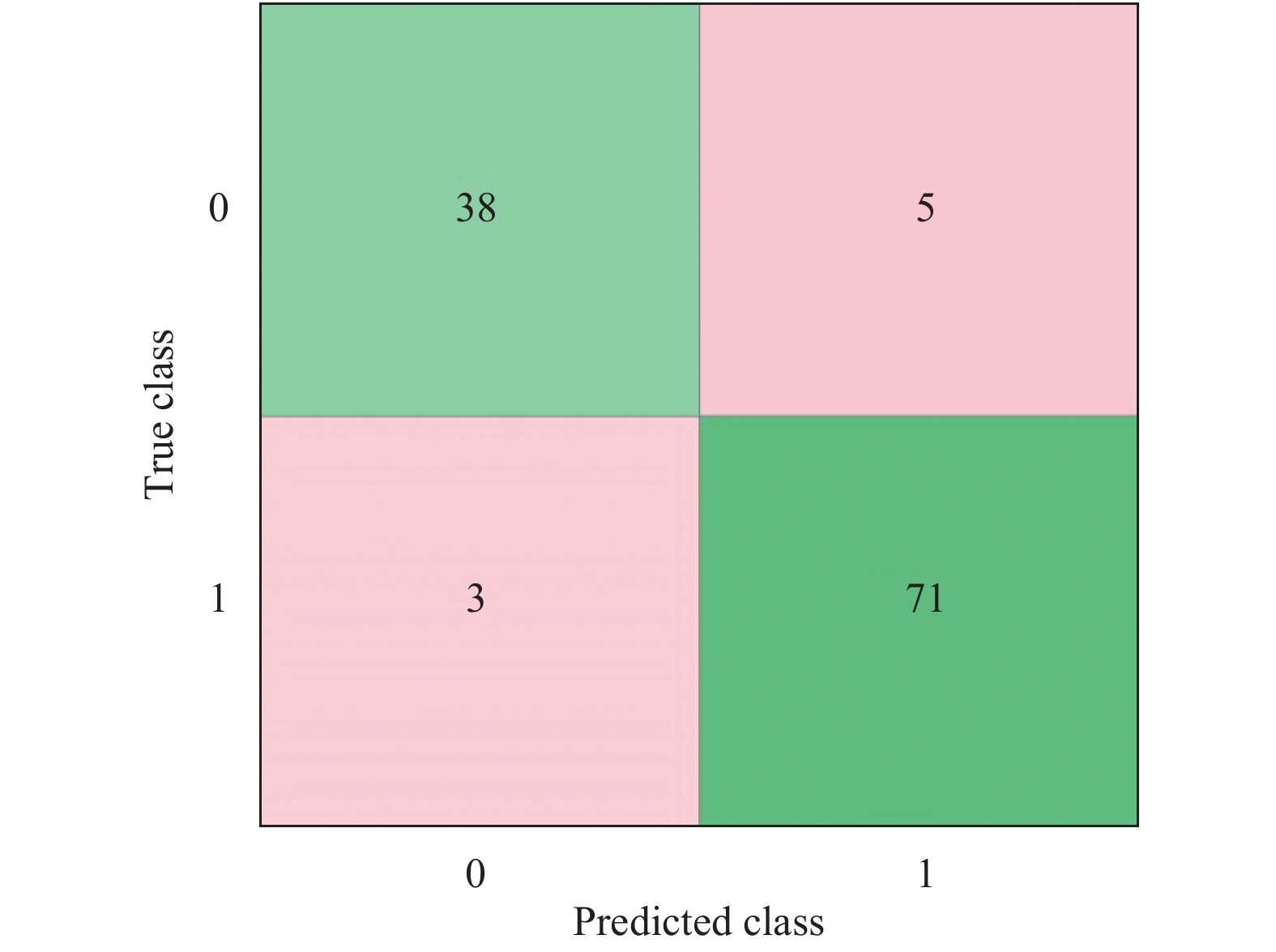
由图8可得, 人工标注质差小区为43个, 其中有38个被正确预测为质差小区, 有5个被错误的预测为优良小区; 人工标注优良小区为74个, 有71个被成功预测为优良小区, 3个被错误预测为质差小区. 可以看出, 支持向量机分类器对于四维特征的分类效果良好, 错误分类在可接受的范围内.
|
图 8 混淆矩阵 |
|
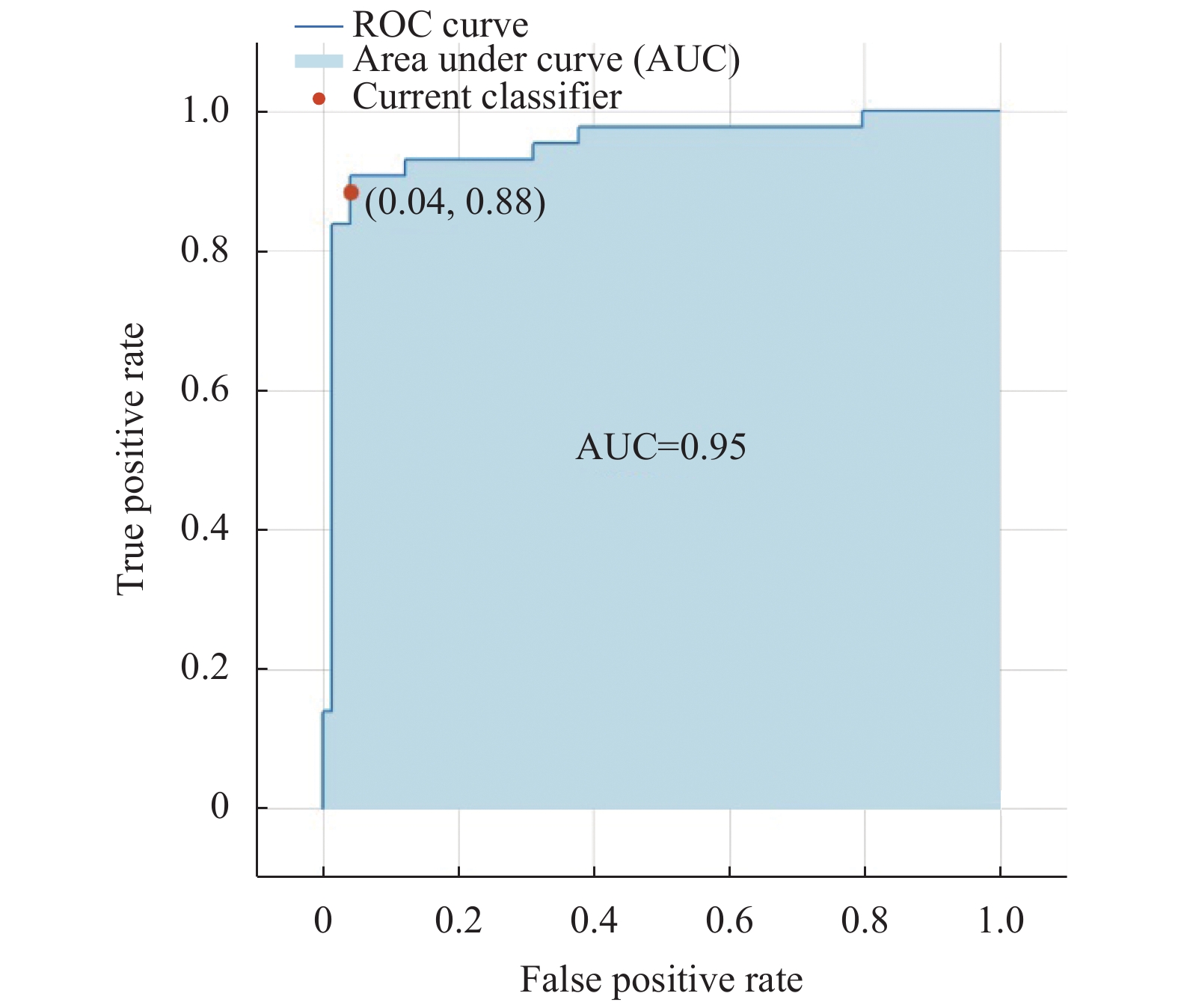
图 9 ROC曲线 |
ROC曲线的横轴代表负正类率特异度, 纵轴代表真正类率灵敏度, 通过曲线可以很容易的查到任意界限值时的分类能力.AUC为ROC曲线下的面积, 它作为数值可以直观的评判分类器的好坏, 取值在0.1到1之间, 由图9可以看出, 支持向量机分类器的AUC为0.95, 说明支持向量机分类器性能比较好.
通过实验可以发现, 对于常用的4种分类器, 本文提出的基于距离的四维特征相比传统的两维特征均获得了更高的准确率, 说明了将距离因素引入质差小区的检测能得到更加准确的分类结果, 其中在支持向量机中得到了最好的结果.
4 结论本研究将距离因素引入到传统的路测数据中, 得到了基于距离的四维特征. 分析比较了二维特征与四维特征在逻辑回归分类器、支持向量机分类器、决策树分类器和k近邻4种分类器中的效果, 并分析了四维特征在4种分类器中的分类准确率和运行时间. 根据以上研究可以得出:
(1)使用四维特征与二维特征进行机器学习的分类检测比较, 四维特征能够获得较好的区分结果.
(2)对比逻辑回归分类器、支持向量机分类器、决策树分类器和k近邻分类器4种分类器, 在二维特征和四维特征中, 支持向量机分类器均获得了最好的分类效果.
所以, 将距离因素引入到对路测数据进行质差小区检测能够得到更好的结果, 解决了单一指标在质差小区检测中准确度不够的问题, 在路测数据中为机器学习在质差小区检测中的应用提供了理论依据, 具有一定的现实意义.
| [1] |
果敢, 于力, 魏然. 无线网络优化的路测. 电信技术, 2005(1): 20-22. DOI:10.3969/j.issn.1000-1247.2005.01.007 |
| [2] |
王西点, 王磊, 龙泉, 等. 人工智能及其在网络优化运维中的应用. 电信工程技术与标准化, 2018, 31(7): 81-86. DOI:10.3969/j.issn.1008-5599.2018.07.019 |
| [3] |
张喆. 基于K-means的LTE宏站小区场景聚类策略. 通信技术, 2019, 52(3): 668-673. DOI:10.3969/j.issn.1002-0802.2019.03.026 |
| [4] |
Kibria MG, Nguyen K, Villardi GP, et al. Big data analytics, machine learning, and artificial intelligence in next-generation wireless networks. IEEE Access, 2018, 6: 32328-32338. DOI:10.1109/access.2018.2837692 |
| [5] |
周鹏. 数据挖掘在通信网络优化中的应用研究[硕士学位论文]. 南京: 南京邮电大学, 2017.
|
| [6] |
曾雨桐. 数据挖掘算法在网络优化话务量和差小区挖掘中的应用[硕士学位论文]. 南京: 南京邮电大学, 2016.
|
| [7] |
王希. 基于概率神经网络(PNN)的LTE质差小区分析方法. 数字通信世界, 2017(2): 89-90, 80. DOI:10.3969/J.ISSN.1672-7274.2017.02.029 |
| [8] |
林世明, 高志斌, 高凤连, 等. 基于路测的TD-LTE网络优化分析. 现代电子技术, 2015, 38(9): 12-15. DOI:10.3969/j.issn.1004-373X.2015.09.003 |
| [9] |
龙青良, 张磊. 基于用户感知的LTE网络优化关键问题研究. 邮电设计技术, 2014(10): 14-20. DOI:10.3969/j.issn.1007-3043.2014.10.004 |
| [10] |
贺玲, 吴玲达, 蔡益朝. 数据挖掘中的聚类算法综述. 计算机应用研究, 2007, 24(1): 10-13. DOI:10.3969/j.issn.1001-3695.2007.01.003 |
| [11] |
丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述. 电子科技大学学报, 2011, 40(1): 1-10. DOI:10.3969/j.issn.1001-0548.2011.01.001 |
 2020, Vol. 29
2020, Vol. 29



