2. 中南大学 湘雅二医院, 长沙 410008;
3. 陆军勤务学院 战争经济实验室, 重庆 404000
2. The Second Xiangya Hospital, Central South University, Changsha 410008, China;
3. Laboratory of War Economy, PLA Army Logistics University, Chongqing 404000, China
虚拟现实(Virtual Reality, VR)技术在近年来结合各个行业有了跨越式的发展[1], 在医学培训领域中应用也十分广泛, 特别是利用VR技术开发的虚拟手术系统(Virtual Surgery, VS). 虚拟手术系统以其操作可重复性、逼真的沉浸感而广受医疗培训人员的欢迎[2]. 在虚拟手术系统中, 流血模拟是其重要组成部分, 其伴随着手术过程频繁出现, 是虚拟手术系统逼真性和完整性的重要体现. 为了确保流血模拟的真实性, 需要解决流血过程中与软组织的碰撞检测.
碰撞检测的对象大致可以分为刚体、软体和流体. 层次包围盒[3]作为一类经典的碰撞检测算法, 大量应用于处理刚体间的碰撞检测, 如游戏设计、计算机辅助设计等领域. 构成层次包围盒树的包围盒类型有很多种, 其中较为著名的有轴向包围盒[4], 方向包围盒[5], 包围球, 离散有向多面体包围盒[6], 凸包包围盒等[7].
近年来, 国内外研究者对刚体与软体以及软体间的碰撞检测做了大量的研究, Wang TT等[8]实现了一种可形变四面体之间的连续碰撞检测, 该算法能处理软体间精确连续碰撞检测的同时, 鲁棒性和实时性都很好. 但由于流体不同于软体, 其拓扑结构变化较大, 更新结构的代价也较大, 不能简单的使用上述算法. 在流体与刚体或软体碰撞检测方面, Vanhoey等[9]提出一种欧拉网格流体与弹簧振子刚体模型之间的碰撞检测, 但其刚体模型不能太精细, 否则实时性受到很大的影响. Chentanez等[10]提出一种SPH流体粒子与有限元四面体网格之间的碰撞检测算法, 通过在血管壁上附着SPH粒子并对其进行约束从而实现血管与血管壁碰撞检测的效果, 该算法能处理SPH流体与有限元刚体或软体之间的碰撞检测, 但对软体的动力学模型有相应的要求, 适应性不强, 特别是对虚拟手术中流血与软组织器官的碰撞检测, 限制了软组织器官动力学模型的选择范围. 宗智等[11]将SPH模拟的流体粒子与质点弹簧模型(Mass-Spring Model, MSM)之间进行碰撞检测, 实现了血液流动与血管壁形变之间的相互作用, 从而模拟出了血液在血管里面流动的现象. 但必须使用MSM模型作为软件组织的动力学模型的限制, 使其无法在流体与软体间的碰撞检测中广泛推广.
本文针对流体与软体碰撞检测的问题, 提出一种基于空间划分的SPH流体粒子与软体碰撞检测算法, 该算法首先对虚拟手术系统中流血粒子与软组织器官碰撞检测的特点进行分析, 在此基础上进行SPH流体粒子与软体组织表面的碰撞检测研究. 该算法克服了以往研究中对软体组织模型选择的局限性, 而且实现了精确性和实时性上的优化, 以满足虚拟手术流血模型对碰撞检测要求.
1 虚拟手术流血碰撞检测的特点在虚拟手术系统中, 流血模拟是关系着整个系统真实性和沉浸感非常重要的一环, 而处理流血与器官或者皮肤表面的碰撞检测是流血模型中必不可少的部分. 本文采用SPH算法作为流血模拟的流体动力学模型. SPH算法是一种对流体力学方程—Navier-Stokes方程进行离散化求解的拉格朗日粒子法. 在本文中, 主要关注SPH流血粒子与虚拟软组织器官表面三角面片之间的碰撞检测. 这类碰撞有以下几个特点:
1) 流血粒子的相邻关系和空间位置在每一个时间步内变化都很大, 要求进行碰撞检测的结构更新算法能快速适应和处理流体的拓扑结构变化, 这就决定了很难采用层次包围盒树对拓扑结构进行更新.
2) 虚拟器官软组织不同于刚体, 其形态和相对位置会随着形变和切割而改变, 这就要求碰撞检测算法能够处理和感知到这种变化.
3) 流血粒子与虚拟器官软组织之间的碰撞检测对精确性也需要相当的保证, 否则流血粒子很有可能穿透到虚拟器官软组织内部, 模拟效果也大打折扣.
2 算法概述在处理大规模三维场景下的碰撞检测时, 不同碰撞检测算法的共同特点是进行逐层次、由粗到细的碰撞检测, 即先将明显不可能相交的空间进行快速排除, 再对已缩小范围中的物体进行更为精确的判断. 本文提出的碰撞检测算法能结合SPH算法中最近相邻粒子搜索(Nearest Neighboring Particle Search, NNPS)过程进行碰撞检测空间的均匀划分, 并通过均匀划分的空间快速确定碰撞检测范围, 在保证空间划分时间和三角面片定位时间适当的同时, 尽可能的减少精确的基元间碰撞检测的次数.
2.1 基于空间划分的碰撞检测算法基于空间划分的碰撞检测算法是一种确定粗略碰撞检测范围的算法: 将空间划分为不同区域并测试基元是否在同一空间区域中相交. 这种方法大大降低了基元测试的数量[12]. 对于三维空间中可形变物体的碰撞检测, 一般采用均匀网格对空间实施覆盖, 其优势在于确定任意点所在的均匀网格单元序号十分简单: 只需利用世界坐标系的值除以网格单元长度即可. 一般可将基于空间划分的碰撞检测算法分为3个阶段, 首先确定碰撞检测空间范围并在该空间上划分空间网格单元, 再根据划分好的网格单元确定需测试基元所在的网格序号, 最后遍历所有网格单元, 对网格单元中包含两种以上基元的网格进行基元间的精确碰撞检测.
2.2 基于空间划分的SPH流体粒子与虚拟器官软组织碰撞检测算法本文提出的碰撞检测算法对传统的空间划分碰撞检测算法进行改进的地方是: 利用SPH算法NNPS过程中划分的均匀网格空间对流体粒子和软组织三角面片进行定位. 相对于传统的基于空间划分的碰撞检测算法, 本算法节省下了进行空间划分以及SPH流血粒子定位的资源消耗, 很大程度上的降低了算法的时间复杂度[13].
在本节中, 首先介绍SPH算法进行流血模拟的过程, 并针对SPH算法进行邻域搜索时间复杂度过高的问题, 提出基于均匀空间划分的NNPS过程, 再结合NNPS过程进行SPH粒子和器官表面三角面片的定位, 然后进行基元间的碰撞检测计算.
2.2.1 基于SPH算法的模拟流体对于模拟流体效果的流体模拟来说, 主要是求解不可压缩流的Navier-Stokes方程, 其形式如下:
| $\dfrac{{\partial \vec u}}{{\partial \vec t}} + \vec u.\nabla \vec u + \dfrac{1}{\rho }\nabla p = \vec g + \nu {\nabla ^2}\vec u$ | (1) |
| $\nabla \vec u = 0$ | (2) |
在上述公式中,
| ${A_s}(r) = \sum\limits_j {{m_j}} \frac{{{A_j}}}{{{\rho _j}}}W(r - {r_j},h)$ | (3) |
其中, j表示的是r的邻域中粒子的序号, mj表示的第j个粒子的质量, rj是粒子j的位置坐标,
SPH算法中, NNPS过程对算法的实时性影响较大, 若采用遍历搜索法, 则其时间复杂度为O(n2), n为粒子数目, 显然会成为SPH算法的瓶颈. 基于空间划分的方法进行NNPS过程能将NNPS过程的时间复杂度降低到O(nm), 其中, m表示单元三维网格内流血粒子的平均数目, 显然, 采用基于空间划分的方法进行NNPS过程能大大降低其计算资源的消耗.
在基于空间划分的NNPS过程中, 首先根据流体的范围确定三维坐标的最大值(xmax, ymax, zmax)和最小值(xmin, ymin,zmin), 根据最大值和最小值划定的范围, 以光滑长度h对空间进行垂直坐标系3个方向上的划分, 划分后, 流体运动的空间就被包含在三维网格中, 并伴随着流体的运动不断改变, 如图1所示.
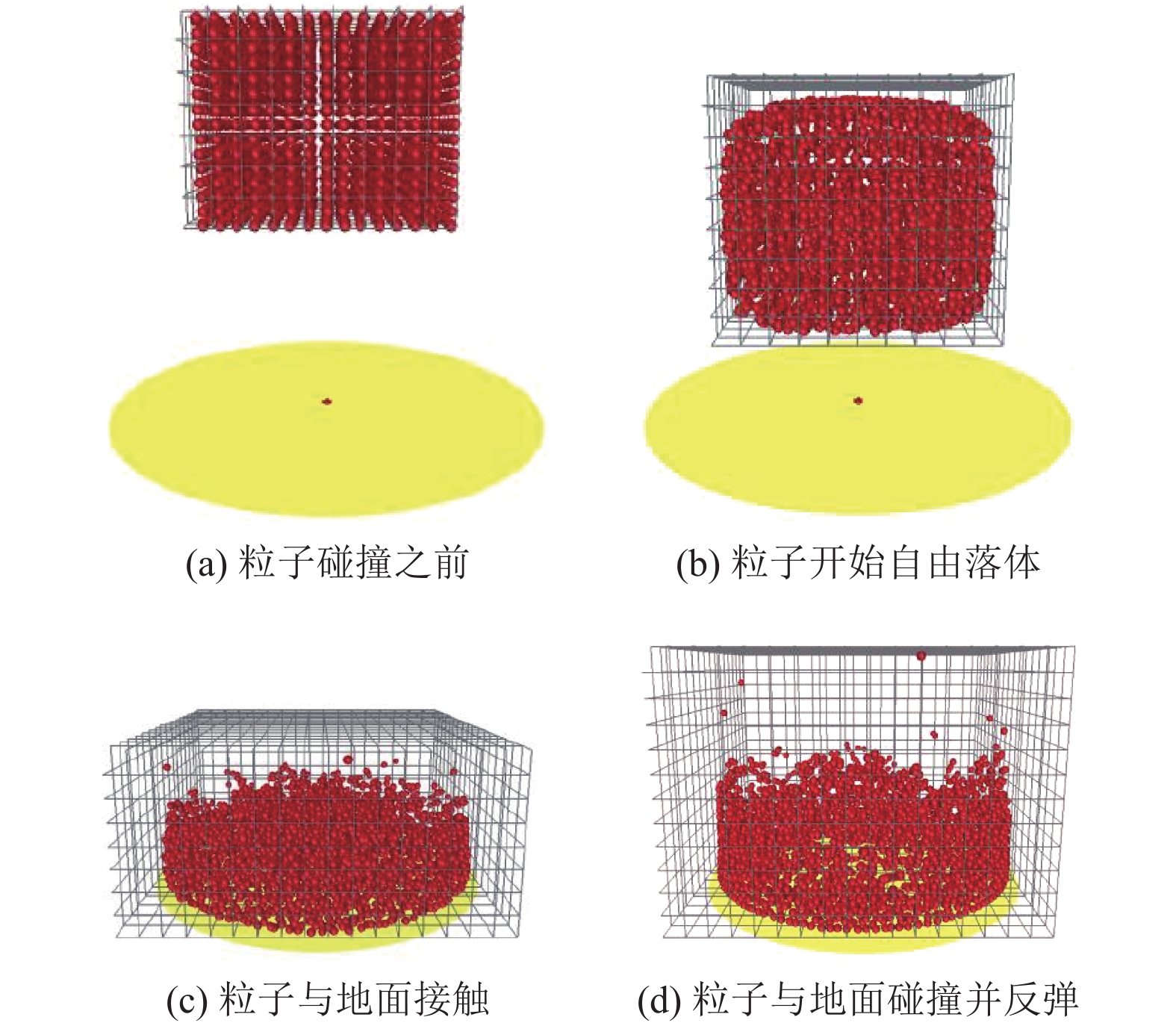
|
图 1 SPH算法中NNPS过程划分的网格空间 |
基于空间划分的NNPS过程建立的三维均匀空间网格可以复用于本文算法中碰撞检测范围确定以及SPH流血粒子的定位.
2.2.3 空间网格长度划分依据以及对碰撞检测算法精度和性能的影响光滑长度的确定决定了粒子的影响范围, 光滑长度过长, 则影响范围中的粒子过多, 计算复杂度增加; 光滑长度过短, 则影响范围内粒子太少, 不能表现出粒子的性质; 所以选择一个合适的光滑长度对SPH算法以及碰撞检测算法都非常重要.
由于本算法着重于表达流体效果, 而非精确的物理仿真, 对流体的计算不需要非常精准, 所以我们认为处理的流体密度在任何时候都是均匀的. 基于以上设定, 我们可以选择固定的光滑长度h, 其数值与流体的密度成反比[14].
用于碰撞检测的空间网格使用的是NNPS过程中建立起来的空间网格. 在光滑长度h是常量的情况下, 我们采用h作为NNPS网格划分的单元长度, 这样, 对于给定空间中的粒子, 其相邻粒子只能在本身所在的网格或者相邻的网格中. 在一维、二维、三维空间中, 寻找相邻粒子只需要搜索对应的3、9、27个单元即可.
在本文提出的碰撞检测算法中, 空间网格的大小对算法性能的影响较大, 单元网格尺寸太大会导致过多流血粒子和三角形包围到同一网格中, 从而增加了基元测试的负担, 太小又会导致一个三角形占用过多网格, 并影响碰撞检测的精确性. Ericson等的研究表明, 当三维网格大小与三角形的AABB包围盒尺寸相当时为最优[15], 因此我们取所有三角形的AABB包围盒尺寸的平均值.
鉴于上述两种方案都需要影响空间网格的尺寸和数量, 所以我们将两者计算出来的网格长度取平均值, 使得网格长度兼顾流体模拟和碰撞检测.
空间网格的数量由流体所分布的空间所决定的, 我们使用计算出来的网格长度对空间进行分割. 比较典型的例子如图1(b)所示, 网格数量为
本文提出的算法能将SPH算法中基于空间划分的NNPS过程用于空间均匀划分并将流体粒子定位. 要进行基于空间划分的碰撞检测, 还需利用划分出来的均匀空间网格进行软组织表面三角面片的定位. 对于软组织表面的三角面片i的顶点(xi, yi, zi), 用其减去SPH算法中NNPS过程确定的最小坐标值(xmin, ymin, zmin), 再除以单元网格的长度h, 得到网格序号
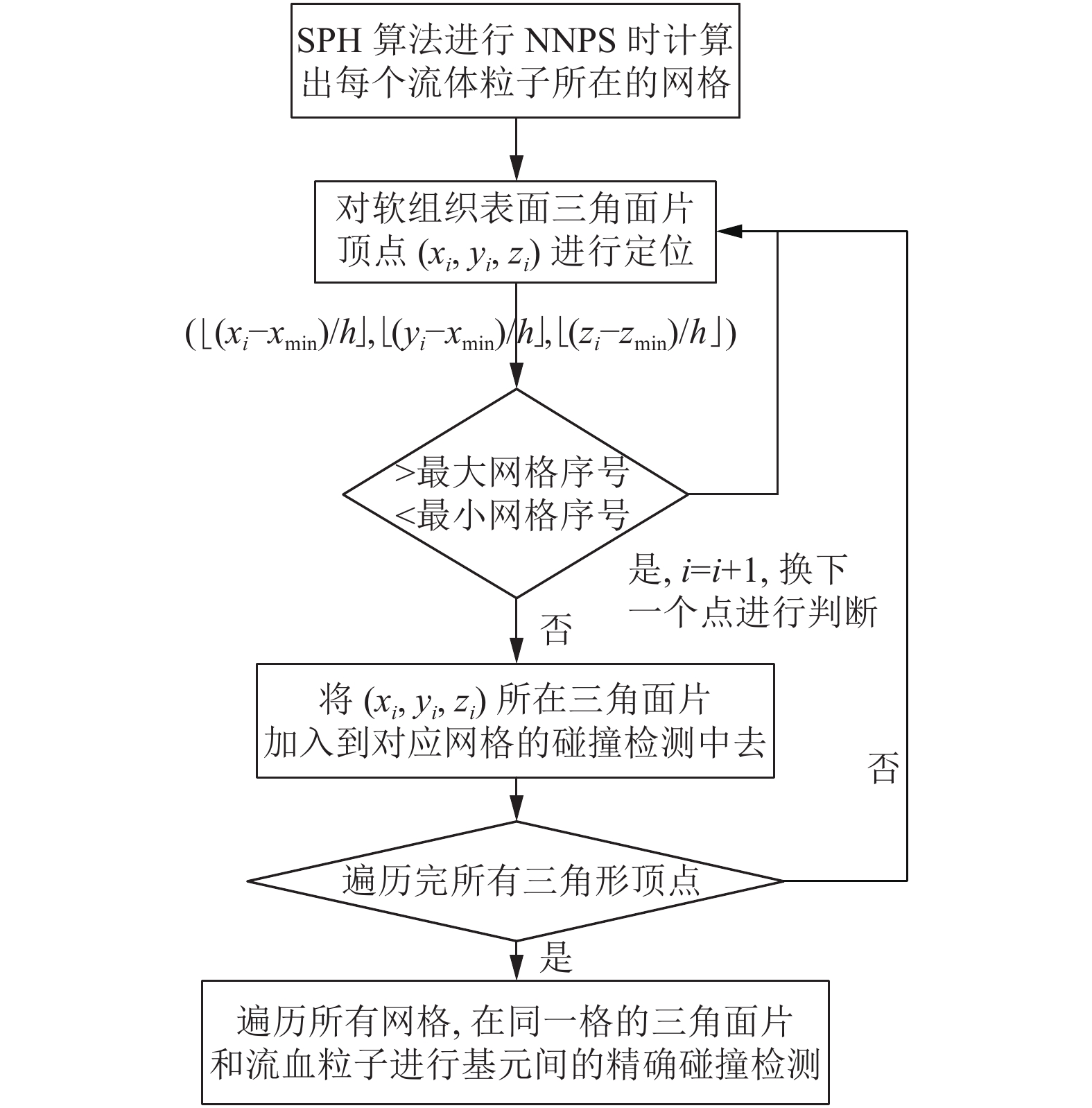
|
图 2 碰撞检测算法流程 |
3 实验结果及分析
对本文提出的基于空间划分的碰撞检测算法进行实验, 试验环境为Interi7 9500 K CPU, 16 GB内存, NVIDIA GeForce GTX1080显卡. 使用VS 2017, OpenGL编程实现算法. 实验的对比算法是传统的基于空间划分的碰撞检测算法. 本文的算法中, 由于空间划分过程和流血粒子定位过程均在基于SPH算法的流体模拟过程实现, 其相对于传统的空间划分算法优势明显, 结果如图3、图4所示, 图3是传统的空间划分算法的时间性能表现, 图4是本文所提出的算法的时间性能表现. 时间性能对比如表1和表2所示.
对肝脏软组织与流血粒子的碰撞检测进行实验, 肝脏表面三角面片数量为13 070, 粒子数目为4800, 模拟的帧率为151 fps, 模拟效果如图3所示.
对流血粒子使用Marching Cubes算法进行表面渲染, 模拟肝脏表面流血的效果, 结果如图4所示.
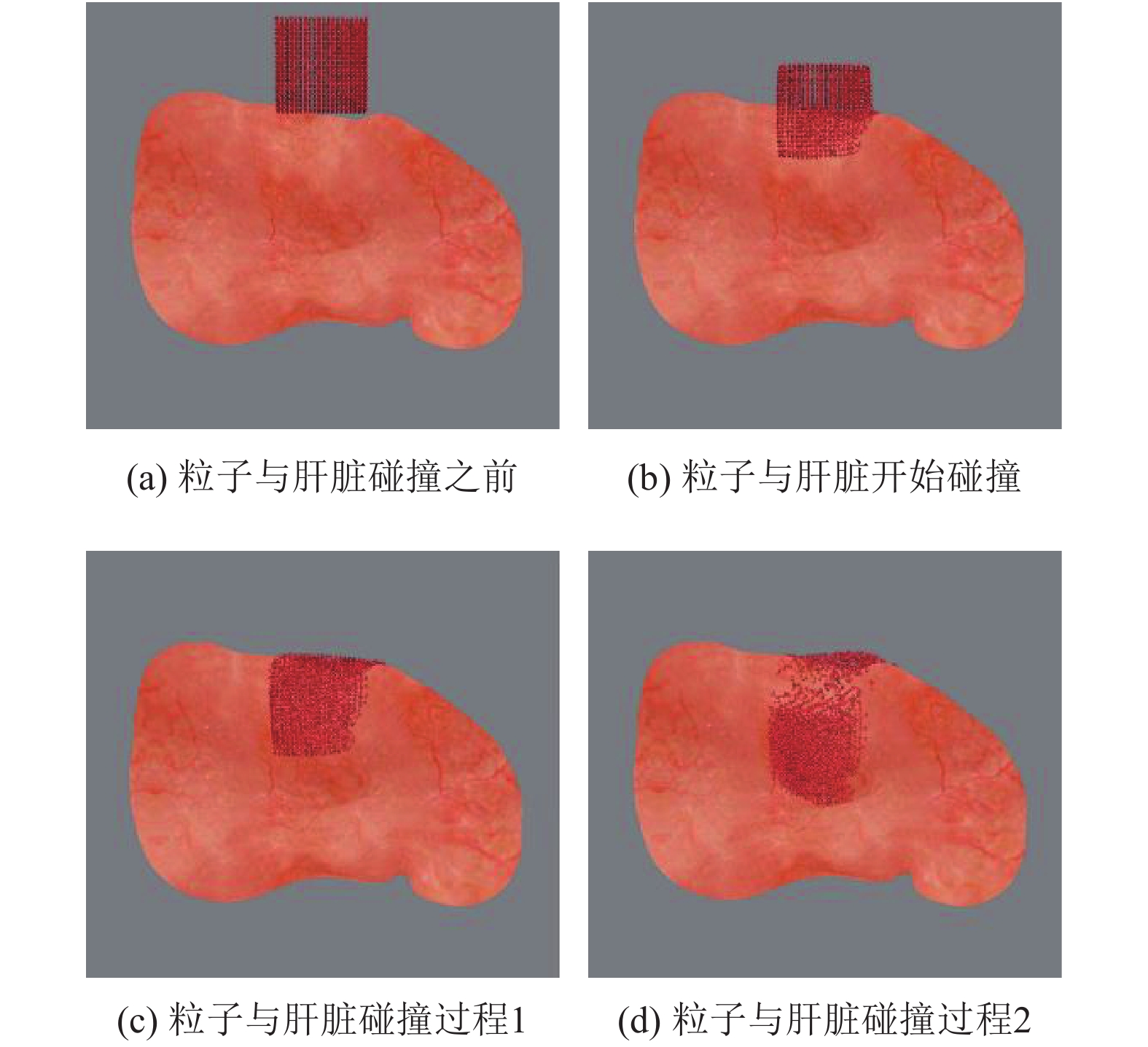
|
图 3 流血粒子与肝脏表面碰撞检测模拟 |

|
图 4 模拟肝脏表面流血效果 |
| 表 1 传统算法时间性能(单位: ms) |
| 表 2 本文算法时间性能(单位: ms) |
将本文算法运用到虚拟肝脏手术中, 虚拟肝脏实质切开后, 肝脏产生形变, 伤口内部开始渗血, 流血能够根据虚拟肝脏形态的变化进行自适应的调整, 具体结果见图5.
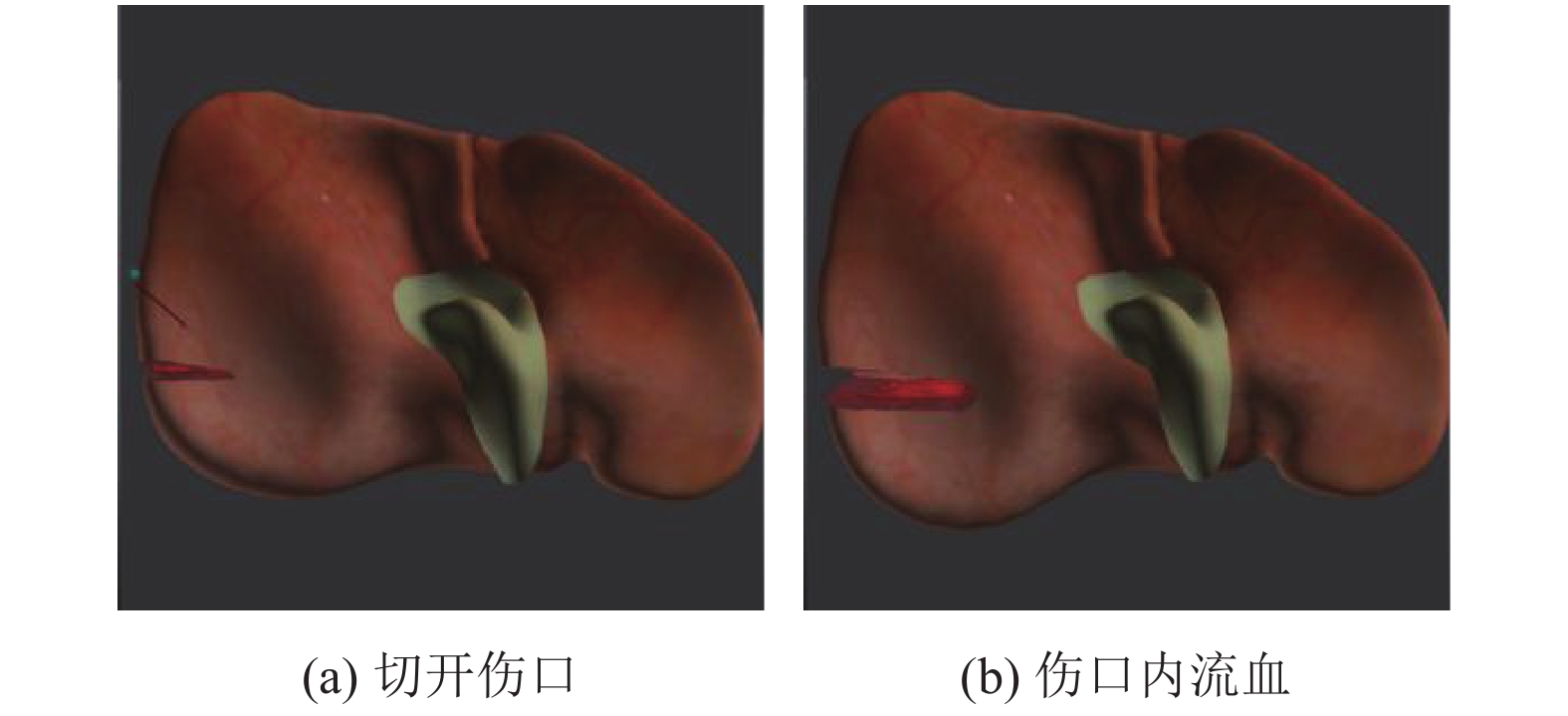
|
图 5 使用本文算法模拟虚拟肝脏手术流血 |
4 结束语
虚拟手术中的流血模拟对碰撞检测的实时性和精确性均有较高要求, 由于手术仿真的过程中涉及到软体模型的形变和切割, 给流血模拟的碰撞检测带来很大的难度. 本文论述了虚拟手术流血模拟中碰撞检测问题的特点, 并给出了一种基于空间划分的SPH流体粒子与软碰撞检测算法. 该算法不仅能有效提高碰撞检测实时性, 而且能实现SPH模拟的流体粒子与任意动力学模型的软体模型之间的精确碰撞检测. 下一步, 将此算法结合GPU加速, 使算法实时性进一步提高. 实验证明, 该方法能满足虚拟手术流血模拟的要求.
| [1] |
周思跃, 龚振邦. 虚拟现实定义的探讨. 计算机仿真, 2006, 23(9): 219-222. DOI:10.3969/j.issn.1006-9348.2006.09.057 |
| [2] |
潘伟洲, 赵仕豪, 徐泽坤, 等. 沉浸式手术环境的研究与实现. 计算机仿真, 2013, 30(12): 411-415. DOI:10.3969/j.issn.1006-9348.2013.12.095 |
| [3] |
史旭升, 乔立红, 朱作为. 基于改进OBB包围盒的碰撞检测算法. 湖南大学学报(自然科学版), 2014, 41(5): 26-31. |
| [4] |
张闻雷, 王健熙, 罗小川, 等. 基于包围盒十字相交的装配干涉检测方法. 计算机集成制造系统, 2015, 21(7): 1725-1733. |
| [5] |
施鹏, 熊岳山, 徐凯, 等. 虚拟肝脏手术中实时动态渗血效果模拟. 计算机应用, 2013, 33(10): 2911-2913, 2917. |
| [6] |
张应中, 范超, 罗晓芳. 凸多面体连续碰撞检测的运动轨迹分离轴算法. 计算机辅助设计与图形学学报, 2013, 25(1): 7-14. DOI:10.3969/j.issn.1003-9775.2013.01.002 |
| [7] |
唐磊, 施侃乐, 雍俊海, 等. 模型适应的凸包围多面体并行生成算法. 中国科学: 信息科学, 2014, 44(12): 1515-1526. |
| [8] |
Wang TT, Liu ZH, Tang M, et al. Efficient and reliable self-collision culling using unprojected normal cones. Computer Graphics Forum, 2017, 36(8): 487-498. DOI:10.1111/cgf.13095 |
| [9] |
Vanhoey K, Sauvage B, Génevaux O, et al. Robust fitting on poorly sampled data for surface light field rendering and image relighting. Computer Graphics Forum, 2013, 32(6): 101-112. DOI:10.1111/cgf.12073 |
| [10] |
Chentanez N, Müller M, Macklin M. Real-time simulation of large elasto-plastic deformation with shape matching. Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Zurich, Switzerland. 2016. 159–167.
|
| [11] |
宗智, 邹丽, 刘谋斌, 等. 模拟二维水下爆炸问题的光滑粒子(SPH)方法. 水动力学研究与进展, 2007, 22(1): 61-67. |
| [12] |
Gregory A, Lin MC, Gottschalk S, et al. A framework for fast and accurate collision detection for haptic interaction. Proceedings of the IEEE Virtual Reality. Houston, TX, USA. 1999. 38–45.
|
| [13] |
施鹏. 虚拟肝脏手术中三维表面流血效果模拟[硕士学位论文]. 长沙: 国防科学技术大学, 2013.
|
| [14] |
步红兰. SPH方法的近斯发展与应用[硕士学位论文]. 合肥: 中国科学技术大学, 2007.
|
| [15] |
Ericson C. Real-time Collision Detection. Boca Raton: CRC Press, 2004. 145–147.
|
 2020, Vol. 29
2020, Vol. 29


