制造业对于一个国家或地区的经济发展起到关键作用, 同时也反映出国家或地区的综合实力. 2008年全球金融危机爆发后, 世界各国经济增长乏力, 各发达国家纷纷将自身传统制造业向智能制造业靠拢, 其中, 以美国与德国为首的智能制造企业发展最为迅猛. 美国于2012年提出《先进制造业国家战略计划》, 正式将先进制造业提升为国家战略, 并提出建设智能制造技术平台来加快智能制造技术创新[1]. 2013年, 德国发布“工业4.0”战略方针[2], 将智能制造作为企业发展主体. 随着信息技术和产业革命在工业领域的推进, 各种信息技术在工业领域广泛渗透, 为加快从制造大国向制造强国的转变, 我国于2015年8月提出《中国制造2025》. 随着《中国制造2025》的发布和实施, 国内的制造业纷纷走向智能化. 一些大型制造业的供应链发生巨大变革, 企业跟供应商之间由以前单纯“买卖关系”转变为“合作伙伴关系”. 随着企业与供应商关系的转变, 企业对供应商的要求越来越高. 其中, 供应商效率是制造企业对效率型供应商资源投入和价值产出的合理性考察, 它的好坏能反映供应商的优劣, 通过对供应商效率进行等级划分, 一方面可作为监督供应商的状态提供信息来源, 同时也是选择供应商激励策略的决策依据, 并实现其价值最大化. 供应商效率评价是针对效率型供应商, 通过建立合适的评价指标体系, 对这类供应商的产品质量、成本、服务等进行衡量, 并运用一定的评价标准对供应商进行效率等级划分. 供应商效率评价是构筑供应链的关键一步, 对于效率型供应链的平稳运行有很大的影响. 如何构建合适的智能制造企业供应商效率评价指标体系, 采取合适的方法对我国智能制造企业效率型供应商进行系统、科学的评价, 以及效率评价等级, 并为其提供适当的合作方案和激励策略, 是本文重点关注的研究问题.
供应商效率评价方法经历了一个从定性到定量然后到定性定量相结合的过程. 常见的定性方法有: 直观判断法、考核法、招标法和协商法等. 定性方法主观随意性太大, 结果不是很准确, 现在很少采用. 常见的定量分析法有: 层次分析法(AHP)[3]、主成分分析法(PCA)[4]、加权评分法[5]、ABC成本法[6]和因子分析法[7]等. 定量方法可以在一定程度上降低主观随意性, 但是有的个别属性判断模糊, 人为干扰因素较多, 目前单一使用这些定量方法进行研究的不是很多. 定性与定量结合的是目前供应商选择评价利用较多的方法, 常见的有模糊综合评价[8]、灰色关联理论[9]和神经网络等方法, 其中主要凸显在神经网络的研究. BP神经网络处理信息能力强、具备非线性的映射能力、容错能力、自身具有学习、联想和记忆的能力, 避免传统方法的局限性和主观随意性[10]. 关于使用BP神经网络来进行供应商评价的研究有很多, 但大多都缺乏具体的数据支撑, 存在一定的主观性. 同时, 很多利用BP神经网络的案例中, 并没有考虑构建的评价指标体系是否真正有效, 缺乏对企业的深入研究, 通用性较强而针对性较弱.
本文针对智能制造企业供应商效率评价的研究, 从智能制造视角构建智能制造企业供应商效率评价指标体系, 采用AHP-熵值法计算各指标权重, 利用信息化系统数据, 基于BP神经网络提出数据驱动下的智能制造企业供应商效率评价模型, 最后应用于国内某智能制造企业供应商效率评价研究中.
1 基础理论和方法介绍 1.1 供应商分类供应商绩效表现和战略潜力的不同, 其体现的价值也不同, 根据价值的不同提出供应商合作模式模型, 即TrueSRM[11]. 本文借鉴TrueSRM模型相关理论, 以绩效表现和战略潜力对供应商进行分类, 具体如图1所示.

|
图 1 供应商分类 |
战略型供应商(Strategic Supplier, SS)是对企业有战略指导意义的供应商, 拥有为企业创造竞争优势的核心资源, 这类供应商的数量非常少, 有的企业甚至没有. 效率型供应商(Efficient Supplier, ES)也称为普通型供应商, 是为企业提供产品最多、合作最频繁、数量最多的一类供应商, 其不掌握企业核心资源, 但企业若掌握一套方法来维护此类供应商, 可以帮助企业取得可观的价值. ES分一~五级. 问题型供应商(Problem Supplier, PS)是各类表现无法达到企业要求的一类供应商, 主要包括3类: 考察型供应商(Inspection Supplier, IS)、消极淘汰型供应商(Passive Elimination Supplier, PES)和积极淘汰型供应商(Actively Eliminate Suppliers, AES). IS一般是第一次给企业提供产品或服务, 后期的合作需要二次考察. PES是在合作期间, 为企业提供的产品、服务都未达到企业要求, 企业会在合作完成后对其进行直接淘汰. AES是合作期间, 企业想立马终止合作的一类供应商.
ES对于企业的发展起到重要的作用, 且在企业中占比最高, 本文针对ES进行深入研究.
1.2 指标权重计算AHP计算的权重结果趋向于主观, 熵值法计算结果趋向于客观, 结合两者, 采用主客观结合的方式计算指标权重, 结果更具有说服力.
(1) AHP计算指标权重
AHP是一种主观的权重计算法, 计算步骤如图2所示.

|
图 2 AHP计算步骤 |
图2中,
| $C.I. = \frac{{{\lambda _{\max }} - n}}{{n - 1}}$ | (1) |
| $C.R. = \frac{{C.I.}}{{R.I.}}$ | (2) |
其中,
| 表 1 R.I.的取值规则 |
(2)熵值法计算指标权重
熵值法是一种典型的客观赋权法[12]. 它通过计算指标体系中各指标的信息熵值, 根据指标的相对变化程度对系统整体的影响来决定指标的权重, 相对变化大的权重值大, 反之则小. 熵值法计算步骤如图3所示.

|
图 3 熵值法计算步骤 |
假设原始数据为m行n列的数据集, 其中,
(3) AHP-熵值法计算综合权重值
结合两者, 在实际应用场景中设定一个组合权系数
| $\omega = \lambda {\beta _i} + \left( {1 - \lambda } \right){\theta _i},\;i = 1,2, \cdots ,n$ | (3) |
其中,
神经网络最基本的成分是神经元, 神经元与其他神经元相连, 完成神经元之间的信息传递. 当前神经元接收到来自n个带权重的输入信号, 神经元接收到的总输入与阈值
传统的BP神经网络利用误差反向传播算法对网络进行训练, 误差反向传播算法包括信息的正向传播和误差的反向传播, 通过误差的反向传播对其网络结构中的权值与阈值进行更新, 使误差变小, 不断迭代, 直到误差小于给定期望误差时停止[14]. 算法流程如图4所示.
BP算法的主要就是对网络中的权值与阈值参数进行更新, 具体更新过程如下描述.
假设给定训练集

|
图 4 BP神经网络算法流程图 |
|
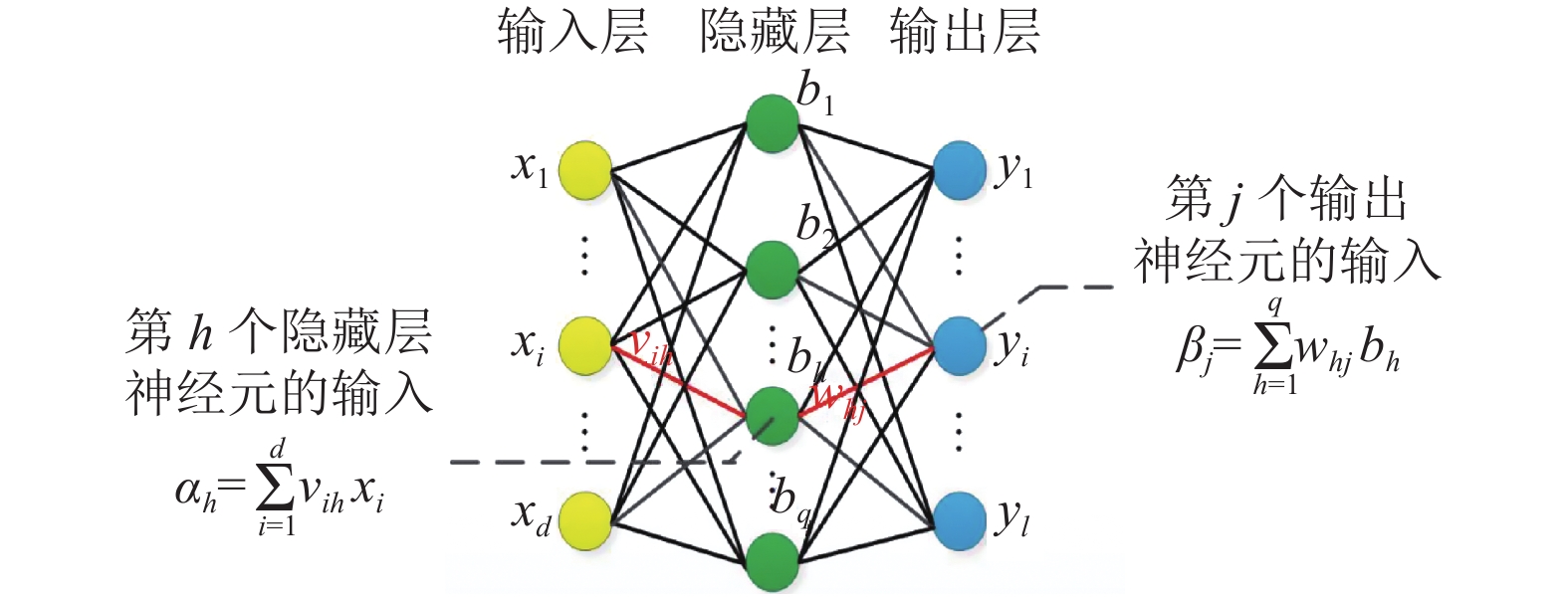
图 5 神经网络结构图 |
图5中隐藏层第h个神经元的阈值用
假定神经网络的输出为向量
| $\mathop {{y_j}}\limits^ \wedge = f\left( {{\beta _j} - {\theta _j}} \right)$ | (4) |
则均方误差为:
| ${E_k} = \frac{1}{2}\sum\limits_{j = 1}^l {{{(\mathop {{y_j}}\limits^ \wedge - {y_j})}^2}} $ | (5) |
任意参数更新估计式为:
| $v = v + \Delta v$ | (6) |
因BP算法是基于梯度下降策略的, 以目标的负梯度方向对参数进行调整, 对于均方误差
| $\Delta {w_{hj}} = - \eta \frac{{\partial {E_k}}}{{\partial {w_{hj}}}}$ | (7) |
运用链式求导法则, 有:
| $\frac{{\partial {E_k}}}{{\partial {w_{hj}}}} = \frac{{\partial {E_k}}}{{\partial \mathop {{y_j}}\limits^ \wedge }} \cdot \frac{{\partial \mathop {{y_j}}\limits^ \wedge }}{{\partial {\beta _j}}} \cdot \frac{{\partial {\beta _j}}}{{\partial {w_{hj}}}}$ | (8) |
根据
| $\Delta {w_{hj}} = \eta {g_i}{b_h}$ | (9) |
其中,
同理可得:
| $\Delta {\theta _j} = - \eta {g_i}$ | (10) |
智能制造是基于物联网、大数据、云计算等新一代信息技术, 贯穿于设计、生产、管理、服务等制造活动的各个环节, 具有信息深度自感知、智慧优化决策、精准控制自执行等功能的先进制造过程、系统与模式的总称[15]. 依据智能制造的定义以及相关智能制造企业供应商文献, 总结智能制造企业供应商特点.
(1)智能化水平高. 智能制造企业的发展要求其供应链的智能化、数字化以及信息化的建设需要进一步提升, 供应商作为供应链的一部分, 提高智能化水平势在必行.
(2)产品竞争力强. 产品竞争力包含产品质量、产品成本和产品生态化. 企业供应链中有众多的供应商, 供应商的产品竞争力会影响企业对其总体效率的评价及选择.
(3)个性化服务好. 供应商的个性化服务包含供应能力、协同创新等特征, 智能制造企业在生产过程中重点关注效率问题, 当供应货物出现服务售后等问题时, 需要快速定位并得到快速高质量的解决.
构建智能制造企业供应商评价指标体系时遵循以下5个原则: 明且突出重点性原则; 相对独立性原则; 系统全面性原则; 针对性原则; 灵活可操作性原则.
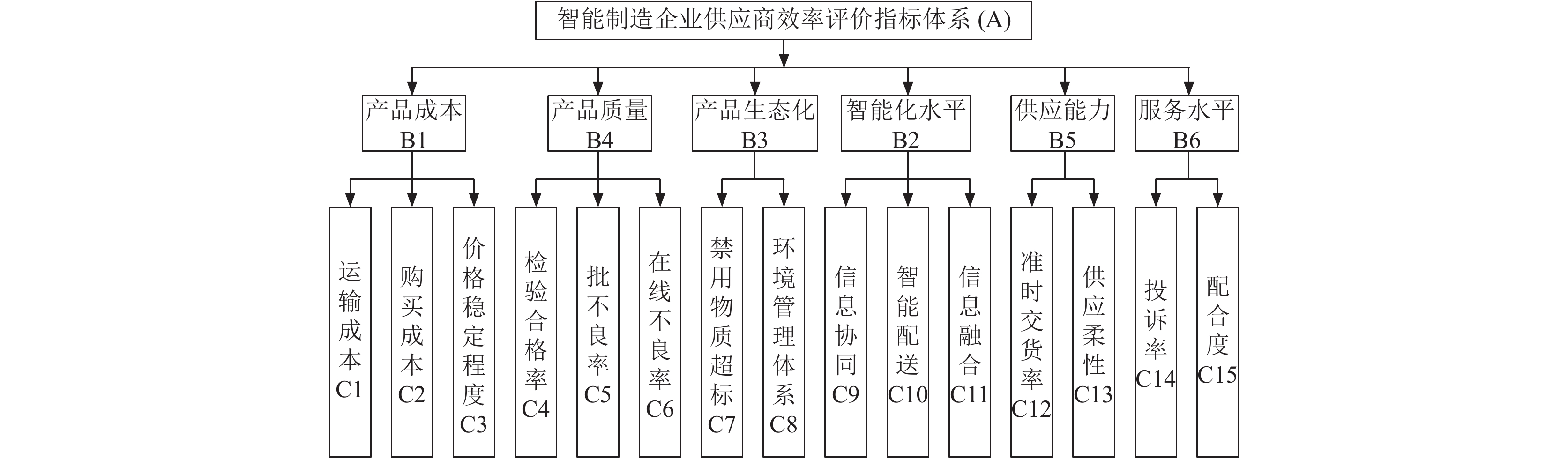
2.2 智能制造企业供应商效率评价指标体系构建最早系统研究供应商评价指标体系的学者是Dickson. 他通过与273名代理商和管理人员的统计调查, 总结出包含质量、交货等23条供应商评价指标[16]. 在Dickson的研究基础上, 越来越多的国内外学者开始对供应商评价指标开始研究. Bai CG和Sarkis J[17]以可持续发展的评价指标为中心构建了供应商评价指标体系. Cheng HY[18]从管理理念、管理体系、沟通管理、激励机制和发展战略等方面建立了供应商评价指标体系. Ruiz N等学者[19,20]为了使企业更好地适应智能制造生产, 提出了一套关于制造能力的评价指标体系. 王蒙燕[21]构建的供应商评价指标体系包含产品状况、技术能力水平、信息化程度和企业环境等. 尹峰[22]提出了包含4个层次指标的智能制造评价指标体系, 并使用AHP确定各指标权重, 对智能制造企业供应商进行评估. 张毅等[23]采用SWOT分析法, 对供应商的内部因素和外部因素进行综合分析, 建立了生鲜物品供应商评价指标体系. 从国内外文献分析来看, 质量、成本、交货、服务等都是供应商评价中的重要指标. 通过对国内外学者关于评价指标体系的研究成果的总结, 以及对智能制造企业供应商的特点分析和构建供应商效率评价指标体系原则, 从供应商效率、智能制造视角对基础指标进行重构, 形成初步的智能企业供应商评价指标体系. 智能制造企业供应商效率评价指标体系的构建是动态化的, 它随着企业智能制造能力成熟度的变化而变化, 智能制造能力成熟度越高, 对智能化要求越高. 在企业调研过程中, 发现该企业的智能制造能力成熟度处于初级发展阶段. 最终构建的指标体系包括质量、成本、服务水平、环保水平、智能化水平和供应能力等6个维度, 每个维度又细分为不同的二级指标, 如图6所示.
|
图 6 供应商评价指标体系 |
(1)产品成本
企业在采购过程中不能只看采购成本, 采购成本低的供应商不一定是最合适的, 总成本最低才是较佳的供应商, 总成本是指某原材料或者零部件在使用过程中、生命周期结束前所发生的一切支出, 包括运输成本、购买成本和价格稳定程度.
① 运输成本: 产品在运输过程中产生的所有费用.
② 购买成本: 供应商提供产品的单价.
③ 价格稳定程度: 供应商报价与基准价的变化程度.
(2)产品质量
供应商产品质量会很大影响企业对其评价度, 其考核主要从检验合格率、批不良率和在线不良率几个方面入手.
① 检验合格率: 供应商供货期间内, 进料检验合格数量除以进料检验数量所得, 计算公式如下:
| $P = \frac{q}{Q} \times 100$ | (11) |
其中, P为进料检验合格率(%), q为进料检验合格数量, Q为进料检验总数量.
② 批不良率: 在一定期间内, 所有的检验批中, 因检验判定不合格而整个检验批需要返工(或返修或报废)的批数占总的检验批的批数的比例. 计算公式如下:
| $C = \frac{a}{A} \times 100$ | (12) |
其中, C为批不良率(%), a为不良批数, A为总检验批数.
③ 在线不良率: 供应商供货期间, 企业在投入生产中, 因供应商提供的产品而导致生产出现故障的比例, 计算公式如下:
| $H = \frac{e}{E} \times 100$ | (13) |
其中, H为在线不良率(%), e为故障次数, E为整个生产次数.
(3)产品生态化
随着人们对环保意识的提高, 绿色生产变得尤其重要. 产品生态化成为制造业供应商效率评价的重要衡量指标. 包括禁用物质超标和环境管理体系.
① 禁用物质超标: 根据不同制造业的性质, 禁用物质的评价标准也是不一样的.
② 环境管理体系: 企业管理体系的一部分, 用来制定和实施其环境方针, 并管理其环境因素.
(4)智能化水平
智能制造企业需要智能化水平较高的供应商, 智能化水平体现为信息协同、智能配送和信息融合.
① 信息协同: 信息协同是指以信息为对象, 多个信息源在规定的时间和空间内, 按照统一的规则实现信息的有序流转. 包括信息共享程度、信息系统的集成水平等.
② 智能配送: 实现企业与供应商之间的快速存货、配货以及送货. 包括智能仓储、智能物流等.
③ 信息融合: 信息融合包括数据融合、数据应用、数据安全等.
(5)供应能力
制造业的订单需求往往是不确定的, 若供应商能及时的提供原材料, 可大大加强企业与效率型供应商之间的合作. 供应能力主要包括准时交货率和供应柔性.
① 准时交货率: 在一定的周期内, 按时交货的批次数量占总批次数量的比例, 准时交货对于制造方来说至关重要. 计算公式如下:
| $P = \frac{m}{M} \times 100$ | (14) |
其中, P为准时交货率(%), m为准时交货批次数, M为总批次数.
② 供应柔性: 供应柔性衡量的是其对订单变化的反映灵敏度指标, 表示的是供应商在约定的交货周期内可以接受的订单增加或减少的情况[24].
(6)服务水平
整个合作期间, 企业对供应商的满意程度, 它的衡量标准包括客户投诉率、配合程度.
① 投诉率: 合作期间, 供应商收到的投诉次数占总的合作次数的比例, 计算公式如下:
| $Z = \frac{x}{X} \times 100$ | (15) |
其中, Z为投诉率(%), x为投诉次数, X总的合作次数.
② 配合度: 业务合作中, 供应商是否积极配合以及表现出来的素质和态度.
3 基于BP神经网络的供应商效率评价模型 3.1 BP神经网络用于供应商效率评价的原理和结构设计基于BP神经网络的供应商效率评价模型主要使用一个三层的网络结构, 网络的超参数设置主要有输入层个数、隐藏层的个数、学习率和迭代次数. 输入层个数由指标体系中的叶子指标个数决定. 隐藏层的选取上需要通过计算公式
(1)数据收集. 通过企业调研、系统数据的导出以及专家和企业相关人员打分等方法收集到原始的数据集.
(2)数据预处理
由于指标数据的量纲存在差异, 不能直接将数据代入模型进行学习仿真, 需对初始数据进行标准化处理. 本文设定的指标存在正向指标和负向指标, 需根据不同性质进行不同的标准化处理, 正向指标和负向指标的标准化处理公式分别为如下.
正向指标的标准化处理公式为:
| ${{\textit{z}}_{ij}} = \frac{{{x_{ij}} - \min ({x_{ij}})}}{{\max ({x_{ij}}) - \min ({x_{ij}})}}$ | (16) |
负向指标的标准化处理公式为:
| ${{\textit{z}}_{ij}} = \frac{{\max ({x_{ij}}) - {x_{ij}}}}{{\max ({x_{ij}}) - \min ({x_{ij}})}}$ | (17) |
(3)指标权重的计算. 建立评价指标层次结构, 运用AHP-熵值法确定各指标权重.
(4) 综合效率评价值的计算. 综合效率评价值为标准化后的各指标分数与其对应的权重乘积之和. 在后续实验中, 按照综合效率评价值对供应商进行效率等级划分, 假设P为综合效率评价值, 当
(5)网络训练. 以评价指标体系中的二级指标作为输入数据, 供应商的综合效率评价值作为期望输出值, 采用误差反向传播算法训练网络.
(6)结果分析. 通过实验得出结果, 并对实验结果进行分析, 最后对供应商提出改进意见以及激励策略.
4 案例分析 4.1 数据收集选择国内某大型电池制造企业进行案例分析. 针对该企业315家ES, 采取系统数据导出和专家打分得到各指标评分, 指标分数与其对应的权重乘积之和为综合评价分. 其中运输成本、购买成本、检验合格率、批不良率、在线不良率、准时交货率和投诉率是从系统数据中处理提炼出来的, 价格稳定程度、禁用物质超标、环境管理体系、信息协同、智能配送、信息融合、供应柔性和配合度等定性指标是通过企业相关人员及相关专家采取100分制对指标进行打分收集得到. 收集到的初始数据集如表2所示.
| 表 2 初始数据集 |
4.2 数据预处理
通过上一节关于数据预处理的介绍, 运用Python语言对数据进行标准化处理. 经过处理的数据如表3所示.
4.3 计算指标权重AHP计算权重过程中, 通过专家与企业管理人员对各个指标进行量化处理, 构造对比判断矩阵如下:
| $ A = \left[ {\begin{array}{*{20}{c}} 1&{\rm{4}}&{\rm{9}}&{\rm{7}}&{\rm{5}}&{\rm{6}} \\ {{{\rm{1}}/{\rm{4}}}}&1&{\rm{7}}&{\rm{6}}&{\rm{3}}&{\rm{5}} \\ {{1/{\rm{9}}}}&{{1/{\rm{7}}}}&1&{{1/{\rm{3}}}}&{{1/{\rm{7}}}}&{{1/{\rm{5}}}} \\ {{1/{\rm{7}}}}&{{1/{\rm{6}}}}&{\rm{3}}&1&{{1/{\rm{5}}}}&{{1/{\rm{3}}}} \\ {{1/{\rm{5}}}}&{{1/{\rm{3}}}}&{\rm{7}}&{\rm{5}}&1&{\rm{3}} \\ {{1/{\rm{6}}}}&{{1/{\rm{5}}}}&{\rm{5}}&{\rm{3}}&{{1/{\rm{3}}}}&1 \end{array}} \right] $ |
| $ {B_1} = \left[ {\begin{array}{*{20}{c}} 1&{{1/5}}&{\rm{3}} \\ 5&1&{\rm{7}} \\ {{{\rm{1}}/{\rm{3}}}}&{{{\rm{1}}/{\rm{7}}}}&1 \end{array}} \right] $ |
| $\begin{split} \;\\[-8pt] {B_2} = \left[ {\begin{array}{*{20}{c}} 1&{{{\rm{1}}/{\rm{7}}}}&{{{\rm{1}}/{\rm{5}}}} \\ {\rm{7}}&1&3 \\ {\rm{5}}&{{1/3}}&1 \end{array}} \right] \end{split} $ |
| $ {B_3} = \left[ {\begin{array}{*{20}{c}} 1&{{1/7}} \\ 7&1 \end{array}} \right] $ |
| $ {B_4} = \left[ {\begin{array}{*{20}{c}} 1&{{1/3}}&{{1/7}} \\ 3&1&{{1/5}} \\ 7&5&1 \end{array}} \right] $ |
| $ {B_5} = \left[ {\begin{array}{*{20}{c}} 1&4 \\ {{1/4}}&1 \end{array}} \right] $ |
| $ {B_6} = \left[ {\begin{array}{*{20}{c}} 1&{{1/3}} \\ 3&1 \end{array}} \right] $ |
| 表 3 标准化处理数据集 |
熵值法计算指标权重时, 需使用标准化处理后的数据. 本文根据二八原则, 计算过程中设
| 表 4 AHP-熵值法 |
4.4 综合效率评价值的计算
利用AHP-熵值法计算得出的权重和标准化后的数据, 各指标分数与其对应的权重乘积之和即为综合效率评价值, 计算结果如表4.
4.5 网络训练选取表3数据中的前300条数据进行模型的训练, 后15条数据用于测试检验. 将归一化到[0, 1]区间的数据输入到用Matlab构造的BP神经网络模型中, 其中输入神经元个数为15, 隐藏层神经元个数20, 输入层到隐藏层使用“tansig”函数, 隐藏层到输出层使用的激活函数为“purelin”, 使用的训练函数为“traingda”, 设置最大迭代次数为5000, 学习率0.01. 经过107次的迭代, 训练达到预期想要的结果. 预测综合效率评价值与期望输出值之间的对比图, 如图7所示.

|
图 7 预测综合效率评价值与期望综合效率评价值对比图 |
图7中, R2表示决定系数, 它用来判断回归方程拟合程度, 其值越趋近于1, 估计的值就越精确. 通过图示可以看出, 预测值与期望输出值近乎重合, 此实验结果比较理想.
神经网络有过拟合的缺陷, 为防止过拟合, 本文利用Matlab, 把数据划分为training、validation和test, Regression训练图如图8所示.

|
图 8 Regression训练图 |
图8中横坐标为目标值, 纵坐标为网络的输出值. 通过图示可以看出, 4幅图的曲线都在对角线上, 这是一种比较理想的实验结果, R表示测量输出与目标之间的相关性, 1表示密切相关, 0表示随机相关, 本文实验R都达到0.9以上, 很好的保证了其相关性.
4.6 结果分析期望输出值与预测输出值的结果及其误差如表5所示.
| 表 5 预测值与期望输出值比较 |
通过实验结果得到, 期望输出值与预测值之间最大误差为0.0025, 完全满足智能制造企业供应商效率评价的需要. 将训练好的模型存入知识库中, 用时只需在供应商管理系统中输入将要评价供应商的各项二级指标属性值矩阵, 即可得到综合评价指标数据, 避免了确定指标权重的随意性和人为因素, 提高评价决策的效率.
测试的15家供应商中, S307和S314为一级效率型供应商, 综合效率高. 而S301和S304为五级效率型供应商, 综合效率弱. S301和S304供应商供给产品合格率不错, 且供货及时, 但是其产品的批不良率和在线不良率都比较差、成本较高、产品价格经常会发生浮动, 需要在成本和质量上进行大的整改. 企业需对其提出改进意见, 否则会给企业的经济效益带来直接或间接影响. 若在企业限定时间内供应商未达到整改要求, 企业则会根据实际需要与其停止合作并从潜在供应商中挑选优秀的供应商进行合作. S307和S314供应商提供的产品其检验合格率和供货速度都有所欠缺, 但是成本和生产过程中的产品质量上都有一定的保障, 尤其是在成本上, 可以较大的提高企业的生产利益, 企业在后续制造过程中, 可以采取一定的精神激励以及物质激励, 对其提高采购份额、签订长期合同以及产品免检等措施, 激励其做的更加出色.
5 结论与展望智能制造企业供应商效率评价对于国内智能制造业的发展有重要意义. 本文扎根于智能制造企业的研究, 根据智能制造企业供应商的特点、评价指标体系构建原则和文献总结, 构建智能制造企业供应商效率评价指标体系, 运用AHP-熵值法计算指标权重. 智能制造企业供应商评价指标之间呈现出复杂的非线性关系, 充分利用从企业中获取到的智能制造企业工业大数据, 使用BP神经网络模型对其进行训练, 尊重数据的客观性, 有效降低人为主观成分, 提高评价的科学性和合理性. 通过最终的实例验证得出数据驱动下的基于BP神经网络模型对智能制造企业供应商效率评价有一定的指导意义, 能够有效地对供应商效率及合作中存在的问题进行实时监控和反馈管理.
本项研究还存在一些缺陷, 如BP神经网络的训练需大量的数据, 后期研究中, 需搜索更多的数据对网络进行训练及测试. BP神经网络存在精度、稳定度的问题, 需要进行优化操作. 指标体系构建时针对性太强, 普适性较弱. 这些问题需要我们在今后的研究中进行不断的探索.
| [1] |
徐雪, 张艺, 余开朝. 基于BP神经网络的智能制造能力评价研究. 软件, 2018, 39(8): 162-166. |
| [2] |
张曙. 工业4.0和智能制造. 机械设计与制造工程, 2014(8): 1-5. |
| [3] |
Yurdakul M, İç YT. Development of a performance measurement model for manufacturing companies using the AHP and TOPSIS approaches. International Journal of Production Research, 2005, 43(21): 4609-4641. DOI:10.1080/00207540500161746 |
| [4] |
Eckert-Gallup AC, Sallaberry CJ, Dallman AR, et al. Application of Principal Component Analysis (PCA) and improved joint probability distributions to the Inverse First-Order Reliability Method (I-FORM) for predicting extreme sea states. Ocean Engineering, 2016, 112: 307-319. DOI:10.1016/j.oceaneng.2015.12.018 |
| [5] |
Chen TW, Lin JY, Chen KS. Selecting a supplier by fuzzy evaluation of capability indices, CPM. The International Journal of Advanced Manufacturing Technology, 2003, 22(7-8): 534-540. DOI:10.1007/s00170-002-1487-8 |
| [6] |
Cannavacciuolo L, Iandoli L, Ponsiglione C, et al. An analytical framework based on AHP and activity-based costing to assess the value of competencies in production processes. International Journal of Production Research, 2012, 50(17): 4877-4888. DOI:10.1080/00207543.2012.657974 |
| [7] |
Zhao JJ, He YH, Huang RQ, et al. Weights of slope stability evaluation indexes based on factor analysis method. Journal of Southwest Jiaotong University, 2015, 50(2): 325-330. |
| [8] |
Loh HS, Zhou QJ, Thai VV, et al. Fuzzy comprehensive evaluation of port-centric supply chain disruption threats. Ocean & Coastal Management, 2017, 148: 53-62. |
| [9] |
Sun WH, Li D, Liu P. A decision-making method for sponge city design based on grey correlation degree and TOPSIS method. Journal of Interdisciplinary Mathematics, 2018, 21(4): 1031-1042. DOI:10.1080/09720502.2018.1456826 |
| [10] |
郭彤颖, 陈露. 基于鸟群算法优化BP神经网络的热舒适度预测. 计算机系统应用, 2018, 27(4): 162-166. DOI:10.15888/j.cnki.csa.006303 |
| [11] |
(奥)Schuh C, (奥)Strohmer MF, (英)Easton S, 等. 供应商关系管理 机会与价值最大化. (美)李学芸, 吴江, 译. 北京: 清华大学出版社. 2016.
|
| [12] |
孟卫东, 龙美彪. 曲线数据压缩算法的研究及应用. 计算机系统应用, 2019, 28(5): 150-155. DOI:10.15888/j.cnki.csa.006949 |
| [13] |
宗宸生, 郑焕霞, 王林山. 改进粒子群优化BP神经网络粮食产量预测模型. 计算机系统应用, 2018, 27(12): 204-209. DOI:10.15888/j.cnki.csa.006651 |
| [14] |
卢滢宇. 竞争算法优化BP神经网络性能研究. 计算机系统应用, 2019, 28(5): 173-177. DOI:10.15888/j.cnki.csa.006903 |
| [15] |
中国电子技术标准化研究院. 智能制造能力成熟度模型白皮书1.0版. 北京: 中国电子技术标准化研究院, 2016.
|
| [16] |
Dickson GW. An analysis of vendor selection systems and decisions. Journal of Purchasing, 1966, 2(1): 5-17. DOI:10.1111/j.1745-493X.1966.tb00818.x |
| [17] |
Bai CG, Sarkis J. Integrating sustainability into supplier selection with grey system and rough set methodologies. International Journal of Production Economics, 2010, 124(1): 252-264. DOI:10.1016/j.ijpe.2009.11.023 |
| [18] |
Cheng HY. Research on comprehensive evaluation model of supplier management performance. Logistics Sci-Tech, 2012, 35(1): 74-78. |
| [19] |
Frankowiak M, Grosvenor R, Prickett P. A review of the evolution of microcontroller-based machine and process monitoring. International Journal of Machine Tools and Manufacture, 2005, 45(4–5): 573-582. DOI:10.1016/j.ijmachtools.2004.08.018 |
| [20] |
Ruiz N, Giret A, Botti V, et al. An intelligent simulation environment for manufacturing systems. Computers & Industrial Engineering, 2014, 76: 148-168. |
| [21] |
王蒙燕. 基于ELECTRE-IV的国际贸易目标供应商评价算法. 统计与决策, 2014(23): 52-55. |
| [22] |
尹峰. 智能制造评价指标体系研究. 工业经济论坛, 2016, 3(6): 632-641. |
| [23] |
张毅, 袁颖, 狄龙. 大型超市生鲜物品供应商评价选择研究. 科技通报, 2017, 33(8): 133-136, 242. |
| [24] |
江志娟. 基于BP神经网络和合作博弈的供应商评价选择研究[硕士学位论文]. 沈阳: 东北大学, 2008.
|
 2020, Vol. 29
2020, Vol. 29



