图像融合是将在同一场景下的不同聚焦的两幅或者多幅图像的信息进行冗余互补, 从而形成一张具有完整信息的图像. 图像融合在许多领域都具有广泛的应用, 例如在医学医疗方面和遥感图像的融合等方面. 现如今, 存在的图像融合方法有很多种, 其中比较常用的方法是基于分辨率分解的图像融合, 基于分辨率分解的方法又有多种, 例如基于图像金字塔分解[1,2]的方法、基于小波变换[3]的方法、基于相位一致性和方向对比度的非子采样轮廓线变换的融合方法[4]、基于稀疏表示的同时进行正交匹配跟踪的融合[5]方法等等, 但是上述的方法中的一些方法对采集的图像有很大的要求, 这就意味着对采集图像的传感器有着很大的负担, 而且有些方法在计算上很复杂. 基于以上不足, 本文提出来了一种基于孪生卷积神经网络的图像融合方法.
卷积神经网络(Convolutional Neural Network, CNN)[6-8]是人工神经网络和深度学习这两者的完美结合, 其通过反向传播算法[9]来训练其中的权值, 进而实现我们所想要的结果. 卷积神经网络有很多优点, 例如, 有比较好的容错性能、自适应性能、比较好的自学能力等等. 由于卷积神经网络以上的优点, 将原来传统的卷积神经网络改进为孪生卷积神经网络, 孪生卷积神经网络在实质上就是一个双通道的卷积神经网络, 并且为了计算简单, 本文算法将其中的一个卷积层换成了残差网络层.
2 Siamese 网络“Siamese”网络是Bromley J、Guyon I等在1993年在第一次提出来的[10]. 又在2005年由Chopra S、Hadse R等[11]进行了补充, 在其文章中用孪生网络进行了人脸相似性判别, 将Siamese网络分成两部分, 前半部分用于特征提取, 将两张图片输入进网络中输出两个特征向量, 后半部分用构造的特征向量进行距离度量, 计算输入图像的相似度以判别人脸的相似性. 后又由Zagoruyko S和Komodakis N在文献[12]中以Siamese网络为原始基础进行了改进, 首次将空间金字塔池化(Spatial Pyramid Pooling, SPP)和Siamese网络进行了结合[13].
Siamese网络可以理解成是一种衡量相似性的算法, 当要分类的类别很多但是每一个类别所对应的样本数目很少的时候可以用于分类. Siamese网络在近年来多应用于人脸识别以及相似度检测. 本文所提的方法是基于Siamese网络进行特征的提取从而生成一个特征向量. Siamese网络有两个分支, 并且两个分支的权重和结构是一样的. Siamese网络具体的结构如图1所示, 将原图片X1、X2送入到系统当中, 判断X1和X2是否是同一图片, W是系统共享的学习参数, GW{X1}和GW{X2}是生成低维空间中的X1和X2的两点映射, 这样就可以通过计算GW{X1}和GW{X2}两者之间的距离来判断X1和X2是否是同一张图片了.

|
图 1 Siamese原始网络结构图 |
3 本文所用网络 3.1 本文所用的孪生卷积神经网络
本文所采用的Siamese网络是文献[12]中提及网络模型的改进版, 本文网络用了两个完全相同的卷积神经网络, 其中这两个网络是权值共享.
图2给出的是图像融合算法的前一部分特征提取的网络图, 这是一个Siamese CNN[14]网络图, 其中左右两边的两个部分在结构上是完全一样的, 并且共享相同的参数, 即权重和偏置.
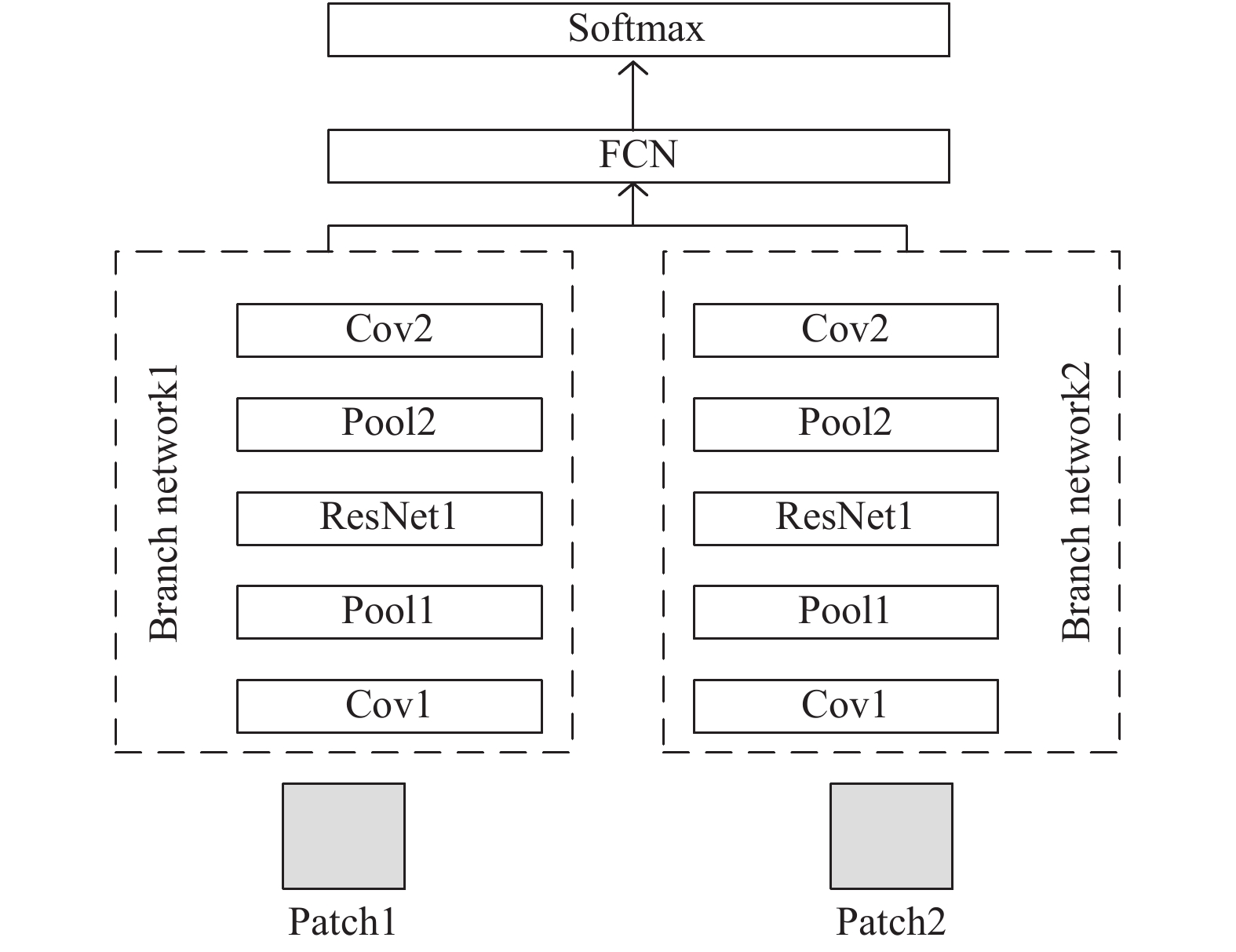
|
图 2 本文所使用的Siamese网络结构图 |
本文网络是由两个卷积层, 两个池化层, 一个残差块以及一个全连接层组成的. 在本文中我们将原本孪生网络中的一个卷积层换成了残差网络[15,16], 所用的残差网络的结构如图3所示. 输入的patch为16×16, 即卷积层和池化层的通道数都是16(即卷积模板为16种), 其卷积核的大小为3×3, 池化窗口尺寸为2×2, 卷积方式为零填充(zero padding), 卷积层的激活函数为Relu, 并且子CNN输出的是256维特征向量, 每个池化层包括跨信道归一单元. 首先将输入的patch的空间大小调整为16×16, 然后对网络进行训练以最大损失函数为优化目标(损失函数如式(1), 采用随机梯度下降(Stochastic Gradient Descent, SGD)[17]的方法使其最大损失函数最小化; 第二步将拼接完成的512个特征图直接连接在二维向量上面; 最后, 将连接生成的这个二维向量作为输入, 输出给一个双向的Softmax层, 其中Softmax可以用于分类, 输出的是类别的概率分布, 网络在Softmax层生成了两类的概率分布, 这两个类别分别对应的是归一化之后的权重分配的结果. 由于本文的网络是具有全连接的, 所以输入和输出的数据都是固定尺寸的, 其模型配置如表1所示.
| $\left\| {{X_i} - {X_j}} \right\|_M^2 = {\left( {{X_i} - {X_j}} \right)^{\rm T}}M\left( {{X_i} - {X_j}} \right)$ | (1) |
其中,

|
图 3 残差网络结构图 |
| 表 1 模型配置 |
我们首先将全连通层转换为包含两个大小为3×3×512的核的等效卷积层, 转换后, 网络可以将任意大小的原图像作为一个整体进行处理, 生成一个密集的预测图, 其中每个预测(一个二维向量)包含对应位置的patch对的相对清晰信息. 由于每个预测中只有两个维度, 并且它们的和被标准化为1, 因此输出可以简化为第一个(或第二个)patch的权重. 最后, 为了得到与原图像大小相同的权值图, 我们将该值赋值为patch位置内所有像素的权值, 并对重叠的像素进行平均, 最后得到最终的权重图.
3.2 融合过程整个的图像融合过程可以分为两个部分, 第一个部分用孪生卷积神经网络进行图片信息的提取得到一个权重图, 这一部分的详细描述在3.1章节; 第二部分是利用金字塔分解后再融合, 具体融合过程如图4所示, 先将第一部分得到的权重图W经过高斯金字塔变换得到G{W},再将两张待融合图片A和B进行拉普拉斯变换分别得到L{A}和L{B}, 再将得到的G{W}和L{A}、L{B}分别进行融合, 得到L{C}和L{D}, 再将L{C}和L{D}进行融合得到L{F}, 最中将L{F}进行拉普拉斯反变换得到最终的融合图像F.

|
图 4 融合过程图 |
对于每一个分解层, 需要计算其
| $\left\{\begin{array}{l} E_A^l\left( {x,y} \right) = {\displaystyle\sum\limits_m {\sum\limits_n {L\left\{ A \right\}} } ^l}{\left( {x + m,y + n} \right)^2}, \\ E_B^l\left( {x,y} \right) = {\displaystyle\sum\limits_m {\sum\limits_n {L\left\{ B \right\}} } ^l}{\left( {x + m,y + n} \right)^2} \\ \end{array} \right.$ | (2) |
其中,
融合模式测定中的相似度测量可以表示为式(3):
| ${S^l}\left( {x,y} \right) = \frac{{2\displaystyle\sum\limits_m {\displaystyle\sum\limits_n {L{{\left\{ A \right\}}^l}\left( {x + m,y + n} \right)L{{\left\{ B \right\}}^l}\left( {x + m,y + n} \right)} } }}{{E_A^l\left( {x,y} \right) + E_B^l\left( {x,y} \right)}}$ | (3) |
其范围为[–1,1], 若测量相似度为1, 则说明两者具有高度相似性.t表示了融合模式测定中的阈值, 若
| $\left\{\begin{array}{l} L{\left\{ C \right\}^l}\left( {x,y} \right) = G{\left\{ W \right\}^l}\left( {x,y} \right) \cdot L{\left\{ C \right\}^l}\left( {x,y} \right) \\ L{\left\{ D \right\}^l}\left( {x,y} \right) = G{\left\{ W \right\}^l}\left( {x,y} \right) \cdot L{\left\{ B \right\}^l}\left( {x,y} \right) \\ L{\left\{ F \right\}^l}\left( {x,y} \right) = G{\left\{ W \right\}^l}\left( {x,y} \right) \cdot L{\left\{ B \right\}^l}\left( {x,y} \right) \\ \end{array}\right. $ | (4) |
如果
| $ L{\left\{ F \right\}^l}\left( {x,y} \right) = \left\{ \begin{aligned} &{L{{\left\{ A \right\}}^l}\left( {x,y} \right),{\rm if}\;E_A^l\left( {x,y} \right) \ge E_B^l\left( {x,y} \right)}\\ &{L{{\left\{ B \right\}}^l}\left( {x,y} \right),{\rm if}\;E_A^l\left( {x,y} \right) < E_B^l\left( {x,y} \right)} \end{aligned} \right. $ | (5) |
最后, 对
为了验证本文方法的有效性, 使用3组图像对网络模型的性能进行测试. 这3组图像分为3类, 第1类是医学图像组合(如图5所示), 包括一张计算机断层扫描(CT)图像和一张核磁共振图像(MRI); 第2类是风景图片(如图6所示), 包括两张不同焦点的两张豹子的图片; 第3类是花草图像(如图7所示), 包含了两张不同焦点的花草图像. 本文所有的实验均在Lenovo CORE i5 Bth Gen下的Matlab 2016A的版本下完成.
在实验中, 为更好测试本文方法的可实用性, 选用两种现存图像融合方法和本文图像融合方法进行比较, 且比较了原始Siamese CNN网络结构的结果和改进后Siamese CNN网络的结果. 现存两种图像融合方法分别是基于导向滤波(Guided Filtering, GF)[18]的图像融合方法、基于小波变换(Wavelet Transform, WT)[19]的图像融合方法. 仅从医学图像的融合结果分析, 可明显看出来本文方法具有更高的对比性, 基于小波变换方法的图像看起来存在很多噪声, 从视觉效果上来说不如本文方法. 3种类型图片融合结果如图8至图10所示.

|
图 5 医学图像 |

|
图 6 风景不同对焦图像 |

|
图 7 花草不同对焦图像 |
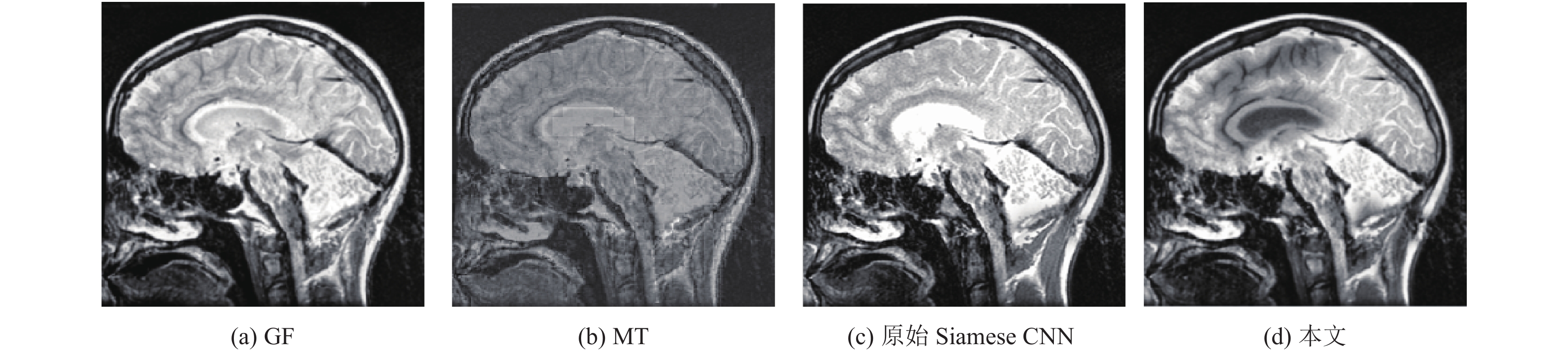
|
图 8 医学图像融合结果 |
由于本文实验图像是没有参考图像的, 为了能够更加客观的表示对比的方法和本论文的方法,选取了几个客观的无参考图像情况下的图像融合评价标准. 第一个是互信息(MI), 互信息作为信息论中的一个很重要的概念, 可以用来度量两个变量之间的相关性程度, 在评价融合时可以表示融合之后的图像包含原始图像的信息总量, 这个值越大, 就表示融合之后的图像包含的原始图像的信息越多, 融合效果越好, 在本文的实验中互信息的结果是融合图像分别和两个待融合图像的互信息之和; 第二个是平均梯度(AG), AG描述了融合之后图像的清晰度; 第三个是边缘强度(ES), ES描述了融合之后图片的边缘信息, ES越大就说明边缘信息越多. 最后给出了所有的方法在CPU上的运行时间以作参考. 对比结果如表2所示.

|
图 9 风景图像融合结果 |

|
图 10 花草图像融合结果 |
| 表 2 对比说明 |
从表2中可见,本文所用方法融合之后的图像的互信息和平均梯度的数值都要大于用小波变换和导向滤波的数值, 那就说明本文所提方法在融合之后的图像包含原图像的信息度上和清晰度上都要优于小波变换和导向滤波的图像融合. 但是在边缘信息的包含量上, 在风景和花草这两类上面, 本文所提的方法略逊于小波变换和导向滤波. 但是单就视觉效果上来说, 本文方法所得到的融合图像在视觉效果上要比其他两种办法好. 与原始的网络结构相对比, 在包含原图片的信息、融合图片的清晰度、和融合图片的边缘信息上与改进之后的实验结果相差不大, 但是在运行时间上却是大大的加快了, 说明改进之后的方法在时效性上更好. 综上所述, 本文所提出的方法是具有一定的实用性的.
5 结论本文提出了一种基于改进的卷积神经网络的像素级的图像融合方法, 将原本孪生神经网络中的一个卷积层换成了残差块, 比原本的算法更为简略, 并且实验所用的时间更短, 实现了像素级的图像融合. 首先, 用孪生卷积神经网络进行了图像的特征提取; 然后, 用图像金字塔对多尺度特征进行融合; 最后, 与现存的传统的两种图像融合的方法进行了比较; 侧面印证了本文方法的可实施性和可取之处. 但是本文所提方法融合之后的图像的边缘信息包含量不如基于小波变换的图像融合, 在这一点上有待改进.
| [1] |
李增祥, 漆志亮, 贾楠, 等. 基于小波图像金字塔的工件目标检测与定位研究. 现代电子技术, 2019, 42(15): 33-37. |
| [2] |
余美晨, 孙玉秋, 王超. 基于拉普拉斯金字塔的图像融合算法研究. 长江大学学报(自科版), 2016, 13(34): 21-26. |
| [3] |
刘羽, 汪增福. 结合小波变换和自适应分块的多聚焦图像快速融合. 中国图象图形学报, 2013, 18(11): 1435-1444. DOI:10.11834/jig.20131106 |
| [4] |
王瑞瑞, 马建文, 石伟, 等. 结合非子采样轮廓变换和形态收缩算子的多源遥感影像配准. 农业工程学报, 2012, 28(19): 110-118. DOI:10.3969/j.issn.1002-6819.2012.19.015 |
| [5] |
杨勇, 闫钧华, 井庆丰. 融合图像显著性与特征点匹配的形变目标跟踪. 中国图象图形学报, 2018, 23(3): 384-398. DOI:10.11834/jig.170339 |
| [6] |
Khan A, Sung JE, Kang JW. Multi-channel fusion convolutional neural network to classify syntactic anomaly from language-related ERP components. Information Fusion, 2019, 52: 53-61. DOI:10.1016/j.inffus.2018.10.008 |
| [7] |
Liu Y, Chen X, Cheng J, et al. A medical image fusion method based on convolutional neural Networks. Proceedings of 2017 20th International Conference on Information Fusion. Xi’an, China. 2017. 1–7.
|
| [8] |
Zhang Y, Liu Y, Sun P, et al. IFCNN: A general image fusion framework based on convolutional neural network. Information Fusion, 2020, 54: 99-118. DOI:10.1016/j.inffus.2019.07.011 |
| [9] |
Sun W, Huang CC. A carbon price prediction model based on secondary decomposition algorithm and optimized back propagation neural network. Journal of Cleaner Production, 2020, 243: 118671. DOI:10.1016/j.jclepro.2019.118671 |
| [10] |
Bromley J, Guyon I, LeCun Y, et al. Signature verification using a “Siamese” time delay neural network. Proceedings of the 6th International Conference on Neural Information Processing Systems. San Francisco, CA, USA, 1993, 737-744. |
| [11] |
Chopra S, Hadsell R, LeCun Y. Learning a similarity metric discriminatively, with application to face verification. Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA, USA, 2005, 539-546. |
| [12] |
Zagoruyko S, Komodakis N. Learning to compare image patches via convolutional neural networks. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA, 2015, 4353-4361. |
| [13] |
He KM, Zhang XY, Ren SQ, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1904-1916. DOI:10.1109/TPAMI.2015.2389824 |
| [14] |
Wang B, Wang L, Shuai B, et al. Joint learning of Siamese CNNs and temporally constrained metrics for tracklet association. arXiv: 1605.04502v2, 2016.
|
| [15] |
李成, 汪小凯, 章振原, 等. 基于深度残差网络的有色金属破碎料视觉识别方法. 有色金属工程, 2019, 9(8): 127-134. DOI:10.3969/j.issn.2095-1744.2019.08.018 |
| [16] |
Wu ST, Zhong SH, Liu Y. Deep residual learning for image steganalysis. Multimedia Tools and Applications, 2018, 77(9): 10437-10453. DOI:10.1007/s11042-017-4440-4 |
| [17] |
Sreela SR, Idicula SM. Action recognition in still images using residual neural network features. Procedia Computer Science, 2018, 143: 563-569. DOI:10.1016/j.procs.2018.10.432 |
| [18] |
Wang Q, Zhang L, Zou WB, et al. Salient video object detection using a virtual border and guided filter. Pattern Recognition, 2020, 97: 106998. DOI:10.1016/j.patcog.2019.106998 |
| [19] |
王华兵, 邱春荣, 宫蓉蓉. 基于小波变换的图像融合算法比较研究. 长沙民政职业技术学院学报, 2018, 25(3): 129-131. |
 2020, Vol. 29
2020, Vol. 29



