随着无线定位技术的不断发展, 基于位置服务的研究越来越受到了人们的关注^[1]. 目前, 全球定位系统(Global Positioning System, GPS)已被广泛应用于室外定位^[2], 但由于墙体等建筑物对卫星信号遮挡, 其在室内环境下定位效果较差. 因此, 室内定位技术不断涌现, 比如Zigbee、UWB、WIFI、RFID等定位技术^[3]. 其中UWB是一种穿透力强、抗干扰能力强的无线定位技术, 比WIFI、ZigBee、RFID等室内无线定位技术有着更高的定位精度, 在视距(los of sight, LOS)情况下可达厘米级别定位精度且不存在误差累积, 然而在复杂的室内环境中, UWB信号在传播过程中不可避免地产生多径效应, 从而导致明显的NLOS定位误差^[4-8]. 而DR是一种具有自主定位导航能力并且短时定位高精度的技术, 但其定位结果将会随着时间的推移发生飘移, 即存在定位误差累积的问题^[9].

针对上述问题, 本文提出了一种基于UKF的环境自适应UWB/DR室内定位方法, 将UWB定位和DR定位的优势联合, 用DR定位降低UWB定位出现的NLOS误差, 用UWB定位更新DR定位的当前位置, 减少DR定位的累积误差. 该方法通过建立自适应UKF滤波模型, 将UWB定位信息和DR定位信息进行融合. 在此过程中, 利用新息和高斯分布的 $3\sigma $ 原则来对UWB定位结果进行非视距检测, 再通过新息的实时估计协方差和理论协方差来构建环境适应系数, 进而用此系数动态修正UWB定位的观测噪声, 使得观测噪声自适应真实环境, 更大程度地降低NLOS误差对融合定位结果的影响. 为了验证本文定位方法的有效性和稳定性, 设计差速移动机器人在多遮挡室内环境中进行折线运动实验并实时采集和处理数据. 实验效果表明, 该方法能够有效减小UWB定位的NLOS误差和DR定位的累积误差, 并且由于环境适应系数的创新引入, 比UKF定位方法和PF定位方法具有更高的定位精度和更强的抗NLOS误差性能.

1 DR定位

DR定位是一种精度较高的自主式定位方法, 尤其适用于短时短距定位. 其核心思想可概述为根据当前时刻的位置、速度和航向推算下一时刻的位置. 航位推算的实现原理如图1所示.

已知当前时刻的初始位置 $\left( {{x_{{k}}}, {y_k}} \right)$ 、航向角 ${\theta _k}$ 和速度 ${v_k}$ , 移动机器人在下一时刻移动到 $\left( {{x_{k + 1}}, {y_{k + 1}}} \right)$ 时, 航向角的变化为 ${\omega _k}$ , 根据当前的速度 ${v_k}$ 乘以间隔时间 ${t_{k + 1}} - {t_k}$ 得到的航行距离 ${l_k}$ , 从而 ${t_{k + 1}}$ 时刻的位置和航向角可以表示为:

$\left\{ {\begin{array}{*{20}{l}} {{x_{k + 1}} = {x_k} + {v_k}.\left( {{t_{k + 1}} - {t_k}} \right).\sin{\theta _k}} \\ {{y_{k + 1}} = {y_k} + {v_k}.\left( {{t_{k + 1}} - {t_k}} \right).\cos{\theta _k}} \\ {{\theta _{k + 1}} = {\theta _k} + {w_k}} \end{array}} \right.$

(1)

采用的数据采集移动平台如图2所示. 该移动平台采用差速驱动, 左右两个为直流电机驱动的主动轮, 前后两个为用于支撑的万向轮. 本文通过安装在电机轴端的光电编码器输出来进行航位推算.

设车轮的直径为D, 两车轮间距为L, 左右两个驱动轮的转速分别为 ${\omega _l},\;{\omega _r}$ , 根据差速移动机器人的运动学关系^[10]可知速度和航向变化的计算表达式为:

$\left\{\begin{array}{l} v = \dfrac{{\left( {{w_R} + {w_L}} \right)}}{2}D \\ w = \dfrac{{\left( {{w_R} - {w_L}} \right)D}}{L} \\ \end{array} \right.$

(2)

因此k时刻根据的位置和航向推得的下一时刻的位置和航向可表达为:

$\left\{ {\begin{array}{*{20}{l}} {{x_{k + 1}} = {x_k} + D\dfrac{{\left( {{w_{{L_k}}} + {w_{{R_k}}}} \right)}}{2}\left( {{t_{k + 1}} - {t_k}} \right).\sin{\theta _k}} \\ {{y_{k + 1}} = {y_k} + D\dfrac{{\left( {{w_{{L_k}}} + {w_{{R_k}}}} \right)}}{2}\left( {{t_{k + 1}} - {t_k}} \right).\cos{\theta _k}} \\ {{\theta _{k + 1}} = {\theta _k} + D\dfrac{{\left( {{w_{{L_k}}} - {w_{{R_k}}}} \right)}}{L}} \end{array}} \right.$

(3)

其中, ${\omega _{{R_k}}},\;{\omega _{{L_k}}}$ 分别表示左右驱动轮 ${t_i}$ 时刻的转速, 由光电编码器测得.

2 基于TOA的UWB定位

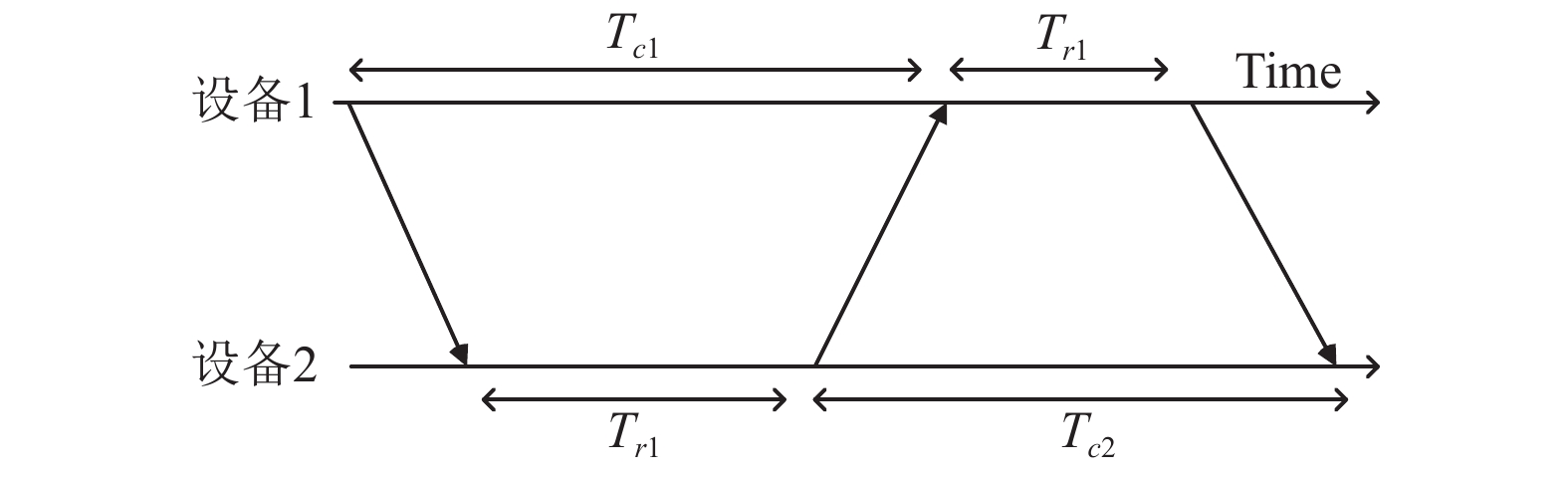
到达时间方法(Time Of Arrive, TOA)的核心在于精确地测量出信号从发射机到达接收机的飞行时间. 已知信号的传播速度即可精确地计算出发送机和接收机的之间的距离, 但是发射机和接收机采用不同的时钟源, 即两者存在影响飞行时间测量值的时钟差, 又因为信号传播速度非常快, TOA所测距离准确度难以保证. 因此采用DS测距(Double-Sided two-way ranging)消除时钟差影响, 其原理图如图3所示.

图3中, ${T_{c1}},\;{T_{c2}}$ 分别表示设备1和设备2发出信号到收到回应信号所耗费的时间, ${T_{r1}},\;{T_{r2}}$ 则分别表示设备1和设备2处理收到的信号所耗费的时间, c为光速, 从而可得待测节点到四周各个基站的距离为:

${{{d}}_i} = \dfrac{{\left( {{T_{c1}}.{T_{c2}}{\rm{ - }}{T_{{\rm{r}}1}}.{T_{r2}}} \right)}}{{{T_{c1}} + {T_{c2}} + {T_{{\rm{r}}1}} + {T_{r2}}}}c$

(4)

该方法等效于分别用设备发射机和接收机的时钟计算一次来回路程花费的时间, 再四均等分总时间求取测量时间. 这可以有效减少不同设备之间的时钟差导致的飞行时间误差, 极大提高了TOA的精度.

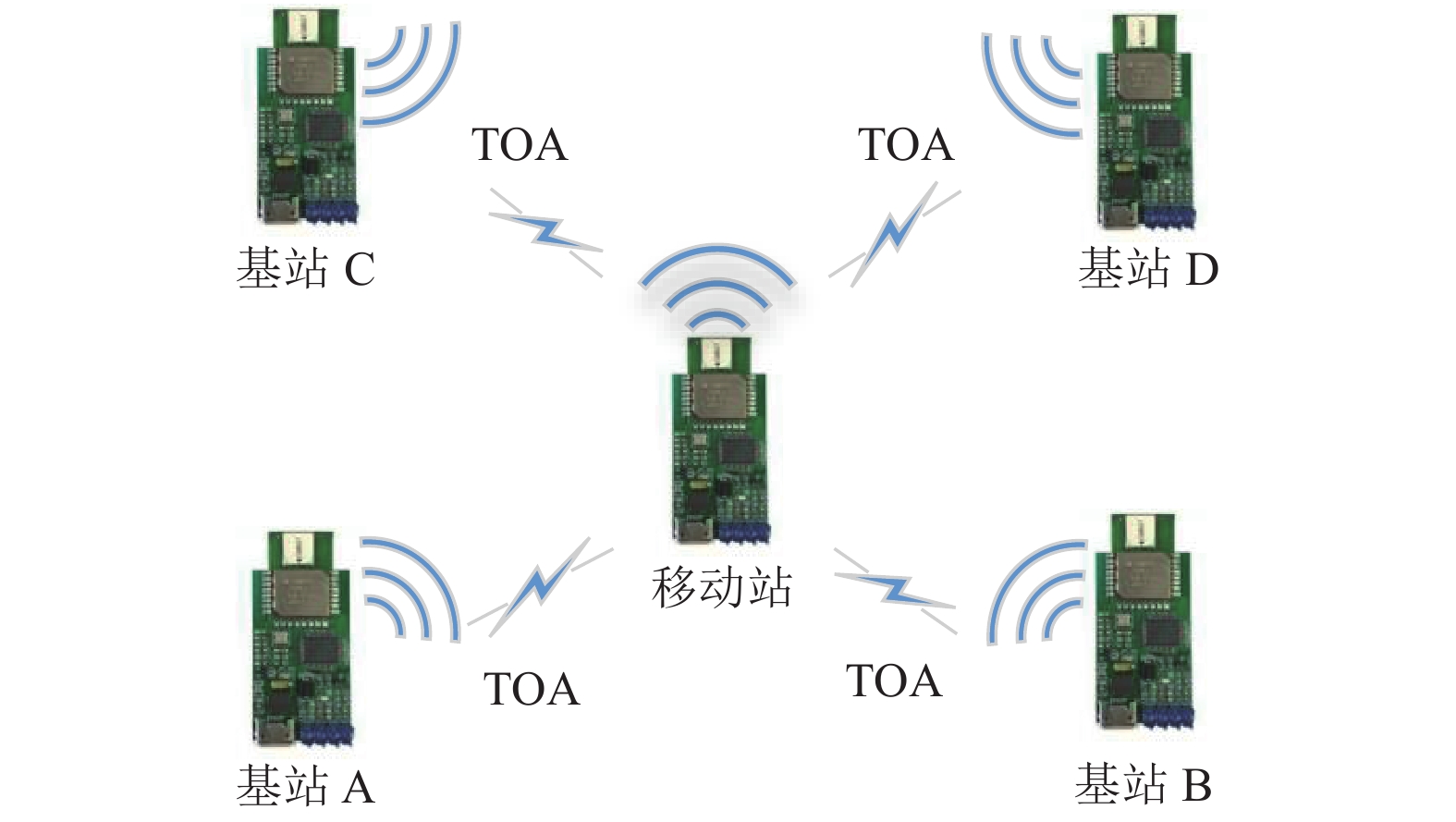
本文所采用的UWB定位系统的原理如图4所示, 移动站安装在数据采集移动平台上, 定位系统的基准锚点为四周的4个定位基站, 基站基于TOA方法实时获取其到移动站的距离.

令UWB移动站(Moving Station, MS)和基站(Base Station, BS)的位置分别为 $(x, y)$ 和 $({x_i}, {y_i})$ , MS和BS的距离为 ${d_i}$ , 因此可得方程组为:

$\left\{ \begin{array}{l} \sqrt {{{(x - {x_1})}^2} + {{(y - {y_1})}^2}{\rm{ }}} {\rm{ = }}{{{d}}_1} \\ \sqrt {{{(x - {x_2})}^2} + {{(y - {y_2})}^2}{\rm{ }}} {\rm{ = }}{{{d}}_2} \\ \quad\quad\quad\quad\quad\vdots \\ \sqrt {{{(x - {x_i})}^2} + {{(y - {y_i})}^2}{\rm{ }}} {\rm{ = }}{{{d}}_i} \\ \end{array} \right.$

(5)

用该方程组的最后一个方程减去前n–1个方程即可得方程组如下:

$\left\{ \begin{array}{l} 2({{{x}}_n} - {x_1})x + 2({y_n} - {y_1})y = d_1^2 - d_n^2 - x_1^2+ x_n^2 - y_1^2 + y_n^2 \\ 2({{{x}}_n} - {x_2})x + 2({y_n} - {y_2})y = d_2^2 - d_n^2 - x_2^2+ x_n^2 - y_2^2 + y_n^2 \\ \qquad\qquad\qquad\qquad\qquad\vdots \\ 2({{{x}}_n} - {x_{n - 1}})x + 2({y_n} - {y_{n - 1}})y = d_{n - 1}^2 - d_n^2 - x_{n - 1}^2 + x_n^2\\ \qquad\qquad\qquad\qquad\qquad\qquad - y_{n - 1}^2 + y_n^2 \\ \end{array} \right.$

(6)

然而在实际情况下, 通过测量所得 ${d_1}, {d_2} \cdots {d_i}$ 都是存在误差的, 因此使用最小二乘法去估计待测节点的位置, 则可以得到式(6)的解为:

$X = {({A^{\rm T}}A)^{ - 1}}{A^{\rm T}}B$

(7)

其中, $\hat X = \left[ {\begin{array}{*{20}{l}} {\hat x} \\ {\hat y} \end{array}} \right]$ 为MS的估计位置, 并且:

$A = \left[ {\begin{array}{*{20}{c}} {2({{\rm{x}}_n} - {x_1})}&{2({y_n} - {y_1})} \\ {2({{\rm{x}}_n} - {x_2})}&{2({y_n} - {y_2})} \\ \vdots & \vdots \\ {2({{\rm{x}}_n} - {x_{n - 1}})}&{2({y_n} - {y_{n - 1}})} \end{array}} \right]$

$B = \left[ {\begin{array}{*{20}{c}} {{{\rm{d}}_1}^2 - {d_n}^2 - {x_1}^2 + {x_n}^2 - {y_1}^2 + {y_n}^2} \\ {{d_2}^2 - {d_n}^2 - {x_2}^2 + {x_n}^2 - {y_2}^2 + {y_n}^2} \\ \vdots \\ {{d_{n - 1}}^2 - {d_n}^2 - {x_{n - 1}}^2 + {x_n}^2 - {y_{n - 1}}^2 + {y_n}^2} \end{array}} \right]$

3 基于UKF的环境自适应UWB/DR定位 3.1 选用UKF的合理性分析

线性系统叠加原理表明线性系统的多个输入信号的总响应等于各个信号单独作用产生响应的代数和. 由式(3)可知, DR定位涉及三角函数运算, 因此本文提出的室内定位模型是非线性的, 不符合叠加原理. 一般采用扩展卡尔曼滤波(Extended Kalman Filter, EKF)或无迹卡尔曼滤波处理非线性模型的滤波问题. 其中EKF通过将非线性函数进行Taylor级数展开, 并保留其一阶近似项实现线性化, 难免引入线性化误差, 而UKF利用无迹变换(Unscented Transform, UT)处理均值和协方差的非线性传递问题, 直接基于非线性模型进行解算, 免除线性化误差, 精确度更高^[11-14]. 因此本文选用UKF方法来进行融合滤波.

3.2 UKF预测方程和观测方程确定

根据DR定位建立系统的状态预测方程如下:

${{{X}}_k} = f\left( {{X_{k - 1}}, {\omega _{{R_{k - 1}}}}, {\omega _{{L_{k - 1}}}}} \right) + {Q_k}$

(7)

式中, ${{X}}{\rm{ = }}{\left[ {x, y, \theta } \right]^{\rm T}}$ 为运动状态, $\left( {x, y} \right)$ 为机器人当前位置, $\theta $ 为当前航向, ${\omega _{{R_{k - 1}}}},\;{\omega _{{L_{k - 1}}}}$ 为电机编码器测得的电机转速, 作为运动状态的控制变量, ${Q_k}$ 为三维的过程噪声. 根据式(5)可得 $f\left( {{X_{k - 1}}, {\omega _{{R_{k - 1}}}}, {\omega _{{L_{k - 1}}}}} \right)$ 的表达式为:

$\begin{array}{l} f\left( {{X_{k - 1}}, {\omega _{{R_{k - 1}}}}, {\omega _{{L_{k - 1}}}}} \right) = \\ \left\{ {\begin{array}{*{20}{l}} {{x_{k + 1}} = {x_k} + D\dfrac{{\left( {{\omega _{{L_k}}} + {\omega _{{R_k}}}} \right)}}{2}\left( {{t_{k + 1}} - {t_k}} \right).\sin {\theta _k}} \\ {{y_{k + 1}} = {y_k} + D\dfrac{{\left( {{\omega _{{L_k}}} + {\omega _{{R_k}}}} \right)}}{2}\left( {{t_{k + 1}} - {t_k}} \right).\cos {\theta _k}} \\ {{\theta _{k + 1}}{\rm{ = }}{\theta _k}{\rm{ + }}D\dfrac{{\left( {{\omega _{{L_k}}} - {\omega _{{R_k}}}} \right)}}{L}\left( {{t_{k + 1}} - {t_k}} \right)} \end{array}} \right. \\ \end{array} $

(8)

根据UWB的TOA定位方法可以获得位置坐标, 根据电子罗盘可测得航向, 因此以位置和航向作为观测量从而建立测量方程如下:

${Z_k} = H{X_k}{\rm{ + }}{{\rm{R}}_k}$

(9)

式中, ${R_k}$ 为三维得到观测噪声, H为观测矩阵, 其表达式为:

$H = \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{array}} \right)$

(10)

3.3 UKF方法

无迹卡尔曼滤波的大体思路是结合Kalman线性滤波框架和UT变换来处理均值和协方差的非线性传递问题, 提高非线性问题的滤波效果. UKF计算步骤如下:

(1) 初始化

计算系统状态和方差的初始值, 在导航开始阶段多次采集UWB定位坐标和电子罗盘航向来计算系统状态和方差的初始值.

(2) Sigma点和对应权值计算

$\left\{ \begin{array}{l} {X_0}(k - 1|k - 1) = \overline X (k - 1|k - 1)\\ {X_i}(k - 1|k - 1) = \overline X (k - 1|k - 1) \\ \qquad\qquad\qquad-\sqrt {(n + \lambda )P{{(k - 1|k - 1)}_i}} ,\;\; {i = 1,2 \cdots ,n} \\ {X_i}(k - 1|k - 1) = \overline X (k - 1|k - 1)\\ \qquad\qquad\qquad+\sqrt {(n + \lambda )P{{(k - 1|k - 1)}_i}} ,\\ \qquad\qquad\qquad\qquad{i = n + 1,n + 2 \cdots ,2n} \end{array} \right.$

(11)

$\left\{ \begin{array}{l} \omega _0^{(m)} = \lambda /(n + \lambda )\\ \omega _0^{(c)} = \lambda /(n + \lambda ) + \left( {1 - {\alpha ^2} + \beta } \right)\\ \omega _i^{(m)} = \omega _i^{(c)} = 1/2(n + \lambda ),\left( {i = 1, \cdots ,2n} \right) \end{array} \right.$

(12)

其中, $\lambda = {\alpha ^2}(n + \kappa ) - n$ , $n$ 为系统状态 $X$ 的维数, $\alpha $ 和 $\kappa $ 确定采样点在均值附近的分布, 通常 $\alpha $ 取一个较小的正值, $\kappa {\rm{ = }}3{\rm{ - }}n$ , $P{(k|k)_i}$ 为协方差矩阵的第 $i$ 列. $\beta $ 是非负的权系数, 如果 $x$ 服从高斯分布, $\beta $ 最优值为2.

(3) 状态预测

$\left\{ \begin{array}{l} {X_i}(k|k - 1) = f\left[ {{X_i}(k - 1|k - 1)} \right] \\ \overline X (k|k - 1) = \displaystyle\sum\limits_{i = 0}^{2n} {\omega _i^{(m)}} {X_i}(k|k - 1) \\ P(k|k - 1) = \displaystyle\sum\limits_{i = 0}^{2n} {\omega _i^{(c)}} \left[ {\overline X (k|k - 1) - {X_i}(k|k - 1)} \right] \\ \qquad\qquad\qquad{\left[ {\overline X (k|k - 1) - {X_i}(k|k - 1)} \right]^ {\rm T} } + {Q_k} \\ \end{array} \right.$

(13)

(4) 量测预测

$\left\{ \begin{array}{l} {Z_i}(k|k - 1) = H{X_i}(k|k - 1) \\ \overline Z (k|k - 1) = \displaystyle\sum\limits_{i = 0}^{2n} {\omega _i^{(m)}} {Z_i}(k|k{\rm{ - }}1) \\ {P_{{x_k}{{\textit{z}}_k}}} = \displaystyle\sum\limits_{i = 0}^{2n} {\omega _i^{(c)}} \left[ {{X_i}(k|k - 1) - \overline Z (k|k - 1)} \right] \\ \qquad\qquad{\left[ {{Z_i}(k|k - 1) - \overline Z (k|k - 1)} \right]^{\rm{T}}} \\ {P_{{{\textit{z}}_k}{{\textit{z}}_k}}} = \displaystyle\sum\limits_{i = 0}^{2n} {\omega _i^{(c)}} \left[ {{Z_i}(k|k - 1) - \overline Z (k|k - 1)} \right] \\ \qquad\qquad{\left[ {{Z_i}(k|k - 1) - \overline Z (k|k - 1)} \right]^{\rm{T}}} + {R_k} \\ \end{array} \right.$

(14)

(5) 状态更新

$\left\{ \begin{array}{l} K(k + 1) = {P_{{x_k}{{\textit{z}}_k}}}P_{{{\textit{z}}_k}{{\textit{z}}_k}}^{ - 1}\\ \overline X (k + 1|k + 1) = \overline X (k + 1|k) \\ \qquad+K(k + 1)[Z(k + 1) - \overline Z (k + 1|k)]\\ P(k + 1|k + 1) = P(k + 1|k) \\ \qquad-K(k + 1){P_{{{\textit{z}}_k}{{\textit{z}}_k}}}{K^{\rm T}}(k + 1) \end{array} \right.$

(15)

3.4 环境适应系数构建

由于室内环境复杂, 往往存在着诸多障碍, 采用 UWB进行室内定位时, 其信号传播过程中将会发生反射和折射, 从而导致NLOS误差, 此时LOS状态下确认的UWB定位结果的观测噪声已无法正确反馈. 而利用稳定噪声统计特性的UKF滤波不能得知这种变化, 因而大大影响其滤波的精度和稳定性.为了优化滤波的效果, 构建环境适应系数来对观测噪声实时修正, 使得观测噪声能根据环境变化自适应.

新息定义为:

$\varepsilon (k){\rm{ = }}Z(k) - \overline Z (k|k - 1)$

(16)

理论上, 最优滤波的残差服从均值为零的高斯分布, 其协方差为:

${{D(k) = }}\sum\limits_{i = 0}^{2n} {\omega _i^{(c)}} {\varepsilon _i}(k)\varepsilon _i^{\rm T}(k){\rm{ + }}{R_k}$

(17)

但当BS和MS出现NLOS环境的时候, 残差将会发生显著的变化. 因此可以根据高斯分布的 $3\sigma $ 原则, 利用新息的理论协方差的均方根构建校验信息来对UWB得到的定位结果进行非视距检测.

$\left\{ \begin{array}{l} LOS:\;{\rm{ - }}3\sqrt {{{D(k)}}} \le \varepsilon (k) \le 3\sqrt {{{D(k)}}} \\ NLOS:\;{\rm{ - }}3\sqrt {{{D(k)}}} > \varepsilon (k),\varepsilon (k) > 3\sqrt {{{D(k)}}} \end{array} \right.$

(18)

结合开窗估计法和极大似然估计法可得到新息的实时估计协方差为^[15,16]:

$\widehat {{D}}{{(k) = }}\frac{1}{M}\mathop \sum \limits_{m = 0}^{M - 1} \varepsilon (k{{ - m}}){\varepsilon ^{\rm T}}(k{{ - m}})$

(19)

则利用实时估计协方差和理论协方差构建环境适应系数为:

${\alpha _k} = \left\{ {\begin{array}{*{20}{l}} {I, {\rm LOS}} \\ {\left( {\widehat {{D}}{{(k) - }}\sum\limits_{i = 0}^{2n} {\omega _i^{(c)}} {\varepsilon _i}(k){\varepsilon _i}{{(k)}^{\rm T}}} \right){\rm{/}}{R_{\rm LOS}}, {\rm NLOS}} \end{array}} \right.$

(20)

式中, ${R_{\rm LOS}}$ 为UWB在LOS情况下定位结果的协方差, 则UWB定位的观测噪声在每一次进行无迹卡尔曼滤波的时候都进行动态修正为:

${R_k} = {\alpha _k}{R_{\rm LOS}}$

(21)

4 实验分析

实验环境如图5所示, 在场地内共放置了4个UWB基站, 坐标分别为A(0, 0), B(840, 0), C(0, 840), D(840, 840), 单位为cm. 数据采集移动平台在移动过程中的可以实时采集航向和车速信息, 并通过ESP8266不断向外传输, UWB基站A通过串口不断向外发送移动站和各个基站的距离. 通过自主开发的C#软件同频率实时记录以上数据.

为了更好验证所提出方法的定位效果, 设计途经NLOS误差路段的折线路径实验, 即采集平台在空间阻挡的区域中按计划路径匀速运行时的信息. 由于NLOS误差的存在, 观测噪声模型必然呈现非高斯特性. 至此可知, 室内定位模型是非线性且非高斯的. 而粒子滤波是一种适于处理此类模型的成熟滤波方法. 因此本文分别通过UKF、PF和环境自适应UKF方法处理数据, 并比对和分析定位效果得出实验结果.

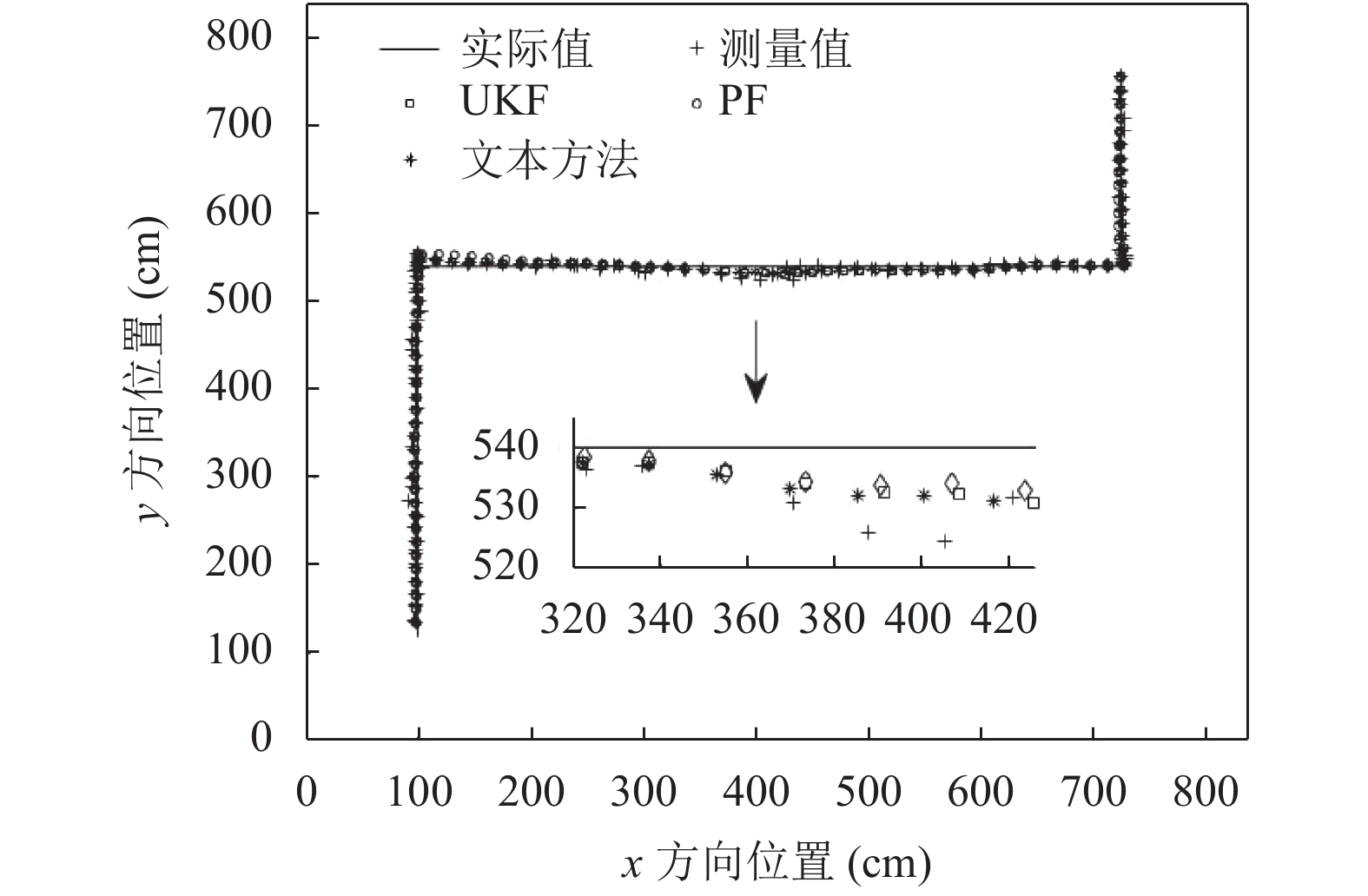
实验结果如图6~图9所示, 分别分析基于最小二乘法得到的测量值、UKF方法、PF方法以及本文方法的运动轨迹复现、定位误差、定位累计误差以及定位误差累积概率分布.

图6对比了不同方法的运动轨迹复现结果, 可以看出, 在LOS情况下测量值也有着较高的定位精度, 此时基于非视距检测构建的环境适应系数为I, 即环境自适应UKF和UKF具有相同滤波效果; 当存在NLOS测距异常值时, 测量值的定位精度明显降低, UKF、PF和环境自适应UKF方法均表现出较强的抗NLOS性能.

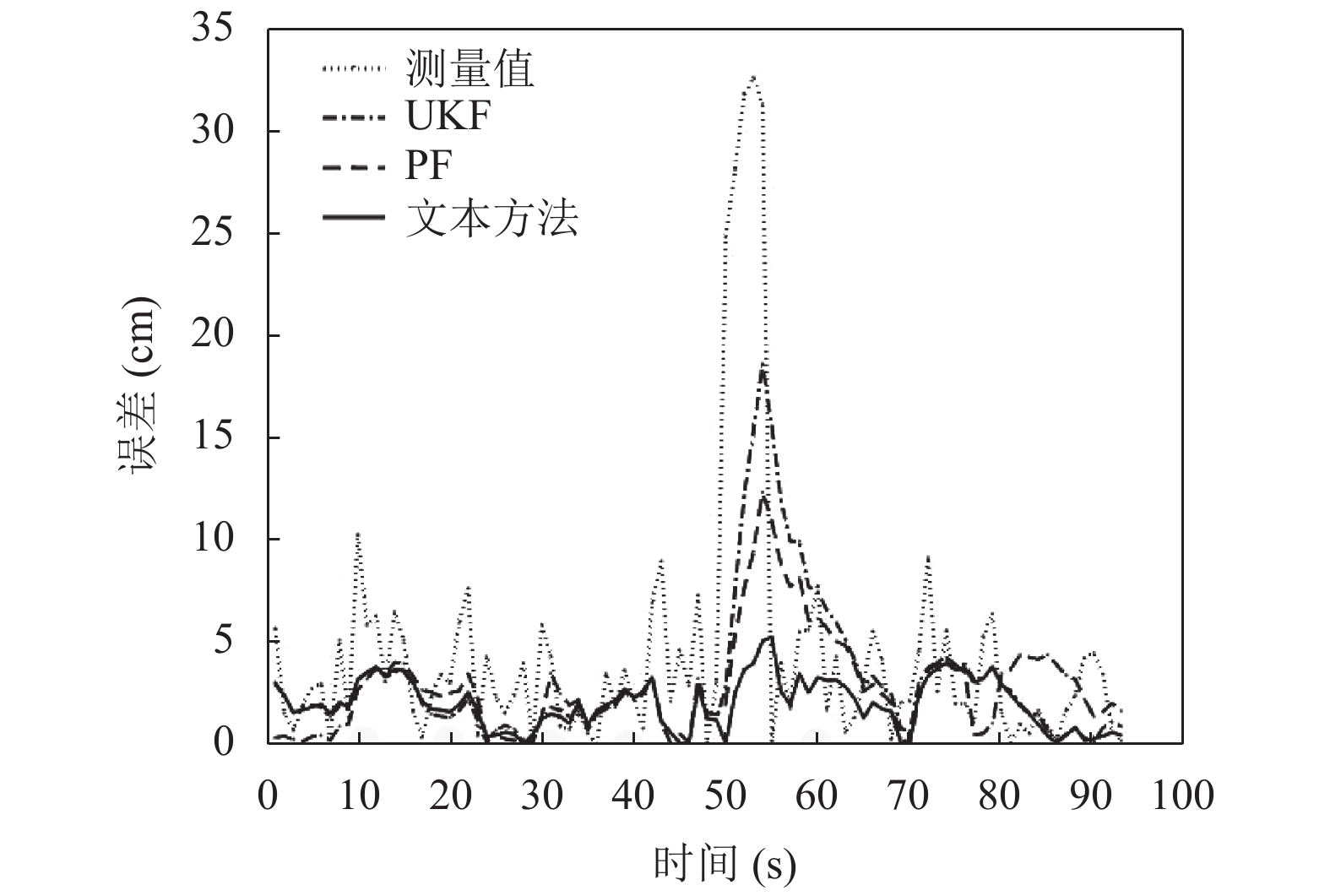
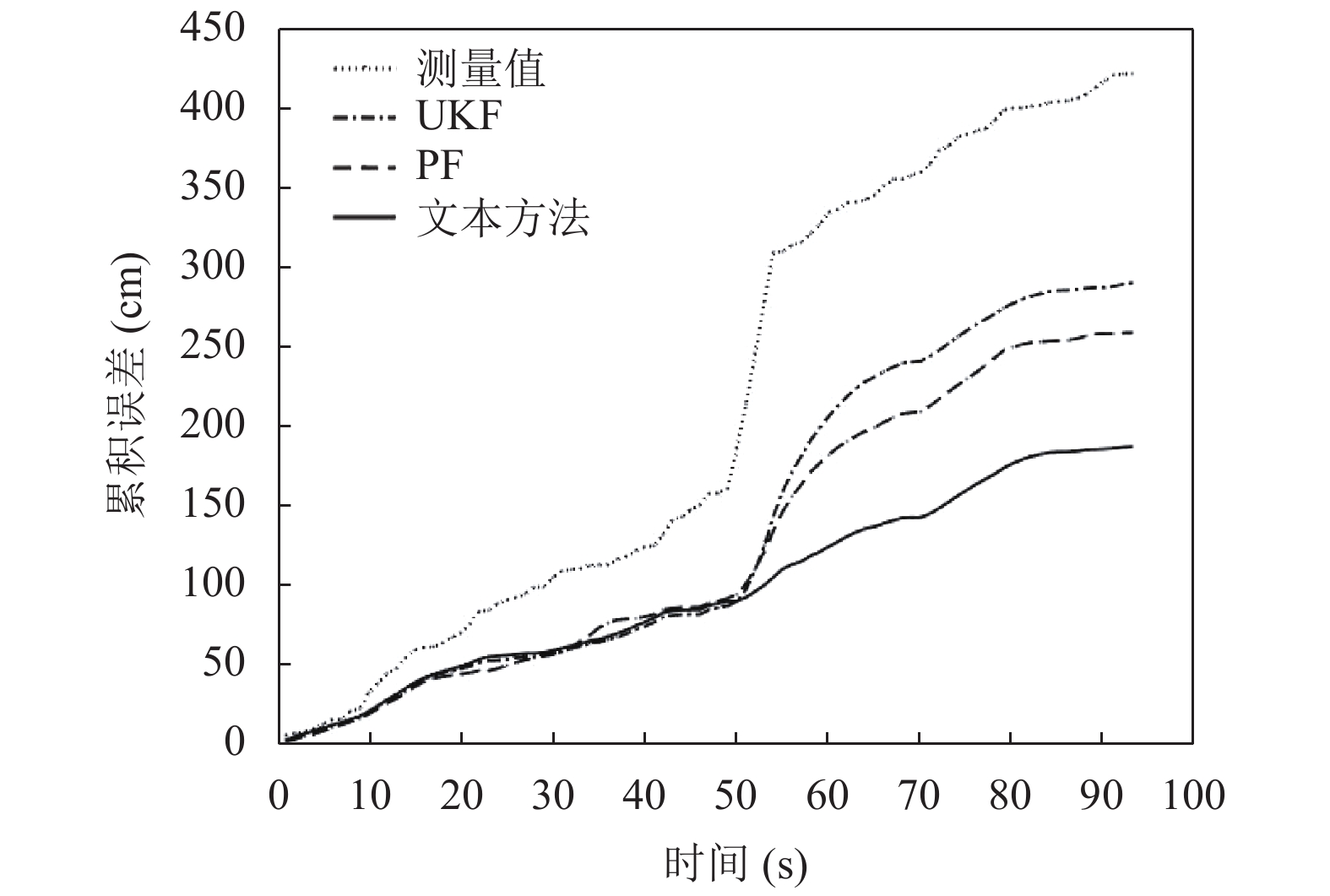
图7和图8中50~60 s可以看出, 当出现NLOS误差的时候, 测量值的定位误差明显增大, UKF方法和PF方法一定程度抑制了误差, 本文方法能够显著提高NLOS情况下的定位精度, 使之与LOS情况下的定位误差变化与累计误差增长趋势相近.

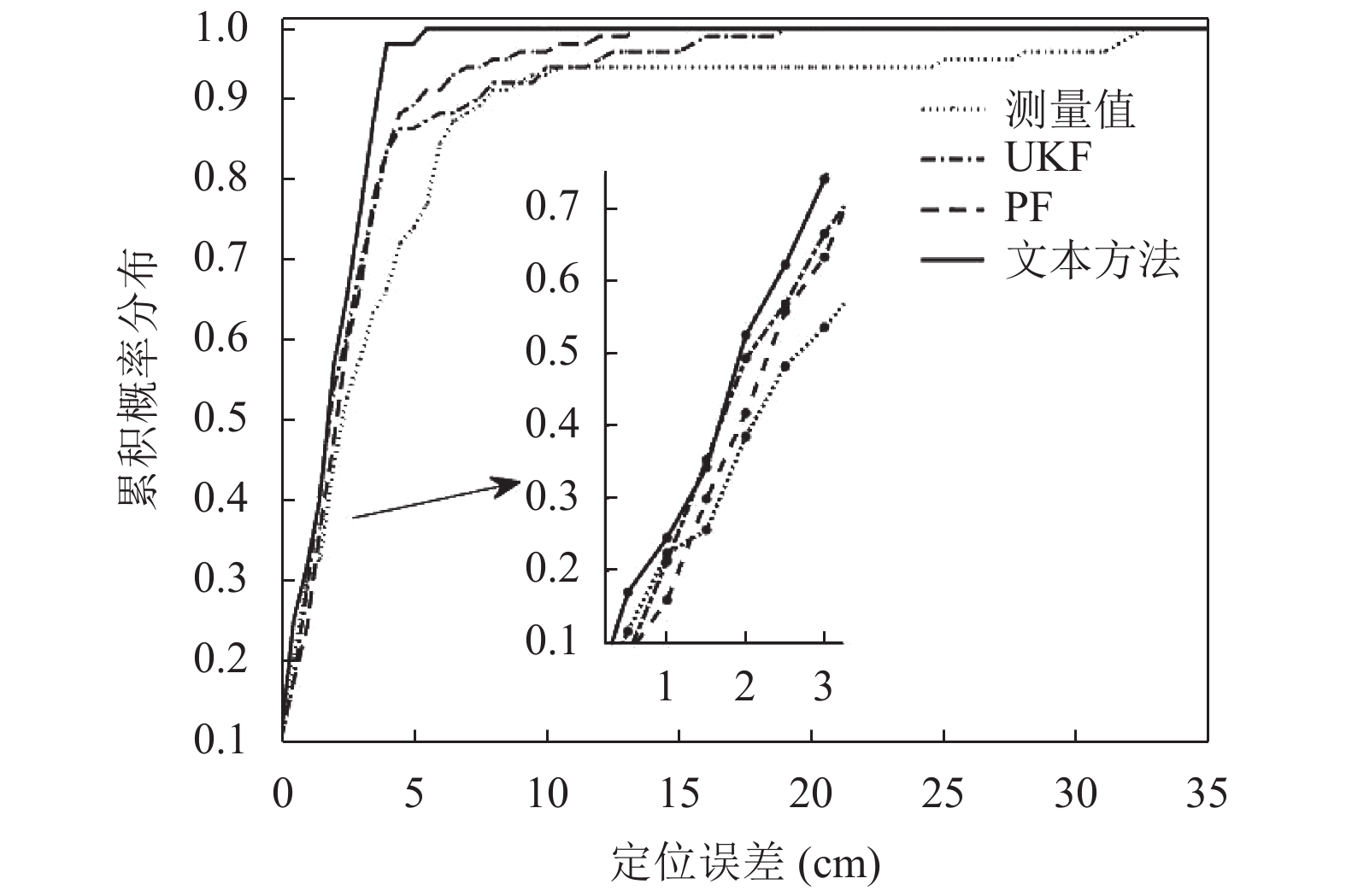
图9所示为不同方法的误差累积概率分布, 进一步验证了在有遮挡的路径下, 本文方法相比于其它方法具有更优的定位性能.

表1是NLOS误差量化表,从中可以看出在NLOS情况下, 本文方法的最大误差值、平均误差值相较其他方法最低, NLOS降低率最高. 此外用Matlab统计得, UKF、PF、本文方法的运算时间分别是0.0117 s, 0.6094 s, 0.0125 s. 因此PF方法定位效果略优于UKF方法, 但运算效率过低; 环境自适应UKF通过消耗低成本运算效率换得显著优于UKF方法的定位效果, 进一步表明在NLOS情况下, 本文方法相比于其它方法具有更好的性能.

总之, 实验数据和结果表明, 本文方法在LOS情况下定位效果与UKF方法、PF方法相近; 在NLOS情况下, 由于环境适应系数的动态修正, 比UKF方法和PF方法具有更高的定位性能.

5 结论

针对复杂室内环境下UWB信号传播的非视距NLOS误差问题, 本文提出基于UKF的环境自适应UWB/DR室内定位方法. 该方法从UWB定位环境的误差产生原因出发, 通过建立环境自适应UKF滤波模型, 在UWB/DR定位融合过程中对UWB定位信息进行非视距检测并且引入环境适应系数动态修正UWB定位观测噪声. 实验效果表明, 该方法具有较高的抗NLOS误差性能, 定位精度优于PF方法和UKF方法, 是一种具有较强实用性且高精度的室内定位方法.