近年来, 康复医学取得了突破性进展, 脑功能的康复理论与实践研究证明, 通过康复治疗可以观察到中枢神经系统的变化, 中枢神经系统残留部分具有很大的代偿能力. 通过运动训练, 可以恢复其功能[1]. 脑卒中是一种以脑部缺血及出血性损伤为主要症状为临床表现的疾病, 又称中风, 具有发病率高、致残率高、死亡率高和复发率高的特点[2]. 《2018中国卫生健康统计提要》中数据显示2017年脑血管病是我国成年人致死、致残的首位病因[3]. 脑卒中患者要尽早采取康复训练. 早期康复训练治疗在减轻脑卒中造成的运动功能障碍, 提高生活质量有着关键性的作用. 卒中后越早开始使用机械装置进行康复训练, 患者的运动恢复率越高[4]. 除了脑卒中(cerebral stroke)之外, 脊髓损伤、下肢退行性关节等由于神经系统导致肢体功能障碍的疾病, 急需得到大量的高强度的、有针对性和重复性的康复训练, 而目前主要依赖于治疗师一对一训练, 对训练师来说劳动强度大, 康复训练时间长且频率高, 难以保证训练的持续性和稳定性, 治疗效果还受到康复训练治疗师水平影响[5]. 需要合格的下肢康复医疗设备对各种神经功能障碍的患者进行步态康复训练. 发达国家对下肢康复机器人的研究较早, 已经从单纯的实验室样机研究发展到市场化产品阶段, 如Ekso、Lokomat[6]、HAL[7]等. 例如日本筑波大学研发下肢外骨骼机器人HAL, 通过监测大脑传递给肌肉的电信号, 从而预见和支持人体的行动, 但是国外产品存在价格昂贵、体积较大等问题. 如瑞士的Erigo重量达300 kg, Lokomat更是超过了800 kg. 同时价格十分昂贵, 如Erigo售价约160万元人民币, Lokomat约300万, 超过了大部分患者的负担能力. 而国内的康复机器人大多处于实验室阶段或处于上市前的临床测试阶段, 与国外差距较大[8]. 针对以上问题, 本文在满足大量、合格的重复性训练的前提下设计了一款新型的轮椅式下肢康复机器人, 相比于国内外的产品具有以下4个优点:
(1) 可以切换坐、立、躺3种模式, 同时价格较低;
(2) 底部为轮式结构,增加轮毂电机, 具有移动能力,可解决因体积巨大无法移动的问题, 携带了大容量的锂电池,可在室内外进行较长时间的训练;
(3) 设计了人机交互平台, 搭载了工控机Windows平台,设计了一种远程的医疗监控系统, 相比于国外复杂的英文操作界面更加符合国人的需求;
(4) 研究了康复机器人在站立情况下进行步态训练时与移动车体电机的速度协调控制, 使患者在训练时机器人车体可以同步移动.
1 康复机器人总体设计方案轮椅式下肢康复机器人主要由移动车体框架、支撑与升降机构、姿态转换模块、外骨骼机械腿、终端控制系统5部分组成. 轮椅式下肢康复机器人验机如图1所示. 下面将就这5部分进行简单的介绍.
1.1 移动车体框架为了让患者可以在室内外使用该康复机器人进行日常康复训练和方便生活出行, 设计了移动车体框架, 出于稳定性考虑选择两轮驱动机构, 该部分主要由2个无刷电机和2个带有弹簧减震的万向轮组成, 配套了ZLAC706轮毂伺服驱动器和操作摇杆, 由前轮驱动带动后轮从而带动车辆前进, 通过两轮驱动轮的速度差来实现对整个车体转向控制, 采用PID算法, 优化了在平地上人体下肢运动和小车移动间的协调算法, 使两者速度匹配.实现边训练小车边移动的效果.
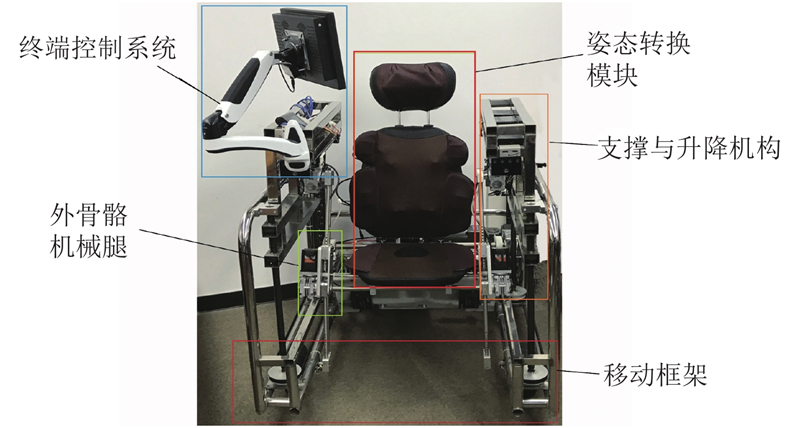
|
图 1 轮椅式康复机器人整体图 |
1.2 支撑与升降机构
康复机器人利用300 W的直流电机转动时连接皮带传送带动丝杆转动, 从而控制机械腿机构的上升下降. 如图2和图3所示, 通过该机构配合机械腿, 先将机械腿移动到座椅前的5 cm距离, 通过绑带将下肢固定在机械腿上, 再通过升降机构, 同时需要患者双手支撑把手, 配合升降机构的上升过程, 于此同时步进电机驱动丝杆滑块将座椅收回去, 防止座椅干涉患者站姿下的步行训练. 姿态转换和升降机构合理配合, 将可以提供患者站立过程中的动力或提供坐下过程的支撑缓冲, 同时保持身体重心的垂直和横向运动, 帮助患者完成起坐动作.

|
图 2 康复机器人坐姿图 |

|
图 3 患者切换站立训练图 |
1.3 姿态转换模块
姿态转换模块即用户可选择站、坐、卧3种姿态进行康复训练, 符合不同阶段用户的肢体躯干承受能力, 以此来满足不同阶段患者用户的康复训练要求. 在下肢行动障碍患者早期的治疗过程中, 由于患者肢体力量基本丧失, 肢体肌肉力量无法支撑其站立运动, 故设计了该姿态转换模块, 患者可实时调整姿态, 使自己处于坐姿、斜躺、平躺、站立姿势下进行腿部的康复训练, 进行肌肉刺激训练, 等到部分恢复其下肢运动功能后再进行站立姿态下的步行训练. 图4是康复机器人坐姿转换为斜躺姿态三维图.
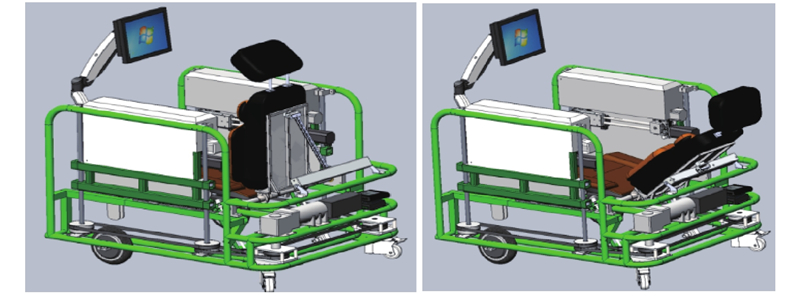
|
图 4 康复机器人坐姿转换为斜躺姿态三维图 |
1.4 外骨骼机械腿
外骨骼机械腿是整个康复机器人的核心部分, 本文研究的多功能轮椅式下肢康复机器人主要研究的是髋关节、膝关节、踝关节的屈伸运动, 主要考虑在矢状面内的运动而不考虑其他平面的运动. 机械外骨骼左右腿对称, 机构上有滑块和螺纹孔, 可以根据患者的实际身高进行调节. 根据《GB10000-1988中国成年人人体尺寸标准》[9], 选取结构的长度, 其中大腿杆的长度范围为400 mm~505 mm, 小腿杆的长度范围为310 mm~410 mm. 关节处的电机选用伺服电机, 转矩为1.89 N·m, 减速器为RV减速器, 髋关节电机处减速比1:40, 膝关节电机处减速比1:20, 根据临床步态分析数据库(Clinical Gait Analysis, CGA)数据可知人正常行走时髋关节的力矩最大值为50 N·m, 髋关节的力矩最大值为40 N·m. 电机力矩符合要求. 可以根据采集到的人体步态数据去规划康复运动的轨迹, 控制机械腿上的伺服电机完成机械腿的步态运动算法和协调控制. 图5是康复机器人助行腿及其运动学模型.
1.5 终端控制系统康复机器人的控制系统是在工控机Windows平台中开发的, 上位机采用Delphi、C#开发, 下位机采用STM32f103zet6单片机, 采集各类传感器感知数据, 采用角度传感器采集机械腿转动角度, 超声波传感器检测碰撞安全距离, 光电限位开关检测升降机构, 座椅机构, 机械腿进退等极限位置安全距离, 搭建了小型远程医疗系统平台, 搭建了服务器, 开发了安卓APP, 主治医生可实时检测患者的康复训练情况. 图6是康复机器人操作界面.

|
图 6 康复机器人操作界面 |
2 康复机器人与移动车体协调控制算法 2.1 患者被动训练模式下的协调控制
患者的被动训练模式, 是指其在早期的是指患者在早期的康复训练中, 下肢肢疲软, 肌肉力量不足, 患者没有肌肉力量去步行, 只能由机器提供动力带动腿部进行康复训练. 如果想要达到良好的康复效果, 机械外骨骼必须提供稳定可靠的动力, 再按照规划好的步态轨迹进行康复训练, 让患者的双腿往复运动达到理想的康复效果. 人步态训练过程中分为支撑期和摆动期. 支撑相是在步行中足与地面始终有接触的阶段, 患者的训练过程中, 抬腿时, 足跟先离地再到足尖离地, 这一过程中有一个瞬间的速度, 患者脚尖离地的速度与车体的速度一致才能使脚尖与地面顺利分离, 避免脚踝受伤甚至绊倒. 同样的, 落地时, 是脚跟先落地再到全足底落地, 这个过程也需要保证患者脚底的速度和机器人移动车体的速度一致才能让患者与车体保持动作一致, 达到良好的康复效果.
因此, 在康复训练的时候, 为了达到患者和康复机器人的同步移动, 需要进行以下的几个步骤:
(1) 采集正常的人体步态数据, 建立步态数据库, 作为患者康复步态的轨迹轨迹划依据.
(2) 将采集的步态数据进行处理, 用Matlab进行拟合, 建立髋关节和膝关节的数学模型, 研究拟合函数中各个参数与步速之间的关系, 从而建立步速跟随型的各关节运动模型, 并依据此模型对康复机器人的各个关节进行控制. 将其作为髋关节、膝关节电机控制的轨迹规划依据. Matlab的CFTOOL工具箱使用方便, 可以实现多种类型的线性非线性的曲线拟合, 将其作为本次数据的拟合工具. 傅利叶分析理论已非常成熟, 已成为周期信号处理的基本工具. 广泛用于连续周期信号的分析和处理[10], Fourier函数拟合拟合效率相对较高, 一般能很好的拟合多峰值、有明显周期特性和曲线性的实验数据, 因而本次采用Fourier函数拟合步态数据. 傅利叶级数为:
| $ f(t) = {a_0} + \displaystyle\sum\limits_{n = 1}^\infty {\left[ {\left( {{a_n}\cos \left( {n{\omega _T}t} \right) + {b_n}\sin \left( {n{\omega _T}t} \right)} \right)} \right]} $ | (1) |
若
(3) 已经确定了各个关节的运动模型之后, 就要进行患者的实际康复训练过程.
在步长不变的情况下, 改变步频并不改变髋膝关节角度的大小, 只改变数据点之间的时间间隔[11].
在患者被动训练模式下, 康复医师先通过机器人的终端操作软件设置康复机器人车体的速度VC, VC有快速慢速中速三种模式, 假定中速的车体速度为1 km/h, 根据中国成年男子一般步长数据, 约50~80 cm, 配合康复医疗师前期采集到的患者步长LS, 则能计算出整个步态的周期TS为:
| $ {T_S} = \frac{{2 \cdot 3.16 \cdot {L_S}}}{{{V_C}}} = \frac{{7.2{L_S}}}{{{V_C}}} $ | (2) |
当训练步长LS确定后,由
(4) 根据步态运动的周期, 计算出下肢矫形器各个关节的角频率
由前面分析可知, 按训练步长确定的各关节角变化轨迹的周期仍是基础步态的周期
| $ {\theta _H}(t) = {a_{10}} + \sum\nolimits_{n = 1}^3 {\left[ {\left( {{a_{1n}}\cos \left( {n{\omega _T}t} \right) + {b_{1n}}\sin \left( {n{\omega _T}t} \right)} \right)} \right]} $ | (3) |
| ${\theta _k}(t) = {a_{20}} + \sum\nolimits_{n = 1}^5 {\left[ {\left( {{a_{2n}}\cos \left( {n{\omega _T}t} \right) + {b_{2n}}\sin \left( {n{\omega _T}t} \right)} \right)} \right]} $ | (4) |
式中,
根据髋关节与膝关节的角位移, 获得在整个步态运动周期TS内髋关节与膝关节的运动轨迹; 使得下肢外骨骼机械腿满足式(3)和式(4)中计算出的运动轨迹, 则能在周期TS内, 下肢外骨骼的运动速度与移动车体同步. 同时, 则需要让脚跟触地到脚尖触地的时间内的计算出人体前进的位移.
由
将下肢外骨骼某支腿底中心记为A点, 脚底中心A在基坐标0下的x方向位置记为
在t1时刻, 即用户脚尖开始与地面刚开始接触的时刻, 髋关节与膝关节对应的角位置分别为
| $ {P_{A1}} = {I_1} \cdot \sin {\theta _{H1}} + {L_2} \cdot \sin \left( {{\theta _{H1}} - {\theta _{K1}}} \right) $ | (5) |
求得t1时刻机器人车体位移B点的位置
| $ {P_{A1}}={P_{B1}} $ | (6) |
在t2时刻, 已知车体移动速度为
| ${P_{A2}} = {L_1} \cdot \sin {\theta _{H1}} + {L_2} \cdot \sin \left( {{\theta _{H2}} - {\theta _{K2}}} \right) $ | (7) |
令
| $ \begin{split} &{L_1} \cdot \sin {\theta _{{H2}}} + {L_2} \cdot \sin \left( {{\theta _{H2}} - {\theta _{K2}}} \right) = \\ &\quad{L_1} \cdot \sin {\theta _{H1}} + {L_2} \cdot \sin \left( {{\theta _{H1}} - {\theta _{K1}}} \right) + {V_C} \cdot \left( {{t_2} - {t_1}} \right) \end{split} $ | (8) |
即可保证机器人助行腿在离地瞬间和机器人移动车体速度同步. 但是在实际使用中发现这种方法会有偏差, 而导致
| $ \omega = {\omega _T}/{k_p} $ | (9) |
单位是rad/s, 则:
若
若
改写式(3)、式(4), 设置
| ${\theta _H}(t) = {a_{10}} + \sum\nolimits_{n = 1}^3 {\left[ {\left( {{a_{1n}}\cos \left( {\frac{{n{\omega _T}t}}{{{K_p}}}} \right) + {b_{1n}}\sin \left( {\frac{{n{\omega _T}t}}{{{K_p}}}} \right)} \right)} \right]} $ | (10) |
| $ {\theta _k}(t) = {a_{20}} + \sum\nolimits_{n = 1}^5 {\left[ {\left( {{a_{2n}}\cos \left( {\frac{{n{\omega _T}t}}{{{K_p}}}} \right) + {b_{2n}}\sin \left( {\frac{{n{\omega _T}t}}{{{K_p}}}} \right)} \right)} \right]} $ | (11) |
重复式(5)至式(11)直至
患者主动模式下的康复训练, 即助行腿不主动提供动力, 而是由患者自主运动. 这是在患者的健康状况有所恢复之后, 下肢功能有所恢复, 在医生的允许下, 不依靠外力去尝试主动行走.

|
图 7 患者被动训练模式下协调控制流程图 |
这种情况相对于被动行走在控制上会容易实现, 因为不需要实时去调整各个关节的运动速度. 患者的主动运动, 是通过安装在大腿中部和小腿中部的两个拉压传感器感知患者运动意图(如图8), 当患者抬腿时拉压传感器压力减小, 电机驱动下肢抬起, 当采集到的压力增大表明患者正向后收缩, 关机电机反方向运动.

|
图 8 康复下肢机械腿意图检测装置 |
感知到患者的运动意图之后, 髋关节和膝关节的伺服电机开始运动, 运动的速度、启停等由患者主动控制, 再通过单位时间内髋关节膝关节的角度变化换算成位移的差值, 由上位机计算出速度发送给机器人车体的轮毂电机, 从而做到协调控制. 图9是人体步态周期图, 图10是患者步行训练运动过程.

|
图 9 人体步态周期图 |

|
图 10 患者步行训练运动过程 |
忽略脚踝及其以下部分的运动, 本文提出的康复机器人的康复训练只在矢状面内进行, 并不涉及其他面的运动. 人体的步态周期过程如图11所示, 康复机器人助行腿简化为5连杆机构, 并将整个整个步态周期划分为5个部分: 双足支撑→右腿支撑, 左腿迈步→双足支撑→左腿支撑, 右腿迈步→双足支撑[13], 可以简化对应成图11的运动过程, 以此建立患者康复训练的运动模型, L1表示左腿, L2表示右腿,
| $\begin{split} x\left[ {{\varphi _h}(t),{\varphi _k}(t),{\varphi _a}(t)} \right] & ={I_1}\sin \left[ {{\varphi _h}(t)} \right] + {I_2}\sin \left[ {{\varphi _h}(t) + {\varphi _k}(t)} \right]\\ &\quad + {L_3}\sin \left[ {{\varphi _h}(t) + {\varphi _k}(t) + {\varphi _a}(t)} \right] \end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ | (12) |
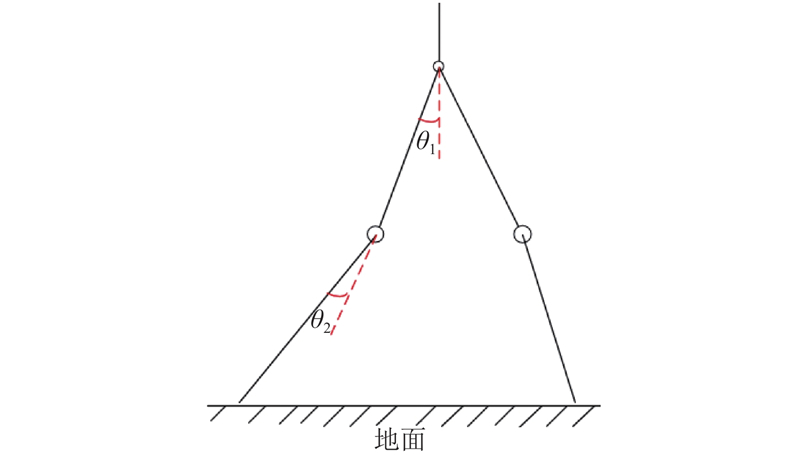
|
图 11 双足支撑示意图 |
由于不涉及踝关节的电机控制, 又可以简化为:
| $ x\left[ {{\varphi _h}(t),{\varphi _k}(t)} \right] = {I_1}\sin \left[ {{\varphi _h}(t)} \right] + {I_2}\sin \left[ {{\varphi _h}(t) + {\varphi _k}(t)} \right] $ | (13) |
对上式求导, 可以求出理想患者的脚的速度V, 如式(13)所示.
| $V = \frac{d}{{dx}}x\left( {{\varphi _h}(t),{\varphi _k}(t)} \right) $ | (14) |
上述分析已经得到了患者下肢训练速度的数学表达式(14), 接下来要将在其工程中具体实现出来.
如图5所示, 由于康复机构的下肢机械腿设计成髋关节的连接处和移动车体相连接, 患者的步行训练过程实际上可以看成髋关节位移与车体的移动速度相匹配, 否则会阻碍患者的康复训练效果, 现将训练的过程划分为如下的几个过程:

|
图 5 康复机器人助行腿及其运动学模型 |
初始状态是先让患者直立, 用AD采集卡读取此刻角度传感器的读数, 接下来髋、膝关节的角度变化值只需要计算差值即可.
(1) 患者从双足支撑到右腿支撑左腿迈步的过程中, 此时脚底压力传感器双腿读数相差不大, 此时
| $ X = {L_1} \cdot \sin {\theta _1} + {L_2} \cdot \sin \left( {{\theta _1} - {\theta _2}} \right) $ | (15) |
(2) 右腿支撑左腿迈步到双足支撑过程中, 仍然只需要采集右腿角度传感器的角度变化值即可求得位移的变化, 此时
| $ X = {L_1} \cdot \sin (-{\theta _1}) + {L_2} \cdot \sin \left( -{{\theta _1} - {\theta _2}} \right) $ | (16) |
(3) 双足支撑到左腿支撑过程中, 只需要采集左腿角度传感器的角度变化值即可求得位移的变化.
(4) 此时
| $X = {L_1} \cdot \sin {\theta _3} + {L_2} \cdot \sin \left( {{\theta _3} - {\theta _4}} \right) $ | (17) |
(5) 左腿支撑右腿迈步到双足支撑过程中, 仍然只需要采集左腿角度传感器的角度变化值即可求得位移的变化, 此时
| $ X = {L_1} \cdot \sin \left( { - {\theta _3}} \right) + {L_2} \cdot \sin \left( { - {\theta _3} - {\theta _4}} \right) $ | (18) |
至此, 患者步行训练的一个步态周期完成, 继续下一个步态周期. 算法的关键点在于步态时刻的划分, 由足底的薄膜压力传感器鞋垫测得, 如图12.

|
图 12 薄膜压力传感器内嵌入鞋子 |
再由
基于上述算法, 搭建了康复机器人步态数据采样平台, 将角度传感器绑在人体腿上, 采集多组数据建立人体步态数据库, 作为患者的步态规划依据, 如图13所示. 采样软件为Delphi开发, 如图14所示.
采集到的曲线如图14所示. 将采集过程中的关节角度信息保存在txt中, 取一个完整的步态周期的数据, 用Matlab的CFTOOL工具箱(如图15)进行Fourier函数拟合, 发现髋关节3阶Fourier拟合效果最好(如图16), 膝关节5阶Fourier拟合效果最好(如图17).
髋关节的拟合函数为:
| $ \begin{split} {f(x) = {a_0} + {a_1}\cos (x \cdot \omega ) + {b_1}\sin (x \cdot \omega ) }\\ \;\;\;\;\;\;\;\;\;\;\;+{{a_2}\cos (2 \cdot x \cdot \omega ) + {b_2}\sin (2 \cdot x \cdot \omega ) }\\ \;\;\;\;\;\;\;\;\;\;\;+{{a_3}\cos (3 \cdot x \cdot \omega ) + {b_3}\sin (3 \cdot x \cdot \omega )} \end{split} $ | (19) |
其中, a0=28.04, a1=20.33, b1=–7.278,a2=5.186, b2=1.583, a3=–0.1338,b3=2.202, ω=0.05884.
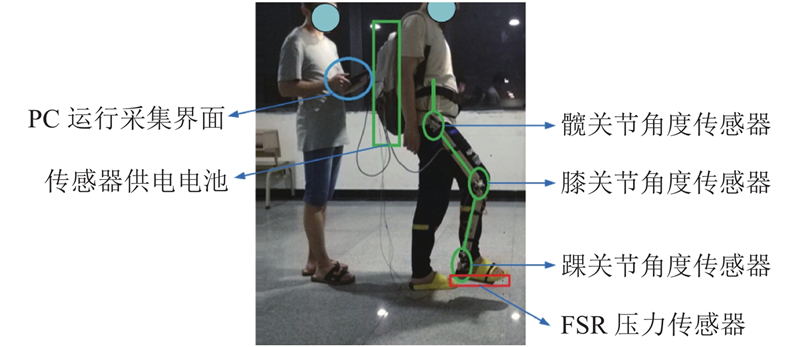
|
图 13 数据采集现场图 |

|
图 14 步态数据采集软件界面 |

|
图 15 CFTOOL工具箱使用界面 |

|
图 16 髋关角度节拟合曲线 |

|
图 17 膝关节角度拟合曲线 |
膝关节采用5阶Fourier拟合, 拟合函数为:
| $ \begin{split} f(x) = {a_0} + {a_1}\cos (x \cdot \omega ) + {b_1}\sin (x \cdot \omega ) \\ \;\;\;\;\;\;\;\;\;\;\;+ {a_2}\cos (2 \cdot x \cdot \omega ) + {b_2}\sin (2 \cdot x \cdot \omega ) \\ \;\;\;\;\;\;\;\;\;\;\;+{a_3}\cos \left( {3 \cdot x \cdot \omega + {b_3}\sin (3 \cdot x \cdot \omega ) } \right.\\ \;\;\;\;\;\;\;\;\;\;\;+{a_4}\cos (4 \cdot x \cdot \omega ) + {b_4}\sin (4 \cdot x \cdot \omega ) \\ \;\;\;\;\;\;\;\;\;\;\;+{a_5}\cos (5 \cdot x \cdot \omega ) + {b_5}\sin (5 \cdot x \cdot \omega ) \end{split} $ | (20) |
其中, a0=–34.550, a1=–0.9422, b1=20.550, a2=15.310, b2=–4.366, a3=3.391, b3=–4.234, a4=0.8265, b4= –0.8364, a5=1.097, b4=–3.391, ω=0.063.
由以上拟合结果为依据, 建立康复机器人各关节运动的数学模型, 作为控制依据.
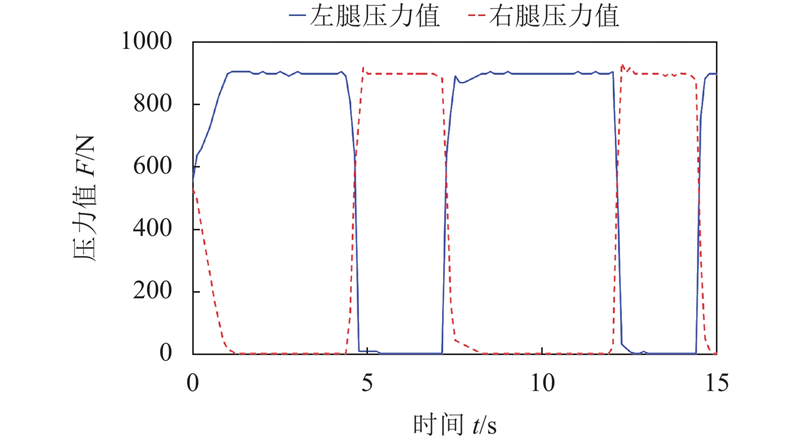
3.2 患者主动模式下协调控制的实验如图18所示, 采用FSR402薄膜压力传感器, 采集卡为阿尔泰USB2832采集卡采集电压转换模块上的电压换算成压力值, 压力值记录在txt文件中, 用Matlab低通滤波, 表明FSR的到达阈值后的波动基本平稳, 可以判断足底的落地时刻, 符合步行实验的步态相位划分要求.
|
图 18 FSR传感器数据采集 |
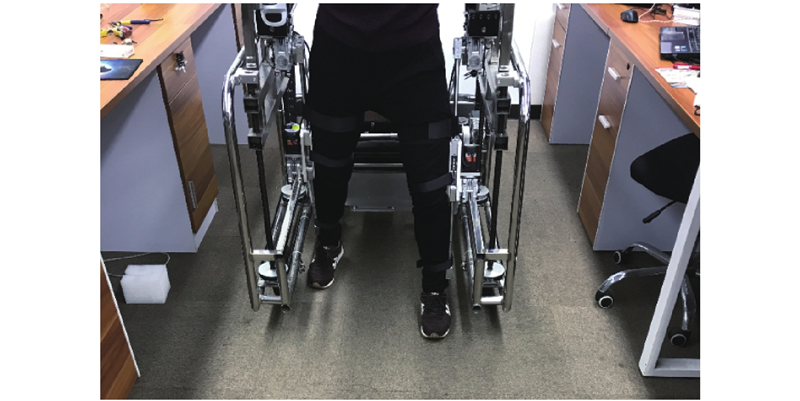
图19是患者主动模式下步态训练. 本次的实验对象为身高175 cm, 体重65 kg的正常成年男性, 训练过程中髋关节和膝关节机构制做了特殊的同步传送带轮机构, 同时用3D打印机打印了特殊的支架装置固定角度传感器(如图20和图21), 可实时通过AD采集卡采集关节的角度, 不断的计算发送给轮毂电机.
|
图 19 患者主动模式下步态训练 |
图22为康复机器人控制软件界面及各关节角度控制数据曲线图, 图中髋、膝、踝关节的角度值与采集到的标准数据基本一致, 表明通过患者主动在控制自己进行训练, 速度有快有慢, 通过计算, 可以得出当前时刻北京时间20:50:08:116的实时速度为0.813 m/s, 将其发送给车体. 如图23所示, 工控机通过轮毂电机控制软件, 通过串口发送给轮毂电机当前需要运动的速度, 轮毂电机经过PID算法调试能快速响应, 在10 ms内到达指定的速度, 系统的协调控制性能良好.

|
图 20 特殊角度检测装置三维图 |

|
图 21 特殊角度检测装置实物图 |

|
图 22 康复机器人速度协调控制软件 |

|
图 23 轮毂电机实时速度曲线图 |
选取了6位志愿者进行患者主动模式下的康复训练实验,限制移动车体的速度为1 m/s, 实验结果汇总为表1, 可以看出,移动车体的速度和受试者的速度基本一致,误差在很小的范围内,同时可以看出3号受试者的速度大于1 m/s的时候,车体速度 限制为1 m/s, 可以保证患者用户的安全. 实验结果表明, 下肢外骨骼行走的速度曲线和轮椅式车体的速度曲线基本一致, 可实现患者和康复机器人移动车体的协调控制.
| 表 1 患者主动模式下协调控制实验结果 |
4 结论与展望
通过以上理论分析及实验可发现, 通过角度、拉压、FSR足底压力等传感器配合康复机器人搭载的工控机平台计算可实时获取患者训练的步行速度, 以此发送给机器人移动车体的轮毂电机, 可以完成机器人的可协调性设计. 同时这种训练方式可以让患者能在室外实地步行, 呼吸自然空气, 对患者的心理也有很好的舒缓作用. 相比于跑步机形式的固定康复机器人具有更好的康复效果和更好的推广价值和研究意义.
| [1] |
蒋戈利. 康复医学发展趋势及设想. 解放军医药杂志, 2013, 25(1): 1-5. DOI:10.3969/j.issn.2095-140X.2013.01.001 |
| [2] |
黄敏, 蔡丽琼, 孙荣. 延续性护理模式对脑卒中患者出院后的影响. 实用临床医药杂志, 2016, 20(10): 154-155. |
| [3] |
王陇德, 刘建民, 杨弋, 等. 我国脑卒中防治仍面临巨大挑战——《中国脑卒中防治报告2018》概要. 中国循环杂志, 2019, 34(2): 105-119. |
| [4] |
周莉, 李江东, 刘景隆. 脑卒中患者开始康复时间和康复持续时间与运动功能的恢复. 中国临床康复, 2005, 9(17): 1-3. |
| [5] |
林惠. 下肢康复机器人训练与评估系统的应用. 中国康复医学会疗养康复专业委员会第二十四届学术会议论文集. 广州. 2014. 205–206.
|
| [6] |
Mirbagheri MM, Niu X, Kindig M, et al. The effects of locomotor training with a robotic-gait orthosis (Lokomat) on neuromuscular properties in persons with chronic SCI. Proceedings of 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. San Diego, CA, USA. 2012. 3854–3857.
|
| [7] |
Tsukahara A, Hasegawa Y, Eguchi K, et al. Restoration of gait for spinal cord injury patients using HAL with intention estimator for preferable swing speed. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2015, 23(2): 308-318. DOI:10.1109/TNSRE.2014.2364618 |
| [8] |
Talaty M, Esquenazi A, Briceño JE. Differentiating ability in users of the ReWalkTM powered exoskeleton: an analysis of walking kinematics. 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR). Seattle, WA, USA. 2013. 6650469.
|
| [9] |
国家技术监督局. GB10000–1988 中国成年人人体尺寸[S]. 北京: 中国标准出版社, 1989.
|
| [10] |
何卫华. 运用下肢关节角度信息的步态识别[硕士学位论文]. 重庆: 重庆大学, 2007.
|
| [11] |
程方, 王人成, 贾晓红, 等. 减重步行训练机器人步态规划方法的研究. 中国康复医学杂志, 2008, 23(10): 916-918. DOI:10.3969/j.issn.1001-1242.2008.10.021 |
| [12] |
王企远. 步行康复训练机器人助行腿的步态规划与运动控制[博士学位论文]. 上海: 上海大学, 2011.
|
| [13] |
杨年峰. 人体运动协调规律及其参数化描述[博士学位论文]. 北京: 清华大学, 2001.
|
 2020, Vol. 29
2020, Vol. 29



