数控系统通常采用连续直线或圆弧对加工路径进行逼近来完成插补. 因多轨迹段的衔接处存在过渡拐角尖锐的特点, 所以对离散小线段加工时, 采用首位速度为零的加减速控制方式, 但该方法使整个插补过程中的速度方向连续突变, 即驱动轴的频繁启停会影响运动定位的精度. 针对以上问题, 张晓辉等[1]建立拐角曲线过渡模型, 保证轨迹衔接处的平滑性, 该算法使加工效率得到有效的提升, 但不能保证加工精度; Fan等[2]采用了基于样条曲线插补的轨迹规划算法, 此算法参数约束少且计算速度快, 但存在轨迹形状随速度变化而不可控的缺点. 许健等[3]提出一种基于有限项正弦级数的新位置规划算法来提高路径过渡的速度, 但速度比例参数过大会使得过渡速度很小, 不利于保持速度相对稳定. 关于速度规划技术在插补算法中的应用, Hu等[4]采用梯形加减速控制前瞻的进给速度, 但存在速度和加速度曲线过渡不平滑的问题; Cao等[5]将多路径段细分为直线段和圆弧小线段, 并对直线和圆弧轨迹的衔接处进行建模, 由轨迹的位移约束条件规划衔接点的最优速度, 但前瞻处理速度时, 采用对称S形加减速控制算法, 该算法在规划初末速度不同的路径段时缺乏灵活性; 冷洪滨等[6]采用三次多项式曲线代替复杂的S形曲线进行速度规划, 在加减速过程中实现了加加速度的连续, 但加加速度在加减速的始末位置仍然存在突变的情况. 为了进一步减少系统的柔性冲击, 王允森等[7]采用了四次多项式加减速算法、宁培志等[8]采用五次多项式加减速算法, 但上述算法需要大量的时间进行参数的计算, 实现较复杂; 史中权等[9]提出了一种加速度自适应调整的前瞻处理算法, 该算法在加速度的规划上更具灵活性, 但在轨迹的拐角处未考虑平滑过渡的问题.
基于以上研究现状, 提出了一种多轨迹段平滑过渡的前瞻插补算法. 该算法通过建立圆弧过渡模型进行相邻轨迹段的衔接, 并基于非对称S形加减速算法进行前瞻速度规划. 本文基于速度曲线拟合构造了一种新型柔性加减速算法, 并基于此算法对插补运算中的归一化因子进行求解, 使加速度过渡更加平稳. 最后将算法在Matlab端和伺服系统中均进行验证, 结果表明, 该算法可以使多轨迹段平滑过渡, 有效优化电机运动的平稳性, 提高末端执行器的精度和效率.
1 相邻轨迹段的圆弧过渡模型对于连续轨迹而言, 任意两直线段的连接处选用建立圆弧模型来进行拐角的平滑过渡处理[10]. 该算法可以根据特征点的坐标和半径调节等参数规划出过渡圆弧的圆心坐标、圆弧转接点坐标和拐角等参数.
如图1所示, Qn, vn, rn(n=1,2,3,···)(下同)分别为初始设定的路径目标点、速度和过渡圆弧半径; QTn, vTn, On分别是圆弧转接点、转接点速度和圆心; Kn为两圆弧转接点连线的中点; αn和ln分别为拐角大小和角平分线; dn为分割后的小路径段的长度.

|
图 1 相邻轨迹段的圆弧转接模型 |
由Q0, Q1, Q2构成的路径段转接模型为例进行求解, 设Q1坐标为(x1, y1, z1), 拐角α1存在如下函数关系:
| ${\alpha _1} = \arccos \dfrac{{\overrightarrow {{Q_1}{Q_0}} \cdot \overrightarrow {{Q_1}{Q_2}} }}{{\left| {\overrightarrow {{Q_1}{Q_0}} } \right|\left| {\overrightarrow {{Q_1}{Q_2}} } \right|}},{\alpha _1} \in \left( {0,\pi } \right)$ | (1) |
可以求得弧
| ${d_2} = (\pi - {\alpha _1}){r_1}$ | (2) |
由几何关系可得:
| $\left\{ {\begin{array}{*{20}{c}} {\overrightarrow {{Q_1}{Q_{T1}}} = \dfrac{{{r_1}}}{{\tan \dfrac{{{\alpha _1}}}{2}}} \cdot \dfrac{{\overrightarrow {{Q_1}{Q_0}} }}{{\left| {\overrightarrow {{Q_1}{Q_0}} } \right|}}} \\ {\overrightarrow {{Q_1}{Q_{T2}}} = \dfrac{{{r_1}}}{{\tan \dfrac{{{\alpha _1}}}{2}}} \cdot \dfrac{{\overrightarrow {{Q_1}{Q_2}} }}{{\left| {\overrightarrow {{Q_1}{Q_2}} } \right|}}} \end{array}} \right.$ | (3) |
由上式可计算得出QT1的坐标(xT1, yT1, zT1)为:
| $({x_{T1}},{y_{T1}},{{\textit{z}}_{T1}}) = ({x_1},{y_1},{{\textit{z}}_1}) + \overrightarrow {{Q_1}{Q_{T1}}} $ | (4) |
同理可以求得QT2的坐标值. 由Q0和QT1的坐标可求得直线长度d1的值, 因K1为QT1QT2的中点, 可得:
| $\overrightarrow {{Q_{T1}}{K_1}} = \dfrac{1}{2}\overrightarrow {{Q_{T1}}{Q_{T2}}} $ | (5) |
由式(5)可求得K1点坐标. 由图1中的几何关系可得:
| $\left| {\overrightarrow {{Q_1}{O_1}} } \right| = \dfrac{{{r_1}}}{{\sin ({\alpha _1}/2)}}$ | (6) |
| $\overrightarrow {{Q_1}{O_1}} = \left| {\overrightarrow {{Q_1}{O_1}} } \right| \cdot \dfrac{{\overrightarrow {{Q_1}{K_1}} }}{{\left| {\overrightarrow {{Q_1}{K_1}} } \right|}}$ | (7) |
将式(6)带入式(7)可求得O1点坐标. 圆弧转接模型的所有参数均求解完毕, 剩余转接模型可以此类推.
2 新型柔性加减速控制算法传统的余弦加减速算法通过余弦函数来计算出加速、匀速和减速段的执行时间和位移, 该算法采用的余弦函数的计算量较直线函数要大, 并没有充分利用三角函数加减速算法和直线形加减速算法在轨迹规划阶段计算结果一致的特点来简化计算. 对此提出一种新型柔加减速控制算法, 在轨迹规划时, 将直线形加减速算法代替余弦算法对加速段、匀速段和减速段的执行时间进行求解, 即在插补控制时, 将当前插补周期带入余弦加减速函数中进行曲线拟合[11]. 此算法能使速度和加速度的过渡更加连续平滑, 并减少传统余弦加减速算法的计算量.
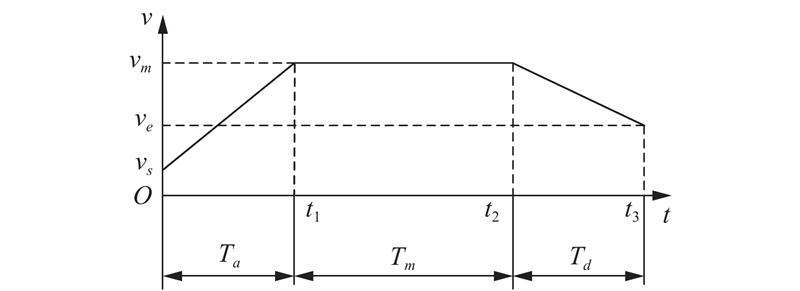
2.1 计算加减速段的执行时间由图2知, vs为初速度, vm为匀速运行时的速度, ve为末速度, 设a和d分别为加速段和减速段的加速度. 加速段时间Ta和运行位移Sa可分别表示为:
| $\left\{ \begin{array}{l} {T_a} = ({v_m} - {v_s})/a \\ {S_a} = ({v_m} + {v_s}){T_a}/2 \\ \end{array} \right.$ | (8) |
|
图 2 直线形加减速算法速度曲线 |
减速段的时间Td和运行位移Sd可分别表示为:
| $\left\{ \begin{array}{l} {T_d} = ({v_m} - {v_{\rm{e}}})/d \\ {S_d} = ({v_m} + {v_{\rm{e}}}){T_d}/2 \\ \end{array} \right.$ | (9) |
匀速段的运行位移Sm和执行时间Tm可分别表示为:
| $\left\{ \begin{array}{l} {S_m} = S - ({S_a} + {S_d}) \\ {T_m} = {S_m}/{v_m} \\ \end{array} \right.$ | (10) |
由图2可知:
| $\left\{ \begin{array}{l} {t_1} = {T_a} \\ {t_2} = {T_a} + {T_d} \\ {t_3} = {T_a} + {T_m} + {T_d} \\ \end{array} \right.$ | (11) |
由余弦加减速算法构造加速段的速度时间函数:
| $v(t) = \dfrac{1}{2}\left[ {{k_a} - {k_b}\cos (\dfrac{{\pi t}}{{{T_a}}})} \right]$ | (12) |
上式中,
| $\left\{ \begin{array}{l} {k_a} = ({v_m} + {v_e}) \\ {k_b} = ({v_m} - {v_s}) \\ \end{array} \right.$ | (13) |
因三角函数无限可导, 所以联立式(12)和(13)连续求导得到的加速度和加加速度均连续且有界, 从而提升系统的平稳性. 各速度段位移函数S(t)如下:
| $S(t) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{({v_m} + {v_s})t}}{2} - \dfrac{{{T_a}({v_m} - {v_s})}}{{2\pi }}\sin (\dfrac{{\pi t}}{{{T_a}}})},&{t \in \left[ {0,{t_1}} \right]} \\ {{v_m}(t - {T_a})},&{t \in \left( {{t_1},{t_2}} \right]} \\ {\dfrac{{({v_m} + {v_e})t}}{2} - \dfrac{{{T_a}({v_e} - {v_m})}}{{2\pi }}\sin (\dfrac{{\pi t}}{{{T_a}}})},&{t \in \left( {{t_2},{t_3}} \right]} \end{array}} \right.$ | (14) |
将式(8), (9)和式(10)的计算结果, 带入到(14)式中, 拟合出各阶段对应的新位移函数:
| $ S(t) = \left\{ \begin{array}{l} \dfrac{1}{2}({v_s} + {v_m})t - \dfrac{1}{2}({v_m} - {v_s}) \cdot \sin (\dfrac{{\pi t}}{{{T_a}}}) \cdot \dfrac{{{T_a}}}{\pi },\;\;t \in \left[ {0,{t_1}} \right]\\ S({t_1}) + {v_m}(t - {T_a}),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \in \left( {{t_1},{t_2}} \right]\\ S({t_1}) + S({t_2}) + \dfrac{1}{2}({v_m} + {v_e}) \cdot (t - {T_a} - {T_v}) + \\ \dfrac{{({v_m} - {v_e}){T_d}}}{{2\pi }} \cdot \sin \left[ {\dfrac{\pi }{{{T_d}}} \cdot (t - {T_a} - {T_v})} \right],\;\;\;\;\;\;t \in \left( {{t_2},{t_3}} \right] \end{array} \right. $ | (15) |
对式(15)中的各段位移函数S(t)分别求导即可得出系统对应不同阶段的速度函数:
| $v(t) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}({v_m} + {v_s}) - \dfrac{1}{2}({v_m} - {v_s}) \cdot \cos (\dfrac{{\pi t}}{{{T_a}}})},&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{t \in \left[ {0,{t_1}} \right]} \\ {{v_m}},&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{t \in \left( {{t_1},{t_2}} \right]} \\ {\dfrac{1}{2}({v_m} + {v_e}) + \dfrac{1}{2}({v_m} - {v_e})\cos \left[ {\dfrac{\pi }{{{T_d}}}(t - {T_a} - {T_v})} \right]},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{t \in \left( {{t_2},{t_3}} \right]} \end{array}} \right.$ | (16) |
同理, 对速度函数v(t)求导可得系统各段的加速度函数:
| $a(t) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{\pi }{{2{T_a}}}({v_m} - {v_s}) \cdot \sin (\dfrac{{\pi t}}{{{T_a}}}),}&{t \in \left[ {0,{t_1}} \right]} \\ 0,&{t \in \left( {{t_1},{t_2}} \right]} \\ {\dfrac{\pi }{{2{T_d}}}({v_e} - {v_m}) \cdot \sin \left[ {\dfrac{\pi }{{{T_d}}}(t - {T_a} - {T_v})} \right],}&{t \in \left( {{t_2},{t_3}} \right]} \end{array}} \right.$ | (17) |
系统的稳定性分析: 取式(15)~(17) 中加速段的位移、速度和加速度函数构造一个非线性系统: 取其李雅普诺夫函数V为:
| $V = {s^2} + {v^2}$ | (18) |
可知V正定. 沿系统的任意轨迹: 令V对t求导:
| $\dfrac{{dV}}{{dt}} = 2s\dot s + 2v\dot v = - 2{({s^2} + {v^2})^2}$ | (19) |
显然上式是负定的, 由李雅普诺夫稳定性定理可知: 该系统是渐进稳定的.
由式(15), 对各个阶段位移函数积分可得:
| $\left\{ \begin{array}{l} {S_1} = {T_a}({v_m} + {v_s})/2 \\ {S_2} = {S_1} + {v_c}{T_m} \\ {S_3} = {S_1} + {S_2} + {T_d}({v_m} + {v_e})/2 \\ \end{array} \right.$ | (20) |
将上式与式(8)~(10)对比可知, 式(20)的结果与直线形加减速算法中的位移公式相同. 这就很大程度上简化了速度前瞻和轨迹规划时的运算量.
2.3 基于Matlab的仿真对比(1) 在Matlab程序中设定同一组参数, 即位移为50 mm, 初速度为0 mm/s, 末速度为8 mm/s, 最大速度为40 mm/s, 最大加速度为110 mm/s2. 对传统余弦算法和新型柔性算法的运算效率进行仿真对比. 得到的运动学曲线如图3, 各速度段执行时间如表1.

|
图 3 余弦算法与新型柔性算法的速度曲线 |
| 表 1 两种算法各速度段的运算时间(单位: s) |
由图3和表1所示的仿真结果表明: 同一组参数约束下, 新型柔性算法运算总时间更短, 可有效减小原余弦加减速算法的运算量, 提升运算的实时性.
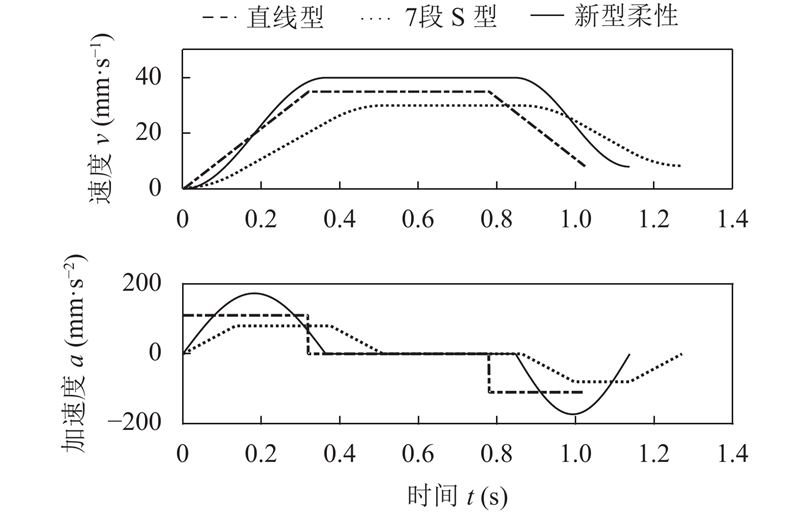
(2) 对新型柔性加减速算法、直线形加减速算法及传统7段S形加减速算法进行仿真, 得到的运动学曲线对比如图4所示.
由图4可知: 相较于直线形加减速算法, 新型柔性加减速算法的速度过渡更加平滑; 相较于传统7段S形加减速算法, 新型算法的加速度过渡的平滑性得到有效改善, 算法构造的过程更简洁; 新型加减速算法的速度曲线根据给定的参数约束条件不同而呈现非对称的状态, 满足多路径段规划时的外界约束要求.
|
图 4 3种加减速算法的运动学曲线对比图 |
3 前瞻插补算法设计
前瞻控制技术的两个关键点是加减速控制和连续轨迹段间的衔接速度处理[12,13], 算法设计如下.
3.1 加减速控制算法轨迹规划中的速度控制部分由非对称S形加减速算法[14,15]进行规划, 该算法的运动学曲线如图5所示.

|
图 5 非对称S形加减速算法的运动学曲线 |
由图5所示的运动学曲线可知, 时间ta~tg将整个速度曲线分为加加速、匀加速、减加速、匀速、减减速、匀减速和加减速7个阶段; v0, vmax, v1分别为初速度, 设定最大速度和末速度; amax和amin分别是加速度的最大值和最小值; jmax和jmin分别代表加加速度的最大值和最小值. 下节将按照非对称S形加减速算法对连续轨迹的细分小线段进行速度的规划.
3.2 轨迹衔接速度处理以图1中Q0Q1QT3构成的拐角为例, 由非对称S形加减速控制方法将轨迹段中的直线段Q0QT1和QT2QT3进行加减速规划, 对衔接圆弧QT1QT2做匀速处理. 为了使末端执行器高效率运行, 将圆弧段的速度规划为相邻直线段的可达最大速度vlim. 具体如下:
若满足:
| $({v_{\max }} - {v_0}){j_{\max }} < {a_{\max }}^2$ | (21) |
则加速段的时间Tsa可以求为:
| $\left\{ \begin{array}{l} {t_a} = \sqrt {({v_{\max }} - {v_0})/{j_{\max }}} \\ {T_{sa}} = 2{t_a} \\ \end{array} \right.$ | (22) |
否则按下式求解:
| $\left\{ \begin{array}{l} {t_a} = {a_{\max }}/{j_{\max }} \\ {T_{sa}} = {t_a} + ({v_{\max }} - {v_0})/{a_{\max }} \\ \end{array} \right.$ | (23) |
若满足:
| $({v_{\max }} - {v_1}){j_{\max }} < {a_{\max }}^2$ | (24) |
则减速段的时间Tsd按下式求解:
| $\left\{ \begin{array}{l} {t_e} - {t_d} = \sqrt {({v_{\max }} - {v_1})/{j_{\max }}} \\ {T_{sd}} = 2({t_e} - {t_d}) \\ \end{array} \right.$ | (25) |
否则按下式求解:
| $\left\{ \begin{array}{l} {t_e} - {t_d} = {a_{\max }}/{j_{\max }} \\ {T_{sd}} = {t_e} - {t_d} + ({v_{\max }} - {v_1})/{a_{\max }} \\ \end{array} \right.$ | (26) |
匀速段时间Tsv可求解为:
| ${T_{sv}} = \dfrac{{{q_1} - {q_0}}}{{{v_{\max }}}} - \dfrac{{{T_{sa}}}}{2}(1 + \dfrac{{{v_0}}}{{{v_{\max }}}}) - \dfrac{{{T_{sd}}}}{2}(1 + \dfrac{{{v_1}}}{{{v_{\max }}}})$ | (27) |
上式中, q0和q1分别代表初末位置; 若Tsv>0, 即存在匀速段, 则系统的限制最大速度vlim取vmax; 若Tsv≤0, 则vlim<vmax.
加速直线段Q0QT1的速度与时间如下函数关系:
| $v = \left\{ {\begin{array}{*{20}{l}} {{v_0} + {j_{\max }}{t^2}/2}&{t \in \left[ {0,{t_a}} \right)} \\ {{v_0} + a(t - {t_a}/2)}&{t \in \left[ {{t_a},{t_b}} \right)} \\ {{v_{\rm {lim}}} - {j_{\max }}{{({T_{sa}} - t)}^2}/2}&{t \in \left[ {{t_b},{t_c}} \right)} \\ {{v_{\rm {lim} }}}&{t \in \left[ {{t_c},{t_d}} \right)} \end{array}} \right.$ | (28) |
减速直线段QT2QT3的速度时间存在以下函数关系:
| $v = \left\{ {\begin{array}{*{20}{l}} {{v_{\rm {lim }}} - \dfrac{{{j_{\max }}{{(t - {t_g} + {T_{sd}})}^2}}}{2}}&{t \in \left[ {{t_d},{t_e}} \right)} \\ {{v_{\rm {lim}}} + \dfrac{{a(t - {t_g} + {T_{sd}} - ({t_e} - {t_d}))}}{2}}&{t \in \left[ {{t_e},{t_f}} \right)} \\ {{v_1} + \dfrac{{{j_{\max }}{{({t_g} - t)}^2}}}{2}}&{t \in \left[ {{t_f},{t_g}} \right]} \end{array}} \right.$ | (29) |
将两直线段中间的衔接圆弧QT1QT2的速度规划为vlim, 至此, 连续轨迹段间的衔接速度规划完毕.
3.3 位置插补以Q0QT1段为例, 设起始点Q0的坐标为(x1, y1, z1). 中间插值点的位置坐标(x, y, z)可以表示为:
| $\left\{ {\begin{array}{*{20}{c}} {x = {x_1} + \lambda \Delta x} \\ {y = {y_1} + \lambda \Delta y} \\ {{\textit{z}} = {{\textit{z}}_1} + \lambda \Delta {\textit{z}}} \end{array}} \right.$ | (30) |
式中, λ为归一化因子, (△x, △y, △z)代表首末位置间的增量. 故插补问题转变为对归一化因子λ的求解. 传统的插补算法基于抛物线过渡的方式对归一化因子进行求解, 但规划得出的速度和加速度曲线的并不连续, 这会加剧系统振荡. 本文将采用新型柔性速度规划算法来进行归一化参数的求解.
为简化算法, 根据第2节内容将新型柔性加减速算法的速度做对称处理. 设加速阶段的时间为T1, 位移为S1, 匀速阶段末端的时间为T2, 位移为S2, 总的运动时间为Tsum, 总位移为Ssum. 设末端执行器在匀速运动时的线速度为v2, 基于直线形加减速算法求解各段速度的时间时, 设加速度和减速度的值为a_n, 则可以计算出加速阶段的时间和位移分别为:
| $\left\{ \begin{array}{l} {T_1} = \dfrac{{{v_2}}}{{a{\_{_n}}}} \\ {S_1} = \dfrac{{{T_1}^2a{\_{_n}}}}{2} \end{array} \right.$ | (31) |
总时间Tsum为:
| ${T_{\rm {sum}}} = 2{T_1} + (S - 2{S_1})/{v_2}$ | (32) |
将位移、时间和加速度参数进行归一化处理:
| $\left\{ \begin{array}{l} {S_{1\lambda }} = {S_1}/{S_{\rm {sum}}} \\ {T_{1\lambda }} = {T_1}/{T_{\rm {sum}}} \\ {T_{2\lambda }} = 1 - 2{T_{1\lambda }} \\ {a_\lambda } = 2{S_{1\lambda }}/{T_{1\lambda }}^2 \\ \end{array} \right.$ | (33) |
上式中, S1λ, T1λ, T2λ, aλ分别是S1, T1, T2, a_n的归一化参数, 结合新型柔性型速度规划算法的位移公式, 对归一化因子λ进行求解:
| $\lambda = \left\{ \begin{array}{l} \dfrac{{{v_2}t}}{2} - \dfrac{{{T_{1\lambda }}{v_s}}}{{2\pi }}\sin (\dfrac{{\pi t}}{{{T_{1\lambda }}}}),\;\;\;\;0 \le t \le {T_{1\lambda }}\\ \dfrac{{{v_2}{T_{1\lambda }}}}{2} + {v_2}(t - {T_{1\lambda }}),\;\;\;\;\;\;{T_{1\lambda }} < t \le {T_{2\lambda }}\\ \dfrac{{{v_2}{T_{1\lambda }}}}{2} + {v_2}({T_{2\lambda }} - {T_{1\lambda }}) + \dfrac{{{v_2}(t - {T_{2\lambda }})}}{2} + \\ \dfrac{{{T_{1\lambda }}{v_2}}}{{2\pi }}\sin \left[ {\dfrac{{\pi (t - {T_{2\lambda }})}}{{{T_{1\lambda }}}}} \right],{T_{2\lambda }} < t \le 1 \end{array} \right.$ | (34) |
上式中, t代表当前时刻, 且t=i/N, (0≤t≤1), i=1, 2, 3,···,N, 其中N代表总的插值点数, 通过下式来计算:
| $N = {P_n}\dfrac{X}{{{Y}}}$ | (35) |
式中, Pn是插值参数, 用于增加插值点数; X和Y在直线插补中分别表示末端执行器的总位移和线速度; 在圆弧插补中分别表示末端执行器的圆心角和角速度. 每个插值点的时间值, 都有一个λ与之对应, 且0≤λ≤1, 结合式(30)即可得到各个插值点的位置坐标.
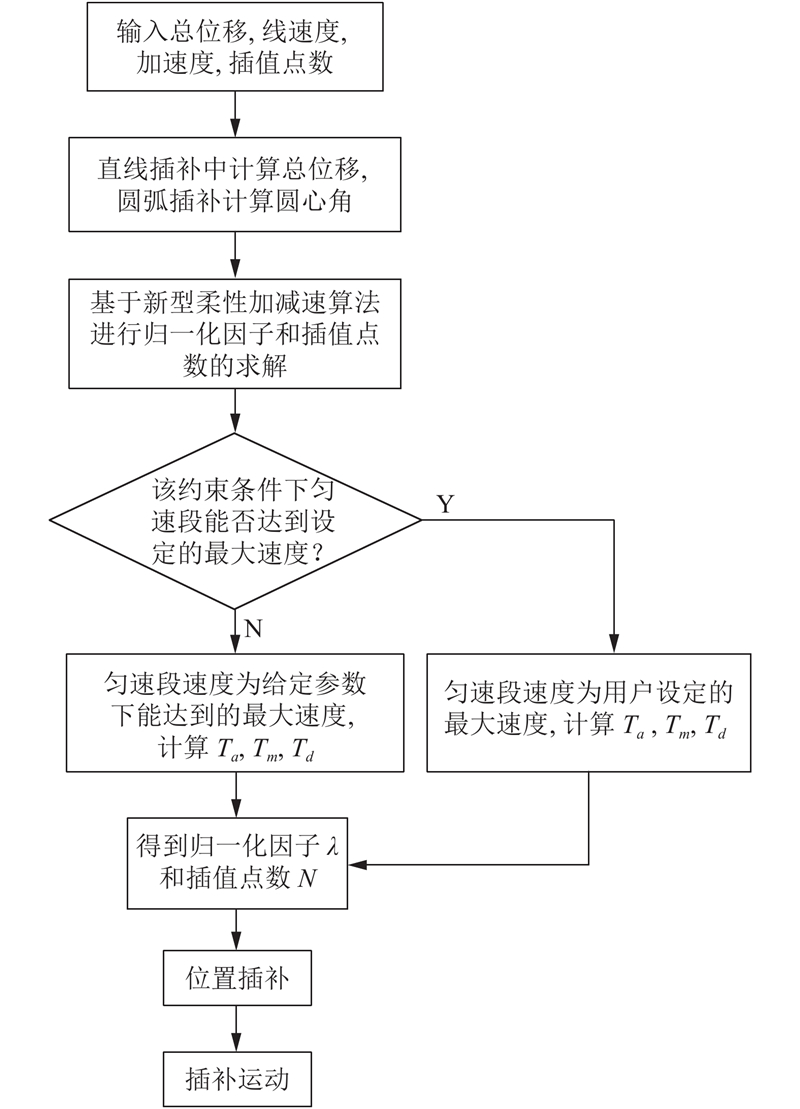
3.4 插补算法流程插补算法流程如图6.
|
图 6 插补算法流程图 |
4 实验测试与结果分析 4.1 基于Matlab的多段轨迹过渡实验
设定目标曲线是由9条线段组成的连续轨迹, 给定如表2的位置坐标、过渡圆弧段的速度参数及其半径参数; 设定系统允许的最大加速度amax=600 mm/s2, 最大加加速度jmax=3000 mm/s3, 插补周期为0.002 s, 将以上参数初始化并进行空间插补运算, 对比传统算法和平滑过渡前瞻算法得到的轨迹效果及运动学曲线.
| 表 2 实验一给定实验参数 |
方法一: 传统算法采用多轨迹段初末速度为零的加减速控制方式. 由方法一规划的空间轨迹效果如图7所示; 其的运动学曲线如图8所示.

|
图 7 传统算法规划的空间轨迹 |

|
图 8 传统算法规划的速度和加速度曲线 |
由图8中的速度曲线可知, 传统的控制方式存在频繁启停的问题, 容易引起振动并对运动轴造成冲击. 基于方法一计算得到的总执行时间为5.2636 s.
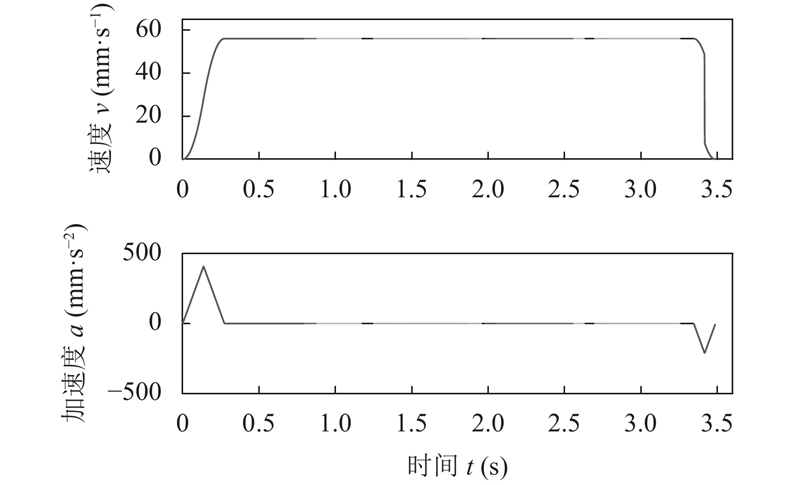
方法二: 采用多轨迹段平滑过渡的前瞻算法, 过渡圆弧半径设为r=3 mm, 其余参数同方法一. 由方法二规划的空间轨迹效果如图9所示; 其运行学曲线如图10所示.

|
图 9 平滑过渡前瞻算法规划的空间轨迹 |
|
图 10 平滑过渡的前瞻算法规划的运动学曲线 |
对比图7和图9可知, 由方法二规划得到的轨迹轮廓过渡的更加平滑; 对比图8和图10可知, 速度前瞻插补算法将过渡圆弧的速度规划为相邻直线段能达到的最大速度, 提升了末端执行器速度的连续性和平稳性; 基于方法二计算得到的总执行时间为3.4877 s, 相较于方法一, 该算法将执行效率提升近33.8%.
4.2 基于工控机的测试与分析实验平台(如图11)的上位机采用研华的工控机, 处理器是intel(R)Core(TM)i5-4460, CPU频率是3.20 GHz, 系统内存为8 GB. 上位机软件TwinCAT通过EtherCAT总线实现TwinCAT和伺服驱动器的实时通信, 并可以完成人机界面的搭建. 按表3将规划后的位置坐标下发给伺服驱动器, 速度和加速度数据由机械手末端电机的编码器进行采集, 并在上位机界面中实时显示.
在上位机软件中进行程序编写和设定参数. 设定最大加速度amax=600 mm/s2, 最大加加速度jmax=3000 mm/s3, 插补周期为0.002 s. 实验通过限制拐点处不同的最大速度来检验加减速控制的平稳性, 并分析过渡圆弧的半径参数对于插补效率的影响. 由编码器采集的三组半径参数对应的数据绘制而成的速度和加速度曲线分别如图12和图13所示.
| 表 3 初始化参数 |
由图13可知, 在设定最大加速度为600 mm/s2时,电机的最大加速度为378 mm/s2, 表明本文前瞻算法在速度的约束下, 对加速度做出了自适应的调整, 证明了算法的可行性; 由图12和图13可知, 当拐角半径参数设定为1.6 mm时, 系统的运行时间为6.9251 s; 当半径设定为4.2 mm时, 系统的运行时间为6.8409 s; 当半径设定为7.3 mm时, 系统的执行时间为6.7273 s, 系统的执行时间随设定半径参数的变化而变化.

|
图 11 实验平台示意图 |

|
图 12 规划的速度曲线 |
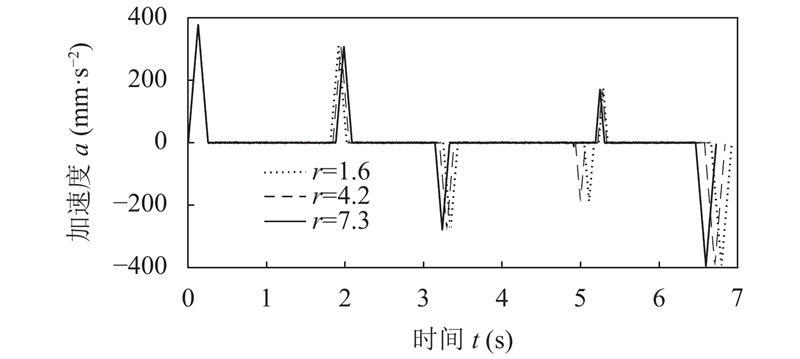
|
图 13 规划的加速度曲线 |
本实验结果表明:
(1) 在不同的速度约束下, 前瞻插补算法可以自适应调整速度和加速度, 保证了速度过渡的平稳性;
(2) 因多轨迹段之间靠圆弧衔接, 所以每段轨迹规划的初末速度不必减小为零, 即不存在电机频繁启停的问题, 有效的提升了加工效率, 验证了该前瞻算法的对每小段轨迹衔接速度处理的有效性和优越性;
(3) 本文算法对参数设定进行了简化, 用户可在上位机界面设定半径参数对目标轨迹做理想的修形处理, 也可根据插补效率随过渡圆弧半径参数的不同而不同的特点, 设定最优的半径参数来使系统的加工效率最大化; 给定的速度和加速度参数可作为算法应用硬件平台的最大限制速度, 进而防止轨迹形状因速度变化而出现不可控的缺点.
5 结论多轨迹段平滑过渡的前瞻插补算法能够使插补轮廓曲线更加圆滑, 有效解决了传统多轨迹段初末速度为零的加减速控制方式带来的频繁启停问题, 并且用户可以调节半径参数对轨迹进行修形处理; 该算法采用的速度前瞻技术可以规划出多轨迹段衔接圆弧的最优速度, 并实时计算下一插补周期的执行速度, 使末端执行器的运动具有连续性, 有助于提高机床的实际运行效率; 在插补算法的设计中, 相较于基于抛物线过渡和传统余弦过渡的插补算法, 基于新型柔性加减速控制算法的空间插补算法对于速度和加速度的连续性均有稳定的提升, 适用于精度要求较高的场合.
| [1] |
张晓辉, 于东, 杨东升, 等. 面向微线段高速加工的拐角曲线过渡插补算法. 机械工程学报, 2010, 46(19): 183-191. |
| [2] |
Fan W, Lee CH, Chen JH. A realtime curvature-smooth interpolation scheme and motion planning for CNC machining of short line segments. International Journal of Machine Tools and Manufacture, 2015, 96: 27-46. DOI:10.1016/j.ijmachtools.2015.04.009 |
| [3] |
许健, 梅江平, 段晓斌, 等. 一种工业机器人连续轨迹规划过渡算法. 工程设计学报, 2016, 23(6): 537-543. |
| [4] |
Hu J, Xiao LJ, Wang YH, et al. An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead. The International Journal of Advanced Manufacturing Technology, 2006, 28(9–10): 930-935. DOI:10.1007/s00170-004-1884-2 |
| [5] |
Cao YN, Wang TM, Chen YD, et al. A high-speed control algorithm using look-ahead strategy in CNC systems. Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications. Singapore. 2008. 372–377.
|
| [6] |
冷洪滨, 邬义杰, 潘晓弘. 三次多项式型微段高速加工速度规划算法研究. 计算机集成制造系统, 2008, 14(2): 336-340, 397. |
| [7] |
王允森, 盖荣丽, 孙一兰, 等. 高质量加工中四次多项式速度规划算法研究. 中国机械工程, 2014, 25(5): 636-641. DOI:10.3969/j.issn.1004-132X.2014.05.013 |
| [8] |
宁培志, 毕庆贞, 王宇晗, 等. 基于五次速度曲线的高柔性加减速前看算法. 组合机床与自动化加工技术, 2014(4): 15-18. |
| [9] |
史中权, 叶文华. 多轴联动条件下插补速度实时可调的前瞻控制算法. 航空学报, 2014, 35(2): 582-592. |
| [10] |
王斌锐, 王涛, 李正刚, 等. 多路径段平滑过渡的自适应前瞻位姿插补算法. 控制与决策, 2019, 34(6): 1211-1218. |
| [11] |
钟前进, 王科, 丁信忠. 一种新型S加减速算法研究. 电气传动, 2019, 49(6): 8-12, 37. |
| [12] |
潘海鸿, 杨增启, 陈琳, 等. 一种优化轨迹段间衔接速度的自适应前瞻控制. 机械工程学报, 2015, 51(5): 151-159. |
| [13] |
李浩, 吴文江, 韩文业, 等. 基于自适应前瞻和预测校正的实时柔性加减速控制算法. 中国机械工程, 2019, 30(6): 690-699. |
| [14] |
潘海鸿, 袁山山, 黄旭丰, 等. 全类型非对称七段式S型曲线加减速控制算法研究. 机械科学与技术, 2018, 37(12): 1928-1935. |
| [15] |
朱明, 游有鹏, 何均. S形加减速算法前瞻处理研究. 小型微型计算机系统, 2011, 32(10): 2140-2144. |
 2020, Vol. 29
2020, Vol. 29



