2. 广州工商学院 计算机科学与工程系, 广州 510850
2. College of Computer Science and Engineering, Guangzhou College of Technology and Business, Guangzhou 510850, China
深度学习是机器学习的一个子集, 通过组合低层特征形成更加抽象的高层语义以发现数据的特征分布表示. Hinton等人[1]提出, 深度置信网络(Deep Belief Network, DBN)的训练可以由非监督逐层训练以及后期微调的方式完成. 这为解决深层神经网络结构相关的训练优化难题带来希望. 但是在2012年之前, 深度学习仍然处于理论研究阶段, 还没有真正进入应用阶段. 这受制于两个原因, 第一是深度模型的训练需要大批量数据, 当时在模型预训练阶段一般采用ImageNet[2]数据集或其子集; 第二是计算力特别是GPU等硬件设备还没能够提供强大计算支持. 2012年, 在ImageNet图像识别竞赛中, Hinton和他的学生Alex Krizhevsky设计出AlexNet[3]神经网络结构, 并以此在这次比赛中获得冠军. 这成为深度学习应用领域的标志性事件. 之后各种神经网络结构应运而生. 深度学习应用领域比较成功的有计算机视觉、自然语言处理、语音识别、目标检测等. 其中计算机视觉领域常用的基础网络结构有AlexNet、VGGNet[4]、GoogleNet[5]、ResNet[6]、denseNet[7]、mobileNet[8]、shuffleNet[9, 10]等. 这些基础网络[3-10]在实际应用中表现各有优劣. Goodfellow[11, 12]提出, 一个测试效果良好的分类器并不是学习到了所分类样本的真正底层意义, 只不过刚好构建了一个在训练数据上运行相当良好的模型, 而这个模型遇到一些空间中不太可能出现的点时, 模型能力的有限性就会随之暴露出来. 这个可能也就是许多模型对于外来样本泛化能力不足的原因.
深度学习会自动学习数据集上的特征分布. 一般而言, 数据需要尽可能地保持独立同分布. 但是实际情况由于各种条件的限制, 独立同分布往往是不可能做到的. 当非独立同分布的数据量比较大, 会严重影响模型对数据特征的有效学习, 模型的鲁棒性得不到保证. 实际应用中针对特定任务需要采集和标注适合自己任务的数据集, 这些数据的独立同分布特性往往得不到保证. 当然, 有关联的数据往往被用作上下文信息, 但就数据的角度看, 这些有关联的数据是不符合机器学习的独立同分布假设的.
本文研究分别采用了LeNet-5[13], VGGNet16, ResNet50作为基础网络, 实验对比发现, 批规范化算法[14](Batch Normalization, BN)有非常大的可调空间, 其对最终的分类和检测识别结果也有一定程度的影响. 实验观察出该算法有下面三点不足:
(1) 批规范化算法在模型训练时要求有足够大的批量才能工作. 如果每批的数据量太少则会导致对统计数据的估计不准确. 每批的数据量减少则会显著增加模型误差. 现在的模型训练, 如果硬件设备条件允许, 则是采用大批量数据来训练的. 而这大批量数据中非独立同分布数据也可能比较多.
(2) 批规范化算法做规范化运算时, 每批的输出与这批量数据的每一个样本都有关联. 这从批规范化的计算公式可以看出.
(3) 目标检测、分割、视频识别和其他基于此的高级系统对批量大小的限制要求更高. 如Faster[15]和Mask R-CNN[16]系列检测框架使用批量为1或2的图像, 为了能够使用更高分辨率的图像, 批规范化算法通过变换而被线性层所固定.
基于以上3个观察, 本文提出批规范化算法的改进算法. 该改进算法在模型训练前, 在数据集中固定一个批量数据, 对该批量数据做规范化计算后, 其结果作为参考值对训练中的其他数据进行更新运算. 提高该改进策略, 实验效果比较明显.
1 相关工作在神经网络训练过程中, 网络隐层的输入分布经常变化, 如果要使训练数据获得的模型能够有泛化能力, 就须使训练数据与测试数据满足独立同分布假设. 批规范化算法的初衷是使神经网络训练过程中输入分布保持一致, 即把神经网络每一层神经元输入值的分布规范化为标准正态分布. 这就很大程度防止了训练过程中的梯度消失问题. 在反向传播时以批为单位进行梯度更新, 极大加快了网络训练速度.
当批量数据样本很少的时候, 非独立同分布问题越来越显现, 模型的泛化能力大幅度降低, 模型也难以训练. 为解决这个问题, 批再规范化算法[17](Batch ReNormalization, B-RN)在批规范化算法基础上引入两个参数, 通过对权重的尺度(scale)和偏移(shift)去适应一个小批量数据, 然后移动平均值消除归一化后的激活值对当前批量数据的依赖性. 其本质是网络参数前传中仿射变换修正小批量数据和数据集普适样本的差异, 使得该层的激活值在推断阶段能得到更有泛化性的修正.
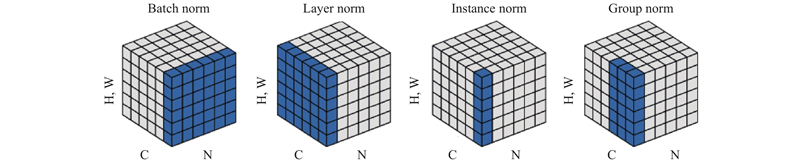
批规范化算法主要适用于CNN或者DNN这种有固定深度的神经网络, 而在RNN中, 序列(sequence)的长度不一致, 不同的时间步(time-step)需要保存不同的统计特征, 可能存在一个特殊序列比其他序列长很多. 即RNN的深度不固定. 因此, 批规范化算法在RNN上效果不理想. 层规范化算法[18](Layer Normalization, LN)不依赖于批量数据的大小和输入序列的深度, 同一层的输入样本拥有相同的均值和方差, 而不同的输入样本有不同的均值和方差. 如图1所示, 层规范化算法不在批量维度上做规范化, 而是在层的维度上做规范化. 层规范化算法在RNN中效果明显.
|
图 1 各种规范化算法示例 |
图像风格化应用中, 生成结果依赖于某个图像实例, 因此也不能在批量数据的维度进行归范化操作. 实例规范化算法[19](Instance Normalization, IN)在HW的维度做规范化操作, 可以加速模型收敛, 并且保持每个图像实例之间的独立.
自适配规范化算法[20](Switchable Normalization, SN)使用可微分学习, 为一个深度网络中的每一个需要做规范化操作的层确定合适的规范化操作. 区别于BN需要手工为每一个规范化层设计操作, 自适配规范化算法的这个特性可以减少手工设计量, 省去大量的实验.
群组规范化算法[21](Group Normalization, GN)在通道的维度分组, 并在每组内进行规范化操作, 计算出均值和方差. 群组规范化算法的计算与批量数据的大小无关, 并且在神经网络模型训练时, 其准确度在大范围的批量下运行都非常稳定.
2 批规范化算法令X={x1, x2, ···, xN}为训练数据集, 在神经网络训练时, 可令损失函数:
| $ l = F(x,\Theta ) $ | (1) |
其中, F为每一层的非线性转换函数. 因此, 对于每一个样本, 使用随机梯度下降法[22, 23](Stochastic Gradient Descent, SGD)计算最优化参数
| $ \Theta = \arg \mathop {\min }\limits_\Theta \frac{1}{N}\sum\limits_{i = 1}^N l \left( {{x_i},\Theta } \right) $ | (2) |
在该数据集中取一个批量数据B={x1, x2,···, xm}, 用该批量数据的平均梯度去拟合该批量数据每一个样本的梯度, 即:
| $ \frac{1}{m}\frac{{\partial l\left( {{x_i},\Theta } \right)}}{{\partial \Theta }} $ | (3) |
由式(1)可知, 对于每一层收入x, 有:
| $ l = {F_2}\left( {{F_1}\left( {x,{\Theta _1}} \right),{\Theta _2}} \right) $ | (4) |
因此可知, 每一个梯度优化步骤为:
| $ {\Theta _2} \leftarrow {\Theta _2} - \frac{\alpha }{m}\sum\limits_{i = 1}^m {\frac{{\partial {F_2}\left( {{x_i},{\Theta _2}} \right)}}{{\partial {\Theta _2}}}} $ | (5) |
其中,
上述过程是典型的随机梯度优化过程. 大量的实验经验表明, 如果在神经网络训练过程中, 简单地使用随机梯度下降法会使训练的计算量和时间大大增加. 而且, 经过非线性转换函数F(*)的作用, 每一层的输出不能保持同分布状态, 模型难以训练, 并且表达能力有限, 致使泛化性能降低. 因此, 批规范化算法引入两个可学习参数
| $ y=\gamma \overset\frown{x}+\beta $ | (6) |
对于每一层输入x, 有:
| $ \overset\frown{x}=\frac{x-\mu }{\delta } $ | (7) |
其中,
| $ \gamma =\delta $ | (8) |
| $ \beta =\mu $ | (9) |
时, 神经网络训练时的每一层即可保持标准正态分布. 因此, 由以上分析, 令批规范化转换表示为:
| $ {{B}}{{{N}}_{\gamma ,\beta }}:{x_i} \to {y_i} $ | (10) |
本文给出批规范化转换算法伪代码描述如算法1. 其中,
算法1. 批规范化变换算法
输入: 批量数据B={x1, x2, ···, xm};
需学习的参数
输出:
开始:
1.
2.
3.
4.
结束
3 批规范化改进算法本文在第一章相关工作中介绍了批规范化算法的几个改进算法[18-21]. 该系列算法针对批规范化算法的许多不足之处做出改进. 但是各有其使用场景. 本文提出一种批规范化改进算法, 一定程度上解决神经网络训练过程中数据不能保持独立同分布问题. 即: 每一层批量数据的输出与这批量数据的每一个样本都有关联. 该改进算法即是降低这种数据的关联性.
该改进算法分为3步:
(1) 神经网络训练时, 每一层的输入数据中, 取出一个批量数据, 按照算法1取出该批量数据的均值和方差, 这两个统计数据在之后训练时固定下来保持不变. 令Bfix={x1, x2, ···, xm}, 则:
| $ {{\mu _{{\rm{fix }}}} \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{x_i}} } $ | (11) |
| $ {\delta _{{\rm{fix }}}^2 \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{x_i} - {\mu _{{\rm{fix }}}}} \right)}^2}} } $ | (12) |
(2) 求出其他批量数据的均值和方差, 并根据批量数据的样本量求出其他批量数据与固定批量数据的比例系数, 根据该比例系数更新其他批量数据的均值和方差. 令:
| $ {\lambda _1} = \frac{1}{{m + 1}} $ | (13) |
| $ {\lambda _2} = 1 - {\lambda _1} $ | (14) |
则其他批量数据的均值和方差更新方式为:
| $ {{\mu _{{\rm{others }}}} \leftarrow {\lambda _2} \cdot {\mu _{{\rm{others }}}} + {\lambda _1} \cdot {\mu _{{\rm{fix }}}}} $ | (15) |
| $ {\delta _{{\rm{others }}}^2 \leftarrow {\lambda _2} \cdot \delta _{{\rm{others }}}^2 + {\lambda _1} \cdot \delta _{{\rm{fix }}}^2} $ | (16) |
(3) 根据(2)得出的
根据以上分析, 可以得出批规范化改进算法的伪代码描述如算法2.
算法2. 批规范化变换改进算法
输入: 批量数据Bfix={z1, z2, ···, zm};
批量数据B={x1, x2, ···, xm};
需学习的参数
输出:
开始:
1.
2.
3.
4.
5.
6.
7.
8.
结束
给定一个神经网络, 加入批规范化改进算法后的训练和推断方式与批规范化算法无异. 下面给出具有批规范化改进算法网络层的神经网络训练和推断算法描述如算法3.
算法3. 神经网络训练与推断
输入: 神经网络Net; 可训练参数
每一层的输入
输出: 推断网络
开始:
1. 初始化训练网络
2. for k=1 to K do
3. 根据算法2在该训练
4. 修改
5. end for
6. 优化
7. 训练好网络后
8. for k=1 to K do
9. 对多个大小为m的批量数据B, 计算:
10. 在推断网络
11. end for
结束
4 实验 4.1 实验环境本文算法的实验环境配置为Intel I7 8700处理器, 8块NVIDIA GTX 1080ti显卡, 64 GB RAM的深度学习服务器. 软件环境配置为Ubuntu 16系统, GCC 5.4, CUDA 9, OpenCV 3, TensorFlow, Caffe/Caffe2, Detectron框架等.
4.2 实验结果及分析为了验证算法各方面性能, 本文进行了3组对比实验, 分别为训练速度对比, ImageNet分类实验, 目标检测实验.
4.2.1 模型训练速度对比为了快速得到训练结果, 简化调参步骤, 使实验对照组更具说服力, 该组对比实验模型选用LeNet-5和VGG-16, 数据集选用Mnist, 对比算法选用批规范化算法以及本文改进算法. 图2和图3分别说明了批规范化算法和改进算法在Mnist数据集上两个神经网络模型的训练情况.
|
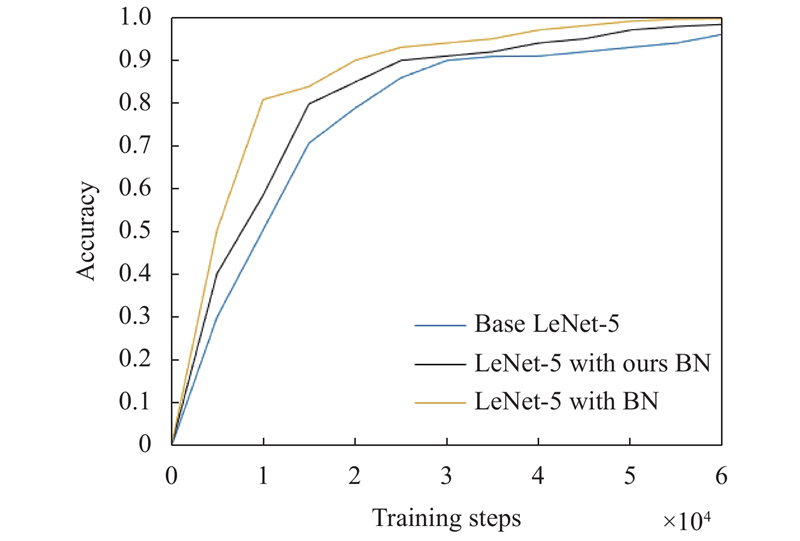
图 2 LeNet-5训练曲线 |
由图2和图3训练曲线可以看出, 在Mnist数据集上, LeNet-5和VGG-16的3条曲线的趋势大致是一样的, 随着训练步的增加, 训练精度分别呈上升趋势.
在模型训练过程中, 相对于没有规范化操作的LeNet-5或者VGG-16网络, 加入本文改进算法后, 网络模型训练速度有所提高, 特别是在训练的前期, 改进后的模型更快的进入饱和点. 图2中在训练步为26 000时可以看出, 3条曲线的斜率变缓, 模型训练进入饱和阶段. 其中, 批规范化算法最先进入饱和点, 其次本文改进算法进入饱和点, 没有进行规范化操作的LeNet-5最后进入饱和点. 图3中VGG曲线也遵循这个趋势.

|
图 3 VGG-16训练曲线 |
由图2和图3也可以对比得出, 在训练速度上, 改进算法可以加快网络模型的训练, 但是相对于批规范化算法, 改进算法没有明显优势. 可能的原因在于, 在设计改进算法时引入了一个固定批量数据, 对其做了规范化操作. 因此, 改进算法相对于原批规范化算法, 相当于做了两次规范化操作. 计算量有所增加, 体现在训练曲线上即为饱和点右移.
4.2.2 ImageNet数据集分类实验该组实验采用ResNet50作为基准网络, 在ImageNet数据集上进行分类训练. 实验采用了8块GPU, 批规范化运算时, 批量数据的均值和方差将在不同的GPU上进行计算. 卷积层初始化采用He等 [24]的方法,
为了作对比, 本文在ResNet50基准网络上分别采用BN、LN、IN、GN以及本文改进算法Ours进行分类训练.
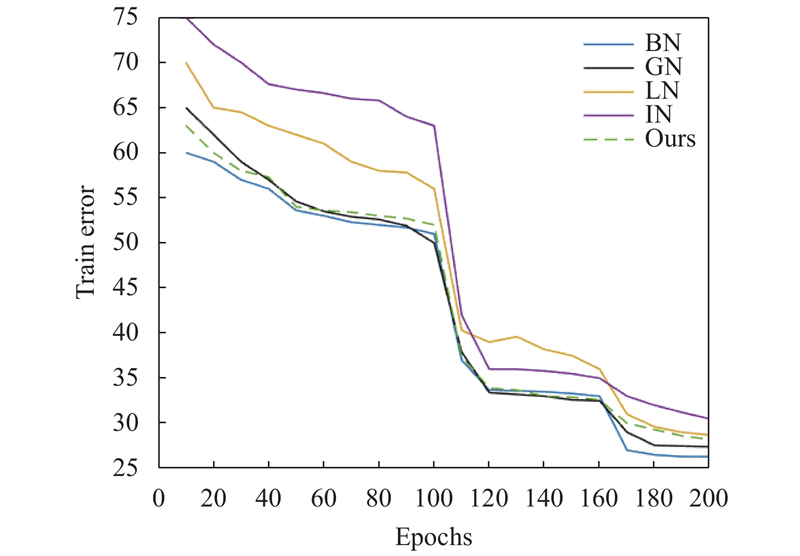
图4和图5分别为ImageNet训练集和验证集上的训练曲线. 因为几个算法都是在BN算法的基础上改进而来, 本实验以BN算法作为基准对比组. 由图4和图5可以看出, ResNet50在模型训练时, 引入5种算法后都能够收敛. 此时规范化批量数据大小为128, 群组规范化算法的分组数为32. 表1和表2列出了ResNet50基准网络引入5种算法后在ImageNet训练集和验证集上训练错误率.
|
图 4 ImageNet训练error曲线 |

|
图 5 ImageNet验证集训练error曲线 |
| 表 1 ImageNet训练集结果对比(%) |
| 表 2 ImageNet验证集结果对比(%) |
分析表1, 可以看出BN算法在批量数据大小为128时, 错误率比其它5个算法低. 相对于BN算法训练集上26.3%的错误率, GN算法高出1.1个百分点, 本文的改进算法Ours高出1.9个百分点. 而LN和IN算法则分别高出2.4和4.2个百分点. 因此, 本文改进算法Ours在ImageNet训练集上相对于BN算法和GN算法训练错误率并没有优势, 但是优于LN算法和IN算法.
图4和表1在训练集上的训练结果并不能说明一个模型的泛化能力, 一个模型即使训练拟合得很好, 其对于外来样本可能没有泛化性. 分析表2可知, 5个算法在ImageNet验证集错误率均高于在ImageNet训练集上的错误率. 对照组BN算法验证集错误率为28.6%, 相对于GN算法28.1%的错误率高出0.5个百分点, 而相对于本文改进算法Ours的28.3%错误率则高出0.3个百分点. 可以得出, 本文改进算法验证集上错误率在GN算法和BN算法之间, 略差于GN算法, 而优于BN算法. LN算法和IN算法的错误率相对于BN算法则分别高出4.6和5.1个百分点.
综上分析, 在本实验环境和条件下, 本文改进算法Ours相对于BN算法和GN算法有一定的竞争优势. Ours算法在训练集上表现不如BN算法和GN算法, 但是在验证集上则优于BN算法, 略差与GN算法. 即, 本文改进算法对外来样本处理得较好, 训练的模型泛化性能相对于BN算法有一定程度的提高. 由以上实验也可以得出, 采用LN算法和IN算法训练的ResNet网络虽然训练能够收敛, 但是训练集和验证集分类错误率都比较高. 这是因为LN算法主要用于RNN, 而IN算法主要用于图像风格化等, 都有其特定的适用场景, 其适用范围可能没有BN算法、GN算法以及本文改进算法Ours那么广.
4.2.3 目标检测和分割实验对比该组实验中, 本文验证改进算法在COCO2017数据集上目标检测和实例的效果. 实验采用深度学习框架caffe2, 以及通用目标检测框架Detectron, 目标检测算法使用Mask R-CNN.
表3列出了采用Mask R-CNN作目标检测和实例分割时, 以ResNet50的conv4作为目标的特征提取层, conv5层接一个ROI层用于目标分类和回归. 在该实验中, 改进算法比批规范化算法目标边框的APbbox值提高了0.5, 而掩膜的APmask值提高0.1. 该实验说明在目标检测和实例分割任务上, 一定程度上本文改进算法的目标检测泛化能力优于BN算法. 图6为采用本文改进算法后Mask R-CNN效果图.
| 表 3 Mask R-CNN目标检测与分割 |

|
图 6 Mask R-CNN效果图 |
4.2.4 鲁棒性说明
本文算法在神经网络模型训练过程中能够一定程度上提高基准网络模型的鲁棒性. 其中, 在VGG网络模型训练过程中尤为明显, 梯度弥散的现象出现的几率很小, 网络训练易于收敛. 基于大量对比实验以及分析得出:
(1) 本文算法在大批量数据训练过程中可以降低样本之间的关联性. 这种特性使模型易于训练.
(2) 鲁棒性的强弱很大程度依赖于基准网络. Su等[25]通过大量实验对18个常用的分类基准网络进行对抗样本研究分析发现: 1) 准确度越高的模型的普遍鲁棒性越差, 且分类错误率的对数和模型鲁棒性存在线性关系; 2) 相比于模型的大小, 模型的结构对于鲁棒性的影响更大; 3) 黑盒迁移攻击是一直以来都比较困难的任务, 但在VGG系列模型上生成的对抗样本可以比较容易地直接攻击其它的模型. 这在一定程度佐证了本文实验.
5 结束语深度神经网络模型的训练到目前为止还是非常具有挑战性的研究点. 本文在批规范化算法方面对其进行了探索. 在神经网络训练中, 改进算法有比较好的实验表现, 能够一定程度上提高分类精度, 在特定检测任务上提高检测精度. 但是, 该改进算法在模型训练前传过程中做了两次批规范化运算, 计算量增加不少, 因此, 深度神经网络模型的训练速度减慢了. 这是对时间与空间, 性能与速度的取舍平衡的考虑. 本课题将继续这两方面的研究.
| [1] |
Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [2] |
Deng J, Dong W, Socher R, et al. ImageNet: A large-scale hierarchical image database. Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami, FL, USA. 2009. 248–255.
|
| [3] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, NV, USA. 2012. 1097–1105.
|
| [4] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv: 1409.1556, 2014.
|
| [5] |
Szegedy C, Liu W, Jia YQ, et al. Going deeper with convolutions. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA. 2015. 1–9.
|
| [6] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. 2016. 770–778.
|
| [7] |
Huang G, Liu Z, van der Maaten L, et al. Densely connected convolutional networks. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA. 2017. 2261–2269.
|
| [8] |
Howard AG, Zhu ML, Chen B, et al. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv: 1704.04861, 2017.
|
| [9] |
Zhang XY, Zhou XY, Lin MX, et al. ShuffleNet: An extremely efficient convolutional neural network for mobile devices. arXiv: 1707.01083, 2017.
|
| [10] |
Ma NN, Zhang XY, Zheng HT, et al. ShuffleNet V2: Practical guidelines for efficient CNN architecture design. Proceedings of the 15th European Conference on Computer Vision. Munich, Germany. 2018. 122–138.
|
| [11] |
Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. International Conference on Learning Representations. arXiv: 1412.6572, 2015.
|
| [12] |
Akhtar N, Mian A. Threat of adversarial attacks on deep learning in computer vision: A survey. IEEE Access, 2018, 6: 14410-14430. DOI:10.1109/ACCESS.2018.2807385 |
| [13] |
LeCun YL, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [14] |
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proceedings of the 32nd International Conference on Machine Learning. Lille, France. 2015. 448–456.
|
| [15] |
Ren SQ, He KM, Girshick RB, et al. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. DOI:10.1109/TPAMI.2016.2577031 |
| [16] |
He KM, Gkioxari G, Dollár P, et al. Mask R-CNN. Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy. 2017. 2980–2988.
|
| [17] |
Ioffe S. Batch renormalization: Towards reducing minibatch dependence in batch-normalized models. Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, CA, USA. 2017. 1945–1953.
|
| [18] |
Ba JL, Kiros JR, Hinton GE. Layer normalization. arXiv: 1607.06450, 2016.
|
| [19] |
Ulyanov D, Vedaldi A, Lempitsky V. Instance normalization: The missing ingredient for fast stylization. arXiv: 1607.08022, 2017.
|
| [20] |
Luo P, Ren JM, Peng ZL, et al. Differentiable learning-to-normalize via switchable normalization. arXiv: 1806.10779, 2018.
|
| [21] |
Wu YX, He KM. Group normalization. arXiv: 1803.08494, 2018.
|
| [22] |
Sutskever I, Martens J, Dahl G, et al. On the importance of initialization and momentum in deep learning. Proceedings of the 30th International Conference on International Conference on Machine Learning. Atlanta, GA, USA. 2013. III-1139–III-1147.
|
| [23] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. The Journal of Machine Learning Research, 2011, 12: 2121-2159. |
| [24] |
He KM, Zhang XY, Ren SQ, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification. Proceedings of 2015 IEEE International Conference on Computer Vision (ICCV). IEEE Computer Society. Santiago, Chile. 2015. 1026–1034.
|
| [25] |
Su D, Zhang H, Chen HG, et al. Is robustness the cost of accuracy? -- A comprehensive study on the robustness of 18 deep image classification models. arXiv: 1808.01688, 2018.
|
 2020, Vol. 29
2020, Vol. 29


