近年来, 随着经济的日益快速发展, 人口数量的不断增加, 能源的消耗也在持续增长. 在这种形势下, 清洁能源逐渐进入了人们的视线, 天然气作为一种绿色清洁能源, 渐渐展现了优势^[1]. 中国的能源需求正在不断增长. 自2005年至2018年, 我国天然气年消费量从467.63亿m³增长到2800亿m³, 增长率达到498.76%. 天然气负荷预测是城市燃气系统的设计与调度的重要依据, 同时也是确定燃气工程项目中经济可行性的理论依据. 只有合理科学准确地预测城市燃气的负荷, 才能够提高经济运行效率、提高资源利用率, 提高城市空气质量.

目前, 负荷预测的相关研究在天然气领域的应用正在不断的改进和发展. 文献[2]建立了一种自适应模糊推理系统的神经网络, 可在复杂环境下进行天然气负荷预测. 文献[3]把天然气和温度模型进行结合, 推演出了不同温度条件下天然气的消耗分布, 通过利用某城市的历史温度和天然气负荷数据, 对天然气的日负荷量进行了预测. 文献[4]提出了一种具有可变结构的自适应智能灰色预测模型, 该模型可以根据实际数据的特征对模型参数进行自动优化, 并且通过实验证明该模型的预测精度优于传统灰色模型. 文献[5]通过对杭州市天然气负荷与气象因子之间的关系研究, 建立了支持向量机的预测模型, 将杭州市天然气负荷数据输入模型中, 对模型预测值和期望值进行比对. 文献[6]利用果蝇算法对支持向量机参数进行优化, 采用可K-means聚类算法对负荷序列做了离群点分析, 通过对预测数据和期望数据的误差分析对模型进行检验, 实验结果表明优化后的输出要优于单一的SVM方法.

综上所述, 目前对天然气负荷的预测并没有形成成熟的体系. 当前的研究大多使用基于神经网络或者SVM的预测方法, 存在以下普遍的缺陷: SVM对大规模的数据训练比较困难, 而负荷预测需要大量数据对模型进行训练; 传统的神经网络预测容易出现局部最优问题, 而且神经网络算法的收敛速度也慢, 使得算法效率低下. 因此, 本文提出了一种基于遗传算法优化小波神经网络的预测方法GA-WNNs (Genetic Algorithm-Wavelet Neural Network). 该方法使用遗传算法优化小波神经网络, 利用遗传算法的寻优全局性克服小波神经网络容易出现的局部极小、过早收敛问题, 提高了预测模型的准确性.

1 小波神经网络 1.1 小波理论

小波分析是从傅里叶分析演化而来的, 为时间序列提供多分辨率分析. 在信号处理相关领域经常会使用到傅里叶分析, 它可以对信号的成分进行分析, 同时也能将这些成分合成相应的信号. 但是, 它有一个严重的不足, 就是不能在时间序列上刻画信号的局部特性, 对于一些突变信号和非平稳信号效果不好. 使用小波去噪的方法能够改善傅里叶变换去噪的这个缺点^[7].

小波函数是通过母小波函数进行平移和伸缩变化得到的, 小波分析是将信号分解成小波函数的叠加. 小波变换指的是把一个基本的小波函数 $\psi (t)$ 平移b以后, 再在不同的尺度a下与待分析的信号 $x(t)$ 做内积.

${f_{x\left( {a,b} \right)}} = \frac{1}{{\sqrt a }}\int_{ - \infty }^\infty {x(t)} \psi \left( {\frac{{t - b}}{a}} \right)dt\;\;\;{\rm{a}} > {\rm{0}}$

(1)

式(1)等效的时域表达式为:

${f_{x\left( {a,b} \right)}} = \frac{1}{{\sqrt a }}\int_{ - \infty }^\infty {x(\omega )} \psi \left( {a\omega } \right)_e^{j\omega }dt\;\;\;{\rm{a}} > {\rm{0}}$

(2)

式中, a和 $b$ 是式中的参数, a代表平移因子, b是伸缩因子. 从上式中可以看出小波分析能够通过小波基函数的变换进而对信号的局部特征进行分析, 在二维情况下具有信号方向选择性能力.

1.2 小波神经网络结构

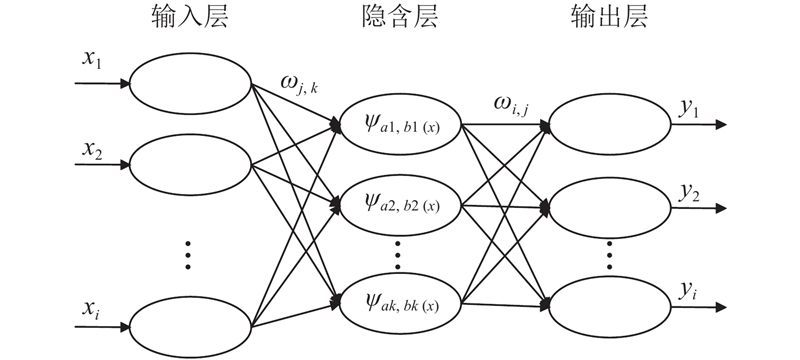
小波神经网络(WNN)模型是一种由小波分析和人工神经网络相结合的复杂模型. 它主要用于时间序列的预测. WNN模型的结构通常由以下部分组成: 离散小波分析, 小波系数重构, 人工神经网络预测和数据序列重构. 首先, 利用小波分解函数对时间序列进行离散小波分析, 提取出一系列高频和低频小波系数. 通过重新分解低频系列, 可以计算出任何比例的高频和低频小波系数. 其次, 利用小波重构函数, 重构了高频和低频小波系数. 通过分析重建的高频序列和低频序列, 可以粗略地检测时间序列的变化特征和趋势^[8]. 第三, 利用人工神经网络模型, 预测了高频和低频小波系数的重构序列. 其拓扑结构如图1所示.

图1中各个值代表的含义如下: ${X_1},{X_2},\cdots,{X_i}$ 表示输入数据; ${\omega _{j,k}}$ 代表输入层和隐含层之间的权值参数; ${\omega _{i,j}}$ 表示从隐含层到输出层之间的权值参数; ${y_1},{y_2},\cdots ,$ ${y_i}$ 表示输出层数据. ${\psi _{a,b}}\left( x \right)$ 代表小波函数, 本文采用的是Morlet函数, 该函数在时间与频率的局部化之间有很好的的平衡, 而且包含更多的振动信息, 表达式如下:

${\psi _{a,b}}\left( x \right) = \cos \left( {1.75x} \right)\exp \left( {\frac{{ - {x^2}}}{2}} \right)$

(3)

式中的a、b分别代表小波函数的平移因子和伸缩因子.

1.3 小波神经网络算法思想

为了使小波神经网络结构稳定, 需要借助数据对网络进行训练, 其次要借助测试数据集对训练好的网络进行验证. 算法步骤如下:

步骤1. 网络参数初始化. 随机初始化小波函数的平移因子、伸缩因子以及网络连接权重 ${\omega _{j,k}}$ , ${\omega _{i,j}}$ , 设置网络学习速率 $\eta $ .

步骤2. 数据分类. 将收集到的数据分成训练集和测试集两类, 将训练集数据输入到网络对模型进行训练, 测试集用来对训练好的网络进行精度测试.

步骤3. 预测输出. 通过输入数据对神经网络训练得到预测输出数据, 结合期望值和预测输出计算误差 $e$ .

步骤4. 参数修正. 根据上一步的误差不断调整网络权值和小波神经网络的参数, 使预测输出值与期望值的误差减小.

步骤5. 判断算法是否满足结束条件, 若不满足则返回步骤3.

小波神经网络采用梯度下降法修正网络的权值和小波函数的参数, 使得小波神经网络的预测输出值更加接近真实值. 对小波神经网络的修正步骤如下:

(1) 网络预测误差值

$e = \sum\limits_{k = 1}^m {yn(k) - y(k)} $

(4)

其中, $yn(k)$ 表示真实值, $y(k)$ 表示小波神经网络的预测输出值.

(2) 根据预测误差 $e$ 修正小波神经网络的权值和小波函数的参数

$\omega _{n,k}^{i + 1} = \omega _{n,k}^i + \Delta \omega _{n,k}^{i + 1}$

(5)

$a_k^{i + 1} = a_k^i + \Delta a_k^{i + 1}$

(6)

$b_k^{i + 1} = b_k^i + \Delta b_k^{i + 1}$

(7)

式中, $\Delta \omega _{n,k}^{i + 1},\Delta a_k^{i + 1},\Delta b_k^{i + 1}$ 是神经网络预测误差计算得出的, 计算公式如下:

$\Delta \omega _{n,k}^{i + 1} = - \eta \frac{{\partial e}}{{\partial \omega _{n,k}^i}}$

(8)

$\Delta a_k^{i + 1} = - \eta \frac{{\partial e}}{{\partial a_k^i}}$

(9)

$\Delta b_k^{i + 1} = - \eta \frac{{\partial e}}{{\partial b_k^i}}$

(10)

上式中 $\eta $ 为网络的学习速率.

2 遗传算法优化小波神经网络算法 2.1 遗传算法

遗传算法(Genetic Algorithms, GA)是由John Holland等人创建的著名进化算法. 在20世纪60年代, Rechenberg在一本名为“进化策略”的书中介绍了进化计算的理念. 继人工神经网络之后, 开始对遗传算法进行了初步的研究. 这两个领域都是受到生物系统的启发, 作为一种新型计算模型. 遗传算法是一种迭代算法, 具有高度并行、随机和自适应的特点, 可以在迭代过程中不断的改进解, 每个解称为一个染色体^[9]. 经过不断的循环遗传操作, 种群逐渐往好的方向进化, 最终得到最优解. 但是基本遗传算法存在收敛速度慢、易陷入局部极值等缺点, 导致小波神经网络的阈值以及网络连接权值未收敛至最优值. 本文采用的遗传算法是通过对选择算子进行改进, 在最优保存策略的基础上将每代种群按照计算的适应度值升序排序, 平均分成前中后三段, 并按照一定的比例进行选择. 从末段中随机选取个体补充由于选择操作而损失的个体, 这样既利用了最优保存策略的全局收敛特性同时也保持了种群的多样性^[10].

遗传算法中的遗传操作时算法的核心, 目的是通过逐代优化从而找到问题的最优解. 其中包括3个遗传操作: 选择, 交叉和变异^[11].

选择操作, 选择操作应用比较广泛的是比例选择操作和最优保存策略, 比例选择操作由于选择的随机性会存在误差, 但其简单实用仍被广泛实用. 本文采用了新的选择操作算法, 可以在种群中有效选择出较优的个体, 从而克服了最优保存策略只考虑保存种群中最优个体忽视了其余个体, 破坏种群多样性, 造成陷入局部极值.

交叉操作, 同生物界中染色体交叉相似, 染色体通过交换部分基因, 产生新的染色体.

变异操作, 是指种群中任意选取一个染色体, 选择染色体中的一点进行变异, 变异操作可以保持群体多样性, 防止早熟现象产生.

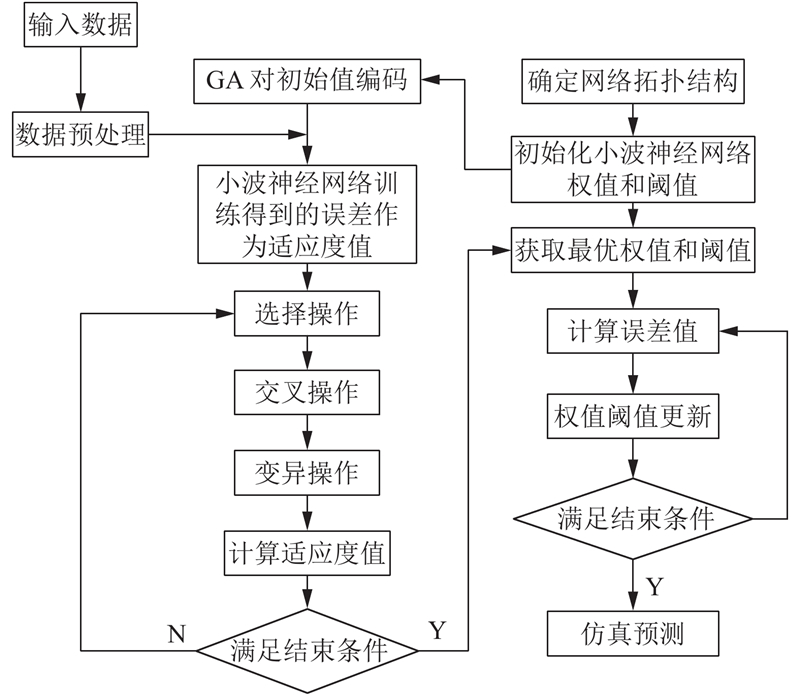
2.2 GA-WNN算法流程

通过使用遗传算法对神经网络的权值进行优化并且结合神经网络函数的较好的逼近能力, 可以对短期的天然气负荷量预测进行建模, 该算法克服了传统小波神经网络容易陷入局部最优的缺点. GA-WNN算法原理如图2所示.

基本的步骤如下:

步骤1. 设置种群大小为M, 随机生成初始种群N.

步骤2. 用步骤1中的种群N进行训练, 此时初始化获得小波神经网络平移因子和伸缩因子.

步骤3. 根据适应度函数计算个体的适应度值. 适应度值达到规定值直接到步骤6, 不满足进行下一步.

步骤4. 选择一部分适应度大的个体继承给下一代, 遗传操作后产生的适应度最低的个体由父代适应度值最大的个体代替.

步骤5. 将当前群体进行交叉变异操作, 生成新的种群, 转到步骤3.

步骤6. 结束循环, 将群体中的最优个体解码值作为小波神经网络的初始参数.

步骤7. 采用上述步骤获得最优参数进行建模.

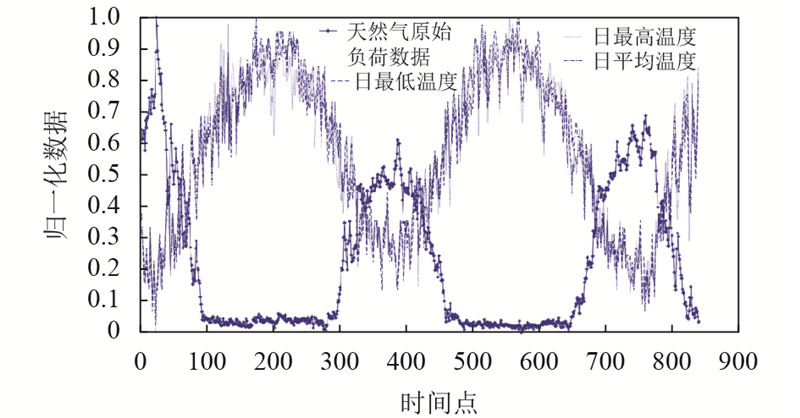
3 仿真实验 3.1 数据来源描述

通过SCADA数据采集系统采集了某市2016年1月1日到2018年4月19日共计840天的天然气日负荷量数据. 并通过当地气象局采集到每一天的日最高温度, 日最低温度, 日平均温度数据, 降雨量, 风速以及相对湿度的数据. 选取数据集共588条数据作为训练集, 剩余的252条数据作为测试集. 将收集到的数据通过Matlab绘制图如图3.

从图3可以看出天然气负荷量存在随机性与周期性变化规律, 而且负荷量的变化趋势与温度的变化趋势呈现出一定的相关性. 当温度较低时, 天然气负荷处于较高水平; 当温度较高时, 天然气负荷处于低水平. 天然气负荷变化随温度变化趋势明显, 所以温度是负荷预测的一个重要影响因素. 而降雨量, 风速以及相对湿度这3个数据通过Matlab绘制图像发现其变化规律与负荷量之间没有很直观的相关性, 为了进一步确认这3个因素对于天然气负荷影响程度, 本文进行了相关性系数的计算. 计算公式如下:

$r\left( {X,Y} \right){\rm{ = }}\frac{{Cov\left( {X,Y} \right)}}{{\sqrt {Var\left[ X \right] \times Var\left[ Y \right]} }}$

(11)

其中, $Cov\left( {X,Y} \right)$ 表示变量X和Y的协方差, $Var\left[ X \right]$ 表示变量X的方差, $Var\left[ Y \right]$ 表示变量Y的方差. 由式(11)我们可以计算得到天然气与各因素之间的相关性系数, 如表1给出.

由表1可以看出, 温度是影响负荷量的主要因素, 其他几项对于负荷量影响非常弱, 可以忽略不计.

通过企业调研以及对收集的数据分析发现, 城市燃气用户在平常日和节假日用气量有明显差异,所以要将这种差异考虑进去作为影响因素, 本文采用权重系数, 平常日权重系数为0.9, 节假日权重系数为0.3.

3.2 预测模型评价指标

为了评价GA-WNN算法的性能, 实验以传统BP神经网络、WNN神经网络、LSTM神经网络作为对比模型, 以决定系数(R²)、均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)作为评价指标. 计算公式如下:

${R^2}(y,\mathop y\limits^ \wedge ) = 1 - \frac{{\displaystyle\sum\nolimits_{i = 1}^n {{{({y_i} - {{\mathop y\limits^ \wedge }_i})}^2}} }}{{\displaystyle\sum\nolimits_{i = 1}^n {{{({y_i} - \mathop y\limits^ - )}^2}} }}$

(12)

$MSE(y,\mathop {{\rm{ }}y}\limits^ \wedge ) = \frac{1}{n}\sum\nolimits_{i = 1}^n {{{({y_i} - {{\mathop {{\rm{ }}y}\limits^ \wedge }_i})}^2}} $

(13)

$MAE(y,\mathop {{\rm{ }}y}\limits^ \wedge ) = \frac{1}{n}\sum\nolimits_{i = 1}^n {|{y_i} - {{\mathop {{\rm{ }}y}\limits^ \wedge }_i}|} $

(14)

$MAPE(y,\mathop {{\rm{ }}y}\limits^ \wedge ) = \frac{{\displaystyle\sum\nolimits_{i = 1}^n {\frac{{|{y_i} - {{\mathop {{\rm{ }}y}\limits^ \wedge }_i}|}}{{{y_i}}}*100} }}{n}$

(15)

式中, n为用来测试的天然气负荷样本, $\mathop y\limits^ - $ 为测试数据集的期望值, ${y_i}$ 为第i天的天然气负荷真实值, $\mathop {{y_i}}\limits^ \wedge $ 为第i天的天然气负荷量预测值.

3.3 实验及结果分析

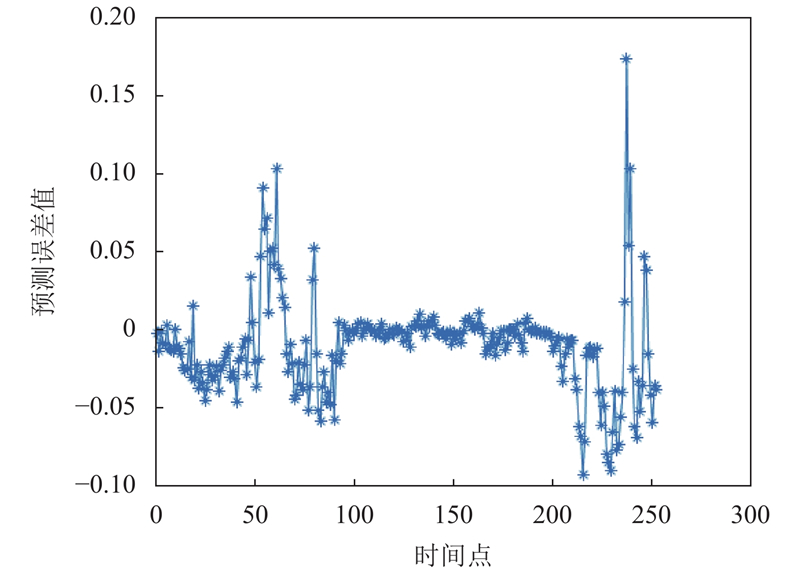
实验中遗传算法的迭代次数为200次, 交叉概率0.9, 个体数目为40个, 最大遗传代数设置为100. 神经网络模型参数设置, 学习率为0.05, 训练次数100次. 图4和图5是实验在Matlab环境下仿真结果, 表2为不同神经网络模型的各项评价指标.

由图4可知预测误差值波动在0.1到0.2之间, 图5绘制了不同预测模型的预测结果与GAWNN的对比, 通过图像我们不难看出虽然各个神经网络整体上都能反映出天然气日负荷量的变化趋势, 但是GAWNN的拟合效果明显优于其他几种预测模型. 如表2所示, GAWNN的R²值比其他项更接近1, 拟合度好, 参考价值高. 而其他几项误差评价指标GA-WNN均低于其他预测模型, 充分表明GA-WNN预测模型对短期天然气日负荷量有更高的预测精度. 通过Matlab实验证明, 未经优化的小波神经网络需要56次才能达到目标精度, 遗传算法优化后的小波神经网络仅需25次就达到了目标精度, 在总的运行时间上后者比前者减少9.467 102 s. 运行时间的减少一方面是由于改进选择操作后计算量相对减少, 另一方面改进以后的遗传算法搜索出较优的初始权值使得小波神经网络进一步寻找最优解节省时间. 将本文方法应用到不同地区门站进行预测都得到较好的预测结果.

综上所述, 本文提出的基于遗传算法优化小波神经网络的预测模型对于短期天然气负荷预测具有很好的预测精度, 且能够较好的反映出负荷量的趋势, 具有一定的工程应用价值.

4 结论

本文通过研究天然气负荷数据与每日温度之间的关系, 建立了小波神经网络预测模型, 并通过遗传算法对小波神经网络出现的易陷入局部最优以及收敛速度缓慢等问题进行改进. 通过与不同模型进行比对试验, 最后仿真结果表明, 经过遗传算法优化后的小波模型针对天然气负荷预测具有学习速率快, 有较强的逼近能力以及全局寻优等有点, 能够大大的提高燃气负荷预测的精度, 对燃气企业有较大的帮助.