随着客服中心服务量的不断增加, 如何保证在高峰时段和突发情况下有足够的客服人员在服务, 已成为一个越来越紧迫的问题. 实际上, 在线客服系统是不能够完全自动化完成客服中心的复杂调度和计划任务. 人的交互作用是客服中心必不可少的, 因此如何对客服中心的服务量进行预测, 对于保证客服中心提供的服务能够使客户获得较高的满意度是非常重要的[1].
目前, 对于服务量的预测方法已有多种, 如时间序列、排队论、回归预测和神经网络等. Andrews等[2]和Antipov等[3]提出了一种具有解释变量的自回归综合移动平均ARIMAX模型, 该模型使用如促销周期、广告响应和日历效应等外部变量. Aldor-Noiman等[4]提出了一种基于混合泊松过程方法的统计模型, 该模型考虑事件的影响, 例如将账单待出时期作为外部变量. Niu等[5]提出了一种特殊的回波状态网络, 在该网络中每个时间序列具有不同的存储层, 并且该网络将外部变量也考虑其中. ARIMAX模型和基于混合泊松过程方法的统计模型属于参数方法, 虽然可以明确各变量之间的数量关系, 定量分析变量对因变量的影响大小, 但是其方法内部参数的设定受使用者的主观影响较大, 不同的使用者很可能会得到相差很大的结果[6]; 回波状态网络属于非参数方法, 依靠数据来调节模型内部的参数, 进而得到变量与因变量之间的关系, 但是对于长时间序列, 其预测能力有限. 因此长短时记忆神经网络(LSTM)被提出, 它是一种改进的时间递归神经网络(RNN), 可以学习时间序列长短期信息. 由于其包含时间记忆单元, 因此适合处理和预测时间序列中的间隔和延迟事件. 但是LSTM仍然有2个缺点: 一是隐含层数和隐含层神经元数难确定; 二是学习率和迭代次数难确定[6]. 隐含层数和隐含层神经元数直接决定模型的拟合能力, 学习率和迭代次数影响模型的训练过程和效果. 在实际应用中, 这些参数都是依靠经验来确定, 具有较大的随机性, 这降低了模型的预测效果.
本文主要贡献和创新如下:
(1)提出了基于算法DMPSADE的一种改进算法IDMPSADE, 即通过反向引导寻优效果不佳的父代种群变异方向, 提升搜索全局最优能力.
(2)建立了IDMPSADE-LSTM预测模型, 并且分析了在线客服系统的系统历史服务量数据, 挖掘出关键影响因素, 将其作为LSTM的多输入变量, 利用IDMPSADE对LSTM的部分超参数进行寻优, 从而提升了IDMPSADE-LSTM预测模型的精确度.
本文内容安排如下: 第1节主要介绍已有的服务量预测方法. 第2节针对各预测方法存在的不足, 引入构建本文预测模型所需的背景知识. 第3节介绍改进的算法IDMPSADE, 并与多种其它差分进化算法进行实验对比. 第4节构建IDMPSADE-LSTM预测算法模型. 第5节通过分析历史数据, 选取服务量影响因素作为LSTM的多输入变量, 利用IDMPSADE-LSTM预测模型对服务量进行预测, 并且与其他神经网络以及混合预测模型进行实验对比分析. 第6节对IDMPSADE-LSTM预测模型进行总结.
1 相关知识 1.1 长短时记忆神经网络LSTM原理对于标准循环神经网络结构而言, 存在一个问题: 一般神经网络的信息从输入层到隐含层到输出层单向流动, 循环神经网络的信息传递存在定向的循环, 很容易出现梯度消失和梯度爆炸[7-9]. LSTM结构由一组循环连接的子网(称为记忆单元)组成. 每个记忆单元包含一个或多个自连接的记忆细胞和三种门(输入门、输出门和遗忘门), 这三种门允许记忆细胞存储访问长时间段的信息, 因此能够缓解梯度消失的问题[10]. LSTM中由单个记忆细胞构成的记忆单元如图1所示.
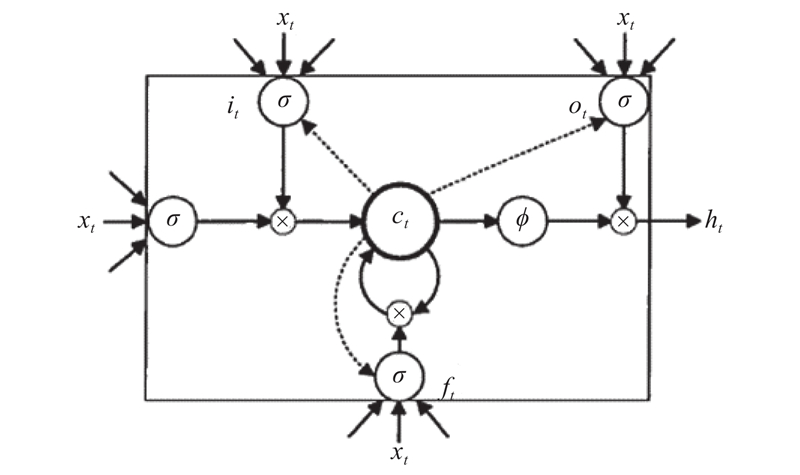
|
图 1 LSTM单细胞记忆单元示意图 |
某一时刻t的状态计算过程如下:
| ${g_t} = \phi \left( {{W_{xg}} \cdot \left[ {{x_t},{h_{t - 1}}} \right] + {b_g}} \right)$ | (1) |
| ${i_t} = \sigma \left( {{W_{xi}} \cdot \left[ {{x_t},{h_{t - 1}}} \right] + {b_i}} \right)$ | (2) |
| ${f_t} = \sigma \left( {{W_{xf}} \cdot \left[ {{x_t},{h_{t - 1}}} \right] + {b_f}} \right)$ | (3) |
| ${o_t} = \sigma \left( {{W_{xo}} \cdot \left[ {{x_t},{h_{t - 1}}} \right] + {b_o}} \right)$ | (4) |
| ${c_t} = {f_t} \odot {c_{t - 1}} + {i_t} \odot {g_t}$ | (5) |
| ${h_t} = {o_t} \odot {c_t}$ | (6) |
其中,
差分进化算法是一种针对种群演化的计算技术, 初衷是为了解决切比雪夫多项式问题, 在发展过程中, 研究人员发现它也可以用于解决复杂优化问题. 差分进化算法保留了基于种群的全局搜索策略, 采用实数编码, 变异操作采用个体间的差值与变异率相乘, 并且使用一对一的竞争生存策略, 从而降低简化遗传操作. 此外, 因为差分进化算法具备独特的记忆能力, 所以它可以根据跟踪到的动态搜索情况调整搜索策略, 全局收敛能力和健壮性相较其他进化算法优越. 虽然数学方法能够对很多抽象问题具象逻辑求解, 但是自然界中依旧存在大量利用常规的数学归纳方法无法解决的优化问题, 差分进化算法对此类问题无需其特征信息就能求解. 因此, 差分进化算法因其拥有的高效搜索能力对于学术研究和工程类应用而言存在一定的意义与价值[12].
1.2.2 DMPSADE算法流程差分进化算法的搜索能力是由被选择的变异策略和相关的控制参数决定, 所以选择适当的变异策略和控制参数对差分进化算法性能的改善是至关重要的, 基于离散变异控制参数的自适应差分进化算法(DMPSADE)核心是实现控制参数和变异策略的自适应, 同时确保每个变量的控制参数能够进行独立演化[13].
(1)初始化
| $x = {x_{\min }} + ({x_{\max }} - {x_{\min }}) \times { rand}(NP,D)$ | (7) |
(2)种群进化
变异操作: 对于每个个体
边界操作: 如果
交叉操作: 如式(8)所示, 其中
| $u_{ij}^{G + 1} = \left\{ {\begin{array}{*{20}{l}} {v_{ij}^{G + 1},{R_j} \le CR}\\ {x_{ij}^G,{R_j}>CR} \end{array}} \right.\!\!\!,j = 1,2, \cdots ,D$ | (8) |
选择操作: 如式(9)所示.
| $x_i^{G + 1} = \left\{ {\begin{array}{*{20}{c}} {u_i^{G + 1},f(u_i^{G + 1}) \le f(x_i^{G + 1})}\\ {x_i^{G + 1},f(u_i^{G + 1}) > f(x_i^{G + 1})} \end{array}} \right.\!\!\!\!,i = 1,2, \cdots ,NP$ | (9) |
(3)变异策略自适应
如果
如果
(4)控制参数自适应
由于迭代数G、上一代变异控制参数值与交叉控制参数值对下一代变异控制参数和交叉控制参数的更新有一定影响, 故以此为判断条件, 通过计算每个个体的权值, 获取每个个体的变异控制参数加权平均值与种群的交叉控制参数加权平均值, 利用正态分布函数对控制参数进行更新.
(5)迭代
种群迭代一次, 即
(6)评估
重复步骤(2)~(5)直到迭代数值达到最大值或评估函数收敛精度达到要求.
2 IDMPSADE算法DMPSADE算法主要思想是种群在经过初步的初始化、种群进化之后, 进行变异策略和控制参数的自适应行为, 然后选择评估值小的种群作为最佳种群. IDMPSADE以DMPSADE算法思想为基础, 初始化种群时均采用正向引导变异, 当正向引导的效果不佳即子代种群适应度函数大于父代种群适应度函数时, 此处的适应度函数为算法的寻优函数, 对父代种群个体进行反向引导, 即更改引导方向, 选择反向引导更为直观, 从而提高跳出局部最优和搜索到全局最优的可能性. 反向引导体现在改进策略公式的F参数符号中, 具体如式(10), 式(11)至式(14)所示.
DE/rand/1策略:
| $v_i^{G + 1} = x_{{r_1}}^G - F * (x_{{r_2}}^G - x_{{r_3}}^G)\;\;$ | (10) |
DE/rand/2策略:
| $v_i^{G + 1} = x_{{r_1}}^G - F * (x_{{r_2}}^G - x_{{r_3}}^G) - F * (x_{{r_4}}^G - x_{{r_5}}^G)$ | (11) |
DE/best/2策略:
| $v_i^{G + 1} = x_{best}^G - F * (x_{{r_1}}^G - x_{{r_2}}^G) - F * (x_{{r_3}}^G - x_{{r_4}}^G)$ | (12) |
DE/current-to-best/1策略:
| $v_i^{G + 1} = x_i^G - F * (x_{best}^G - x_i^G) - F * (x_{{r_1}}^G - x_{{r_2}}^G)$ | (13) |
DE/current-to-best/2策略:
| $v_i^{G + 1} = x_i^G - F * (x_{best}^G - x_i^G) - F * (x_{{r_1}}^G - x_{{r_2}}^G + x_{{r_3}}^G - x_{{r_4}}^G)$ | (14) |
IDMPSADE算法的控制参数包括变异控制参数与交叉控制参数, 参数的定义与DMPSADE算法的一致, 公式如式(15)至式(17)所示.
| $w_i^G = \frac{{\left| {f(u_i^{G + 1}) - {f_{\max }}\;} \right|\;}}{{\displaystyle\sum\limits_{i = 1}^{NP} {\left| {f(u_i^{G + 1}) - {f_{\max }}\;} \right|\;} }}$ | (15) |
| $F_{wj}^{G + 1} = \sum\limits_{i = 1}^{NP} {(w_i^G \times F_{ij}^G)} $ | (16) |
| $CR_w^{G + 1} = \sum\limits_{i = 1}^{NP} {(w_i^G \times CR_i^G)} $ | (17) |
当更新条件为
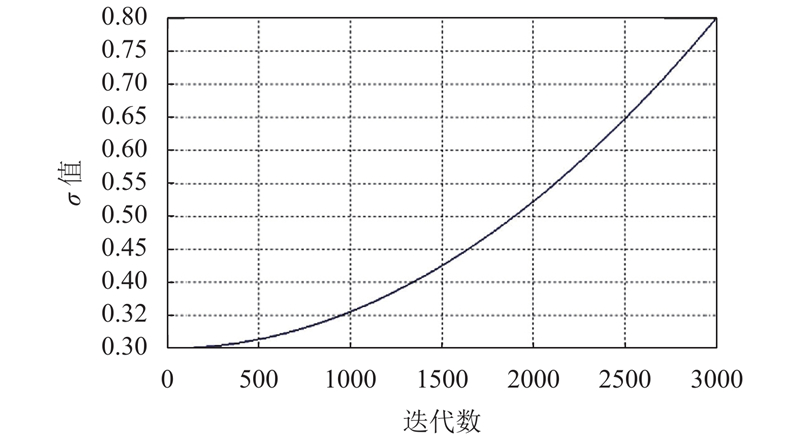
|
图 2 |
由于IDMPSADE算法的控制参数更新方式与DMPSADE算法相同, 故根据已有的实验分析[13]可知, 控制参数具有极大的随机性, 每个种群个体有其变异控制参数与交叉控制参数, 适应性在不同的测试函数上表现也不同.
为了测试IDMPSADE的寻优性能, 除选择DMPSADE算法进行实验对比, 还选择了jDE[15]和SaDE[16]在4种常用测试函数上进行测试, 这4种测试函数具有不同的特性, 可抽象地表示实际生活的不同问题. 测试函数分别为F1-Shifted Schwefel’s Problem 1.2 with Noise in Fitness, F2-Shifted Rosenbrock’s Function, F3-Non-Continuous Rotated Hybrid Composition Function, F4-Rotated Hybrid Composition Function without bound, 其中F1为单峰函数, F2为多峰函数且极值点个数较多, F3、F4为组合测试函数[17].
设置参数NP=100,
| 表 1 各差分进化算法标结果对比 |
3 IDMPSADE-LSTM预测模型
参数的选取对LSTM的预测效果存在较大影响. 采用IDMPSADE算法对LSTM参数进行优化, 需要进行寻优操作的主要参数有第一层隐藏层的神经元数
Step 1. 初始化. 将LSTM模型中的控制参数数目作为IDMPSADE算法的问题维度, 即D的取值; 将在线客服系统的服务量划分为训练LSTM的训练数据与预测数据. 选取LSTM的拟合值与真实值之间的RMSE作为目标函数. 初始化IDMPSADE算法的基本参数包括种群规模、最大迭代次数、变异参数和交叉参数. IDMPSADE模型的种群按照式(7)产生, 种群中的每个个体均是LSTM模型的一个参数组合.
Step 2. 种群进化. 首先判断是否达到迭代结束条件, 即全局极小值是否达到了设定的精度或者是否达到了设定的最大迭代次数. 如果是, 则停止迭代输出最优个体; 否则, 种群继续进行变异、边界和交叉操作得到下一代种群个体
Step 3. 控制参数自适应. 由于迭代数G、上一代变异控制参数值与交叉控制参数值对下一代变异控制参数和交叉控制参数的更新有一定影响, 根据种群个体目标函数值的分布差异性以及当前的迭代次数, 更新变异控制参数F与交叉控制参数CR, 转下一步.
Step 4. 更改变异方向. 如果下一代种群个体
Step 5. 迭代. 种群迭代一次, 即
Step 6. 得到LSTM最优参数组合以及在线客服系统服务量的预测结果.
4 实验结果分析 4.1 服务量影响因素选取服务量数据来自于某电力客服中心从2016年1月至2018年12月的数据中心记录, 包括每天各时间点的服务记录. 影响服务量的因素有很多. 由于在冬夏两季受温度影响, 居民用电量较多, 可能出现跳闸断电、电费相较过去有所增加等情况, 导致系统服务量变化较大. 雨雪天气影响居民的外出, 居民用电量较多, 可能出现电力设备故障、电费相较过去有所增加等情况, 导致系统服务量变化较大. 所以选取温度和降水量为主要影响因素.
在将温度和降水量作为LSTM的输入前, 需要对其进行相关性分析. 分析方法利用Pearson相关性分析和Spearman秩相关性分析[18]. 首先将近一年内的在线服务量按照工作日与非工作日划分, 同时对异常在线服务量进行数据清洗, 分别将温度、降水量作为第一变量, 将近一年的工作日在线服务量作为第二变量, 对第一、第二变量进行相关系数计算, 当Pearson相关度和Spearman相关度均大于0.5时, 说明影响因素与服务量的相关性强. 影响因素相关性分析结果如表2所示.
由计算结果得出, 温度和降水量这两类气象影响因素与在线服务量的相关性强, 并且温度和服务量的相关性高于降水量和服务量的相关性, 温度和降水量可作为LSTM预测系统服务量的输入.
| 表 2 影响因素相关性分析 |
4.2 服务量预测结果分析
(1) IDMPSADE参数与LSTM参数设置
种群规模NP为100, 最大迭代次数
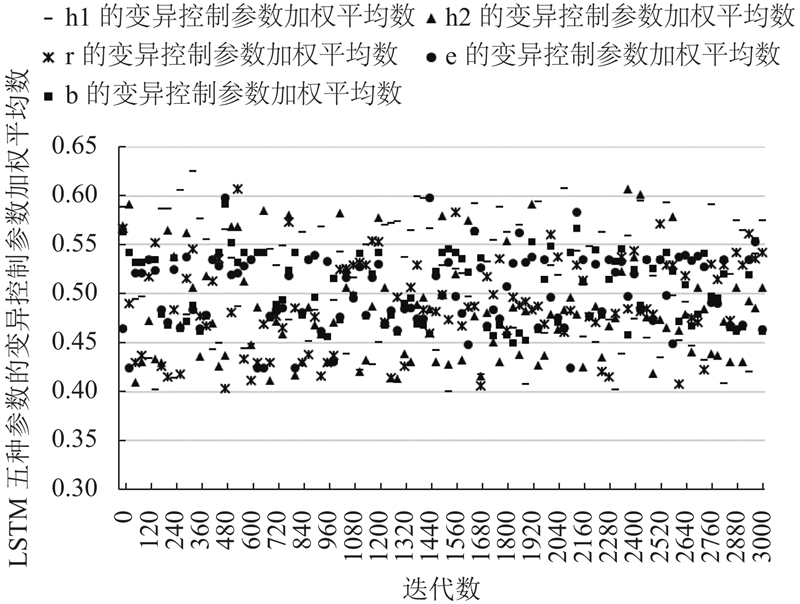
|
图 3 LSTM五种参数的变异控制参数F加权平均值 |
如图3与图4所示, 变异控制参数F的加权平均值在0.5上下浮动, 范围在0.4到0.65之间; 交叉控制参数CR的加权平均值在0.5上下浮动, 范围在0.4到0.6之间, 有效地平衡了算法的收敛精度与收敛速度.
(2)服务量预测精确度分析
基于统一测试数据集, 利用经过IDMPSADE算法优化后的LSTM神经网络对在线客服系统的服务量进行预测, 预测出代表336个小时内服务量的336个样本点数与原实际数据的对比如图4所示. 算法的预测性能指标选取均方误差MSE和平均绝对误差MAE, 如式(18)和式(19)所示.
| $MSE = \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} }}{n}$ | (18) |
| $MAE = \frac{{\displaystyle\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} }}{n}$ | (19) |
其中,
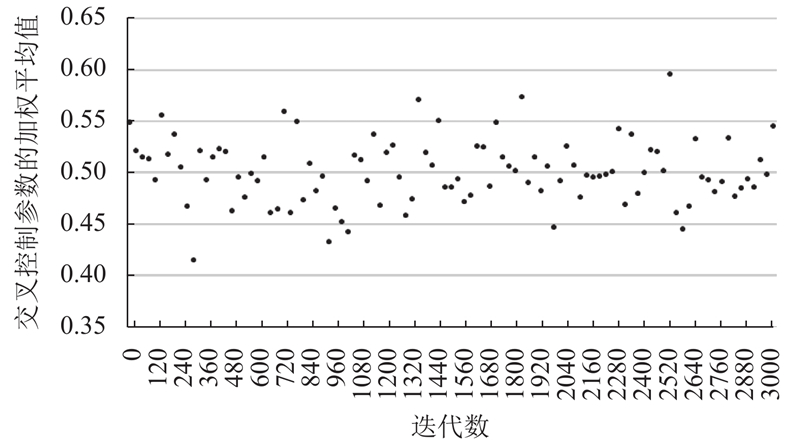
|
图 4 交叉控制参数CR加权平均值 |
采用传统的BP神经网络、RBF神经网络、SARIMA-SVM模型预测效果与IDMPADE-LSTM模型预测效果对比如表3所示.
| 表 3 不同模型预测结果对比 |
由图5可以看出, 在线客服系统的服务量具备一定的周期性, 预测结果相较实际数据的极值范围更小, 能够较好地预测出服务量的总体变化趋势, 有助于客服中心对客服提前排班以应对服务量变化情况.
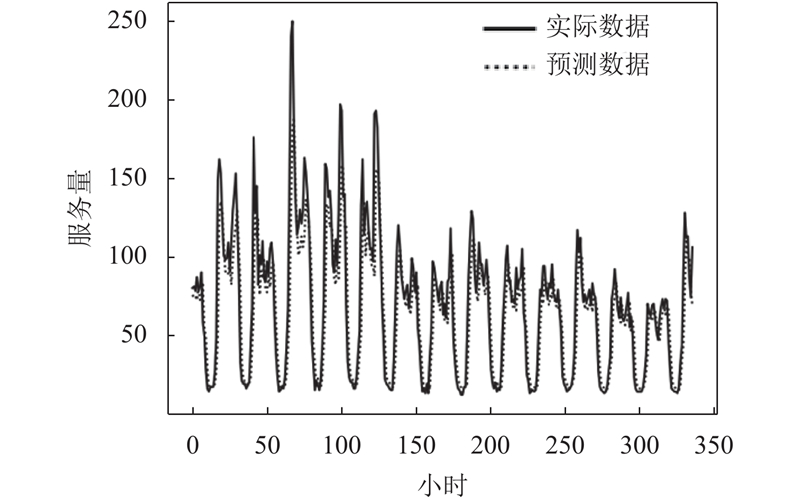
|
图 5 IDMPSADE-LSTM服务量预测结果 |
由表3可以看出, IDMPSADE-LSTM混合预测模型的预测误差小于BP神经网络、RBF神经网络以及SARIMA-SVM混合预测模型, 说明该服务量预测模型具有一定优越性, 预测精度有所提升.
5 总结系统服务量预测的准确性、有效性、实时性是公司为客服人员安排技能培训、进行工作规划的重要依据, 应用面向在线客服系统的服务量预测算法可为人力资源调度优化等工作提供科学的依据.
本文在对系统服务量数据调查分析的基础上, 提出了一种IDMPSADE-LSTM服务量预测模型, 与BP神经网络、RBF神经网络以及SARIMA-SVM混合预测模型相比, 本文提出的预测模型将关键影响因素与服务量自身的时间序列特征进行了有效的结合, 并且预测的精确度更高. 此外, 本文提出的IDMPSADE-LSTM预测模型解决了神经网络部分超参数的赋值随机性问题, 该模型除了可应用于系统服务量预测, 对于交通、金融等领域的相关数据预测也具备一定的参考价值.
| [1] |
Zhang J, Tian WF, Cui CY. Traffic forecasting of mobile communication in call center. Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology. Chengdu, China. 2010. 160–164.
|
| [2] |
Andrews BH, Cunningham SM. L. L. Bean improves call-center forecasting. Interfaces, 1995, 25(6): 1-13. DOI:10.1287/inte.25.6.1 |
| [3] |
Antipov A, Meade N. Forecasting call frequency at a financial services call centre. Journal of the Operational Research Society, 2002, 53(9): 953-960. DOI:10.1057/palgrave.jors.2601415 |
| [4] |
Aldor-Noiman S, Feigin PD, Mandelbaum A. Workload forecasting for a call center: Methodology and a case study. The Annals of Applied Statistics, 2009, 3(4): 1403-1447. DOI:10.1214/09-AOAS255 |
| [5] |
Niu DX, Ji L, Xing M, et al. Multi-variable echo state network optimized by Bayesian regulation for daily peak load forecasting. Journal of Networks, 2012, 7(11): 1790-1795. |
| [6] |
李万, 冯芬玲, 蒋琦玮. 改进粒子群算法优化LSTM神经网络的铁路客运量预测. 铁道科学与工程学报, 2018, 15(12): 3274-3280. |
| [7] |
Hochreiter S. Untersuchungen zu dynamischen neuronalen netzen[Master’s thesis]. Munchen: Technische Universität Münnchen, 1991.
|
| [8] |
Kolen JF, Kremer SC. Gradient flow in recurrent nets: The difficulty of learning longterm dependencies. In: Kolen JF, Kremer SC, eds. A Field Guide to Dynamical Recurrent Networks. New York: Wiley-IEEE Press, 2001. 237–243.
|
| [9] |
Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. DOI:10.1109/72.279181 |
| [10] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [11] |
孔德江. 面向序列数据的深度学习算法研究[博士学位论文]. 杭州: 浙江大学, 2019.
|
| [12] |
刘波, 王凌, 金以慧. 差分进化算法研究进展. 控制与决策, 2007, 22(7): 721-729. DOI:10.3321/j.issn:1001-0920.2007.07.001 |
| [13] |
Fan QQ, Yan XF. Self-adaptive differential evolution algorithm with discrete mutation control parameters. Expert Systems with Applications, 2015, 42(3): 1551-1572. DOI:10.1016/j.eswa.2014.09.046 |
| [14] |
呼忠权. 差分进化算法的优化及其应用研究[硕士学位论文]. 秦皇岛: 燕山大学, 2013.
|
| [15] |
Brest J, Greiner S, Boskovic B, et al. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-657. DOI:10.1109/TEVC.2006.872133 |
| [16] |
Qin AK, Huang VL, Suganthan PN. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. DOI:10.1109/TEVC.2008.927706 |
| [17] |
Suganthan PN, Hansen N, Liang JJ, et al. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. Singapore: Nanyang Technological University, 2005.
|
| [18] |
Xiao CW, Ye JQ, Esteves RM, et al. Using spearman’s correlation coefficients for exploratory data analysis on big dataset. Concurrency and Computation: Practice and Experience, 2016, 28(14): 3866-3878. DOI:10.1002/cpe.3745 |
 2020, Vol. 29
2020, Vol. 29


