1 引言

在传统的调度理论中, 通常工件的加工参数事先是完全确定的. 然而在现实生产过程中, 一些工件的实际加工时间会随其开始加工的时间的延后而增长. 这种情况经常发生在许多化学和冶金过程中. 例如, 在钢轧机中, 在轧制之前将锭加热至所需温度. 加热时间取决于锭的当前温度(这取决于锭等待的时间). 在等待期间, 晶锭冷却, 因此在炉中需要更多的加热时间. 这会导致被加工工件的处理时间的延长, 这种工件加工时间随开始加工时刻变化的现象称之为恶化效应.

本文研究的为带恶化的生产调度问题, 这个问题最早由Gupta等^[1]和Browne等^[2]提出, Gupta等^[1]在1988年引入了带恶化的单机调度问题, 他们认为任务的处理时间为多项式函数, 1990年Browne等^[2]提出工件的作业处理时间是不间断的, 是具有与开始时间相关的线性函数. 对于处理时间分段线性恶化的单机调度问题, Kunnathur和Gupta^[3]最早提出并给出了模型. Kubiak等^[4]比Kunnathur和Gupta^[3]多引入了恶化工期最大值H, 如果H趋近无穷大, 则恶化造成的增加量就是无限的, 否则增加量就是有限的. Hosseini和Farahani^[5]他们给定了一个规定的加工时刻h, 提前加工会得到一个奖励时间, 延后会有一定的恶化时间从而提出了新的分段恶化模型. Wang等^[6]考虑了非线性恶化的单机调度问题. Wei等^[7]和Wang等^[8]考虑了具有时间和资源相关处理时间的单机调度. Jiang等^[9], Wang^[10], Wang等^{[11, 12]}和Wang等^[13]考虑了具有学习效果和恶化工作的单机调度问题.

在带恶化并行机调度问题的求解方面, Rostami等^[14]考虑了模糊环境下带工件恶化和学习效应的异构并行机调度问题, 提出了分支定界算法以最小化提前延误和最大完工时间. Eduardo等^[15]考虑了带阶梯恶化工件的等同并行机调度, 以最小化总完工时间为目标函数, 提出了两种基于集合划分的数学模型. Bahalke等^[16]考虑了具有一般线性恶化效应和顺序依赖的调整时间的单机最大完工时间最小化调度问题, 并利用遗传算法进行求解. 国内对带恶化并行机调度的问题研究较少, 轩华等^[17]研究了以最小化最大完工时间为目标的不相关并行机环境下带恶化工件的车间调度问题, 假定工件在不同机器上有不同的恶化系数, 并设计了两段式编码的改进遗传算法. 郭鹏^[18]针对具有阶梯恶化效应的并行机调度问题, 构建了目标总完工时间最小化的混合整数规划模型, 并设计了基于工件排序的变领域搜索算法VNS.

就目前查阅的文献而言, 现有的研究大多假定工件具有固定的恶化率或者恶化效应为线性恶化以简化问题, 对分段线性恶化的并行机调度的研究还较少. 本文研究具有分段线性恶化的并行机调度问题, 其中工件加工时间 ${p_j} = {a_j} + {b_j}{x_{jb}}$ , ${a_j}$ 为工件j在正常情况下的基本加工时间, ${b_j}$ 为工件j的惩罚时间, ${x_{jb}}$ 为0-1变量, 如果工件j在恶化工期 ${h_j}$ 之前加工则 ${x_{jb}}{\rm{ = }}0$ , 否则发生恶化 ${x_{jb}}{\rm{ = 1}}$ .

2 问题描述

各参数符号定义如表1所示, 并给出以下问题假设:

(1)一台机器不能同时加工多个工件, 并且一个工件也不能被多次加工.

(2)工件没有优先权.

(3)机器是连续可用的, 即机器不会在有工件在等待加工时空闲.

(4)各工件正常情况下加工时间、恶化工期、恶化率已知.

基于以上假设, 问题即是对于n个在m台机器上加工, 已知正常情况下基本加工时间, 带有不同恶化工期和恶化率的工件, 寻找一个最优调度S, 使最大完工时间这一优化目标最小.

$ \begin{array}{l} {\rm{objective}}:\;\;\;\;\;\;\;\;\;\;MinZ = \displaystyle\sum\nolimits_j^n {{C_j}} \\ \;\;\;\;\;{\rm{s}}{\rm{.t.}} \end{array} $

(1)

${p_j} = {a_j} + {b_j}{x_{jb}},\forall j = 1,2,\cdots,n,{x_{jb}} \in 0,1$

(2)

$ \sum\nolimits_{k = 1}^m {\sum\nolimits_{l = 1}^n {x_{jk}^l \le 1,\forall j = 1,\cdots,n} } $

(3)

$ \sum\nolimits_{j = 1}^m {x_{jk}^l \le 1,\forall k = 1,\cdots,m,\forall l = 1,\cdots,n} $

(4)

$ S_k^l \ge C_k^{l - 1},\forall k = 1,\cdots,m $

(5)

$S_k^l \ge C_k^{l - 1},\forall k = 1,\cdots,m,\forall l = 2,\cdots,n$

(6)

$C_k^l \ge S_k^l + \sum\nolimits_{j = 1}^n {{p_j}x_{jk}^l,\forall k = 1,\cdots,m,\forall l = 1,\cdots,n} $

(7)

${C_j} \ge C_k^l - M(1 - x_{jk}^l),\forall j,l = 1,\cdots,n,\forall k = 1,\cdots,m$

(8)

${s_j} \ge S_k^l - M(1 - x_{jk}^l),\forall j,l = 1,\cdots,n,\forall k = 1,\cdots,m$

(9)

$x_{jk}^l \in \{ 0,1\} ,\forall j,l = 1,\cdots,n,\forall k = 1,\cdots,m$

(10)

$ S_k^l,C_k^l \ge 0,\forall k = 1,\cdots,m,\forall l = 1,\cdots,n $

(11)

其中, 式(1)是目标函数, 代表所需求的最小的最大完工时间, 也就是所需要求出的最优工件排序的最后一个工件的完工时间. 式(2)定义了工件的实际加工时间, 如果工件在恶化工期前加工, 那么加工时间为基本加工时间, 否则增加一个惩罚时间. 式(3)表示同一时间机器上只有一个工件在加工的. 式(4)表示机器同一个加工位置只能分配一个工件, 式(5)表示机器第一个的工件开始加工的时间非负. 式(6)表示机器上l位置工件的开工时刻是l–1位置的完工时间. 式(7)确定了机器k在l位置工件的完工时间. 式(8)和式(9)表示工件的完工时刻和开始加工的时间. 式(10)表示定义 $x_{jk}^l$ 为0–1变量. 式(11)表明机器位置l处工件开始加工的时刻和其完工时间是非负的.

3 混合进化算法设计 3.1 染色体编码及适应度函数

染色体编码用自然数序列表示工件加工的顺序, 解码时, 按照染色体编码的顺序依次将工件分配到最早可用的机器上. 适应度函数即计算对应染色体调度分配后的工件完工时间总和的倒数. 进化的目标是使适应度函数最大. 例如, 对于针对表2算例, 并以2台机器6个工件举例.

若某一染色体编码(根据SRF规则生成)为:

$ \begin{array}{*{20}{c}} 2&1&5&6&3&4 \end{array} $

则解码后甘特图如图1所示, 且总完工时间为617.

3.2 种群初始化

对立学习(Opposition-Based Learning, OBL)^[19]被应用于多种进化算法以提高性能, 在进化过程中, 不只考虑通常的解, 还考虑其对立解, 以提高收敛速度. 而在种群初始化过程中采用对立策略能够显著增强初始解的质量. 对立策略考虑当前点以及其对立点. 对立点的定义如下: 假设 $p({x_1},{x_2},\cdots,{x_n})$ 是N维空间的一个点, ${x_1},{x_2},\cdots,{x_n},x \in [{a_i},{b_i}],i = 1,2,\cdots,N$ , 则p的对立点可表示为 $\tilde p({\tilde x_1},{\tilde x_2},\cdots,{\tilde x_n})$ , 其中, ${\tilde x_i} = {a_i} + {b_i} - {x_i}$ . 计算随机生成的初始种群中每个个体的对立点并进行计较, 将两者中较好的解保留. 此外根据问题的性质, 基本加工时间较小的和惩罚时间较大的工件应先加工. 因此, 初始种群中的一个解可按照a_j/b_j的升序排列获得. 将其称为最小比率优先(Smallest Rate First, SRF)规则.

3.3 选择

采用轮盘赌选择方式, 若染色体 ${x_i}$ 应度值为 $f({x_i})$ 个体被选中的概率 $P({x_i}) = f({x_i})/\displaystyle\sum\nolimits_1^n {f({x_i})} $ , 即适应度越高的个体被选择的概率越大.

3.4 交叉

采用部分匹配交叉. 如两个父代个体为:

$\begin{array}{l} {\rm{p}}1\;\;\;\;1\;\;\;\;4\;\;\;\;5\;\;\;\;7\;\;\;\;2\;\;\;\;3\;\;\;\;6\;\;\;\;8\;\;\;\;9\\ {\rm{p}}2\;\;\;\;2\;\;\;\;1\;\;\;\;8\;\;\;\;3\;\;\;\;4\;\;\;\;5\;\;\;\;9\;\;\;\;6\;\;\;\;7 \end{array}$

随机选择两交叉点位并交换中间的染色体片段:

$ \begin{array}{*{20}{c}} {{\rm{p1}}}&1&4\\ {{\rm{p}}2}&2&1 \end{array}\left| {\begin{array}{*{20}{c}} 8&3&4&5\\ 5&7&2&3 \end{array}} \right|\begin{array}{*{20}{c}} 6&8&9\\ 9&6&7 \end{array} $

对于交叉点位外的区域出现的遍历重复, 根据匹配区域内的映射关系, 逐一进行交换. 比如, 对于p1交叉区域外重复的片段, 存在来自p2交叉区域内7到4, 2到8的映射. 即对p1匹配区外4和8分别以7和2替代. 对于p2同理.

即交叉后:

$ \begin{array}{*{20}{c}} {{\rm{p1}}}&1&7\\ {{\rm{p}}2}&8&1\; \end{array}\left|\; {\begin{array}{*{20}{c}} 8&3&4&5\\ 5&7&2&3 \end{array}} \right|\begin{array}{*{20}{c}} 6&2&9\\ 9&6&4 \end{array} $

3.5 变异

变异采用两点交换变异, 随机选择两交叉点并交换两基因点位. 如某个体p1为:

$ \begin{array}{*{20}{c}} {{\rm{p}}1}&1&4 \end{array}\;\left| {\;\begin{array}{*{20}{c}} 5&7&2&3&6 \end{array}\;} \right|\;\begin{array}{*{20}{c}} 8&9 \end{array} $

随机选择两交叉点位, 如p1中随机选择5工件与6工件, 变异后得到个体:

$ \begin{array}{*{20}{c}} {{\rm{p}}1}&1&4 \end{array}\;\left| {\;\begin{array}{*{20}{c}} 6&7&2&3&5 \end{array}\;} \right|\;\begin{array}{*{20}{c}} 8&9 \end{array} $

3.6 种群多样性

在遗传算法不断进行优化迭代的过程中, 在进化的初期, 种群拥有多种个体, 而后由于适者生存, 较高适应度的个体不断被保留, 种群的多样性不断下降, 逐渐趋于成熟, 遗传算法的择优基本依赖于种群中个体的变异, 此时遗传算法的搜索效率大大降低. 因此本文在提出遗传算法中加入种群多样性指标 ${N_p}$ 在种群多样性不足, 搜索效率不足时跳出遗传算法, 对目前得到的最优解进行变邻域搜索.

${N_t} = \frac{N}{{{N_p}}} \times 100\% $

其中, N是种群中基因完全不同的个体, 是种群规模.

3.7 变邻域搜索VNS

变邻域索算法(Variable Neighborhood Search, VNS)是1997年由Mladenovi和Hansen^[20]提出的一种局部搜索方法, 主要包括

随机扰动、局部搜索和邻域变换等3个过程.

本文采用5种邻域结构, 单点交换, 单点插入, 两点交换, 两点插入和逆序操作. 具体操作如下所示.

单点交换. 随机选取染色体序列上的两点进行交换.

单点插入. 随机选取染色体序列上一个基因, 将其取出, 插入到另外一个随机点位中.

两点交换. 首先随机选取染色体序列上的两个基因点, 再随机选择染色体上的另外两个基因点, 两次选择的基因点位上的基因进行互换.

两点插入. 随机取出染色体序列上的两个基因点, 将其分别插入两个随机点位.

逆序操作. 随机选择染色体上的两个基因点位, 将两个基因点位之间的基因全部逆序.

其中, 由于本文染色体解的形式为自然数序列, 其中单点交换与单点插入是所有邻域结构中对解产生的最微小的扰动, 保证了每次搜索的精度, 两点交换与两点插入是单点操作的延伸, 相当于同时进行两次单点操作但不评估首次交换后的结果, 一定程度上防止陷入局部最优. 逆序操作是为了进一步提升算法的性能加入的随机搜索过程, 在以上4个领域结构完成后实施.

3.8 搜索扰动

为防止算法陷入局部最优, 当算法连续多代没有改善时, 对当前的解进行扰动产生下一次迭代的初始解, 以减少重复搜索的时间. 本文采用3-opt交换算子, 具体实施过程为随机选择染色体上三个基因点位, 将染色体分成4段子序列, 保持子序列的方向不变对4段子序列重新进行连接, 易知4段子序列总共有4! =24种排列组合方式, 本算法仅交换中间两段子序列, 首位子序列保持不变. 例如某染色体为:

$ 10\;\;\;\;1\;\;\;\;4\;|\;6\;\;\;\;7\;|\;\;2\;\;\;\;3\;\;\;\;5\;|\;8\;\;\;\;9 $

随机选择4,7,5工件所在的位置, 交换中间两段子序列后得到:

$ \begin{array}{*{20}{c}} {10}&1&4&2&3&5&6&7&8&9 \end{array} $

3.9 混合进化算法流程

算法1. OBGAVNS

Input: 设置种群大小 $\scriptstyle{N_p}$ 的值, 最大迭代次数 $\scriptstyle{t_{\max }}$ 最大连续非改进迭代数 $\scriptstyle t_{\rm nip}^*$ , 设置种群多样度阈值 $\scriptstyle{N_{ t\min }}$ , 染色体编码长度n.

Step 1. 初始种群由 $\scriptstyle {N_p} - 1$ 个随机生成的个体以及一个由SRF规则生成的个体组成. 并根据 $\scriptstyle {N_p}$ 个个体生成其相应的对立种群.

Step 2. 使用适应度函数对初始种群所有 $\scriptstyle {N_p}$ 个体及其对立种群进行评估并比较种群中每一个原个体与其对立点的适应度值, 若对立点更优, 则替代原个体. 以此更新初始种群 $\scriptstyle P$ . 并记录最优个体 $\scriptstyle {X_{\rm best}}$ .

Step 3. 设代数t=1, 连续非改进迭代数 $\scriptstyle {t_{\rm nip}}$ =0;

Step 4. 当 $\scriptstyle {t_{\rm nip}} < t_{\rm nip}^*$ 时

Step 5. 轮盘赌选择适应度较高的个体, 将选出的个体放入育种种群 $\scriptstyle P'$ 中; /%选择操作%/

Step 6. 对种群 $\scriptstyle P'$ 中的每个个体, 按照一定的交叉概率 $\scriptstyle p_c$ 进行部分匹配交叉操作. /%交叉操作%/

Step 7. 对交叉操作后的每个个体, 以一定的变异概率 $\scriptstyle p_m$ 进行两点交换变异. /%突变操作%/

Step 8. 使用适应度函数计算育种种群 $\scriptstyle P'$ 的每个个体的适应度值, 将育种种群 $\scriptstyle P'$ 中个体全部插入到原种群中并淘汰适应度低的个体, 使种群中个体数目维持在 $\scriptstyle {N_p}$ . 若最优个体 $\scriptstyle {X_{\rm best}}$ 得到更新, 则 $\scriptstyle {t_{\rm nip}}$ =0, 否则 $\scriptstyle {t_{\rm nip}} = {t_{\rm nip}} + 1$ .

Step 9. 评估种群多样度 $\scriptstyle {N_t}$ , 若小于种群多样度阈值 $\scriptstyle {N_{t\min }}$ , 则跳出遗传算法循环进行VNS搜索, 否则回到Step 4.

VNS: 以最优个体 $\scriptstyle {X_{\rm best}}$ 作为初始解

Input最优个体 $\scriptstyle {X_{\rm best}}$ , 最大迭代次数 $\scriptstyle ite{r_{\max }}$ , 最大连续非改进迭代数 $\scriptstyle t_{\rm nip}^*$ .

Step 10. 令 $\scriptstyle iter = 0$ , $\scriptstyle {t_{\rm nip}} = 0$ .

Step 11. 进行N次单点交换邻域搜索, 每当邻域解有所改善, $\scriptstyle {t_{\rm nip}} = 0$ , 将邻域解视为当前解, 并重复此步骤. 若无改善 $\scriptstyle {t_{\rm nip}} = {t_{\rm nip}} + 1$ .

Step 12. 进行N次单点插入邻域搜索, 每当邻域解有所改善, $\scriptstyle {t_{\rm nip}} = 0$ , 将邻域解视为当前解, 并重复此步骤. 若无改善 $\scriptstyle {t_{\rm nip}} = {t_{\rm nip}} + 1$ .

Step 13. 进行N次两点交换邻域搜索, 每当邻域解有所改善, $\scriptstyle {t_{\rm nip}} = 0$ , 将邻域解视为当前解, 并重复此步骤. 若无改善 $\scriptstyle {t_{\rm nip}} = {t_{\rm nip}} + 1$ .

Step 14. 进行N次两点交换邻域搜索, 每当邻域解有所改善, $\scriptstyle {t_{\rm nip}} = 0$ , 将邻域解视为当前解, 并重复此步骤. 若无改善 $\scriptstyle {t_{\rm nip}} = {t_{\rm nip}} + 1$ .

Step 15. 进行N次逆序操作邻域搜索, 每当邻域解有所改善, $\scriptstyle {t_{\rm nip}} = 0$ , 将邻域解视为当前解, 并重复此步骤. 若无改善 $\scriptstyle {t_{\rm nip}} = {t_{\rm nip}} + 1$ . $\scriptstyle iter = iter + 1$

Step 16. 若 $\scriptstyle {t_{\rm nip}} > \frac{1}{2}t_{\rm nip}^*$ , 对当前解进行3-opt扰动, 并记录当前 $\scriptstyle {X_{\rm best}}$ .

Step 17. 若 $\scriptstyle {t_{\rm nip}} > t_{\rm nip}^*$ 或者 $\scriptstyle iter > ite{r_{\max }}$ , 结束VNS搜索, 否则回到Step 12记录此时 $\scriptstyle {X_{\rm best}}$ .

Out: 算法中的最佳个体X及其目标函数值.

4 算例仿真及结果分析

根据数学模型, 首先采用Gurobi对小规模算例进行计算, 验证所提出算法的有效性, 设定最大计算时间为1800 s. 此外, 为了验证所以出的算法性能, 同时在较大规模的算例中将其与传统GA算法以及VNS算法进行比较. 所有的算法均在处理器为Intel(R) Core(TM)i7-9750H CPU@2.60 GHZ, 内存8.00 GB微机Python 3.7上实现.

为了确定算法的参数, 根据文献[21]提供的各项参数进行取值设置.

小规模算例工件数 $n \in \{ 6,8,10,12\} $ 和机器数 $m \in $ $\{ 2,3) $ ;大规模算例工件数 $n \in \{ 30,50,100\} $ 和机器数 $m \in $ $\{ 5,10,20)$ .

算例中加工参数按以下规则随机产生:

基本加工时间为[1,100]之间均匀分布的随机数;

惩罚加工时间为[1,100]之间均匀分布的随机数;

恶化工期取来自不同区间 ${H_1}(0,{D_{0.5}}]$ , ${H_2}({D_{0.5}},D]$ , 和 ${H_3}(0,D]$ 的均匀分布的随机数, 其中 ${D_f} = \displaystyle\sum\nolimits_{i = 1}^{f \times n} {{a_i}/m}$ $ (0 \le f \le 1)$ .

传统GA算法参数设置: 种群规模 ${N_p} = 60$ , 最大连续非改进迭代数 $t_{\rm nip}^* = 60$ , 最大迭代次数 ${t_{\max }} = 1000$ , 交叉概率 $p_c = 0.65$ , 变异概率 $p_m = 0.01$ .

VNS算法参数设置: 取最大迭代次数 $ite{r_{\max }} = $ 200, 最大连续非改进迭代数 $t_{\rm nip}^* = 20$ . 初始解由最小比率优先(SRF)规则生成.

OBGAVNS算法参数设置: 为与传统GA算法以及VNS算法形成有效对照, 所采用的参数与对比参数大部分相同, 即种群规模 ${N_p} = 60$ , 最大连续非改进迭代数 $t_{\rm nip}^* = 60$ , 最大迭代次数 ${t_{\max }} = 1000$ , 交叉概率 $p_c = 0.65$ , 变异概率 $p_m = 0.01$ . VNS优化部分的最大迭代次数 $ite{r_{\max }} = 200$ , 最大连续非改进迭代数 $t_{\rm nip}^* = 20$ , 此外另取种群多样度阈值 ${N_{t\min }} = 0.05$ .

为了方便分析算法的性能, 本文将还目标值转化为相对百分比偏差(Relative Percentage Deviation, RPD)^[18], 以这个值作为参数分析的相应变量. RPD值由下式决定:

$RPD = \frac{{Z(A) - Z(B)}}{{Z(B)}} \times 100\% $

(12)

式(12)中Z(A)是算例计算目标值, Z(B)是算例在各种算法多次计算中所能获得的最优目标值.

小规模算例对比结果如表3所示, 表中数据均为计算10次后的平均值. 但由于Gurobi的性能限制, 随着算例规模的增大, Gurobi逐渐无法在设定的时间内求问题的解, 因此表中只列出Gurobi在设定时间内能求得解的算例. 同时将各算法在算例中得到的最小RPD值加粗.

根据小规模算例测试结果, 所采用来对比的OBGAVNS算法、传统GA算法以及VNS算法是有效的并且与Gurobi这类数学规划求解器相比, 在计算时间上具有明显的优势. 同时OBGAVNS算法的计算结果与VNS算法以及传统GA算法相比, 在大部分算例中都具有最小的RPD值, 其中OBGAVNS算法的平均RDP值为0.23%, 而VNS算法平均RPD值为0.53%, 传统GA算法平均RPD值为0.58%, 表现出较好的计算性能.

大规模算例如表4所示, 其中, RPDa为所用算法计算结果平均值的相对百分比偏差, RPDm为所用算法计算结果最小值的相对百分比偏差. 对表格中OBGAVNS算法在对比中最优部分进行加粗.

通过对比3种算法的RPD值可知, 所设计的OBGAVNS算法的所有算例的平均RDP值为0.36%, 最小RPD值为0.04%, VNS算法的平均RPD值为0.68%, 最小RPD值为0.21%, 传统GA的平均RPD值为3.37%, 最小RPD值为1.83%. 从所有算例的平均RPD值的计算结果看, OBGAVNS算法的计算性能效果优于传统GA与VNS. 此外, 在大部分的算例中, OBGAVNS算法在3种算法中都取得了最优的计算结果.

这是由于, 与VNS算法相比, OBGAVNS算法的VNS部分初始解由遗传算法提供, 其初始解质量优于一般的VNS算法. 此外, 与一般的VNS算法不同, OBGAVNS算法给VNS寻优部分提供的初始解带有一定的随机性, 在每次重复搜索中都会有所不同, 这为VNS算法提供了更大的搜索域, 此外在OBGAVNS算法中还加入了3-opt扰动算子能够使算法在VNS寻优部分能够跳出局部最优解.

随着算例规模的增加, 算法的计算时间也在同步增加, 所提出的OBGAVNS算法中由于有更多的操作算子, 因此较对比的算法而言需要更多的计算时间, 从大规模算例统计的结果看, OBGAVNS算法平均计算时间是3种算法中最长的, 传统GA时间最短, 这是由于传统GA虽然具有较好的全局搜索能力, 但欠缺局部搜索能力, 因此容易陷入局部最优过早收敛. OBGAVNS算法与VNS算法相比, 除了初始解生成多花费的时间外, 花费的时间主要是在扰动部分, 每次扰动后都需要花费额外的一部分时间进行寻优, 但与算法性能的提升来说, 仍在可接受的范围内, 并且随算例规模的增加, 计算时间的百分比差距也有所减少. 例如, S₁算例中5台机器30个工件OBGAVNS算法计算时间为VNS算法的5.52倍, 而增加到5台机器100个工件时计算时间缩短为2.97倍.

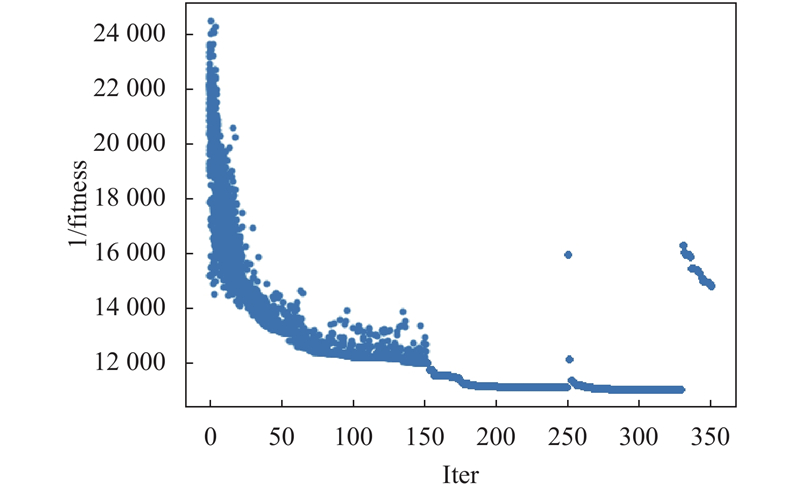
为了更直观的展示算法的性能, 以算例H1区间5台机器50个工件为例给出迭代中的个体分布图如2所示. 根据程序计算结果, 其中0到152代为遗传算法部分, 个体数为种大小, 在152代由于到达种群多样性指标阈值因而进入变邻域搜索部分, 对单一个体进行VNS优化, 并在连续非改进次数达到 $\dfrac{1}{2}t_{\rm nip}^*$ 时进行3-opt扰动(在图2中表现为适应度值变差), 开始重新搜索如此循环, 最终到达设定的最大迭代次数或连续非改进次数停止搜索, 输出迭代中最好的解.

5 结论与展望

本文针对具有线性恶化的并行机调度问题, 提出了一种混合进化算法OBGAVNS, 该算法采用工件序号编码以及机器先空闲先分配的解码规则, 用对立策略以及最小比率优先规则生成初始种群以提高初始种群的质量, 并且引入种群多样度指标加快算法的收敛; 针对遗传算法局部搜索能力不强的特点, 加入带有3-opt扰动算子的VNS变邻域搜索算法对遗传算法得到的结果进行优化. 通过对不同规模的算例进行仿真实验, 结果表明了所提出OBGAVNS算法的有效性, 并且其性能较传统GA与VNS算法均有所提升. 接下来的研究工作将考虑更复杂的机器环境, 如异速并行机、流水车间等, 并添加考虑能耗与调整时间等约束使之更贴近生产实际.