2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
中尺度涡是指空间尺度约为几十至几百公里、时间尺度约为几天至几个月的海洋涡旋, 携带着全球海洋的绝大多数能量, 在海洋的动能运输、热盐运输、化学物质运输以及营养物质运输中起到重要作用[1], 同时影响着全球气候变化和渔业等商业活动[2], 对人类活动和海洋科学都有着重要意义.
海洋物理上多利用卫星测高数据对中尺度涡进行检测, 但是对卫星数据的计算与处理通常依赖于由专家预定义或调整的参数[3-5], 参数的选取直接影响着中尺度涡识别的精准度, 且不同区域选取的参数不尽相同. 由于中尺度涡具有复杂的动态变化的特征, 对涡旋特征的检测需要逐点扫描, 再进行后续筛选, 耗时较长. 而海洋资料数量庞大, 分辨率越来越高. 通过逐点扫描和计算的方式要花费太多时间, 影响了对涡旋的进一步分析. 另外, 涡旋研究信息涉及到许多维度和变量, 以文字、图表为主. 对其进行对比和分析有相当多的工作量, 且不能较好地对海洋涡旋的空间位置、每个涡旋自身特征进行可视化展示. 涡旋检测速度的提升和涡旋信息可视化系统的开发可以在很大程度上提高对涡旋研究工作的效率.
为此, 本文提出了基于深度学习多目标检测的中尺度涡识别算法, 避免了阈值选取对涡旋检测的影响, 大大提升了涡旋检测速度. 同时设计可视化系统进行中尺度涡多维度展示, 并对涡旋的统计信息、特征分布和属性关联进行了洞察、说明和相关性分析.
本文的主要贡献如下:
(1) 提出一种基于深度学习的海洋中尺度涡旋检测算法, 可较准确、全面的检测中尺度涡, 并大大提升了检测速度;
(2) 设计中尺度涡时空特征及海洋信息协同可视化系统, 通过多视图联动及交互操作对中尺度涡信息进行多维展示;
(3) 利用可视化系统在个数和尺度统计、特征分布、属性关联等方面对中尺度涡进行细节性分析.
1 国内外研究现状海洋物理中对中尺度涡的识别算法大致可分为两类: 一是基于物理参数的方法, 其中Okubo-Weiss(OW)参数法[4, 5]应用最为广泛. 但其需要引入阈值
此外, Ashkezari等[8]将机器学习与涡旋检测结合, 构建涡旋相位角特征矩阵, 利用SVM算法进行分类训练, 最后使用固定大小的滑动窗格进行涡旋检测. Franz等[9]将卷积神经网络引入涡旋检测, 但其使用OW参数法提取涡旋特征构建训练集, 阈值选取的影响使其只能识别到特征非常明显的涡旋, 漏识别现象较严重. 以上两种方法均需先对涡旋类别学习, 之后使用滑动窗格扫描全局数据才能获取涡旋位置信息, 涡旋的识别和定位需分步进行.
目标检测是机器视觉中最常见的问题, 其中基于深度学习的YOLOv3算法[9]表现突出, 可以学习图像的全局信息, 直接输出目标类别和相应的定位, 并且大大提高了对小目标和紧凑密集或者高度重叠目标的检测, 非常适合在卫星高度计数据中有着小尺寸、高密度特点的中尺度涡的检测.
本文首次利用深度学习多目标检测网络进行涡旋识别, 避免了构建特征矩阵以及对全部数据扫描的工作, 对涡旋的识别和定位实现一步到位, 并且得到较好的检测结果, 大大提高了涡旋检测速度. 之后, 利用涡旋检测结果搭建中尺度涡时空特征及海洋信息协同可视化系统, 对中尺度涡的特征分布、多维度统计信息、属性关联, 以及对海洋属性的影响进行交互可视化展示, 可帮助用户查看涡旋各个维度下的信息及时空变化规律, 对比分析涡旋的特征和影响, 满足对涡旋和海洋信息进行直观性说明的需求, 大大减少研究人员对繁杂数据的对比、分析、统计工作.
2 海洋中尺度涡识别算法 2.1 算法概述海洋物理中对中尺度涡的检测通常需要设定阈值以分离中尺度涡涡核与海洋背景场, 阈值的设置直接影响着中尺度涡检测的准确度, 且不同区域的阈值不尽相同; 也可利用几何特征进行涡旋检测, 需要逐点扫描卫星高度计数据, 对疑似涡核点再作进一步判断, 但是随着卫星高度计数据量的增长、数据空间和时间精度的提高, 扫描任务的数据量成倍增加, 涡旋检测速度太慢会影响下一步对涡旋特征和影响的研究, 涡旋检测耗时太长也成为了亟待解决的问题.
本文算法首先将海面高度异常融合数据制作为单通道图像, 利用海面高度异常闭合等值线法对研究区域进行涡旋检测, 完成原始样本集的制作. 其次, 调整YOLOv3网络参数, 通过K-Means对样本标注框维度聚类得到先验框, 使得YOLOv3更适合对本文样本集特征的学习, 利用YOLOv3训练结果完成对测试集的涡旋检测并对检测结果进行处理和精准定位. 本文算法对涡旋检测有较高的准确率和召回率, 大大提高了涡旋检测速度, 并摆脱了阈值选取对涡旋检测的影响.
2.2 样本集的制作样本集包括图片集和标签集, 其中图片集为包含了涡旋特征的SLA图片, 作为YOLOv3的输入来源; 标签集为每张图片所包含的涡旋位置信息和类别信息.
2.2.1 样本集图片SLA数据覆盖全球, 包含海洋和陆地两部分, 其中陆地部分的数值设为−2147 483 647, 为了便于SLA数据与图片的转换, 本文首先将陆地部分的数值均设为0; 由于SLA数据的精度为0.0001, 数据范围为(–9.9999, 9.9999), 若直接转换为图片会造成严重的精度损失, 因此本文通过式(1), 将SLA数据转为正整数; 最后, 将处理后的SLA数据转换为16位单通道的tiff格式图片. 图1为生成的SLA灰度图像, 其中灰度为0的部分为陆地, 其余部分为海洋, 海洋部分不同程度的灰度变化即为海面高度的起伏.
| $SLA' = 10000 SLA + 10000$ | (1) |

|
图 1 海面高度异常灰度示意图 |
2.2.2 样本集标签
本文利用海面高度异常闭合等值线法对中尺度涡进行检测以制作样本集标签. 中尺度涡最直观的表现为闭合的海面高度异常等值线, 本文利用该特征具体使用的特征提取方法如下:
(1) 在气旋涡(反气旋涡)区域内有一个SLA局部最小(大)值.
(2) 涡旋外围要有闭合的SLA等值线.
(3) 气旋涡(反气旋涡)内所有网格点的SLA值都比边界SLA值要小(大).
(4) 涡旋振幅不小于3 cm.
由于SLA数据的分辨率为0.25°(约为27.75 km), 因此本文舍弃半径小于27 km的涡旋. 针对位于研究区域边缘的涡旋, 如果该涡旋所占区域超出研究区域边界, 则舍弃. 通过上述涡旋检测方法识别出的涡旋将根据涡核位置及半径信息, 通过式(2)至式(5)计算涡旋
| ${y_{\min }} = \left\lceil {{y_0} - R/27.75} \right\rceil $ | (2) |
| ${y_{\max }} = \left\lceil {{y_0} + R/27.75} \right\rceil $ | (3) |
| ${x_{\min }} = \left\lceil {{x_0} - R/27.75*\cos (lat)} \right\rceil $ | (4) |
| ${x_{\max }} = \left\lceil {{x_0} + R/27.75*\cos (lat)} \right\rceil $ | (5) |
由于涡旋特征尺度小, 分布密集, 且有不同参数的强弱划分, 将YOLOv3这种适用于自然图像的目标检测模型直接应用会存在以下问题:
(1) 在样本集标签制作中, 设定涡旋特征阈值va, 只提取特征值大于va的涡旋, 在训练中发现YOLOv3还会识别出某些特征值小于va的强度较弱的涡旋.
(2) 部分漏识别涡旋聚集于样本区域的边缘处.
针对以上问题, 本文对YOLOv3初次检测结果进行以下处理:
(1)筛选出YOLOv3识别的弱涡旋, 不作为本文对识别结果评判的计算.
(2)针对图片边缘涡旋的漏识别, 本文将研究区域在东、西、南、北四个方向分别平移至与样本区域重合度为70%处, 得到4个新区域, 位于样本区域边缘的涡旋在新区域中将位于中央位置. 使用YOLOv3训练结果分别对4个新区域进行涡旋检测, 并将识别结果重新偏移到原样本区域, 与初次识别结果叠加, 完成再识别.
2.3.2 识别结果处理由于再识别过程对同一局部区域有多次检测, 将会出现许多重复识别结果. 此外, YOLOv3的涡旋检测结果可以大体定位涡旋位置范围, 但是会存在位置和半径的偏差. 为了实现中尺度涡的精准定位以及相关属性的计算, 并且提高计算速度, 本文首先利用式(6)计算预测框的
| $IOU = are{a_{\rm overlap}}/are{a_{\min }}$ | (6) |
其中,
本文使用目标检测中常用的评价指标: 精确率(precision), 召回率(recall)对训练结果进行测评. 各评价指标的计算公式如式(7)、式(8)所示.
| $precision = \frac{{tp}}{{tp + fp}} = \frac{{tp}}{n}$ | (7) |
| $recall = \frac{{tp}}{{tp + fn}}$ | (8) |
其中,
本文提出的中尺度涡时空特征及海洋信息协同可视化系统, 通过多个版块的关联, 对中尺度涡的位置分布、直观特征、多维度统计信息、属性关联, 以及对海洋属性的影响进行交互可视化展示, 展示信息丰富, 交互操作多样, 可以使用户从时间、空间不同角度直观地分析涡旋分布特点、各属性特征, 以及与海洋环境的联系, 实现对涡旋及海洋特征的直观说明, 大大减少了涡旋研究者对各类涡旋及海洋数据对比分析的工作量. 本系统主要满足的需求如下:
(1)查看任意一天涡旋相关信息;
(2)对(反)气旋涡以及涡旋总体情况分类查看;
(3)查看涡旋个数统计、尺度统计和分布信息;
(4)查看涡旋自身特征及分布信息;
(5)查看涡旋各个属性信息查看及属性间的联系.
3.2 可视化数据及属性介绍本文可视化的相关属性定义如下:
(1)涡旋半径R
中尺度涡形状不规则, 本文取涡旋中心与8个邻域方向最外围的地理距离的平均值作为中尺度涡的半径R, 如式(9)所示.
| $R = ({r_{\text{东}}} + {r_{\text{西}}} + {r_{\text{南}}} + {r_{\text{北}}} + \frac{{{r_{\text{东北}}}}}{{\sqrt 2 }}{\rm{ + }}\frac{{{r_{\text{东南}}}}}{{\sqrt 2 }}{\rm{ + }}\frac{{{r_{\text{西北}}}}}{{\sqrt 2 }} + \frac{{{r_{\text{西南}}}}}{{\sqrt 2 }})/8$ | (9) |
(2)振幅A
中尺度涡的振幅定义为涡核与涡旋最外围等值线的SLA差值的绝对值, 如式(10)所示.
| $A = |SL{A_{\text{中心}}} - SL{A_{\text{最外围}}}|$ | (10) |
(3)涡度
涡度为速度场的旋度, 涡度值的大小代表着中尺度涡的强弱, 计算公式如式(11)所示.
| $\zeta = \frac{{\partial (v')}}{{\partial x}} - \frac{{\partial (u')}}{{\partial y}}$ | (11) |
其中,
| $u' = - \frac{g}{f}\frac{{\partial (SLA)}}{{\partial y}}$ | (12) |
| $v' = \frac{g}{f}\frac{{\partial (SLA)}}{{\partial x}}$ | (13) |
| ${\zeta _{rms}} = \sqrt {\frac{1}{N}\sum\limits_{t = 1}^N {\mathop \zeta \nolimits_t^2 } } $ | (14) |
(4)海洋动能EKE(Eddy Kinetic Energy)
中尺度涡活动较强的海洋区域一般具有较大的动能, 在地转假设条件下的计算如式(15)所示.
| $EKE = \frac{1}{2}(\mathop {u'}\nolimits^2 + \mathop {v'}\nolimits^2 )$ | (15) |
另外, 系统使用的逐日海表面温度(Sea Surface Temperature, SST)数据由California地球卫星微波遥感科研机构Remote Sensing Systems (RSS)提供, 分辨率为0.25°×0.25°.
3.3 可视化系统设计本文设计的中尺度涡时空特征及海洋信息协同可视化系统共包含涡旋特征统计、等值面特征、属性关联分析3类视图, 共5个版块. 各个版块通过时间选择联动变换, 展示同一天内不同维度下海洋与涡旋的不同信息.
3.3.1 涡旋特征统计视图涡旋特征统计视图对涡旋个数按时间进行统计, 对涡旋半径、振幅按尺度进行统计, 共分为2个版块.
(1)涡旋个数统计图
如图2所示, 在时间上以天和月为单位分别统计了涡旋个数, 用户可点选按钮分别查看; 在类别上以气旋涡、反气旋涡和全部涡旋统计个数, 由于反气旋涡对应SLA正异常, 气旋涡对应SLA负异常, 因此将反气旋涡、气旋涡个数的y坐标轴分别设计为正、负两个方向进行显示, 全部涡旋个数以折线形式展示. 用户通过选择日期可显示当前日期及之后30天的涡旋个数信息, 也可通过范围选择器同时查看更多日期的涡旋个数. 在涡旋个数月统计图中, 用户点击条形图可使系统界面显示当月第一天的涡旋信息. 通过鼠标交互, 用户可得到具体的涡旋数量, 增强了图表的可读性; 通过横向比较柱状图高度变化可得到涡旋数量的极值月份和变化趋势.

|
图 2 涡旋个数统计图 |
(2)涡旋尺度折线图
如图3所示, 根据涡旋的半径和振幅尺度进行统计, 由于SLA数据的分辨率为0.25°×0.25°, 对于涡旋半径的计算只能精确到约27.75 km. 因此, 将半径以26 km为刻度单位进行均分, 振幅以1 cm为刻度单位进行均分. 折线图中标出不同尺度下分布最多的涡旋个数, 方便查看涡旋的主要尺度范围.
3.3.2 等值面特征视图如图4所示, 等值面特征视图中使用专业气象数据处理语言NCL (NCAR Command Language)将海平面高度异常数据、海洋涡度值、海洋动能值绘制等值面图, 并将中尺度涡识别结果根据半径尺寸和极性在等值面图上进行标注, 红色圆圈为反气旋涡, 蓝色圆圈为气旋涡. 用户可点选按钮查看不同类别的等值面图, 可清晰地看到每日的涡旋特征分布, 同时对涡旋与海洋涡度、海洋动能的联系有形象的认识.

|
图 3 涡旋尺度折线图 |

|
图 4 等值面特征图 |
3.3.3 属性关联分析视图
属性关联分析视图利用相关属性制作平行坐标系, 由于海洋和涡旋的属性在不同纬度上具有明显差异, 本视图还以纬度为单位对涡旋属性进行统计, 并绘制热力图分析海洋属性的空间差异. 共分为2个版块.
(1)涡旋海洋关联属性平行坐标系
如图5所示, 根据涡旋半径、振幅、涡度均方根、涡动能以及涡旋中心海表温度5个属性构建平行坐标系, 按颜色划分涡旋极性. 用户可得到当日涡旋各属性的尺度范围, 并可通过框选查看某范围下任意属性的特点, 滑动选择框, 可以看到某一属性的变化对其它属性的影响或属性间存在的联系, 从而进一步分析涡旋对海洋的影响.
(2)涡旋属性空间统计与海洋动能热力图
如图6所示, 将研究区域的海洋动能以经纬度1°×1°的分辨率进行统计, 绘制热力图; 同时, 以1°纬度为单位对涡旋半径、振幅、出现频率进行统计绘制折线图, 二者共用同一y轴. 通过点选不同的属性并选择不同时间段进行查看, 可明显对比得出涡旋尺度、出现频率在不同纬度下的差异, 以及海洋动能的强弱分布规律, 涡旋的不同属性对海洋动能的影响也一目了然.
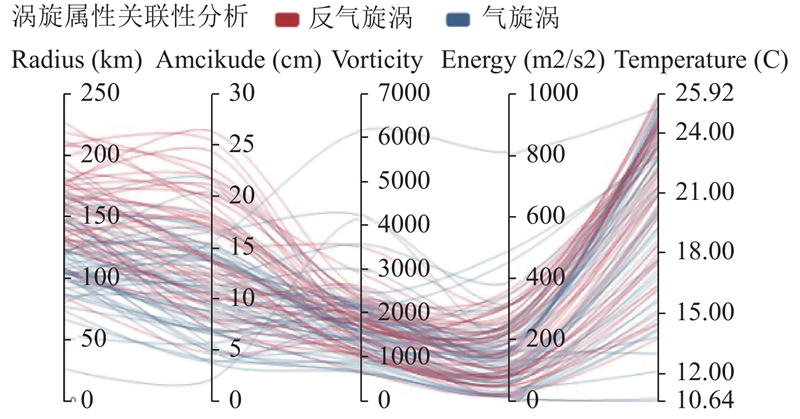
|
图 5 涡旋海洋关联属性平行坐标系 |

|
图 6 涡旋属性空间统计与海洋动能热力图 |
4 实验 4.1 数据
本文使用的卫星高度计资料是法国国家空间研究中心卫星海洋学存档数据中心AVISO 分发的最新版本的多源高度计海面高度异常融合数据, 其空间分辨率为0.25°, 时间分辨率为1 d, 数据格式为NetCDF(Network Common Data Form)网络通用数据格式. 本文选取其区域范围为17°N–42°N, 147°W–172°W, 时间范围为1993年1月1日至2017年12月31日, 长达24年的数据作为研究数据. 根据研究区域尺度可制作为100×100分辨率的样本集, 其中, 1993–2016年的样本集将作为训练集输入YOLOv3网络进行训练, 2017年的样本集将作为测试集检验训练结果的检测效率.
4.2 深度学习神经网络结构本文采用了YOLOv3基本的网络结构, 以Darknet-53[10]网络提取图像特征. 相比YOLOv2中的Darknet-19网络, Darknet-53添加了残差单元, 使用连续的3×3和1×1卷积层, 并将其扩充为53层, 其中包含53个卷积层以及5个最大池化层, 同时, 在每一个卷积层后增加了批量归一化操作和去除随机失活操作, 防止出现过拟合现象.
另外, YOLOv3采用了3个不同尺度的特征图来进行对象检测, 3个尺度分别是32倍降采样, 16倍降采样和8倍降采样. 多尺度融合方式可以使网络同时学习到浅层特征和深层特征, 表达效果更好, 有效解决了YOLO和YOLOv2小目标漏检率高的问题. 本文的涡旋目标尺寸为4×4至6×6不等, 尺寸较小, YOLOv3可以达到更高的召回率.
由于YOLOv3原网络结构中的9个先验框尺寸是基于COCO数据集且网络输入图像分辨率为416×416, 而涡旋检测中待检测目标标注框尺寸如图7所示, 样本图像分辨率为100×100, 因此使用YOLOv3 算法中原有的先验框维度很难得到精确的目标标注框信息. 因此使用YOLOv3算法中原有的先验框维度很难得到精确的目标标注框信息, 需要重新计算先验框以获得更好的检测效率.

|
图 7 样本目标标注框尺寸 |
K-Means聚类的目的是使先验框和临近的真实数据中的标注目标有更大的IOU值, 所以采用K-Means算法时选用标注框与聚类中心标注框之间的IOU值作为距离指标, 使用公式:
| $d(box,centroid) = 1 - IOU(box,centroid)$ | (16) |
进行距离计算.
在K-Means聚类算法中, 将所有标注框中心点的x, y坐标都置为0, 使得所有标注框都处在相同的位置上, 方便计算标注框之间的相似度. 另外, 标注框的宽高为相对于整张图片的比例. YOLOv3网络在检测时会进行3次尺度变换, 以便学习和检测不同尺寸的目标, 而在涡旋检测中, 标注的涡旋目标尺寸均属于小尺寸特征图, 尺寸差别不大. 经过多次测试, 仅使用尺寸小的3个先验框维度便可得到较好的识别结果, 并可加快训练速度. 因此在K-Means聚类时, 设置聚簇个数为3, 最终得到的3组先验框维度中心分别为: (20.48, 17.92), (15.36, 12.8), (10.24, 10.24).
根据本文样本集类别数量以及样本标注框小尺寸的特点, 对网络中3个YOLO层、YOLO层前的卷积层以及部分upsample、route层的参数进行调整, 并使用公式:
| $filters = num*(classes + 5)$ | (17) |
重新计算卷积核个数, 其中
本文在YOLOv3网络结构的基础上对训练参数做出微调. 根据本文样本集图片分辨率, 调整网络输入图像的宽高均为128. 由于显存限制, 将batch设为64, subdivisions设为16, 初始学习率为0.001. 为了得到充分的训练结果, 设置迭代次数为70 200次, 每迭代2000次保存一次训练结果. 本文实验的训练与测试环境采用搭载了2块GTX 1080 Ti显卡的CentOS 7.5.1804系统.
4.4 中尺度涡检测结果本文选取迭代第62 000次的权重结果对2017年研究区域测试集进行涡旋检测. 对初次识别结果进行再识别并且过滤较弱的涡旋后, precision约为0.93, recall约为0.95. Ashkezari等[8]曾构建涡旋特征矩阵, 利用SVM进行分类训练, 表1为本文实验与Ashkezari等人进行的涡旋检测实验的相关内容对比.
由表1可知, Ashkezari等检测结果的precision约为0.92, recall约为0.99. 检测时需要利用滑动窗格扫描研究区域所有数据进行特征计算, 再进行类别判断, 速度较慢. 本文实验结果较之precision值有所上升, recall值有所下降, 但是本文所选研究区域更广, 包含的中尺度涡数量远多于Ashkezari的研究区域, 并且检测速度大大提升, 对研究区域某一天的涡旋检测只需约0.01 s. 之后对涡旋进行准确定位及属性计算时只需对预测框中的SLA数据进行扫描和计算, 大大减少了扫描数据量, 节省了计算时间.
| 表 1 Ashkezari与本文算法性能对比 |
4.5 中尺度涡可视化分析
基于本文提出中尺度涡时空特征及海洋信息协同可视化系统, 对2017年研究区域所识别出的中尺度涡在个数统计、特征分布、尺度统计与分布、属性关联等方面进行分析.
4.5.1 涡旋个数与尺度统计信息图8(a)显示以天位单位观察涡旋个数的变化规律, 气旋涡、反气旋涡均呈现波浪式变化. 图8(b)为涡旋个数月变化, 气旋涡、反气旋涡分别在4月和1月出现次数最多, 在9月和6月出现次数最少. 2017年大多数月份气旋涡数量多于反气旋涡数量, 在第三季度中出现反气旋涡多于气旋涡的情况. 该区域中尺度涡的产生有明显的季节变化, 春季是高发季节, 而秋季产生数量最少. 气旋涡数量的变化基本对应于全部涡旋数量的变化.
图9显示了涡旋尺度统计信息, 不论是气旋涡还是反气旋涡, 涡旋数量极大值都会出现在半径51–155 km范围内, 以及振幅4–20 cm范围内; 但是反气旋涡的半径和振幅的尺度范围更广.
4.5.2 涡旋特征分布信息在等值面特征视图中可看出, 涡旋出现的区域有明显的一系列闭合的海面高度异常等值线, (反)气旋涡对应海面高度(正)负异常, 一般异常绝对值越大, 产生的涡旋半径尺度越大. 涡度较强的区域一般出现在涡核部分, 并且涡度较强处的涡旋半径尺度不会很大, 说明涡旋半径并不是决定涡度强弱的因素. 涡度较强区域均有涡旋的分布, 然而也有部分中等强度涡度区并没有涡旋出现, 同时在涡度极弱的区域不会出现涡旋, 说明涡旋与涡度有很大程度的关联, 但并不是决定因素. 此外, 海洋高动能区域往往出现在涡旋外围, 尤其是多个相邻涡旋之间.

|
图 8 涡旋个数统计图 |
4.5.3 涡旋与海洋属性的关联性分析
为了研究属性间的关系, 通过框选某一尺度范围的属性, 拖动选择框观察其它属性随选中属性的变化趋势. 以2017年6月3日的反气旋涡为例, 如图10(a)至图10(c)所示, 首先框选出0–10 cm的振幅, 可以看到振幅较小的涡旋, 其半径、涡度、涡动能也都处于较低尺度. 随着振幅不断增加, 3种属性尺度也随之上升; 该日气旋涡与反气旋涡的变化规律大体一致, 如图10(d)至图10(f)所示. 由此可知, 涡旋振幅与其它属性存在着一定的正相关关系, 振幅较大的涡旋往往涡度较大, 携带着较大能量, 影响着海洋动能的传播.
涡旋属性空间统计与海洋动能热力图以纬度为单位在空间上对海洋动能和涡旋属性进行统计, 如图11所示. 显而易见, 在25°N–27°N区域, 涡旋半径、振幅、出现频率都出现了最高值, 同时该区域海洋动能也是最强烈的; 其次, 在18°N–25°N和27°N–29°N区域分布着较大尺度半径和振幅的涡旋, 涡旋的出现频率也较多, 同时该区域海洋动能也较高; 在29°N–35°N出现了许多涡旋且半径也较大, 但是由于振幅太小, 并没有对该区域海洋动能产生过多影响. 可以看出涡旋半径、振幅、出现频率均对海洋动能有正影响, 其中振幅的影响更为主要, 与平行坐标系的分析结论一致.

|
图 9 涡旋半径、振幅尺度分布统计图 |

|
图 10 不同振幅范围下的涡旋各属性尺度分布 |

|
图 11 涡旋各属性与海洋动能分布图 |
5 结语
本文将以深度学习为基础的YOLOv3目标检测网络与海洋物理中提取中尺度涡特征的方法相结合, 利用1993–2016年的AVISO卫星高度计融合数据, 针对17°N–42°N, 147°W–172°W的研究区域, 制作深度学习样本集, 调整YOLOv3目标检测模型相关参数并进行训练, 利用训练结果检测该区域2017年的中尺度涡旋, 得到了较好的检测结果, 避免海洋物理中阈值选取对涡旋检测的影响, 大大提高了涡旋检测速度. 之后, 根据涡旋检测结果搭建中尺度涡时空特征及海洋信息协同可视化系统, 对中尺度涡不同维度信息进行交互可视化展示, 并通过各版块联动及交互操作在中尺度涡个数统计、特征分布、尺度分布、属性关联等方面进行分析, 验证了该系统可很好地满足对涡旋和海洋信息进行直观性说明和分析的需求, 大大减少研究人员对繁杂数据的对比分析工作.
| [1] |
Le Traon PY, Morrow R. Chapter 3 ocean currents and eddies. International Geophysics, 2001, 69: 171-215. DOI:10.1016/S0074-6142(01)80148-0 |
| [2] |
Matsuoka D, Araki F, Inoue Y, et al. A new approach to ocean eddy detection, tracking, and event visualization–application to the Northwest Pacific Ocean. Procedia Computer Science, 2016, 80(C): 1601-1611. |
| [3] |
Chelton DB, Schlax MG, Samelson RM, et al. Global observations of large oceanic eddies. Geophysical Research Letters, 2007, 34(15): L15606. |
| [4] |
Okubo A. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep Sea Research and Oceanographic Abstracts, 1970, 17(3): 445-454. DOI:10.1016/0011-7471(70)90059-8 |
| [5] |
Weiss J. The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D: Nonlinear Phenomena, 1991, 48(2–3): 273-294. DOI:10.1016/0167-2789(91)90088-Q |
| [6] |
Beron‐Vera FJ, Olascoaga MJ, Goni GJ. Oceanic mesoscale eddies as revealed by Lagrangian coherent structures. Geophysical Research Letters, 2008, 35(12): L12603. |
| [7] |
Nencioli F, Dong CM, Dickey TD, et al. A vector geometry-based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the southern california bight. Journal of Atmospheric and Oceanic Technology, 2010, 27(3): 564-579. DOI:10.1175/2009JTECHO725.1 |
| [8] |
Ashkezari MD, Hill CN, Follett CN, et al. Oceanic eddy detection and lifetime forecast using machine learning methods. Geophysical Research Letters, 2016, 43(23): 12234-12241. DOI:10.1002/2016GL071269 |
| [9] |
Franz K, Roscher R, Milioto A, et al. Ocean eddy identification and tracking using neural networks. 2018 IEEE International Geoscience and Remote Sensing Symposium. Valencia, Spain. 2018. 6887–6890.
|
| [10] |
Redmon J, Farhadi A. YOLOv3: An incremental im-provement. arXiv:1804.02767, 2018.
|
 2020, Vol. 29
2020, Vol. 29


