引言

ID3算法是著名的决策树, 它是以信息论为基础的一项从上而下的贪心算法, 基于熵的计算从根节点处的所有实例训练集合开始构造决策树. 它通过概率的相关运算来分析对象的属性值, 从而画出像一棵倒立的树形结构图来形象生动地解说实例, 以助于分析决策者做出预测决策. ID3算法规则简单, 容易让人理解, 其算法与最基础的决策树算法^[1]保持一致, 一般用来解决离散值一类的问题, 构造的树尤为形象地说明结果, 一目了然, 得到了众多学者的喜爱.

目前, ID3算法是众多决策树构造算法中应用得最为广泛的一种, 如在医学、教学、公司业绩上的应用等. 孙道^[2]把工厂所关注的特征变量对象返回的期望值传递给ID3算法中递归过程, 构造出决策树模型, 提高算法在其他应用中的移植性. 以上的学者是把决策树ID3算法运用到实际实例中去, 但并没有进行改进及优化算法, ID3算法自身所带的局限性还是存在的, 还是有不少问题值得研究的. ID3算法进行局部分析, 每次只选择一个属性分析, 从而产生大量规则以致效率会下降, 并且只能做到局部最优; 它优先考虑属性值数目最多的属性, 但问题是属性值多不一定是最优的测试属性; 它构造的决策树是单变量决策树, 而忽略了属性之间可能存在的相互依赖的关系; 它的计算方法比较复杂, 由于是关于对数log的运算, 所以运算量非常大; 它对信息系统的数据没有进行简化, 存在冗余的信息, 当系统大量信息时会变得复杂, 构造决策树所需的时间也会增多.

由于ID3算法只能处理离散属性值, Quinlan又投入决策树算法的研究当中去, 于1993年提出了以ID3为基础核心的C4.5算法, 它不仅能处理离散属性值, 还能处理连续属性值, 并且继承了ID3算法的所有优点. 接着, Breman等人提出了构造一颗二叉树的分类与回归树算——CART算法, 它具有非常强大的统计解析能力, 处理数据后得到一颗二叉树, 简洁且易懂. 此外, IBM的研究人员提出了SLIQ算法, 具有很好的伸缩性. 后来, 很多学者致力于研究多决策树综合技术, 探索出各种多决策树的分类方法, 例如Schapire R提出的Boosting、Breiman提出的Bagging、Random Forest分类方法等. 再后来, 决策树的增量算法出现了, 有增量ID3、ID5R等^[3].

黄爱辉等人利用数学上等价无穷小的性质提出一种新的改进的ID3算法^[4]. 杨霖等人提出了基于粗糙集、粒计算和分类矩阵的ID3改进算法^[5]. 作者引入修正参数来改进ID3算法倾向于多值属性选取的问题^[6,7]. 也有学者利用模糊规则提出了两种ID3改进算法^[8,9]. 李建等人^[10]在ID3的基础上引入属性重要度值用以计算新的信息熵, 并在信息增益计算中加入关联度函数比,提出了AFIV-ID3算法, 克服了ID3多值偏向的缺点. 大部分学者都是针对ID3取值较多的属性和只能处理离散型数据这两个缺陷进行改进及其优化算法的, 少有学者利用粗糙集中的属性约简去删除系统中多余的信息.

于天佑等人^[11]研究表明在选定的特定类的数量相对全部决策类的数量较少时,约简的结果可能会更短, 约简的效率也会有不同程度的提升. 邬阳阳等人^[12]当前研究中拓展粗糙集模型在约简理论完善、大数据处理、特殊数据处理等3个方面的问题依然存在. 尹继亮^[13]利用区间值、正域, 并引入局部约简的概念, 设计了基于差别矩阵的局部约简算法. 粗糙集属性约简算法是一种数据预处理的有效方法,但指标多的时候, 使用区间值与正域求解是非常困难, 运行起来效率低下, 因此属性约简的应用研究相对较少. 少有学者应用分辨函数去求解属性约简, 更少学者想到要把ID3中计算熵公式中的复杂对数进行化简. 本文将介绍ID3的基本原理, 针对ID3信息系统存在冗余知识与计算方法复杂这两点缺点进行改进, 提出了基于粗糙集属性约简的简化ID3算法, 重点在于改进算法的实例分析、实验仿真和结果分析比较.

1 ID3算法的基本理论

决策树算法这个说法最早出现于上世纪60年代, 到了1979年, 澳大利亚学者Quinlan提出了迭代两分器算法(Iterative Dichotomizer3), 故简称ID3算法. 决策树是数据挖掘分类算法中的一个重要分支, 是一种归纳学习的贪心算法, 属于有监督学习法. 它主要是以实例为基础, 通过概率的相关运算来分析对象的属性值, 从而画出像一棵倒立的树形结构图来形象生动地解说实例, 以助于分析决策者做出预测决策. 下面简述一下ID3的基本理论.

对于一组实例训练样本集合U, 共有n个样本集合; 分类属性集合为C, 有c个不同的类; 决策属性集合为D, 将实例训练集合分为d个不同的类 ${D_i}(i = 1,$ $2,\cdots,d)$ , 每个类的个数为 ${{{n}}_i}(i = 1,2,\cdots,n)$ , 则 ${D_i}$ 类在集合U中出现的概率为 ${P_{{i}}} = {{{{{n}}_i}} / n}$ , 则计算集合U划分d个类的信息熵为 ${C_i}\left( {i = 1,2,\cdots,c} \right)$ .

$H(U) = - \sum\nolimits_{i = 1}^d {{P_{\rm{i}}}{{\log }_2}{P_i}} $

(1)

假设分类属性集合C的属性值集合为Values(C)， ${C_{{C_i}}}$ 是集合U中属性C的值为 ${C_i}$ 的样本子集, 该子集实例个数为t, 属于 ${D_i}$ 类的个数有 ${{{t}}_i}(i = 1,2,\cdots,t)$ , 子集 ${C_i}$ 在属性集合C 出现的概率为 ${P_{{t_i}}} = {{{t_i}} / t}$ , 则属性集合C划分为c个类的信息熵为:

$H({C_{{C_{\rm{i}}}}}) = - \sum\nolimits_{i = 1}^{\rm{t}} {{P_{{t_i}}}{{\log }_2}{P_{{t_i}}}} $

(2)

定义1. 选择分类属性C后的实例训练样本集合U的信息熵为:

$H\left( {U,C} \right) = \sum\nolimits_{i = 1}^t {{{\left| {{C_{{C_i}}}} \right|} / {\left| U \right|}}H\left( {{C_{{C_i}}}} \right)} $

(3)

即在选择分类属性集合C后的信息熵为其每一个子集 ${C_{\rm{i}}}$ 的信息熵的加权和, 权值为子集 ${C_{{C_{\rm{i}}}}}$ 中值的个数占集合U的个数的比例.

定义2. 属性C相对实例训练样本集合U的信息增益为:

$G{{ain}}(U,C) = H(U) - H(U,C)$

(4)

信息增益指的是因知道属性C后而导致集合U的信息熵下降, Gain(U,C)越小, 说明H(U)下降得越快, H(U,C)所含的信息量就越大, 属性C 就难以从众多的分类属性中分类出来. 所以, ID3算法才选择信息增益最高的属性作为测试属性.

2 基于粗糙集属性约简的简化ID3算法 2.1 属性约简

定义3. 设 $D \subseteq C$ , 如果D是独立的, 且IND(D) =IND(C), 那称D是等价关系族C的一个约简(Reduct).

一个信息系统里面含有很多知识信息, 有些知识很可能是重复的或是没有必要, 也就是说这些知识对该信息系统是冗余的, 把多余的知识删掉后剩下的知识就是知识约简. 即知识约简还是与原来的信息系统保持有同样的分类能力的, 只不过是把一些没必要的知识删去而已, 从而使得分类时更加简便、精确.

定理1^[14]. 设 $X \subseteq C$ ,

1)如果 $\forall {{x}} \in RED(X)$ , 那:

$SI{G_{(RED(X) - \left\{ {\rm{x}} \right\})}}(x) > 0$

(5)

2)如果 $\forall {{x}} \in X - RED( X )$ , 则:

$SI{G_{RED\left( X \right)}}\left( x \right) = 0$

(6)

从上面的命题可以看出, 知识约简中每一个元对约简中的其余元都是必不可少, 而约简外的其他元对于约简中的任何一元都是不必要, 即是可以删去.

定义4. 设C和D为论域U上的等价关系, D的C正域记作 $PO{S_C}\left( D \right)$ , 定义为:

$PO{S_C}D = \mathop \cup \limits_{} \underline C X$

(7)

其中, $X \in U/D$ .

显然, 相对约简是两个属性之间的关系. POS_C(D)解释了知识 ${U / C}$ 的信息正确归类到属性D的等价类中的准确性.

定义5. 设C和D为论域U上的等价关系族, $R \in $ P, 如果:

$PO{S_{IND\left( C \right)}}\left( {IND\left( D \right)} \right) = PO{S_{IND\left( {C - \left\{ R \right\}} \right)}}\left( {IND\left( D \right)} \right)$

(8)

就称R为C中D可省的, 反之就称R为C中D不可省^[3]的. 如果C中任意一个关系R都是不可省的, 就称是D独立的, 也就是说C是相对于D独立的.

定义6. 设 $S \subseteq C$ , 称S为C的约简, 当且仅当S是C的D独立子族, 且:

$PO{S_S}\left( D \right) = PO{S_C}\left( D \right)$

(9)

即称之为相对约简.

定理2. C的D核等于C的所有D约简的交:

$COR{E_D}\left( C \right) = \cap RE{D_D}\left( C \right)$

(10)

定义7. 令T=(U,A,V,f)为一个信息系统, U中元素的个数记为 $| U | = {{n}},| A | = m$ , T的分辨矩阵M定义为一个n阶对称矩阵^[3], 其i行j列处的元素可定义为:

$ {{{m}}_{ij}} = \left\{ {a \in A|f\left( {{x_i},a} \right) \ne f\left( {{x_j},a} \right)} \right\},{\text{其中}}{{i}}, {{j}}=1,\cdots,{{n}}. $

(11)

其中, f称为分辨函数, 使得 ${{{m}}_{ij}}$ 可以区分属性.

对于每一个 ${{a}} \in A$ , 指定布尔变量 $\overline {{a}} $ ^[2], 将T的f函数定义为一个m元布尔函数:

$\rho \left( {\overline {{{{a}}_1}} ,\overline {{a_2}} ,\cdots,\overline {{a_m}} } \right) = \wedge \left( { \vee {m_{ij}}|1 \le j < i \le n,{m_{ij}} \ne \emptyset } \right)$

(12)

其中, $ \wedge $ 为合取, $ \vee $ 为析取. 可以看出, 分辨函数f的析取范式中的每一个合取式对应一个约简, 约简的交集即为核.

2.2 化简算法

下面简化的公式是基于本章中的式(1), 假设论域U中的训练样本集只有两类, 即决策属性集合D中只有两种类别, 称为正例与反例, 设其占的个数分别为P与N, 分类属性集合C中对应的正例与反例的个数分别为 ${p_i},{n_i}$ , 则公式可以写成:

$ \begin{array}{*{20}{l}} {H\left( {U,C} \right) =\! \displaystyle\sum\nolimits_{i = 1}^t {\left( {{n_i} + {p_i}} \right)/\left( {N + P} \right) \cdot \left[ { - {p_i}/\left( {{n_i} + {p_i}} \right){{\log }_2}{p_i}/} \right.} }\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {{n_i} + {p_i}} \right) - {n_i}/\left( {{n_i} + {p_i}} \right){{\log }_2}{n_i}/\left( {{n_i} + {p_i}} \right)} \right] \\ =\! \displaystyle\sum\nolimits_{i = 1}^t {1/\left( {N \!+\! P} \right)} \left[ { - {p_i}{{\log }_2}{p_i}\!/\!\left( {{n_i} \!+\! {p_i}} \right) \!-\! {n_i}{{\log }_2}{n_i}/\left( {{n_i} \!+\! {p_i}} \right)} \right] \\ =\! - 1/\left( {N \!+\! P} \right) {\displaystyle\sum\nolimits_{i = 1}^t {\left[ {{p_i}{{\log }_2}{p_i}\!/\!\left( {{n_i} + {p_i}} \right) \!+\! {n_i}{{\log }_2}{n_i}\!/\!\left( {{n_i} \!+\! {p_i}} \right)} \right]} } \end{array} $

由对数换底公式: ${\log _a}b = {{{{\log }_c}b} / {{{\log }_c}a}}$ , 其中a,b,c为大于0且不等于1的常数.

故:

$ \begin{array}{*{20}{l}} {H\left( {U,C} \right) = - 1/\left( {N + P} \right) \cdot \displaystyle\sum\nolimits_{i = 1}^t }\\ {\left[ {{p_i}\left( {\ln \left( {{p_i}/{n_i} + {p_i}} \right)} \right)/\ln 2 + {n_i}\left( {\ln \left( {{n_i}/{n_i} + {p_i}} \right)} \right)/\ln 2} \right] } \\ =\!- 1/\left( {N + P} \right)\ln 2\displaystyle\sum\nolimits_{i = 1}^t {\left[ {{p_i}\ln \left( {{p_i}/{n_i} \!+\! {p_i}} \right) \!+\! {n_i}\ln \left( {{n_i}/{n_i} \!+\! {p_i}} \right)} \right]} \end{array}$

又由数学分析中的泰勒公式^[15], 有:

$\ln \left( {1 + x} \right) = x - {{{x^2}} / 2} + {{{x^3}} / 3} + \cdots + {\left( { - 1} \right)^{n - 1}}{{{x^n}} / n} + {\rm{o}}\left( {{x^n}} \right)$

得 $\ln ( {1 - x} ) = - x - {{{x^2}} / 2} - {{{x^3}} / 3} + \cdots + ( { - 1} ){{{x^n}} / n}$ .

当x趋于0时, $\ln \left( {1 - x} \right) \approx - x - {{{x^2}} / 2}$ .

所以:

$ \begin{array}{l} \begin{array}{*{20}{l}} {H\left( {U,C} \right) = - 1/\left( {N + P} \right)\ln 2}\\ { \cdot \displaystyle\sum\nolimits_{i = 1}^t {\left[ {{p_i}\ln \left( {1 - {n_i}/{n_i} + {p_i}} \right) + {n_i}\ln \left( {1 - {p_i}/{n_i} + {p_i}} \right)} \right]} } \end{array}\\ \begin{array}{*{20}{l}} { \approx - 1/\left( {N + P} \right)\ln 2}\\ { \cdot \displaystyle\sum\nolimits_{i = 1}^t {\left[ \begin{array}{l} {p_i}\left( { - {n_i}/{n_i} + {p_i} - {n_i}^2/2{{\left( {{n_i} + {p_i}} \right)}^2}} \right) + \\ {n_i}\left( { - {p_i}/{n_i} + {p_i} - {p_i}^2/2{{\left( {{n_i} + {p_i}} \right)}^2}} \right) \end{array} \right]} } \end{array}\\ \begin{array}{*{20}{l}} { \approx\! - 1/\left( {N + P} \right)\ln 2 \cdot \displaystyle\sum\nolimits_{i = 1}^{\rm{t}} {} }\\ {\left[ { - 2{n_i}{p_i}/{n_i} + {p_i} - {n_i}{p_i}\left( {{n_i}/{{\left( {{n_i} + {p_i}} \right)}^2} + {p_i}/{{\left( {{n_i} + {p_i}} \right)}^2}} \right)/2} \right]} \end{array} \\ \approx- 1/\left( {N \!+\! P} \right)\ln 2\!\displaystyle\sum\nolimits_{i = 1}^t {\left[ { - 4{n_i}{p_i}\!/\!2\left( {{n_i} + {p_i}} \right) \!-\! {n_i}{p_i}/2\left( {{n_i} \!+\! {p_i}} \right)} \right]} \end{array} $

$\begin{array}{l} \approx - {1 / {\left( {N + P} \right)\ln 2}}\displaystyle\sum\nolimits_{i = 1}^t { - {{5{n_i}{p_i}} / {2\left( {{n_i} + {p_i}} \right)}}} \\ \approx {5 / {\left( {N + P} \right)\ln 2}}\displaystyle\sum\nolimits_{i = 1}^t {{{{n_i}{p_i}} / {{n_i} + {p_i}}}} \end{array}$

因为 ${5 / {\left( {N + P} \right)\ln 2}}$ 为常数, 故信息熵简化公式可写为: ${{g = }}\displaystyle\sum\nolimits_{i = 1}^t {{{{n_i}{p_i}} / {{n_i} + {p_i}}}} $ .

3 实例分析

本文中的例子摘自李雄飞等著者编写的第二版《数据挖掘与知识发现》, 详情见参考文献[3]. 下面以表1为例, 运用ID3算法构造决策树. 该表中一共有14个样本, 样本构成的集合为U, 分类属性一共有4种, 决策属性只有1种, 且PlayTennis有两个不同的值{yes, no}, 也就是有两个不同类 ${D_1},{D_2}$ .

为了便于计算, 把表1转化为 PlayTennis训练集数值化数据, 如表2.

第1步. 由决策表2 PlayTennis训练集数值化数据, 可得:

$U = \left\{ {{x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8},{x_9},{x_{10}},{x_{11}},{x_{12}},{x_{13}},{x_{14}}} \right\}$

$\begin{array}{l} {U / C} = \left\{ \begin{array}{l} \{ {x_1}\} ,\{ {x_2}\} ,\{ {x_3}\} ,\{ {x_4}\} ,\{ {x_5}\} ,\{ {x_6}\} ,\{ {x_7}\} , \\ \{ {x_8}\} ,\{ {x_9}\} ,\{ {x_{10}}\} ,\{ {x_{11}}\} ,\{ {x_{12}}\} ,\{ {x_{13}}\} ,\{ {x_{14}}\} \\ \end{array} \right\}{U / D} =\\ \{ \{ {x_1},{x_2},{x_6},{x_8},{x_{14}}\} ,\{ {x_3},{x_4},{x_5},{x_7},{x_9},{x_{10}},{x_{11}},{x_{12}},{x_{13}}\} \} \end{array} $

$k = {{|PO{S_C}D|} / {|U|}} = 1$

故该决策表是一致决策表, 即集合D依赖于集合C.

第2步. 画出决策表的分辨矩, 见表3

第3步. 通过分辨函数求出属性的约简.

由画出决策表的分辨矩, 见表3, 得分辨函数为:

$ \begin{array}{l} {{f}} = O\left( {O \vee W} \right)\left( {O \vee T} \right)\left( {O \vee T \vee W} \right)\left( {O \vee T \vee H} \right) \\ \left( {O \vee T \vee H \vee W} \right) \left( {T \vee H \vee W} \right)W\left( {T \vee H} \right) \wedge \left( {T \vee W} \right) \\ \left( {O \vee H} \right)\left( {H \vee W} \right)\left( {O \vee H \vee W} \right)= O\left( {T \vee H \vee W} \right)W\left( {T \vee H} \right)\\ = OW \wedge \left( {T \vee H} \right) = OWT \vee OWH \end{array} $

因此, 决策表的核为: $OWT \cap OWH = OW$

即说明Outlook与Wind这个属性在做决策分类时是必不可少, 该系统的分类属性只需要Outlook、Wind、Temperature 或者Outlook、Wind、Humidity这3个就可以进行归类.

第4步. 选择Outlook、Wind、Temperature这3个属性进行决策, 用信息熵简化公式g计算.

Outlook: ${g_o} = {{2*3} / {(2 + 3) + {{4*0} / {\left( {4 + 0} \right) + {{3*2} /}{\left( {3 +} \right. } }}}} $ ${\left. { 2} \right)}=6/5 $ 同理, 可求得: ${g_w} = 27/8$ , ${g_T} = 37/12$ .

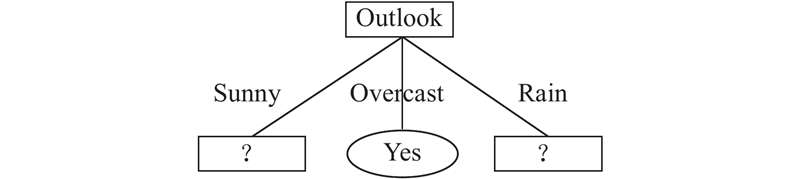
显然, Outlook的信息熵最小, 故取其作为根节点, 画出部分树如图1.

第5步. 在属性Outlook的条件下继续计算分类属性的信息熵, 选择最小者作为节点.

同理, 当Outlook取值为Sunny时, 有:

Wind: ${g_{{\rm {Sunny}}{_W}}} = 7/6$ .

Temperature: ${g_{{\rm {Sunny}}{_T}}} = 1/2$ .

故在树的左边第二节点选择属性Temperature.

以此类推, 直到当前节点的训练样本实例是属于同一类时就可以结束计算了, 得出一棵决策树如图2.

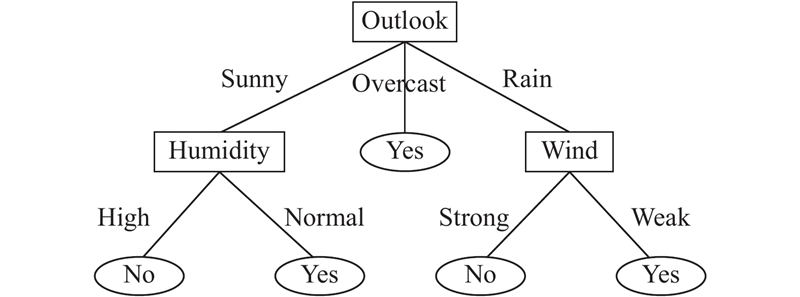
如果在第三步中选择Outlook、Wind、Humidity这3个属性的话, 得到决策树结果跟用传统ID3算法构造的一样, 如图3.

4 仿真实验与结果分析 4.1 仿真实验环境与实验内容

本实验涉及的设备、语言等具体环境如表4.

为了验证改进算法的运行时间比ID3的少, 本文用C++语言编写程序进行实验, 实验数据主要来源于UCI Machine Learning Repository, 选取了Balance Scale Data Set 库, 网址是: http://archive.ics.uci.edu/ml/datasets.html.

决策属性为Class Name: Yes, No, 分类属性有4种, 如表5.

这个数据集是为了模拟心理学实验结果而产生. 本文中选取的每个例子被分类为平衡秤尖端在右侧或是在向左端, 实验中分别标记为Yes, No. 属性是左重量, 左距离, 右重量和右距离.

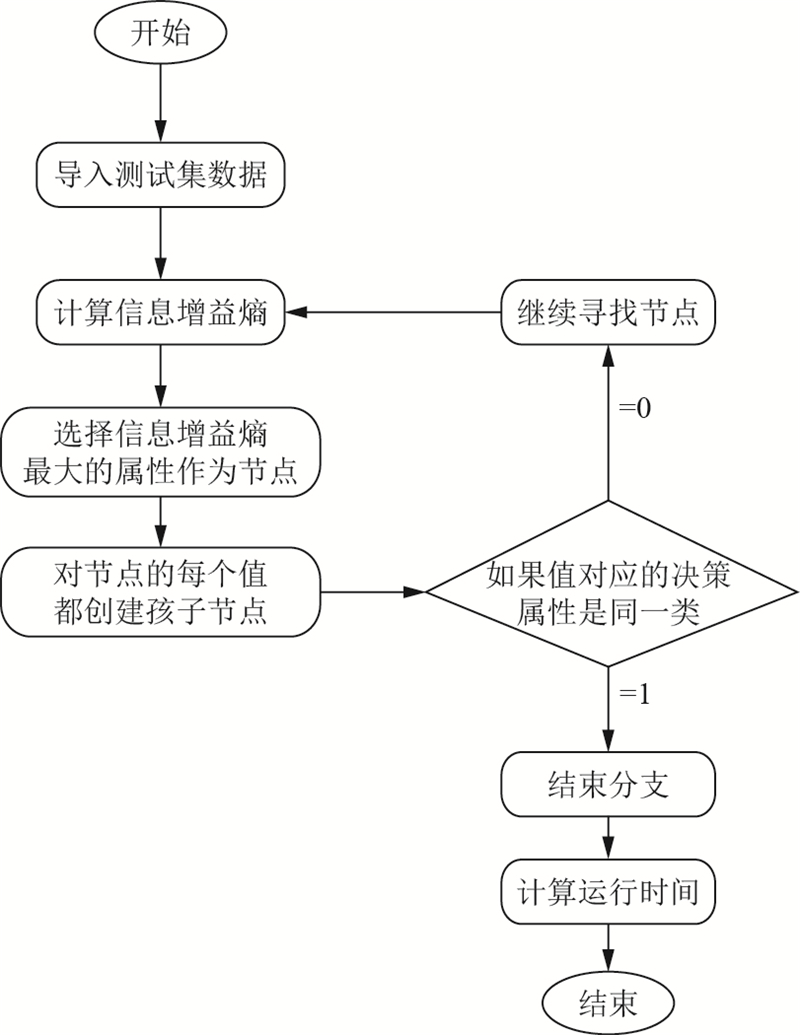
该实验用C++编程的流程如图4.

4.2 实验结果分析 4.2.1 算法的正确性与可行性

ID3算法用的信息熵公式:

$H\left( U \right) = - {p_1}{\log _2}{p_1} - {p_2}{\log _2}{p_2}$

(14)

其中, ${p_1},{p_2}$ 分别指的是实例训练集合中正例与反例所占的比例.

基于粗糙集方法的属性约简化简算法用的信息熵公式为:

$H\left( {{U'}} \right) = {{{p_i}*{n_i}} / {\left( {{p_i} + {n_i}} \right)}}$

(15)

其中, ${p_i},{n_i}$ 分别指的是实例训练集合中正例与反例的个数.

由此可画出式(14)与式(15)的函数图像如图5.

由图5可知, ID3算法与基于粗糙集属性约简的简化ID3算法的熵的范围都是 0到1, 但是改进的算法的熵的变化幅度比ID3的大. 基于粗糙集属性约简的简化ID3算法运算复杂度要比ID3算法的要低得多, 省去了log对数的计算, 并且保持了跟传统ID3算法一样的准确率. 因此, 改进的算法并没有改变熵函数的性质, 可见其的正确性与可行性, 并且扩大了熵的变化幅度.

4.2.2 算法的优势

通过实验可知, 基于粗糙集方法的属性约简化简算法的计算时间比ID3少, 具体如表6.

从上述仿真实验以及分析可以得出以下结论:

1) 基于粗糙集方法的属性约简化简算法的熵函数性质并没有改变, 继承了ID3的所有优点;

2) 基于粗糙集方法的属性约简化简算法的计算时间比ID3的少, 这无疑是一个优势.

5 结论

本文先通过文献综述总结了决策树ID3的历史发展过程, 概述了当前学者研究改进及优化决策树ID3算法的现状和结论. 本文通过实例分析与实验验证, 基于粗糙集属性约简的简化ID3算法的优势之一是删掉了冗余的知识, 是决策系统更加精炼简洁, 能快速找出关键的分类属性; 优势之二是保持了ID3的一切优点, 与ID3有同样的准确率与精度; 优势之三是选取测试属性的计算公式中没有复杂的对数函数, 只有简单的加法、乘法和除法, 经实验证明, 运算时间比ID3的要少. 缺点是在求属性约简时, 规模过大的话, 用分辨函数求解的难度就会变大.

总的来看, 本文处于研究阶段并没有把结论应用到社会生活实例中去, 所以本文还是存在不足之处, 还是有很多值得再去深入研究、探索的地方, 未来的研究方向以下这两点: 1)本文提出的基于粗糙集的决策树ID3算法相对ID3来说确实是有优势, 但在求属性的约简过于繁琐, 所以下一步的研究是寻求更加简单的方式去求属性的约简, 完善基于粗糙集方法的属性约简化简决策树算法. 2)由于时间及其能力不足等等客观条件的限制, 本文没有将改进的算法运用到更多的实际生活例子中去并用于预测, 因此该论文得到发展的话, 应该更重视研究把此算法改得更加合理性、科学性、可行性.