对于一个时间序列趋势分析问题, 一般不只限于一种时序预测模型可以使用, 特别在数据量较大的情况下, 数据量的增多意味着信息的增多, 只根据误差大小选择单一模型进行预测可能会导致部分有用信息的流失. 因此对于数据量较大的时间序列趋势分析, 进行组合预测很有必要. 组合预测模型是将多个候选预测模型的预测结果赋予合适的权值进行组合, 核心问题包括两个方面: 预测模型选择、权重确定方式.

可供选择的单项预测模型包括灰色预测模型^[1]、时间序列模型^[2]以及机器学习模型, 前两者是传统的统计学模型, 机器/深度学习模型应用于组合预测模型则是比较新的探索^[3–6].

组合预测模型的权重选择方式包括层次分析法^[6]、熵权法^{[7, 8]}和最优加权法^[9], 以上方法原理是基于预测数据本身的性质; 还有一类方法是基于单项模型预测误差来确定权重的, 如最小二乘法^{[10, 11]}, 改进后的广义加权最小二乘法^{[12, 13]}, 局部加权最小二乘法^{[14, 15]}.

正则化和交叉验证是机器学习建立模型时使用的一种用于优化模型参数的方法, Hansen和Racine^[16]提出了基于交叉验证的Jackknife模型平均(JMA)方法, 并证明了JMA方法可使模型权重选择得到优化; Zhao等^[17]在JMA方法的基础上开发了一个基于K折交叉验证的权重选择准则, 并证明了使用该准则可以产生更准确的预测. Sebastian Bayer^[18]则在组合权重的选择中使用正则化降低单项预测间的多重共线性, 并证实这种方法可以通过稳定模型来提高模型预测能力.

通过阅读以上文献, 发现以往针对正则化和交叉验证的研究有两个特点: 一方面, 正则化和交叉验证对组合模型的影响都独立研究, 不能够发现这两者共同作用于组合模型的影响规律; 另一方面, 以上研究着重于比较正则化或交叉验证与其他权重选择方法的影响能力, 不注重讨论它们本身应用时的优化规律. 有鉴于此, 本文将以最小二乘加权组合预测模型为基础, 这种组合预测模型属于常规组合模型设计, 但其结构灵活, 使用广泛, 具有一定的改良和研究价值; 使用正则化和交叉验证对其进行优化, 正则化项选择L₁范数和L₂范数, 交叉验证选择K折交叉验证和留一交叉验证, 实验数据选择我国铁路客运量2005~2018年的月度数据, 由于该数据具有明显时间序列周期性, 组合预测的单项模型选择为适合分析周期性时间序列的SARIMA模型和Holt-Winters模型.

1 组合预测模型理论分析 1.1 单项模型理论

(1) SARIMA建模原理和步骤

SARIMA模型称为季节性差分自回归移动平均模型, 能够通过在ARIMA模型的基础上通过适当次数的季节性差分来消除序列的不稳定性, 适合处理具有趋势性和周期性的时间序列^[19]. 也写作SARIMA(p, d, q)(P, D, Q)[m]模型, 由6个部分组成: AR(自回归)、I(整合/差分)、MA(移动平均)、SAR(季节性自回归)、SI(季节性整合/差分)、SMA(季节性移动平均), 每个模型均是SARIMA的特殊情况, 各自对应的参数为p, d, q, P, D, Q, 还有一个参数[m]表示季节性周期长度, 本文的实验数据m值为12; 模型结构为:

$\varPhi (B){\varPhi _m}(B){\nabla ^d}\nabla _m^D{Y_t} = \Theta (B){\varTheta _m}(B){\varepsilon _t}\;\;\;$

(1)

$\left\{ {\begin{array}{l} {\varTheta (B) = 1 - {\theta _1}B - \cdots - {\theta _q}{B^q}} \\ {\varPhi (B) = 1 - {\varphi _1}B - \cdots - {\varphi _p}{B^p}} \\ {{\varTheta _m}(B) = 1 - {\theta _1}{B^m} - \cdots - {\theta _Q}{B^{Qm}}} \\ {{\varPhi _m}(B) = 1 - {\varphi _1}{B^m} - \cdots - {\varphi _P}{B^{Pm}}} \end{array}} \right.\;$

(2)

其中, B是滞后算子, d是趋势差分次数, D是以周期m为步长的季节差分次数, $\left\{ {{\varepsilon _t}} \right\}$ 为白噪声序列.

使用SARIMA模型建模的过程为:

1)检验原序列平稳性, 对不平稳的原序列通过d次差分使其满足平稳性条件;

2)对平稳化后的时间序列数据绘制自相关图和偏自相关图, 以此初步识别模型的p、q、P、Q可以取值的范围, 然后使用AIC准则作为寻找最佳模型的准则, 在所有通过检验的模型选择AIC值最小的模型作为最适合的SARIMA模型;

3)对已经选定的模型进行检验, 观察模型参数是否通过检验以及残差序列是否为白噪声序列, 如果模型参数未能通过检验或残差序列存在相关性, 则模型需要重新拟合;

4)使用通过检验的SARIMA模型进行时间序列预测.

(2) Holt-Winters模型

Holt-Winters模型是一种可用于周期性和趋势性时间序列预测问题的模型, 也称作三次指数平滑法. 模型思想可认为是对一组时序数据长期趋势、周期变化和随机扰动的分解, 因为Holt-Winters模型是在保留了随机扰动信息的一次指数平滑模型和保留了趋势信息的二次指数平滑模型的基础上添加一个新参数, 使其对时间序列的周期性进行描述, 模型分为累加模型和累乘模型两种.

累加模型的数学表达如下:

$\left\{ {\begin{array}{*{20}{l}} {{s_t} = \alpha ({X_t} - {p_{t - k}}) + (1 - \alpha )({s_{t - 1}} + {t_{t - 1}})} \\ {{i_t} = \beta ({s_t} - {s_{t - 1}}) + (1 - \beta ){i_{t - 1}}} \\ {{p_t} = \gamma ({x_t} - {s_t}) + (1 - \gamma ){p_{t - k}}} \\ {{X_{t + h}} = {s_t} + h \cdot {i_t} + {p_{t - k + h}}} \end{array}} \right.\;$

(3)

累乘模型的数学表达为:

$\left\{ {\begin{array}{*{20}{l}} {{s_t} = \alpha (\dfrac{{{X_t}}}{{{p_{t - k}}}}) + (1 - \alpha )({s_{t - 1}} + {t_{t - 1}})} \\ {{i_t} = \beta ({s_t} - {s_{t - 1}}) + (1 - \beta ){i_{t - 1}}} \\ {{p_t} = \gamma (\dfrac{{{x_t}}}{{{s_t}}}) + (1 - \gamma ){p_{t - k}}} \\ {{X_{t + h}} = ({s_t} + h \cdot {i_t}){p_{t - k + h}}} \end{array}} \right.\;$

(4)

在上述公式中, X_t为t时刻的观测值, s_t、i_t、p_t分别为t时刻的稳定成分、周期成分和趋势成分, h为区间外预测期数, k为周期长度, α、β、γ为平滑参数且α、β、γ∈[0,1].

累加模型适合于周期趋势不随时间变化而发生变化的时间序列, 累乘模型适合于周期趋势随时间变化发生变化的时间序列, 在使用Holt-Winters模型进行单项模型预测时需要根据实验数据自身特点选择其中一个模型.

1.2 组合模型理论

对于一个n期时间序列预测问题, 观测数据为 $x= \left\{ {{x _1},} \right. $ $\left. {{x_2}, \cdots ,x_t, \cdots,{x _n}} \right\}$ , 其中x_t表示变量在t时刻的观测值, 选取J个单项预测模型对其进行预测, 得到J个预测模型 $\left\{ {{\varphi _1},{\varphi _2}, \cdots, {\varphi _J}} \right\}$ , 则在t时刻对序列的预测值为 $\left\{ {{\varphi _1}(t),{\varphi _2}(t), \cdots ,{\varphi _J}(t)} \right\}$ , 组合预测的思想就是对每个模型的预测值通过适当的加权方法进行组合, 设单项预测模型的权重为 $\left\{ {{\omega _1},{\omega _2}, \cdots, {\omega _J}} \right\}$ , 且 $\displaystyle\sum\nolimits_{i = 1}^J {{\omega _i} = 1} $ , 则组合模型的数学表达式为:

$\;{\varPhi _t} = {\omega _1}{\varphi _1}(t) + {\omega _2}{\varphi _2}(t) + \cdots + {\omega _J}{\varphi _J}(t) = \sum\limits_{i = 1}^J {{\omega _i}{\varphi _i}(t)} \;$

(5)

权重选择的常见思想是根据每个模型的预测精度, 即预测值与观测值之间的误差来进行权重选择, 可供使用的误差包括相对误差、绝对误差、对数误差和误差平方和等, 本文将在使用误差平方和作为加权依据的最小二乘加权法的基础上, 加入正则化项并使用交叉验证对加权法则进行优化, 进而研究正则化和交叉验证对组合预测模型的优化能力.

(1) 最小二乘加权法

在组合模型中经常使用预测值与观测值之间的误差平方和最小化来计算权重系数, 这种方法被称为最小二乘法^[20], 对于一个线性组合预测模型:

在t时刻组合预测模型的预测值为 ${\varPhi _t}$ , 第i种单项预测模型的预测值为 ${\varphi _i}(t)$ , 观测值为 ${x_t}$ ; 那么在t时刻, 第i种单项预测模型的预测误差为 ${e_i}(t) = {\varphi _i}(t) - {x_t}$ , 则组合预测模型在t时刻的预测误差为 ${e_t} = ({\varPhi _t} - {x_t}) = $ $ \displaystyle\sum\nolimits_{i = 1}^J {{\omega _i}\left[ {{\varphi _i}(t) - {x_t}} \right]} = \displaystyle\sum\nolimits_{i = 1}^J {{\omega _i}{e_i}(t)} $ , 为了使组合模型的预测值最优, 将预测值最优问题转化为组合模型性误差最小化问题, 组合预测模型的误差平方和为 $Q = \displaystyle\sum\nolimits_{t = 1}^n {e_t^2} = {\displaystyle\sum\nolimits_{t = 1}^n {\left( {\displaystyle\sum\nolimits_{i = 1}^J {{\omega _i}{e_i}(t)} } \right)} ^2}$ , 在实际运算时一般采用平均误差平方和MSE作为组合预测模型的误差衡量准则, 则基于上述理论, 最小二乘加权法的数学表达为:

$ \left\{ {\begin{array}{*{20}{l}} {\min Q = \dfrac{1}{n}{{\displaystyle\sum\nolimits_{t = 1}^n {\left( {\displaystyle\sum\nolimits_{i = 1}^J {{\omega _i}{e_i}(t)} } \right)} }^2}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm s.t.} \displaystyle\sum\nolimits_{i = 1}^J {{\omega _i}} = 1} \\ {\varPhi _t} = {\omega _1}{\varphi _1}(t) + {\omega _2}{\varphi _2}(t) + \cdots + {\omega _J}{\varphi _J}(t) = \displaystyle\sum\nolimits_{i = 1}^J {{\omega _i}{\varphi _i}(t)} \end{array}} \right. $

(6)

(2) 正则化

正则化技术广泛应用于机器学习和深度学习算法中, 常用于防止模型过拟合或提高模型泛化能力, 其思想是在经验风险(本文指误差平方和最小化函数)中加上一个正则化项来控制权重系数矩阵的值使权重矩阵缩减或变得相对稀疏, 从而避免有些特征在模型中影响力过高导致的模型过拟合^[21].

在组合预测模型中, 如果几个单项预测模型的预测效果表现的比较接近, 直接选取其中预测精度最高的模型进行组合可能会失去一些有用的信息, 但如果将所有单项预测模型一起进行组合, 在传统的加权方式下, 组合模型权重选择会很大程度上偏向在训练数据中预测误差最小的单项预测模型, 形成的组合模型会在训练数据上表现的比较好, 但是在预测数据上则可能会出现“过拟合”现象, 从而降低组合模型对新数据的预测能力. 基于这种思考, 本文将正则化方法引入组合预测模型的加权过程调整每个单项预测模型的权重, 在回归问题(最小二乘估计)中, 正则化一般具有以下形式:

$\min \frac{1}{N}\sum\nolimits_{i = 1}^N {L({\omega _i}{x_i} - {y_i})} + \lambda {(\sum\nolimits_{i = 1}^m {{{\left| {{\omega _i}} \right|}^p}} )^{\frac{1}{p}}}$

(7)

式(7)被称作代价函数, 其中, N表示数据集的样本总量, m表示需要被加权的特征总量, ${\omega _i}$ 表示权重系数矩阵, ${x_i}$ 表示权重系数矩阵对应的样本特征的向量, 加号前是损失函数, 加号是正则化项, λ为调整两者之间的关系的系数, 一般称之为正则项系数, 常用的正则项有两种: L₁范数正则化和L₂范数正则化.

1) L₁范数正则化

L₁范数得名原因是因为式(7)中正则化项的p取值为1, 即正则化项为 $\lambda \displaystyle\sum\nolimits_{i = 1}^n {\left| {{\omega _i}} \right|} $ , 其中的 $\displaystyle\sum\nolimits_{i = 1}^n {\left| {{\omega _i}} \right|} $ 就是L₁范数, 一般写作 $\left\| {{\omega _i}} \right\|$ .

在一般的最小二乘加权模型中, 模型会通过最小化平方误差和来选择权重, 在这个过程中模型只会注重误差平方和最小化而忽略了对权重的控制, 将L₁范数加入最小化函数中后, 如果对单个模型赋予的权重过大, 最小化函数仍然无法实现最小化, 这就会使得模型在选择权重时有两个方面的考虑: 误差平方和最小化和权重系数矩阵最小化.

将L₁范数代入本文的组合预测模型中, 得到基于L₁范数的组合预测模型的代价函数:

$\min f(\omega ) = \frac{1}{n}\sum\nolimits_{t = 1}^n {{{\left( {\sum\nolimits_{i = 1}^J {{\omega _i}{e_i}(t)} } \right)}^2}} + \lambda \left\| {{\omega _i}} \right\|$

(8)

2) L₂范数正则化

与L₁范数类似, L₂范数得名原因是由于式(7)中正则化项的p取值为2, 即为 ${\left( {\displaystyle\sum\nolimits_{i = 1}^m {\left| {{\omega _i}} \right|^2} } \right)^{\frac{1}{2}}} \!=\!\sqrt {\displaystyle\sum\nolimits_{i = 1}^m {{{\left| {{\omega _i}} \right|}^2}} } \! =\! $ $ {\left\| {{\omega _i}} \right\|^2}$ , L₂范数与L₁范数的工作原理类似, 都是在最小化损失函数的过程中降低权重系数矩阵的值, 但是达到的效果有所不同, 具体见图1.

如图1所示, 图左是L₁范数, 图右是L₂范数, 旋涡部分代表损失函数最小化的过程, 在整体代价函数最小化的过程中, L₁范数的图像与权重 ${\omega _i}$ 的图像在零点以外的地方只会无限接近不会重合, L₂范数的图像与权重 ${\omega _i}$ 的图像则有可能在零点以外的地方重合; 这意味着L₁范数可能会使部分权重变为0, 而L₂范数则只会让每个特征尽可能的变小而不会变为0.

将L₂范数代入本文的组合预测模型中, 得到基于L₂范数的组合预测模型的代价函数:

$\min f(\omega ) = \frac{1}{n}\sum\nolimits_{t = 1}^n {{{\left( {\sum\nolimits_{i = 1}^J {{\omega _i}{e_i}(t)} } \right)}^2}} + \lambda {\left\| {{\omega _i}} \right\|^2}$

(9)

这样就得到了带有正则化项的组合预测模型:

$\begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {\min f(\omega ) = \dfrac{1}{n}\displaystyle\sum\nolimits_{t = 1}^n {{{\left( {\sum\nolimits_{i = 1}^J {{\omega _i}{e_i}(t)} } \right)}^2}} + \lambda {{\left\| {{\omega _i}} \right\|}^p},p \in \{1,2 \}} \\ {{\rm {s.t.}}\displaystyle\sum\nolimits_{i = 1}^J {{\omega _i} = 1} } \end{array}} \right. \\ {\varPhi _t} = {\omega _1}{\varphi _1}(t) + {\omega _2}{\varphi _2}(t) + \cdots + {\omega _J}{\varphi _J}(t) = \displaystyle\sum\nolimits_{i = 1}^J {{\omega _i}{\varphi _i}(t)} \\ \end{array} $

(10)

基于正则化的组合模型在为单项预测模型加权的过程中, 就不会出现因为某个单项预测模型在训练数据上表现过好或过差而为其赋予很大的权值, 避免了组合预测模型在预测数据上表现出“过拟合”的情况.

(3) 交叉验证

交叉验证是机器学习中另一种选择模型、优化模型的方法, 常用于数据量对于拟合模型不是很充足的时候, 其思想是重复的使用数据, 把给定的数据进行切分, 将切分的数据集分为训练集和测试集, 在这个基础上反复进行训练、测试以及模型选择. 交叉验证方法包括简单交叉验证、K折交叉验证和留一交叉验证.

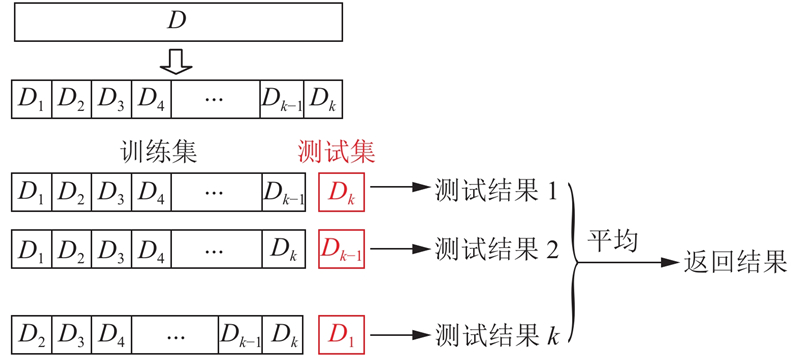
如图2所示, K折交叉验证的思想是将已给数据切分为K个大小相同、互不相交的子集, 利用其中K–1个子集进行训练, 剩下的一个子集用来测试模型, 这种操作重复进行K次, 最后选择在K次评测中误差最小的模型; 留一交叉验证是是K=N时的K折交叉验证, 这种方法往往在数据量较小的情况下使用, 本文所使用的数据量相对于较小, 故选用留一交叉验证.

(4) 模型优劣判定

本文将把总数据集分为训练集和测试集, 总样本量设为N, 训练集容量为m, 选用平均绝对百分比误差MAPE对测试集上的模型预测结果进行评价:

$MAPE = \frac{1}{{N - m}}\sum\nolimits_{t = m + 1}^N {\left| {\frac{{{\varPhi _t} - {x_t}}}{{{x_t}}}} \right|} $

(11)

2 实证分析 2.1 数据说明

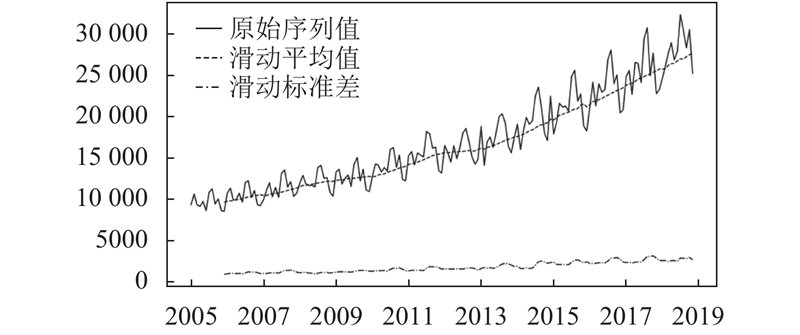
为了保证正则化和交叉验证有一定的学习率, 本文在一定程度上扩大了时间序列的数据量, 采用的时间序列数据为我国铁路客运量2005年1月~2018年11月的月度数据, 样本量为168, 数据来源为国家统计局, 时间序列趋势图如图3.

如图3所示, 我国铁路客运量有明显的升高趋势和周期性趋势, ADF检验表明数据存在不稳定性, 是不平稳序列, 适合使用SARIMA模型和Holt-Winters模型进行时间序列预测.

2.2 单项预测模型选择

根据自相关和偏自相关图、AIC准则、模型显著性以及实验数据序列周期性与时间的相关性, 本文使用的单项预测模型如下:

1) SARIMA(1,1,1)(1,1,1)[12]模型;

2) SARIMA(1,1,1)(0,1,1)[12]模型;

3) SARIMA(0,1,1)(0,1,1)[12]模型;

4) Holt-Winters累加模型.

另外, 以上3个SARIMA模型的AIC值接近, 参数只有一个未通过检验但是非常接近给定的P值,

为了保留可能存在的潜在信息, 对这3个SARIMA模型的预测结果都予以保留.

2.3 组合预测模型

本文选用的组合预测模型如下:

1)最小二乘法组合模型;

2)基于L₁范数的组合模型 $\left( {\lambda = 1} \right)$ ;

3)基于L₁范数和交叉验证的组合模型;

4)基于L₂范数的组合模型 $\left( {\lambda = 1} \right)$ ;

5)基于L₂范数和交叉验证的组合模型.

在铁路客运量的组合预测中, 将2005年至2017年的数据作为训练集, 2018年的数据值作为预测集, 计算每个模型在预测集上的误差, 得到模型在测试集上的表现如表1.

由表1所示的各模型在预测集上的预测误差可观察到, 简单最小二乘法组合预测模型的预测误差为3.9576%, 比所有的单项预测模型的预测误差都要低; 引入L₁范数和L₂范数后的组合模型的预测误差分别为3.7993%、3.8118%, 比最小二乘法组合预测模型的预测误差略低; 因此根据实验数据, 说明在组合预测模型进行权重选择时引入正则化项能够使组合预测模型的预测误差降低, 并且基于L₁范数正则的组合模型比基于L₂范数正则的组合模型对组合预测模型的优化效果更好; 此外, 交叉验证在一定程度上改善了L₁范数正则化模型的预测效果, 对L₂范数的模型起到的作用很小, 几乎可以忽略不计.

结合各组合预测模型对单项预测模型的权重选择进行分析, 由表2所示的各组合模型中单项模型的权重, 可发现: 1) 所有的组合模型的权重分布都满足 $\displaystyle\sum\nolimits_{i = 1}^J {{\omega _i} = 1} $ 的条件; 2) 在最小二乘组合模型的权重选择的基础上, 加入L₁范数和L₂范数的单项预测都使其绝对值降低了, 但能够观察到, 加入L₁范数正则的组合模型在调整权重时, 权重绝对值的下降速度更快, 而加入L₂范数正则的组合模型对权重的调整则并不明显.

2.4 实验结论与理论分析

L₁范数是绝对值函数, L₂范数则是二次函数, 这种差异导致L₁范数正则在使模型权重衰减时始终保持同一个速度, 而L₁范数正则会在权重较大时提高衰减速度, 权重较低时降低衰减速度, 最终, L₁范数正则在降低模型复杂度时保留了权重较大的单项模型, 并且尽量使模型变得稀疏, L₂范数正则在降低模型复杂度时则使模型更加符合规则化.

相对于L₂范数正则经常被使用的机器学习特征分配的应用场景, 组合预测模型需要被分配权重的单项预测模型个数较少, 权重数值小, 这使得L₂范数正则在调整组合预测模型的权重时没有L₁范数正则的下降速度快, 改善效果明显.

基于以上分析, 认为L₁范数正则化更适合用于组合预测模型. 另外在实验过程中发现, 参与组合预测的单项预测模型越多, 正则化的改善效果越好.

交叉验证则在一定程度上改善了L₁范数正则化模型的预测效果, 对L₂范数的模型起到的作用很小, L₁范数的代价函数在组合预测模型中表现出的惩罚力度大, 使得交叉验证的改善效果强于L₂范数的惩罚力度, 并且在实验中发现, 训练数据分配的越多, 交叉验证的改善效果就越好.

3 结论

本文按照常规的组合模型设计思路, 在基于最小二乘法的组合预测模型中, 引入了正则化和交叉验证用以优化组合预测模型的权重选择, 通过实验发现: 首先, 组合预测模型优于所有单项预测模型的预测精度, 正则化和交叉验证都能在不同程度改善基于最小二乘法的组合预测模型, 且L₁范数正则化比L₂范数正则化的改善效果更好; 其次, 实验中发现候选的单项预测模型越多、数据量越大, 正则化和交叉验证表现的效果就越好, 因此这种组合预测方法可以推广到基于大数据的多模型组合预测中.