高校教师教学质量评价是提升教学管理水平和教师教学能力的重要途径^[1,2]. 利用教学质量评价, 学生能够反馈教师教学情况, 教师可以反思教学效果, 学校可以有效实施教学管理改进, 有针对性地对教师进行培训. 英语教学是高校教育中的重要一环, 且英语教学质量评价过程较为复杂, 因此构建客观科学的英语教学质量评价模型是一个热点研究方向^[3,4].

针对高校教学质量评价问题, 研究人员提出了多种评价方法, 如灰关联分析法^[5]、层次分析法^[6], 模糊综合评价法^[7]等. 但这些方法适用于线性模型, 难以适应于具有非线性的教学质量评价问题, 存在主观性和随机性缺陷, 不能很好地实现教学质量评价. 为此, 文献[8]构建了一种远程教学质量评价模型, 并基于支持向量机实现教学质量评价, 取得了较好的评价效果. 文献[9]提出了基于智能算法的教学质量评价方法, 利用遗传算法改进BP神经网络评价教学质量, 具有较快的收敛速度和评价精度.

本文研究了高校英语教学质量评价问题, 提出了一种基于遗传算法改进RBF神经网络的教学质量评价方法. 该方法利用RBF神经网络评价英语教学质量, 采用遗传算法优化RBF神经网络的初始权值和径向基参数, 通过主成分分析方法筛选评价指标, 测试结果验证了该方法的有效性和优越性.

1 遗传算法优化RBF神经网络 1.1 RBF神经网络

RBF神经网络的基础是函数逼近理论, 是一种具有很强全局寻优能力的前馈式神经网络, 在信号处理、图像处理以及模式识别领域有着十分广泛的应用^[10]. RBF神经网络通常由输入层、输出层和隐含层组成, 常见结构如图1所示.

RBF神经网络中, 3层神经网络共有2个权值向量, 其中输入层与隐含层的权值为静态权值(固定为1), 输出层与隐含层之间为动态权值, 并且隐含层的激活函数为径向基函数. 因此, 输出层的输出为输入数据通过隐含层激活函数后的加权求和. 径向基函数与动态权值是RBF神经网络的关键, 径向基函数的表达式为:

$R({x_p} - {c_i}) = \exp \left( { - \frac{{{{\left\| {{x_p} - {c_i}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)$

(1)

式中, $\left\| {{x_p} - {c_i}} \right\|$ 表示 ${x_p} - {c_i}$ 的范数, ${x_p}$ 表示输入层输入的样本数据, ${c_i}$ 和 $\sigma $ 分别表示径向基函数的中心和宽度. 确定了网络权值和径向基函数参数后, RBF神经网络的输出可以表示为:

${y_j} = \sum\limits_{i = 1}^h {{\omega _{ij}}} \exp \left( { - \frac{{{{\left\| {{x_p} - {c_i}} \right\|}^2}}}{{2{\sigma ^2}}}} \right),\;\;j = 1,2, \cdots ,n$

(2)

式中, ${\omega _{ij}}$ 表示隐含层与输出的权值. 根据RBF神经网络的求解过程可知, 网络寻优过程就是根据训练数据不断更新动态权值、径向基函数的中心和宽度, 直到整个神经网络实现所需的非线性函数逼近.

应用RBF神经网络实现英语教学质量评价需要预先设定网络的初始权值和径向基函数参数, 初始参数设置对于网络性能具有较大影响. 为提高RBF神经网络英语教学质量评价的准确性和计算效率, 采用遗传算法对RBF神经网络参数进行优化.

1.2 遗传算法

基于RBF神经网络的英语教学质量评价模型在进行训练之前, 采用遗传算法确定最优网络初始参数. 遗传算法通过随机生成多个起始点进行并行寻优, 以适应度函数确定寻优方向, 基于选择、交叉和变异操作实现高维空间自适应快速参数寻优.

(1)染色体编码

RBF神经网络的参数优化是一个连续参数的优化过程, 为了提高参数寻优精确性, 采用浮点数编码方式. 浮点数编码既能够避免后续选择、交叉和变异过程中的编码与解码, 提高收敛效率, 还能够突破传统二进制编码字长的限制, 获得较高的参数寻优精度. 如果构建的RBF神经网络的拓扑解构为4-7-3, 则隐含层到输出层共有21个权值, 隐含层中共需要设置6个径向基函数的中心和宽度, 因此遗传算法的染色体编码长度为33.

(2)适应度函数

针对RBF神经网络参数优化问题, 网络输出值与期望值之差越小, 说明对应的染色体越优. 为此, 采用期望输出与种群中所有个体的均方误差倒数作为遗传算法进化操作的适应度函数, 具体计算方式如下:

$E = \frac{1}{{\displaystyle \sum\limits_{k = 1}^N {{{\left( {{T_k} - {Y_k}} \right)}^2}} }}$

(3)

式中, N表示种群中染色体个数, Y表示模型的实际输出值, T表示模型的期望输出值.

(3)遗传算子

选择操作采用经典的比例选择方法(轮盘赌法), 首先计算每个染色体的个体适应度函数值, 按照适应度函数值的大小对染色体进行排序, 并且规定适应度函数值越大, 对应染色体被选择的概率就越高. 对于染色体 ${b_i}$ , 假设其适应度函数值为 ${E_{{b_i}}}$ , 则其被选择的概率为:

$P({b_i}) = \frac{{{E_{{b_i}}}}}{E}$

(4)

其中, E表示种群中所有染色体的总体适应度函数值. 由式(4)可知, 染色体适应度高低决定了该染色体被选择的概率. 但是, 为了增加种群的多样性以及避免陷入局部最优解, 也需要在适应度较小的染色体中选择一部分遗传入下一代种群.

交叉操作是指遗传算法的进化过程中, 为了增加种群的多样性, 对两个染色体的编码按照一定规则进行部分基因位的交换, 最终进化出两个新的染色体的过程. 在遗传算法寻优过程中, 绝大多数新染色体均是由交叉操作得出的, 交叉操作是遗传寻优的核心. 遗传进化早期, 染色体个体的适应度函数值较小, 需要对染色体进行大概率交叉操作, 以提高遗传算法的全局寻优能力. 遗传进化后期, 多次选择交叉变异操作已经使得染色体个体的适应度函数值较大, 此时应该以较小的概率进行交叉操作, 以提高算法的局部寻优能力. 为此, 文中遗传进化中交叉概率设置为:

${P'_c} = \left\{ \begin{aligned} & {P_{c\max }},\;{E_{\max }} < {E_{\rm{mean}}} \\ & {P_{c\max }} - \frac{{{P_{c\max }} - {P_{c\min }}}}{{ite{r_{\max }}}} \end{aligned} \right. \times iter,\;{E_{\max }} \ge {E_{\rm{mean}}}$

(5)

式中, ${E_{\max }}$ 表示父代种群中两个待交叉染色体的最大适应度函数值, ${E_{\rm{mean}}}$ 表示父代种群中染色体的适应度函数均值, $iter$ 表示遗传进化当前迭代次数, $ite{r_{\max }}$ 表示遗传进化的最大迭代次数, ${P_{c\max }}$ 为预先设定的最大交叉概率值.

变异操作是指在生物进化过程中, 指染色体的某些基因位干扰受到而出现突变, 产生新的染色体个体的过程. 遗传算法进化过程中, 变异也是更新染色体个体, 增加遗传寻优能力的重要环节. 变异概率设置是遗传变异操作的关键, 变异概率较大时有利于遗传算法扩大寻优搜索范围, 获得全局搜索能力, 但不利于保持选择和交叉得出的高适应度染色体个体; 变异概率较小能够有效保存优良染色体个体. 传统遗传算法的变异概率设置为固定值, 通常情况下介于0.001到0.1之间, 这不利于获得优秀染色体. 为此, 参照交叉概率设置方法, 进行变异概率的自适应设置, 变异概率设置方法为:

${P'_m} = \left\{ \begin{aligned} & {P_{m\max }},\;E < {E_{\rm{mean}}} \\ & {P_{m\max }} - \frac{{{P_{m\max }} - {P_{m\min }}}}{{ite{r_{\max }}}} \end{aligned} \right. \times iter,\;E \ge {E_{\rm{mean}}}$

(6)

其中, $E$ 表示父代种群中要进行变异操作的染色体适应度函数值, $iter$ 和 $ite{r_{\max }}$ 分别表示当前迭代次数和最大迭代次数. 式(6)表明, 进化早期染色体适应度函数值低于均值时, 变异概率设置较小, 能够保留优良染色体个体. 随着遗传进化不断进行, 染色体的适应度函数值高于均值时, 可以调高变异概率, 增加遗传算法的局部寻优能力.

1.3 RBF神经网络参数优化模型

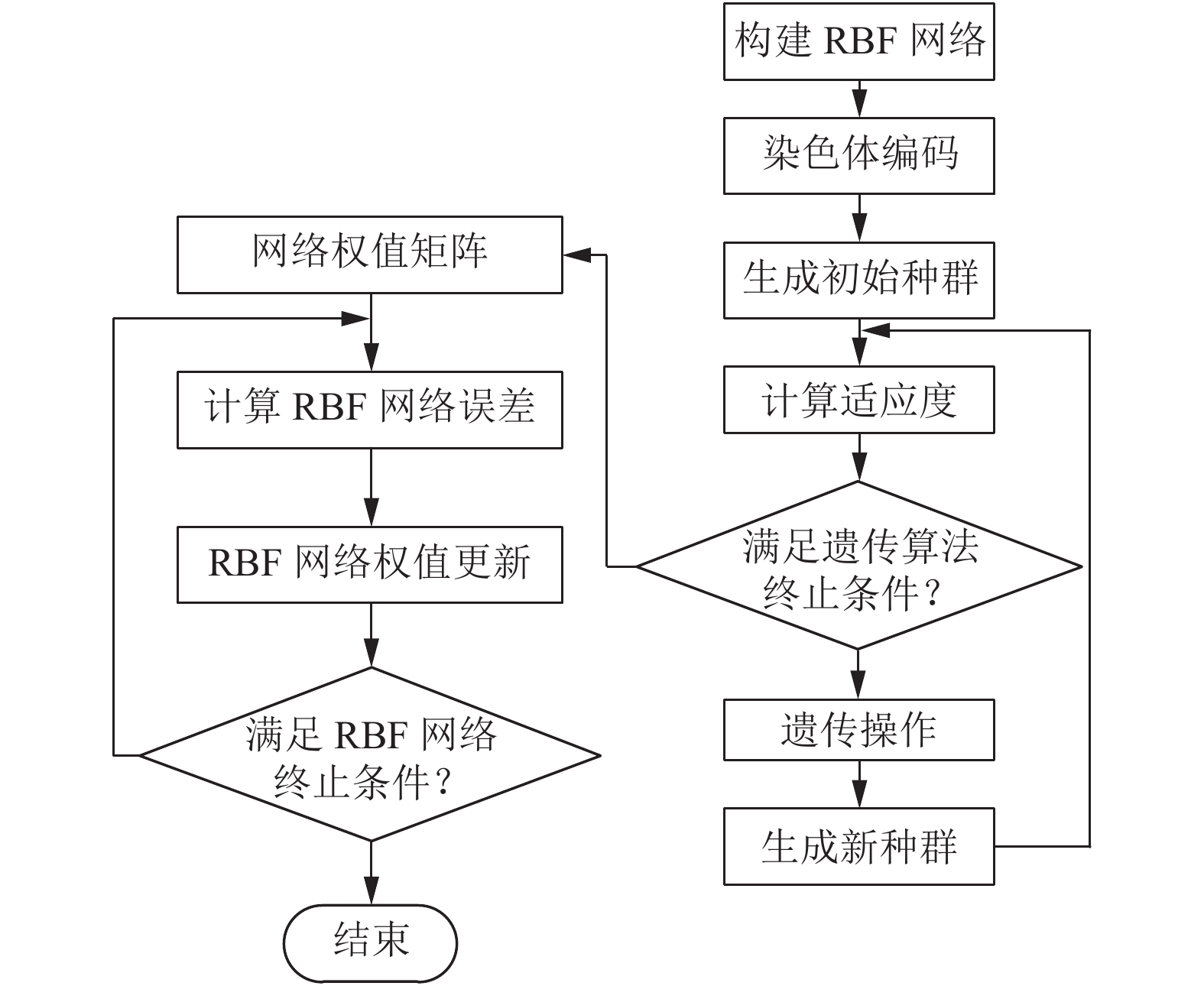
遗传算法能够对RBF神经网络的动态权值、径向基函数的中心和宽度进行优化. 针对英语教学质量评价问题, 基于遗传算法优化的RBF神经网络结构如图2所示.

2 评价指标主成分分析

目前, 用于英语教学质量评价的指标众多, 如果不加选择直接将这些指标输入到RBF神经网络中, 与教学质量评价相关性较弱或冗余的指标会影响最终评价结果的准确性以及评价效率. 为此, 本节采用主成分分析方法对英语教学质量评价指标进行筛选, 以精简评价指标, 提高英语教学质量评价准确性和实时性.

主成分分析能够对现有英语教学质量评价指标进行综合分析, 去除指标中的冗余成分, 生成教学评价新指标^[11]. 新指标大的降低了数据量, 但能够包含原有指标的绝大部分信息. 指标数量的减少不但能够提高教学质量评价的效率, 还能降低RBF神经网络的复杂程度. 基于主成分分析的教学质量评价具体过程如下.

假设原始英语教学质量评价指标集为:

$X = \left( {{X_1},{X_2}, \cdots ,{X_p}} \right)$

(7)

其中, p为教学评价指标的个数. 英语教学质量评价指标之间的数据差异较大, 为了降低大数据对小数据的影响, 需要对采集数据进行标准化处理, 标准化处理公式为:

${\bar x_{ij}} = \frac{{{x_{ij}} - {{\bar x}_j}}}{{{s_j}}}$

(8)

式中,

$\left\{ \begin{aligned} & {{\bar x}_j} = \frac{1}{n}\sum\limits_{i = 1}^n {{x_{ij}}} \\ & {s_j} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{x_{ij}} - {{\bar x}_j}} \right)}^2}} \end{aligned} \right.$

(9)

教学质量评价指标经过标准化处理后, 计算评价指标的相关系数矩阵:

${{R}} = {\left( {{r_{ij}}} \right)_{p \times p}}$

(10)

其中, ${r_{ij}}$ 表示第i个教学质量评价样本与第j个指标的相关系数, 计算方式为:

${r_{ij}} = \frac{1}{{n - 1}}\sum\limits_{k = 1}^n {{{\bar x}_{ki}}{{\bar x}_{kj}}} $

(11)

构建特征方程 $\lambda u = {{R}}u$ , 并计算特征方程的特征值和特征向量:

$\lambda = \left( {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _p}} \right),\;{\lambda _1} \ge {\lambda _2} \ge \cdots \ge {\lambda _p} \ge 0$

(12)

$u = \left( {{u_1},{u_2}, \cdots ,{u_p}} \right)$

(13)

计算英语教学质量评价指标主要成分对累计方差的贡献量:

$\zeta = \sum\limits_{i = 1}^P {{\alpha _i}} $

(14)

式中, ${\alpha _i}$ 代表教学质量评价指标中第i个主要成分的贡献. 为了从教学质量评价指标中选取最能代表全部指标信息的主要指标(即主成分), 如果前m个主要成分的累计贡献大于85%, 可以认定这m个主要成本能够基本代表全部的英语教学质量评价指标. 基于主成分分析选定的指标作为新的评价评价英语教学质量的特征向量, 能够在保持教学质量评价性能不变的同时, 有效降低特征的维度, 提高评价效率.

3 英语教学质量评价模型

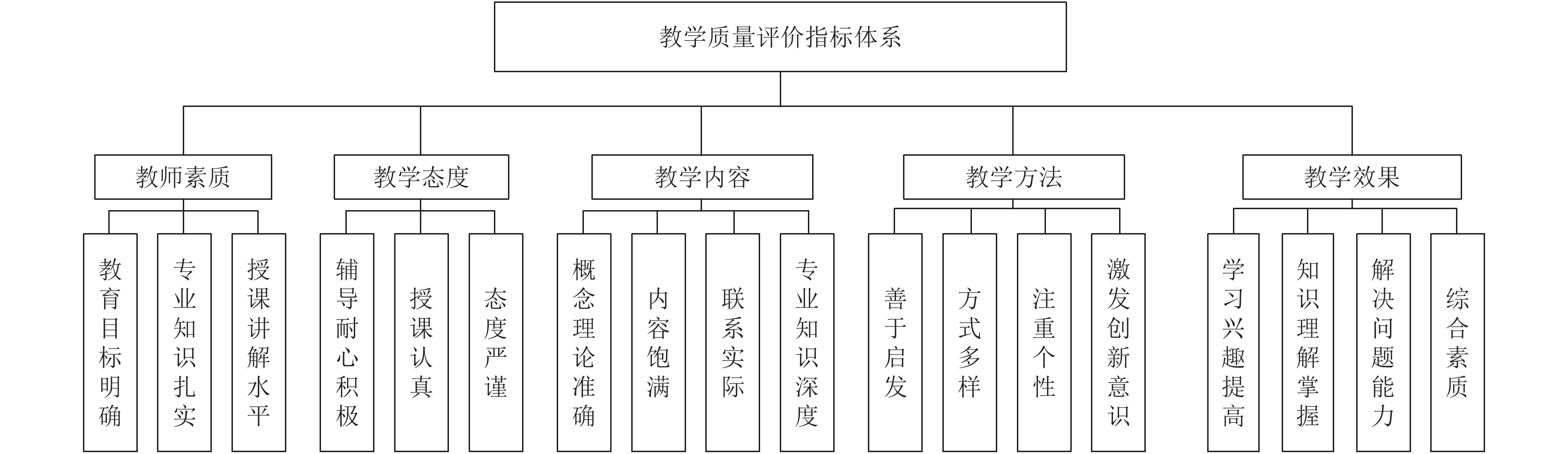
评价指标体系是英语教学质量评价的基础, 科学合理的指标体系是保证教学质量评价性能的有力保障. 目前, 评价教学质量的指标体系有多种原则, 例如基于教学内容的指标构建, 基于学生成绩的指标构建等. 针对英语教学质量评价问题, 本文构建了具体的评价指标体系, 结构如图3所示.

本文提出的基于RBF神经网络的英语教学质量评价流程如下:

步骤1. 构建评价指标体系, 收集教学质量评价相关数据;

步骤2. 数据标准化处理, 生成评价指标相关系数矩阵;

步骤3. 基于主成分分析对英语教学质量评价指标进行选择, 去除冗余指标, 实现特征降维;

步骤4. 利用遗传算法改进的RBF神经网络进行教学质量的评价, 输出评价结果.

4 模型测试与分析

为测试本文提出的基于遗传算法优化的RBF神经网络英语教学质量评价方法的有效性, 本节利用收集到的高校英语教师教学质量评价数据对其进行性能测试. 按照上一节构建的英语教学质量评价指标模型, 共采集了400组英语质量评价数据, 其中360组作为训练数据, 剩余40组作为测试数据, 部分采集数据如表1所示, 表中x₁~x₁₈依次对应图3中的教学质量评价指标.

4.1 主成分分析选择评价指标

利用提出的英语评价指标主成分分析法对表1中的英语教学质量评价指标进行分析, 筛选出对教学质量评价贡献度最大的指标, 主成分分析结果如图4所示.

图3结果表明, 前8个主成分指标对英语教学质量评价的累积贡献率已经高达94.3%, 超过了设定的累积贡献率门限. 这表明前8个指标已经能够有效代表全部指标中包含的重要信息, 后续将采用这8个指标对英语教学质量进行评价.

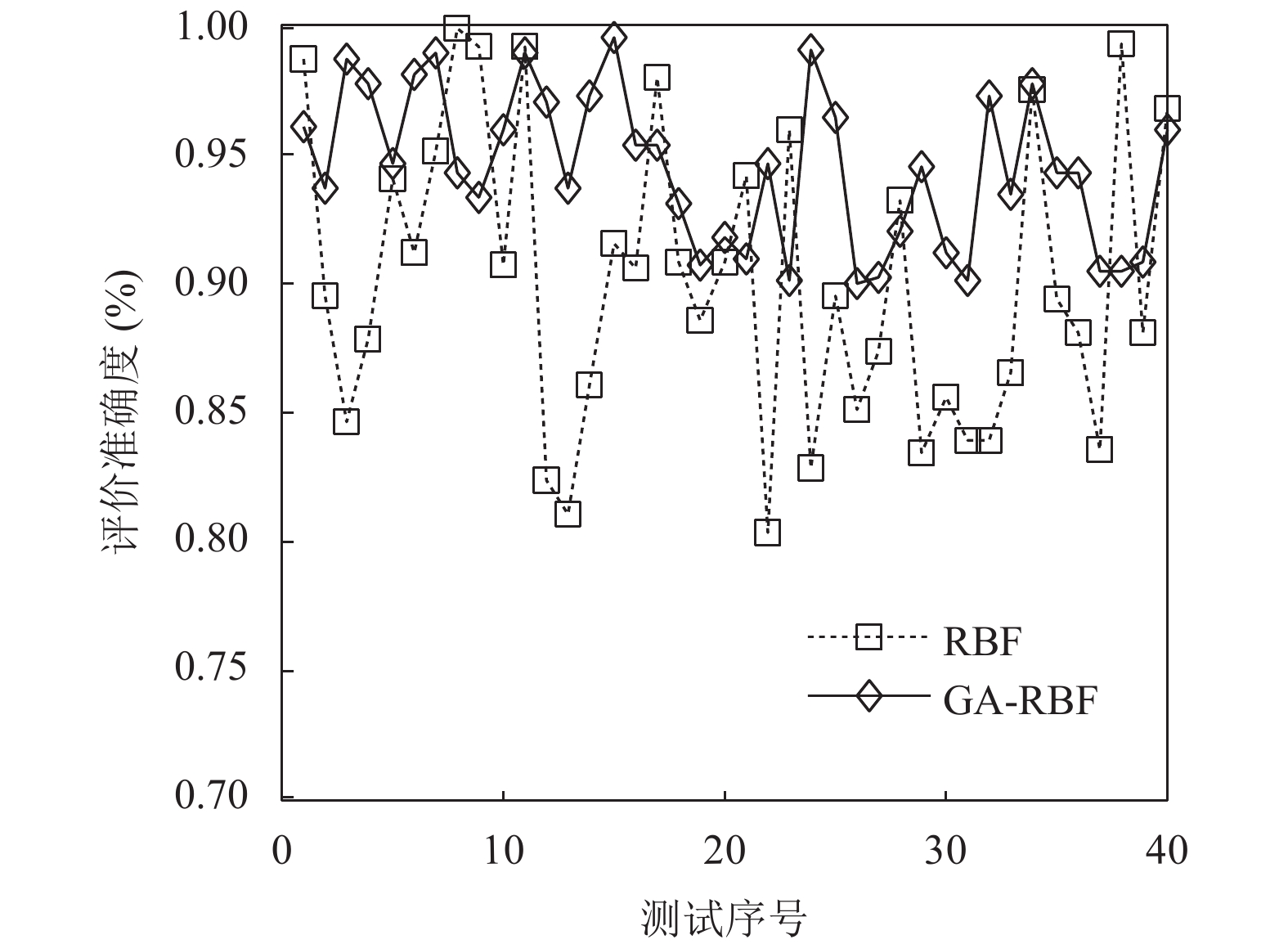
4.2 教学质量评价结果分析

采用本文构建的遗传算法优化RBF神经网络模型对英语教学质量进行评价, 模型训练过程中均方误差变化曲线如图5所示, 测试组数据的教学质量评价精度如图6所示. 图5表明, 原始RBF神经网络经过约45次迭代达到收敛, 而经过遗传算法优化后只需约30次即可达到收敛, 这表明遗传算法能够有效提升RBF神经网络的收敛速度, 降低模型训练时间. 并且, 经过遗传算法优化后的RBF神经网络的军方误差也始终低于原始RBF神经网络, 表明遗传算法能够提升模型的预测准确性.

图6表明, 原始RBF神经网络对英语教学质量评价精度较高, 均高于81%, 但遗传算法优化RBF神经网络的评价精度优于原始RBF神经网络. 统计结果表明, 在40组测试样本中, 遗传算法优化RBF神经网络模型对36组评价准确度均大于90%, 且其中30组评价准确度大于93%, 表明了模型具有很高的逼近精度.

4.3 评价结果对比分析

为进一步测试本文构建的基于遗传算法优化RBF神经网络英语教学质量评价性能, 将其与文献[9]提出的GA-BPNN评价模型和文献[8]提出的基于支持向量机(SVM)的评价模型进行性能对比测试. 仿真数据不变, 英语教学质量评价性能对比如表2所示. 实验结果表明, 本文构建的遗传算法优化RBF神经网络模型具有较高的评价准确度和运算效率. 这是因为文献[9]的GA-BPNN评价模型中BP神经网络存在过拟合现象, 影响评价准确性, 文献[8]的SVM评价模型中评价指标过多, 指标之间互相干扰, 影响评价准确性的同时也增加了运算成本.

5 结论

高校英语教学质量评价是提升教学质量的重要措施, 本文构建了一种基于遗传算法优化RBF神经网络的英语教学质量评价模型. 该模型利用主成分分析筛选评价指标, 通过遗传算法对RBF网络权值参数进行优化, 实现了英语教学质量的高准确率评价, 测试结果验证了该方法具有较高的评价准确性, 且运算效率较高. 研究内容为高校教学质量评价提供了一种新方法.