2. 西南交通大学 系统可信性自动验证国家地方联合工程实验室, 成都 611756
National-Local Joint Engineering Laboratory of System Credibility Automatic Verification, Southwest Jiaotong University, Chengdu 611756, China
可满足性问题(SATisfiability problem, SAT问题)是判断一个以合取范式(Conjunctive Normal Form, CNF)形式给出的命题逻辑公式, 在多项式时间内是否存在一组真值赋值, 使得该公式为真. 可满足SAT问题, 是世界上第一个被证明的NP-Complete问题[1]. 同时SAT问题被广泛地应用在人工智能、密码系统、计算机科学等实际领域, 因此当前寻找求解SAT问题的有效算法以提升SAT求解技术的健壮性和综合性能极其重要. 近年来很多学者对SAT问题进行了广泛深入的研究, 目前的SAT算法大致可以分为两大类: 完备性算法和不完备算法. 完备性算法采取穷举和回溯思想, 它的优点是能保证找到对应SAT问题的解, 在无解的情况下能给出完备证明, 但不适用于求解大规模的SAT问题. 不完备算法基于局部搜索思想, 在处理可满足的大规模随机类问题时, 往往能比确定性算法更快得到一个解, 但绝大多数随机搜索算法不能判断SAT实例是不满足的.
本文主要介绍完备性算法, 目前流行的完备性算法几乎都是基于DPLL[2]算法衍生而来, CDCL (Conflict-Driven Clause Learning, CDCL)[3]算法是在DPLL算法的基础上添加了高效的启发式分支策略[4]、冲突分析与子句学习机制[5, 6]以及周期性重启[7]等技术, 使得完备算法处理可解决的SAT问题越来越多. 近年来发展出很多冲突驱动型的CDCL求解器, 如Chaff[8]、Zchaff[9]、Minisat[10]、Glucose[11]等, 这些求解器已经在大规模实际领域的问题中得到广泛应用.
本文结构如下: 第1节介绍SAT问题的相关知识; 第2节介绍了几种分支启发式策略; 第3节引出新的决策启发式及其具体算法; 第4节对比测试与实验分析; 最后总结全文.
1 预备知识 1.1 相关定义定义1[12]. 变量集合. 用
定义2[12]. 赋值. 从变量集合
定义3[12]. 文字. 对任意的变量
定义4[12]. 子句. 若干个文字的析取(或,
定义5[12]. 合取范式. 一些子句的合取(与,
(1)布尔约束传播过程(Boolean Constraint Propagation, BCP)
BCP过程也称为单元推导. BCP过程即是反复利用单元子句规则对子句集里的合取范式不断地化简, 直到子句集中不再存在单元子句或者出现冲突子句为止. 随着搜索的不断进行, 一个合取范式想要被满足, 则要求其所组成的子句都是可满足的, 所以通过单元规则会导致一些变量必须被赋值为真(子句中除了一个未赋值的变量外, 其余变量都被赋值为0), 通过单元规则导致的变量赋值被称之为蕴涵[12,13]. 因为子句集中变量的蕴涵关系, 所以BCP过程又可以通过蕴涵图直观地表示出来.
例1. 若有子句集:
| $\begin{aligned} C = \{ &{C_3} = \neg {x_2} \vee {x_{12}},{C_4} = {x_4} \vee \neg {x_{13}}, \\ &{C_5} = {x_6} \vee {x_8} \vee \neg {x_{12}},{C_6} = {x_3} \vee {x_2}, \\ &{C_7} = {x_{10}} \vee \neg {x_6} \vee {x_{13}},{C_8} = \neg {x_2} \vee \neg {x_8} \vee {x_{15}}, \\ &{C_9} = \neg {x_4} \vee \neg {x_6} \vee {x_{11}}, \cdot \cdot \cdot \} \\ \end{aligned} $ |
则可得到蕴含图, 如图1所示.
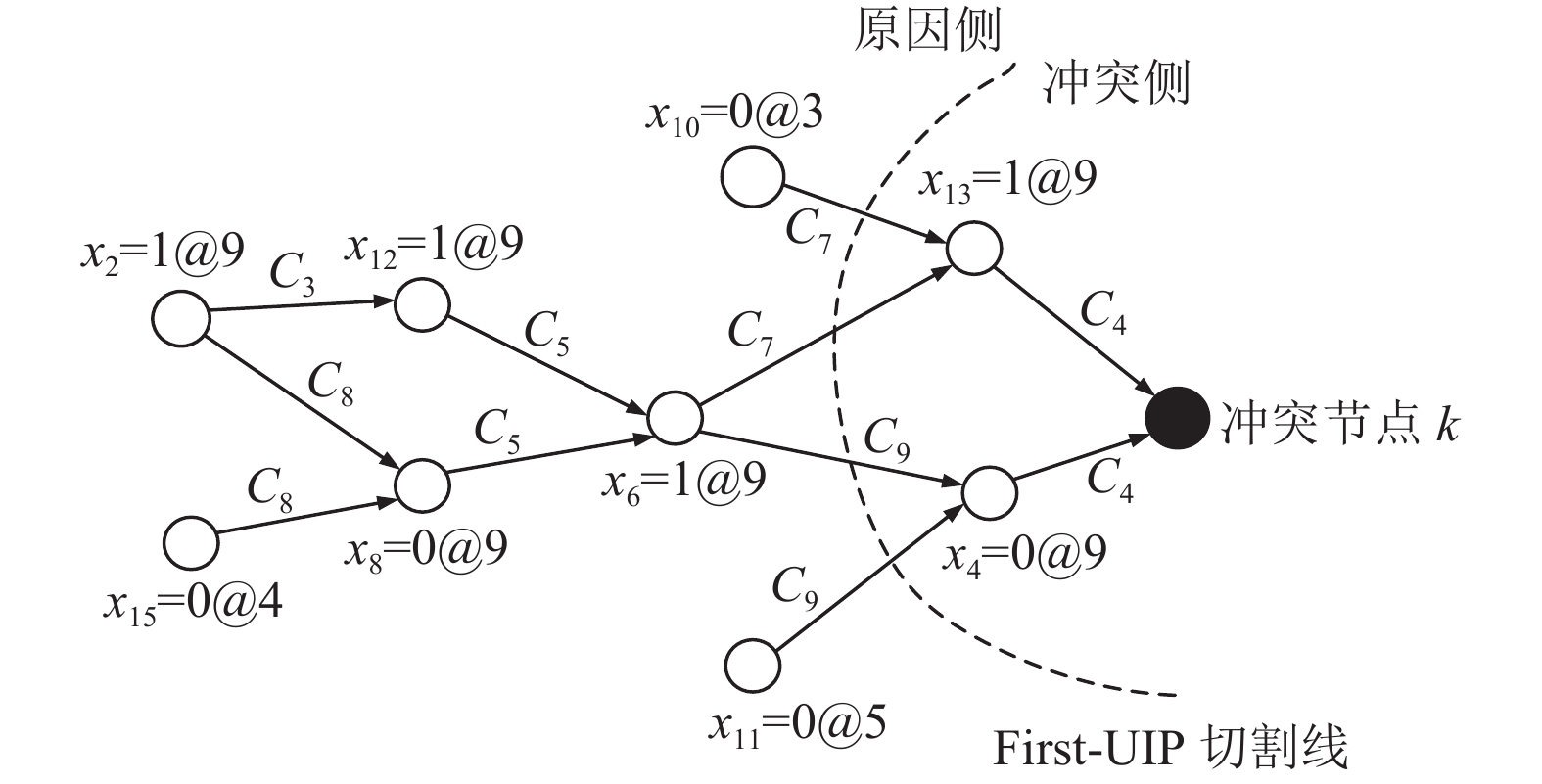
|
图 1 蕴涵图 |
(2)学习子句形成过程
若布尔传播过程中产生冲突, 则求解器进入冲突分析过程, 冲突分析结束后将会产生一个学习子句. 经证明认为, 在冲突分析过程中根据第一唯一蕴含点(First Unit Implication Point, First-UIP)学习得到的子句是最有效的[14]. 根据First-UIP切割方法, 通常把蕴含图被分为两个部分: 冲突侧和原因侧. 如图1所示, 包含冲突节点的一侧为冲突侧, 另一侧为原因侧. First-UIP切割线周围包含了构成此次冲突的所有原因, 学习子句是这些参与冲突分析的子句通过消解规则产生. 图1中参与冲突分析的子句集
Chaff算法表明整个搜索过程中布尔约束传播占用大部分时间, 一个好的分支策略可以快速找到决策变量, 减少冲突次数, 加速BCP过程, 因此好的分支决策对提高整个SAT求解器的运行效率意义重大.
2.1 VSIDS策略VSIDS (Variable State Independent Decaying Sum)分支变量启发式策略, 该策略由Moskewic等于2001年提出[8]. 相比早期的分支启发式, VSIDS分支变量启发式策略很好地结合了冲突分析过程.
(1)每一个变量的正、负文字都分配一个计数器s, 并且初始值设置为0;
(2)当学习子句加入到子句集时, 该子句中所有的文字活性;
(3)每次分支决策时选择计数器分值最高未赋值的文字进行赋值, 在有多个相等计数器的情况下, 随机选择一个文字进行赋值;
(4)所有文字的得分周期性地除以一个常数.
2.2 VSIDS策略的有效变体近年来, 随着SAT问题研究的深入, VSIDS算法得到了不断的改进. NVSIDS (Normalized VSIDS)策略是由Armin等于2008年提出[15]. 该策略为每个变量设置一个计数器, 其中涉及冲突的变量以
ACIDS (Average Conflict-Index Decision Score)[16], ACIDS策略与EVSIDS一样, 对每个变元不区分正负方向, 只保留一个计数器. 变元活跃度累加方式为
除了上述两种分支策略, 目前还发展出一些其他高效的VSIDS的变体策略, 2016 年Liang JH等提出的了CHB (Conflict History Based Branching Heuristic)策略[17]及同年提出的LRB (Learning Rate Branching)策略[18]等. 这些启发式分支策略都是尽可能优先满足学习子句来加速搜索过程, 在很大程度提高了求解速度.
3 基于变量混合特征分支策略上述启发式策略有两方面的优势: (1)仅对参与冲突分析的子句所包含的变量, 即参与冲突分析的变量进行活性更新. 如图1的实例, 变量
我们发现基于冲突分析的活性增长方式并不是完善的, 因为对每个参与冲突分析的变量, 其活跃度的增量是一致的, 没有根据变量的所携带的一些特性来区分变量的重要性, 而在实际求解阶段变量所携带的信息是多方面的, 如: (1)变量的决策层, 在非时序性回溯阶段, 我们认为当回溯到较低的决策层时, 搜素过程对二叉树的剪枝能力越强; (2)变量最近一次参与冲突分析时的总冲突次数, 变量参与冲突分析的冲突差(当前冲突次数-变量最近一次参与冲突分析时的总冲突次数)越小, 我们认为该变量最近越活跃, 可以适当给予更高的活性.
针对此问题, 本文提出了一种基于变量特性的有效混合策略称为混合特征分支策略(Mixed Feature Branching Strategy, MFBS), 此策略不仅加入了变量最近一次参与冲突分析的总冲突次数, 还考虑了参与冲突分析变量所在的原因子句的文字块距离(Literal Block Distance, LBD). LBD值指子句中变量所在的不同决策层数目, Audemard等证明具有较小LBD值的子句比具有较高LBD值的子句更有用[17]. 实际上LBD较小, 则表明子句需要单位传播中的决策数量更少, 子句中的变量分布相对更集中, 更有利于布尔传播过程. 综上, 我们分析了影响变量决策的两个因素, 为了平衡冲突次数与LBD对分支决策影响程度的大小, 我们设置调节因子来适当地平衡分析. 本文的策略具体表述如下:
(1)为每个变量设置一个计数器, 初始为0;
(2)对于参与冲突分析的变量, 活跃度增长方式为
(3)每次分之决策时, 挑选计数器分值最大的为赋值的变量, 作为下一个决策变量. 若多变量值相同, 则随机挑选一个文字赋值.
在步骤(2)的等式中:
| $Hyb(v) = \alpha \frac{{lastconflict}}{{nconflicts}} + (1 - \alpha )\frac{1}{{LBD + 1}}$ |
其中,
算法1. MFBS Branching Heuristic
1. for
2. activity[v] = 0
3. end for
4. loop
5. if a conflict occurs then
6. for
7.
8. end for
9. else
10. unassigned = unsigned variables
11.
12. end if
13. end loop
14. return
Glucose作为国际先进的求解器, 近些年部分优秀的求解器都是在此基础上的改进, 2009年Glucose 3.0获得SAT Main Track组竞赛冠军, 2017年其并行版本求解器Syrup获得冠军等, 本文则选取最新的Glucose4.1求解器为基础, 把MFBS分支策略嵌入Glucose4.1生成Glucose4.1+MFBS版本, 下一步将两版本进行实验对比分析.
4.1 实验环境本文选取的实验机器配置为Windows 64位操作系统, Intel(R) Core(TM) i3-3240 CPU 3.40 GHz 8 GB内存.
4.2 实验方法两个版本的求解器都在4.1的实验配置下, 分别对2017年SAT竞赛Main Track组实进行测试. 2017年实例总体可分为两大类: g2和mp1, 本文首先在每类中随机选取一个小类别共(108个), 其中包括: g2-T(40)、g2-test(2)、g2-UGG(3)、g2-UR(2)、g2-UTI(2)和mp1构成第1步的测试例. 实验第2步选取第1步表现较好的求解器, 对2017年SAT竞赛的350个实例, 进行综合测试. 两个过程中每个实例均限时3600 s, 若超时未解决自动终止.
4.3 实验结果分析本文首先在理论上提出的两个特征因素, 但对于每个特征因素的对分支决策的影响还需要进一步通过实验说明. 因此为了综合评估MFBS算法的求解性能, 充分探究各个特征因素对分支的影响, 本次实验首先对调节因子
图2表示不同版本的4个求解器与原策略对108个实例求解时间对比. 黑色实心三角代表原版求解器, 图中曲线上每个点代表一个实例, 曲线越靠近x轴, 则表明曲线所代表的求解器求解时间越少, 求解个数越多. 从图中可以看出是4个版本中有3个版本的求解时间均优于原版求解器, 其中
| 表 1 Glucose与Glucose4.1+MFBS求解个数对比(108个) |

|
图 2 Glucose与Glucose_4.1+MFBS的求解性能对比 |
为了更深一步探究求解器的性能, 以下的实验, 将针对本文第一步测试的较优的两个求解器:
| 表 2 Glucose与Glucose4.1+MFBS求解个数对比(350个) |
图3列出了两个版本的求解器与原版求解器的求解个数与求解时间的关系, 实心三角代表原版, 空心图形代表MFBS版本. 因MFBS策略倾向于求解可满足性问题, 所以针对2017年350个实例的总体求解时间表现有所减弱. 可以看出前一段实例3个求解器求解时间高度重合, 在中间部分原版求解器的求解性能要高于本文提出的两个版本, 但在求解较难问题时, 本文的两个版本又表现出优于原版的性能, 尤其对于多求解出来的实例, 每个实例用时接近于3600, 因此也会增加总体的平均求解时间.

|
图 3 Glucose4.1与Glucose4.1+MFBS(
|
5 结论与展望
因求解实际的SAT问题的多样性和复杂性, 使SAT问题求解难度提高. 本文所提出的混合启发式策略, 不仅考虑了变量在参与冲突分析的次数, 还加入了变量所在冲突子句的LBD值, 相比传统单一的启发式策略, 具有一定的优势, 测试结果表明混合策略在一定程度上要优于原始策略.
后续将对混合启发式策略进一步测试, 从中探究不同实验参数对整体求解性能的影响, 发现不同因素之间的联系, 进而更好地提高求解器的求解性能.
| [1] |
Cook SA. The complexity of theorem-proving procedures. Proceedings of the Third Annual ACM Symposium on Theory of Computing. New York, NY, USA. 1971. 151–158.
|
| [2] |
Davis M, Logemann G, Loveland D. A machine program for theorem-proving. Communications of the ACM, 1962, 5(7): 394-397. DOI:10.1145/368273.368557 |
| [3] |
Marques-Silva J, Lynce I, Malik S. Conflict-driven clause learning SAT solvers. In: Biere A, Heule M, Van Maaren H, et al, eds. Handbook of Satisfiability. Amsterdam: IOS Press, 2009. 131–153.
|
| [4] |
Marques-Silva J. The impact of branching heuristics in propositional satisfiability algorithms. Proceedings of the 9th Portuguese Conference on Artificial Intelligence. Évora, Portugal. 1999. 62–74.
|
| [5] |
Marques-Silva JP, Sakallah KA. GRASP: A search algorithm for propositional satisfiability. IEEE Transactions on Computers, 1999, 48(5): 506-521. DOI:10.1109/12.769433 |
| [6] |
Audemard G, Simon L. Predicting learnt clauses quality in modern SAT solvers. Proceedings of the 21st International Joint Conference on Artificial Intelligence. Pasadena, CA, USA. 2009. 399–404.
|
| [7] |
Gomes CP, Selman B, Crato N. Heavy-tailed distributions in combinatorial search. Proceedings of the 3rd International Conference on Principles and Practice of Constraint Programming. Linz, Austria. 1997. 121–135.
|
| [8] |
Moskewicz MW, Madigan CF, Zhao Y, et al. Chaff: Engineering an efficient SAT solver. Proceedings of the 38th Design Automation Conference. Las Vegas, NV, USA. 2001. 530–535, doi: 10.1109/DAC.2001.935565.
|
| [9] |
Mahajan YS, Fu ZH, Malik S. Zchaff2004: An efficient sat solver. Proceedings of the 7th International Conference on Theory and Applications of Satisfiability Testing. Vancouver, BC, Canada. 2005. 360–375.
|
| [10] |
Eén N, Sörensson N. An extensible SAT-solver. Proceedings of the 6th International Conference on Theory and Applications of Satisfiability Testing. Santa Margherita Ligure, Italy. 2004. 502–518.
|
| [11] |
Audemard G, Simon L. GLUCOSE: A solver that predicts learnt clauses quality. SAT Competition, 2009. 7–8. http://www.satcompetition.org/2009/.
|
| [12] |
王国俊. 数理逻辑引论与归结原理. 北京: 科学出版社, 2003.
|
| [13] |
张建. 逻辑公式的可满足性判定——方法、工具及应用. 北京: 科学出版社, 2000.
|
| [14] |
Zhang LT, Madigan CF, Moskewicz MH, et al. Efficient conflict driven learning in a Boolean satisfiability solver. Proceedings of the 2001 IEEE/ACM International Conference on Computer Aided Design. ICCAD 2001. IEEE/ACM Digest of Technical Papers. San Jose, CA, USA. 2001. 279–285.
|
| [15] |
Biere A. Adaptive restart strategies for conflict driven SAT solvers. Proceedings of the 11th International Conference on Theory and Applications of Satisfiability Testing. Guangzhou, China. 2008. 28–33.
|
| [16] |
Biere A, Fröhlich A. Evaluating CDCL variable scoring schemes. Proceedings of the 18th International Conference on Theory and Applications of Satisfiability Testing. Austin, TX, USA. 2015. 405–422.
|
| [17] |
Liang JH, Ganesh V, Poupart P, et al. Exponential recency weighted average branching heuristic for SAT solvers. Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. Phoenix, AZ, USA. 2016. 3434–3440.
|
| [18] |
Liang JH, Ganesh V, Poupart P, et al. Learning rate based branching heuristic for SAT solvers. Proceedings of the 19th International Conference on Theory and Applications of Satisfiability Testing. Bordeaux, France. 2016. 123–140.
|
 2020, Vol. 29
2020, Vol. 29



