智能电网的发展推动了用户侧智能电表的普及, 同时各种监控系统的大规模部署使得电网公司能够获得多尺度、全方位的用户用电信息[1], 这些大量、高分辨率的用户负荷数据不但可以用于刻画用户用电习惯, 还可以对用户的用电负荷进行预测, 因此, 挖掘用户负荷数据对于电网系统的调度优化、精细化经营管理以及服务于市场用户等方面具有重要价值[2].
长期以来, 负荷预测是电力系统的研究热点之一. 按照时间期限分类, 电力负荷预测可以划分为长期负荷预测(10年及以上)、中期负荷预测(5年左右)和短期负荷预测. 其中, 长期负荷预测主要用于电力系统未来规划, 短期负荷预测主要是为了合理安排发电机组的启停、减少旋转备用容量, 从而降低发电成本、保障电网的安全稳定性. 根据电力负荷数据时序性和非线性的特点, 短期负荷预测模型一般可以分为两类, 一类是时间序列方法, 通常是将电力负荷看成一种时间序列的集合, 根据电力负荷的历史数据、相关影响因素构建预测模型, 从而实现预测未来负荷值. 常用的方法包括: 傅里叶展开法[3], 指数平滑模型[4], 自回归积分滑动平均模型[5]. 这些传统的时间序列方法对历史数据随时间的平稳性要求比较高, 在一定程度上过于强调对历史数据的拟合, 导致预测精度不高. 另一类是以机器学习为代表的人工智能方法, 主要包括: 统计机器学习方法中的随机森林算法(Random Forest, RF), 支持向量机, 以及深度学习方法中的长短期记忆网络(Long Short Term Memory, LSTM)等. 邹云峰等[6]将数据类进行K-means聚类后分别进行线性回归, 在线损率预测上取得较好结果, 但由于其采用线性回归, 对非线性数据建模能力有限. 黄晗等[7]提出了基于随机森林的方法, 针对历史负荷数据和天气信息对某地区进行预测. 文献[8]将小波变化与极限学习机组合, 提出了一种集成学习预测模型. 以上方法相较于传统的预测方法有了很大的提升, 但难以兼顾到时序数据时间相关性. 文献[9,10]利用了LSTM的时间序列性, 可以更好地预测非稳定状态的负荷数据. 虽然这些方法可以在系统级负荷预测上取得很好的效果, 但由于单个用户用电的波动性和随机性较大, 系统级负荷预测方法在单个用户的负荷预测上的预测性能较差, 无法满足电网精益化管理的需求.
当前短期负荷预测多以电网系统级负荷为研究对象, 而对于用户级对象的研究工作较少. 文献[11]研究了不同内核的支持向量回归(Support Vactor Regers-sion, SVR)模型对单个家庭用电负荷的预测效果. 文献[12]针对呈指数级增长的电力用户数据提出一种改进的并行化的基于随机森林的负荷预测方法. 文献[13]考虑到了用户用电行为的变化, 提出了扩展卡尔曼滤波及核函数极限学习机相结合的方法对用户侧短期负荷进行预测. 文献[14]提出了一种基于决策树和小波去噪相结合的预测方法, 对不同用电模式的用户进行个性化负荷预测. 这些模型考虑了用户用电负荷影响因素, 对不同用户的用电特性进行分析, 但忽略了时间序列相关性对单个用户负荷预测的影响.
从相关工作来看, 对于用户电力负荷预测而言, 需解决两方面问题: 一是如何有效提取与预测目标相关的抽象特征, 以便预测模型学习其中规律; 二是不同用户负荷特点差异较大, 单一预测模型不能对特征差别较大的用户进行负荷预测, 建立组合预测模型以提升预测精度是很有必要的. 因此, 本文从用户负荷数据特性出发, 利用K-means聚类得到不同用户类别, 针对每类用户的负荷数据时间相关性, 搭建不同的负荷预测模型. 为了能够提取与负荷相关的抽象特征, 本文利用不同时间序列信息构建不同张量作为卷积神经网络的输入, 构建出深层卷积网络来预测单个用户的负荷. 最后, 本文结合某地23个用户一年的真实用电负荷数据对本文提出的方法进行验证.
2 基于K-means聚类算法的用户分类图1为随机选择的5个用户的某周负荷曲线图, 不同颜色的曲线表示不同用户的周负荷变化情况. 其中, 横轴表示时刻点, 每15分钟采样一次负荷数据, 纵轴表示负荷数据. 通过观察曲线发现, 对于单个用户而言, 由于生产和经营一般具有较强的周期性和规律性, 其日负荷数据也具有规律性, 具体可以表现为以下2个方面: 如无重大突发情况, 其短时间内负荷曲线波动较小(相邻时刻相关); 不同日的相同时刻的负荷波动差异不大(日相关). 为此, 首先我们利用K-means聚类算法来研究用户用电行为模式.
K-means算法是一种无监督学习方法, 算法通过设定好的中心点对靠近它们的点进行归类, 通过迭代的方式, 逐次更新各聚类中心的值, 直到得到最好的聚类结果. 对处理大数据集而言, K-means聚类算法保持了较高的可伸缩性和高效性. 算法描述如下:
(1)选择合适的k值作为聚类的初始中心点.
(2)计算其他的点到这k个中心点的距离, 离哪个中心点的距离最小就被划分到哪个类. 距离的具体计算公式如下:
| $ d = \sqrt {\sum\limits_{i = 1}^n {{{({x_i} - {y_i})}^2}} } $ | (1) |
(3)通过求平均值的方法更新该类的中心.
(4)按步骤(2)、(3)迭代更新后, 直至各类中心点的值均不再变化, 迭代结束.

|
图 1 某5个用户一周的负荷曲线图 |
本文采用K-means算法对真实数据集中的23个用户的历史数据进行聚类分析, 然后按照其时间序列的不同的相关性, 将不同类别的用户负荷序列转换为张量后输入至不同的卷积神经网络进行抽象特征提取. 聚类得到的结果如表1所示. 其中, A类表示日相关性和相邻时刻相关性均较为明显的用户, B类表示仅相邻时刻相关性较强的用户.
| 表 1 用户聚类结果 |
3 基于CNN特征提取的负荷预测模型 3.1 卷积神经网络
在深度学习的诸多算法中, 卷积神经网络(Convolutional Neural Networks, CNN)因其特殊的网络结构, 在计算机视觉领域应用广泛. 然而, 在电力负荷预测方面的应用较少. CNN的典型网络结构由输入层、卷积层、池化层、全连接层和输出层组成[15]. 其中, 卷积层是CNN的核心, 包括卷积核、卷积层参数和激励函数3个重要部分. 卷积层内部包含多个卷积核, 组成卷积核的每个元素都对应一个权重系数和一个偏差量, 类似于前馈神经网络的一个神经元. CNN的优势在于能够通过较少的权重参数训练提取得到特征[16].
本文采用CNN网络来提取用户历史负荷的特征. 对于A类用户, CNN模型用相邻的前16个负荷数据点和待预测点前16天的相同时刻的数据点分别构造成
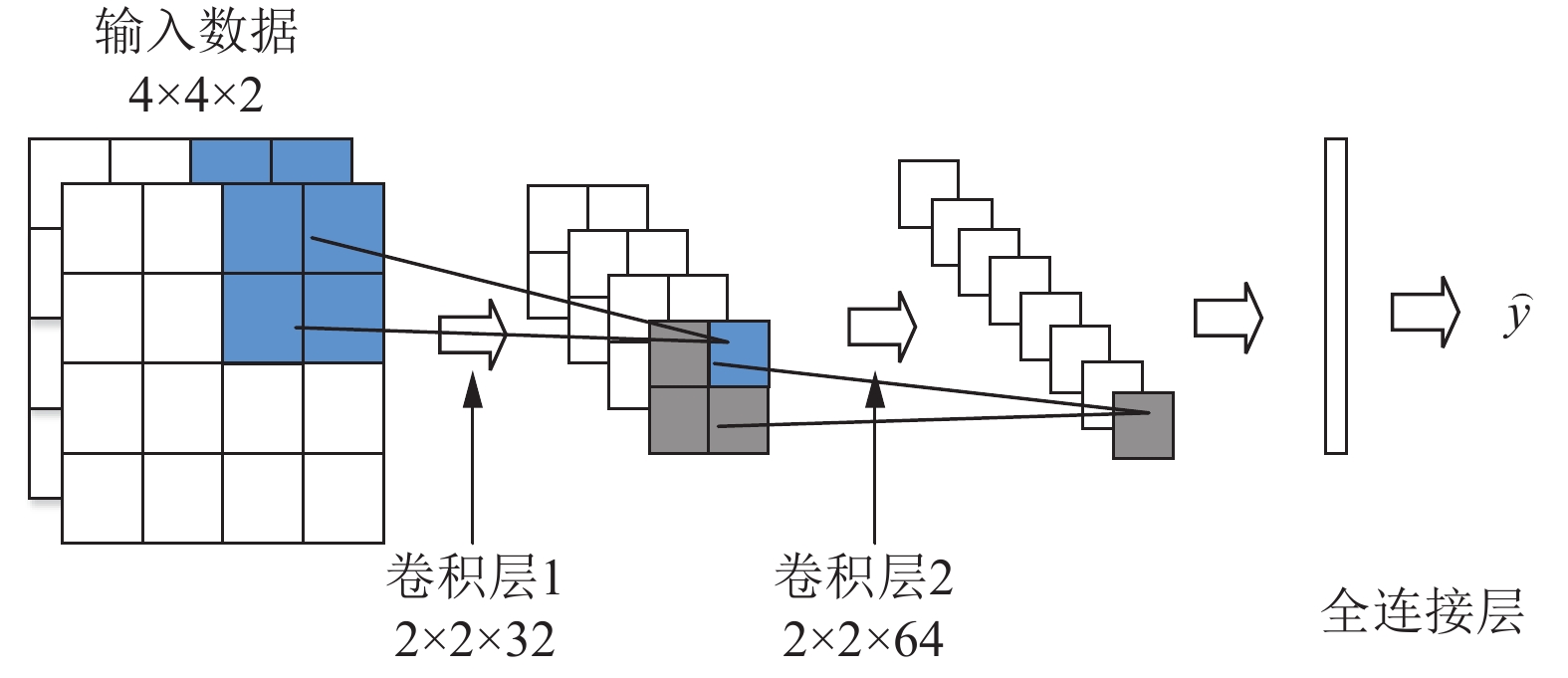
|
图 2 A类用户卷积神经网络结构图 |
对于B类用户, 模型仅以相邻的前16个负荷数据点构建为
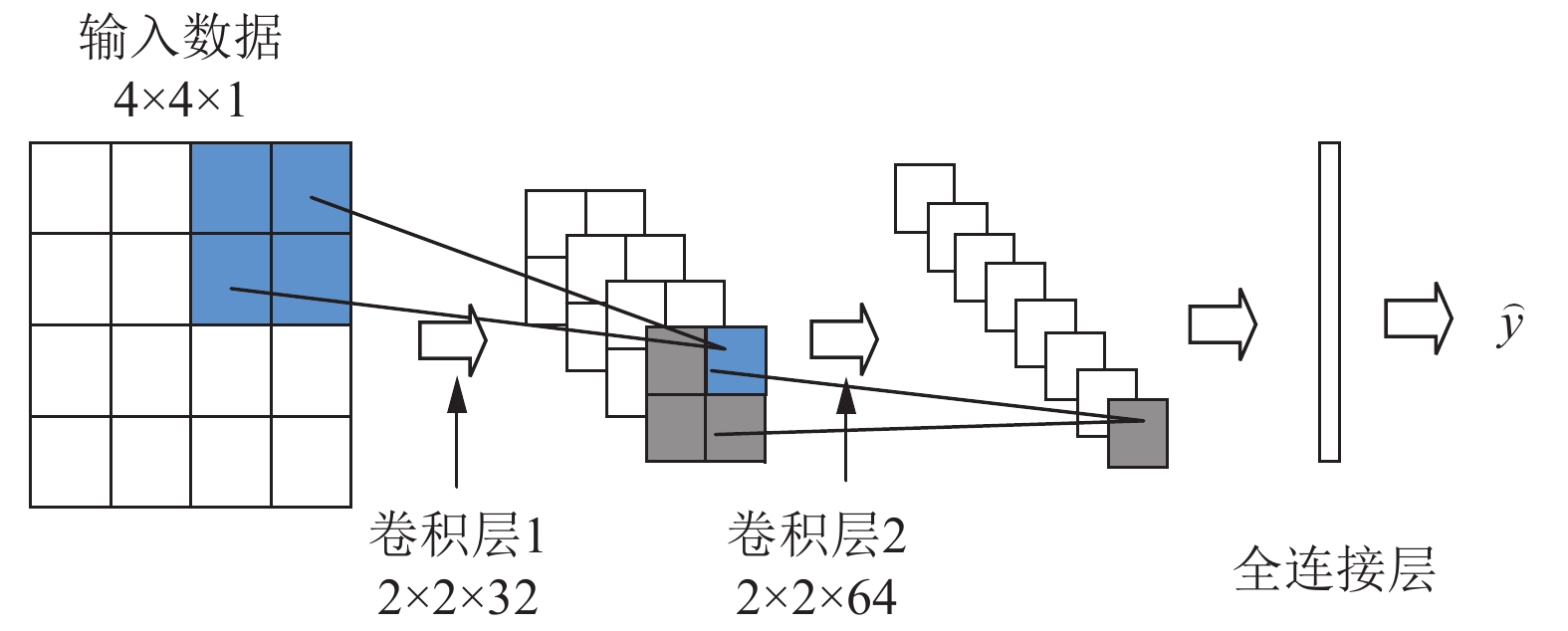
|
图 3 B类用户卷积神经网络结构图 |
考虑到输入数据的维度不高, 因此本文在卷积层后直接接了两个全连接层, 而未使用池化层进行下采样, 保证了数据的完整性. 模型使用ReLU作为激活函数, 选择均方误差(Mean Square Error, MSE)作为损失函数.
3.2 算法流程将历史负荷数据经过数据预处理得到用户用电负荷曲线, 通过K-means聚类将用户分为日相关性强和相邻时刻相关性强的两类用户. 针对不同用户负荷特性, 构建不同张量输入的CNN模型, 具体处理流程如图4所示.

|
图 4 基于K-means和CNN的用户短期电力负荷预测流程 |
4 实验及结果分析 4.1 数据说明与数据预处理
本文所用数据集为某市23个用户2015年全年的负荷数据, 每15分钟采集一个样本点, 每天可获得96个负荷点数据.通过观察数据, 发现原始采集数据存在缺失、数据为负或远大于该用户其他时刻点的负荷数据等失真情况. 因此在用于模型训练和测试前, 本文首先对采集到的负荷数据进行异常处理. 对于缺失或失真的数据, 本文利用该数据的前15个相邻数据点的平均值对其进行填充或修正, 得到完整的负荷数据序列. 同时, 将所有的负荷数据通过归一化映射到[0,1]之间, 公式如下:
| $ x_i^{'} = \frac{{{x_i} - {x_{\max }}}}{{{x_{\max }} - {x_{\min }}}} $ | (2) |
其中,
为了有效评价模型的准确度以及与其他方法进行对比, 本文选取平均绝对误差(Mean Absolute Percentage Error, MAPE)作为评价指标, 计算公式如下:
| $ MAPE = \frac{1}{N}\sum\limits_{i = 1}^N {\left(\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|*100\% \right)} $ | (3) |
其中,
采用本文提出的CNN算法对经过K-means算法分类的电力用户进行负荷预测, 训练集与测试集划分比例为8:2. 训练集采用的是2015年1月1日至2015年10月15日的数据, 共有28 128条记录; 测试集采用的是2015年10月15日至2015年12月31日的数据, 共有7007条记录.
(1)将本文模型与随机森林和支持向量回归机进行比较, 结果见表2.
| 表 2 不同电力负荷预测方法MAPE比较(%) |
本文模型对绝大多数用户的预测效果都优于现有算法, 平均MAPE为30.91%, 相对于现有最好的RF方法MAPE降低了20%, 说明本文模型可有效提高短期负荷的预测准确度. 其中user5的准确度相较其他模型提高得最多, 因为user5的数据波动很大, 通过归一化可以增加数据的稳定性, 提高预测的准确度. 由表2可见, 不同用户的MAPE差距很大, 这是因为不同用户的用电行为习惯差异很大.
图5为user1和user8在2015年1月1日至2015年2月28日的负荷曲线. 图5中, user1历史负荷曲线较平稳, 其用电模式较规律, 因此可得到较准确的预测结果, 而user8在同段时间的用电行为模式难以捕捉, 无法达到较好的预测效果. 这说明了针对不同用户采用不同预测模型的有效性和重要性.
(2)为了验证聚类方法的有效性, 将本文模型与仅输入相邻时刻相关的CNN模型、输入相邻时刻序列和日相关特征序列的CNN模型进行比较, 结果如表3所示.
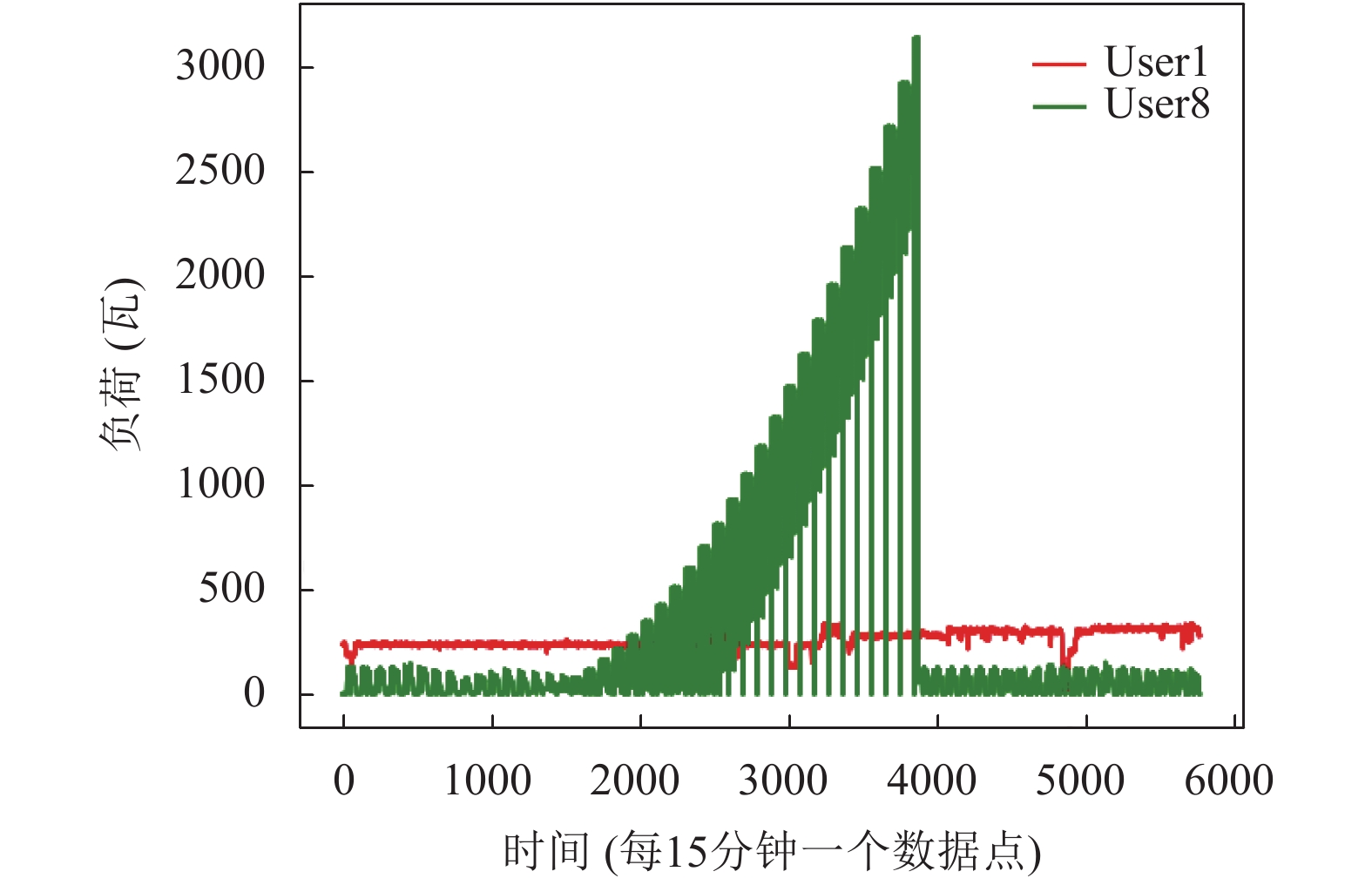
|
图 5 user1和user8 2015年1月1日至2015年2月28日负荷曲线 |
| 表 3 聚类效果MAPE分析(%) |
从表3不难看出, 本文模型的MAPE比简单将数据放入CNN模型的MAPE降低了5%, 证明了应用聚类算法可更好区别不同用户的特性, 有助于提高预测性能.
5 结论针对用户负荷差异明显、波动性大的问题, 本文利用K-means算法将用户用电历史负荷曲线进行聚类, 针对不同类别的用户利用CNN构造不同的特征提取网络结构, 训练建立预测模型. 实验结果表明本文模型均比RF、SVR及未经聚类的CNN模型的预测效果优秀, 预测MAPE降低了21.22%. 由于当前预测模型仅参考了用户的历史负荷作为模型输入, 实际上用户负荷与温度、湿度及用户所在行业经济形势等多种因素相关, 后续将考虑筛选更多的相关因素输入模型中, 进一步提高模型的预测准确度.
| [1] |
王继业, 季知祥, 史梦洁, 等. 智能配用电大数据需求分析与应用研究. 中国电机工程学报, 2015, 35(8): 1829-1836. DOI:10.13334/j.0258-8013.pcsee.2015.08.001 |
| [2] |
马天男, 王超, 彭丽霖, 等. 多源异构大数据下综合能源系统用户用能行为预测分析研究. 智慧电力, 2018, 46(10): 86-95. DOI:10.3969/j.issn.1673-7598.2018.10.014 |
| [3] |
Beiraghi M, Ranjbar AM. Discrete Fourier transform based approach to forecast monthly peak load. Proceedings of 2011 Asia-Pacific Power and Energy Engineering Conference. Wuhan, China. 2011. 1–5.
|
| [4] |
史文博, 王健, 沈添福, 等. 基于改进倍比平滑法的节假日短期负荷预测方法. 电力建设, 2014, 35(10): 21-25. DOI:10.3969/j.issn.1000-7229.2014.10.005 |
| [5] |
Hor CL, Watson SJ, Majithia S. Daily load forecasting and maximum demand estimation using ARIMA and GARCH. Proceedings of 2006 International Conference on Probabilistic Methods Applied to Power Systems. Stockholm, Sweden. 2006. 1–6.
|
| [6] |
邹云峰, 梅飞, 李悦, 等. 基于数据挖掘技术的台区合理线损预测模型研究. 电力需求侧管理, 2015, 17(4): 25-29. DOI:10.3969/j.issn.1009-1831.2015.04.006 |
| [7] |
黄晗, 孙堃, 刘达. 基于随机森林的电力系统小时负荷预测研究. 智慧电力, 2018, 46(5): 8-14. DOI:10.3969/j.issn.1673-7598.2018.05.002 |
| [8] |
Li S, Goel L, Wang P. An ensemble approach for short-term load forecasting by extreme learning machine. Applied Energy, 2016, 170: 22-29. DOI:10.1016/j.apenergy.2016.02.114 |
| [9] |
Muzaffar S, Afshari A. Short-term load forecasts using LSTM networks. Energy Procedia, 2019, 158: 2922-2927. DOI:10.1016/j.egypro.2019.01.952 |
| [10] |
Zheng J, Xu CC, Zhang Z, et al. Electric load forecasting in smart grids using Long-Short-Term-Memory based recurrent neural network. Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems. Baltimore, MD, USA. 2017. 1–6.
|
| [11] |
Aurangzeb K. Short term power load forecasting using machine learning models for energy management in a smart community. Proceedings of 2019 International Conference on Computer and Information Sciences. Sakaka, Saudi Arabia. 2019. 1–6.
|
| [12] |
王德文, 孙志伟. 电力用户侧大数据分析与并行负荷预测. 中国电机工程学报, 2015, 35(3): 527-537. DOI:10.13334/j.0258-8013.pcsee.2015.03.004 |
| [13] |
汤庆峰, 刘念, 张建华, 等. 基于EMD-KELM-EKF与参数优选的用户侧微电网短期负荷预测方法. 电网技术, 2014, 38(10): 2691-2699. DOI:10.13335/j.1000-3673.pst.2014.10.012 |
| [14] |
罗敏, 程将南, 王毅, 等. 基于小波去噪和决策树的个性化大用户负荷预测. 南方电网技术, 2016, 10(10): 37-42. DOI:10.13648/j.cnki.issn1674-0629.2016.10.006 |
| [15] |
周飞燕, 金林鹏, 董军. 卷积神经网络研究综述. 计算机学报, 2017, 40(6): 1229-1251. DOI:10.11897/SP.J.1016.2017.01229 |
| [16] |
Huang CJ, Kuo PH. A deep CNN-LSTM model for particulate matter (PM2.5) forecasting in smart cities
. Sensors, 2018, 18(7): 2220. DOI:10.3390/s18072220 |
 2020, Vol. 29
2020, Vol. 29



