由于资源消耗和环境影响, 可持续性成为工业界的一个重要课题. 其中, 能源消耗和碳排放是制造业在绿色条件下运作的两个主要问题. Garetti等^[1]指出制造业占世界能源消耗的33%, 碳排放总量的38%以上. 随着阴极射线管(CRT)被平板显示器取代, 薄膜晶体管液晶显示器(TFT-LCD)面板在监控设备、液晶电视、移动电话和平板个人电脑等领域广泛应用, 其需求迅速增长. 与其他平板显示类产品^[2]相比, 10英寸TFT-LCD及以上产品的年销售总量占全球的50%以上. TFT-LCD产品在生产过程中消耗大量的能源, 电力约占75%, 其中, 机器运转所消耗的电力占45~50%^[3]. 因此, 如何通过生产调度, 有效降低TFT-LCD产品生产过程中的能源消耗和碳排放量, 达到节能减排显得尤为重要.

在TFT-LCD生产调度研究领域, 阵列工艺(array)阶段包含大量可重入制造工艺, 面板工艺(cell)阶段包含大量并行机工艺, 模块工艺(module)阶段可以看作柔性作业车间问题. 在array阶段, Choi等^[4]提出了一种具有决策树的实时调度机制, 它消除了通过仿真运行选择调度规则所需的计算负担. Hong等^[5]提出一种两相解码遗传算法, 以最大限度地利用光刻阶段, 提高了机器利用率和生产系统的能力. 在cell阶段, Lin等^[6]在考虑批量释放时间的同时也考虑了调度规则的影响, 并提出一种基于批量释放时间的启发式算法和基于队列时间最大不匹配的摩擦机调度规则, 提高了cell阶段的生产效率. Wu等^[7]建立了一种DBR定制模型, 并提出了一种利用转鼓缓冲绳(DBR)系统对cell阶段进行调度控制的方法, 提高了cell阶段的生产效率. 徐峰等^[8]以最小化最大完工时间和交货期最短为目标函数, 使用精英保留和贪婪解码相结合的遗传算法进行求解, 缩短了cell阶段的生产时间. 吴思思等^[9]以最小化最大完工时间、机器等待时间和交货期为目标, 使用布谷鸟算法进行求解, 并首次在cell阶段引入学习退化效应, 分析了学习退化效应对调度结果的影响. 在module阶段, Chou等^[10]提出一种多目标混合遗传算法来解决TFT-LCD模块装配的调度问题, 该问题是一种柔性作业车间调度问题: 力求在满足客户需求的同时, 最大限度地减少制造时间和机器加工准备时间.

绿色调度通过对资源的合理分配和优化工件排序, 以达到增效、节能、减排、降耗的目的, 提高经济效益的同时实现制造过程的绿色化^[11]. 在绿色调度研究领域, 针对并行机调度问题, Cataldo等^[12]在计算总能耗时适当考虑不同路径移动待加工零件所需的能耗, 并采用模型计算最优控制行为, 以限制总能耗, 使整体产量最大化. Wang等^[13]提出一种两阶段启发式求解并行机调度问题的方法, 该方法的目标是使最大完工时间最小. Ji等^[14]提出了一种新的粒子群优化算法, 在最大完工时间在不超过一定水平的情况下, 使资源消耗最小化. Li等^[15]提出了一种基于LPT规则的启发式求解方法, 在机器总成本不超过给定阈值的约束下, 使最大完工时间最小化. 针对流水作业车间调度问题, Ding等^[16]提出了一种多目标NEH算法和一种改进的多目标迭代贪心算法来解决置换流车间低碳调度问题, 旨在降低加工过程的能耗, 从而减少碳排放. Zhai等^[17]利用时间序列模型对部分可再生能源的电价进行逐时更新, 将电价反馈到调度模型中, 优化能源成本. Huang等^[18]通过优化维修流程, 提高了能源效率, 减少了两阶段多处理器流水车间调度问题中的最大完工时间. Lu等^[19]提出了一种混合多目标回溯搜索算法来提高置换流车间调度问题的能源效率, 该算法主要考虑了准备阶段和加工阶段的能源消耗.

综上所述, 近些年随着人们对环境的重视, 绿色调度的研究越来越多, 而在TFT-LCD制造cell阶段调度问题上, 大多数研究只考虑了经济效益, 并未考虑对环境的影响. 因此本文研究以最大完工时间和碳排放量为目标的TFT-LCD制造cell阶段绿色调度问题, 在考虑机器选择和工序的基础上, 增加了机器转速的选择, 不同的机器转速会影响加工时间的长短和碳排放量的多少. 本文提出一种改进布谷鸟搜索算法, 通过在步长因子加入动态系数, 提高算法的搜索效率和解的质量, 并构建Pareto最优解集.

1 问题描述 1.1 TFT-LCD装配过程描述

薄膜晶体管液晶显示器(TFT-LCD)的制造工艺由阵列工艺(array)、面板工艺(cell)和模块工艺(module)等3个基本工艺阶段组成. 除了材料成分外, TFT的阵列工艺与半导体晶圆的阵列工艺非常相似. 阵列工艺的主要原料是玻璃基板, 经过清洗、涂布、曝光、显影、蚀刻等5–7次加工. 面板工艺包括许多组装步骤来组装TFT玻璃基板和彩色滤光膜. 模块工艺是TFT-LCD制造工艺的最后一个阶段, 通过面板工艺生产的TFT-LCD面板与所有其他必要部件组装在一起, 完成最终的TFT-LCD产品.

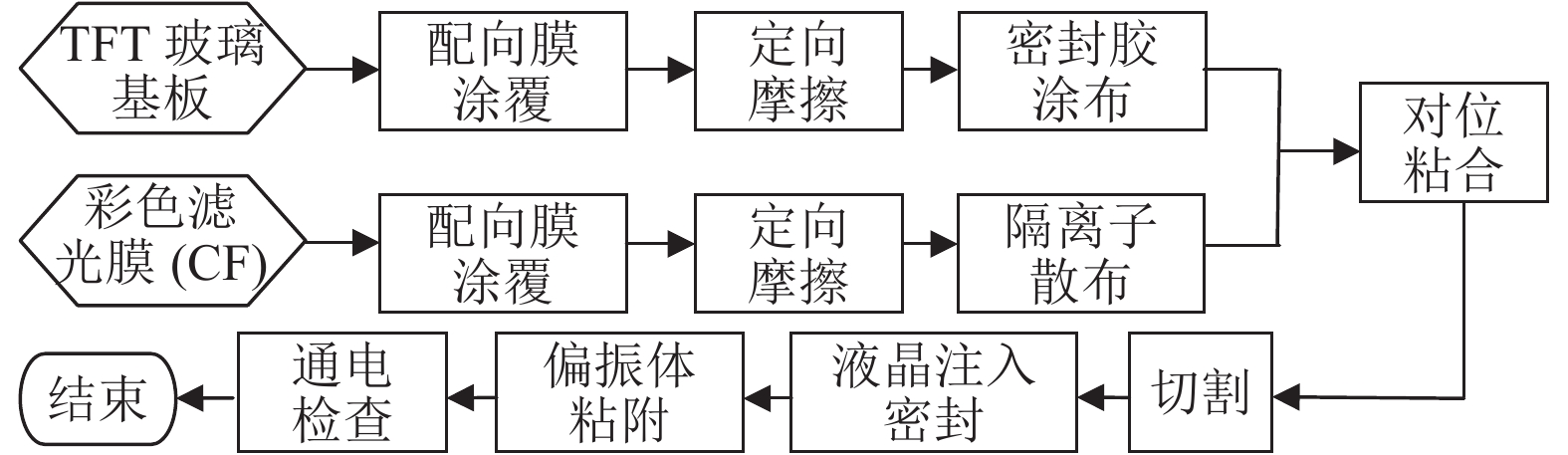
TFT- LCD制造中的cell阶段是将彩色滤光膜(CF)和TFT玻璃基板两个部件组装在一起的组装过程. 通常彩色滤光膜是从外部供应商购买的, 而TFT玻璃基板是由自己的阵列工厂生产的. 在整个组装过程中, TFT玻璃基板和彩色滤光膜分别经过配向膜印刷, 摩擦, 密封胶/隔离子涂布, 粘接, 切割, 填充液晶, 偏振片粘附和检查等11道工序. cell阶段可以看作非等效并行机的混合流水车间问题. cell阶段制造工艺流程如图1所示.

1.2 TFT-LCD制造cell阶段绿色调度模型建立

本文涉及的数学符号及含义如下:

${{n}}$ : 工件类型数( ${{i}} = 1,2, \cdots ,{{n}}$ );

${{N}}$ : 工件批数, 包括零件A, B及装配后工件C;

${{{J}}_{{r}}}$ / ${{{J}}_{{{{r}}^{\rm{*}}}}}$ : 第 ${{r}}$ /第 ${{{r}}^{\rm{*}}}$ 批零件或工件( ${{r}} = 1,2, \cdots ,{{N}}$ ), 其中, ${{r}}$ 代表零件A, ${{{r}}^{\rm{*}}}$ 代表零件B;

O_j: 工件第j道工序( ${{j}} \!=\! 1,2, \cdots ,{{a}},{{a}} \!+\! 1, \cdots ,{{b}},{{b}} \!+\! 1, \cdots ,$ ${{c}} $ ), 其中零件A批加工工序为 ${{j}} = 1,2, \cdots ,{{a}}$ , 零件B批加工工序为 ${{j}} = {{a}} + 1, \cdots ,{{b}}$ , 装配后工序为 ${{j}} = {{b}} + 1, \cdots ,{{c}}$ ;

m: 当前工序下的第m台机器( ${{m}} = 1,2, \cdots ,{{M}}$ );

${{{v}}_{\rm{l}}}$ : 每台机器的转速( ${{V}} = {{{v}}_1},{{{v}}_2}, \cdots ,{{{v}}_{{l}}}, \cdots ,{{{v}}_{{d}}}$ ), 共 ${\rm{d}}$ 种转速;

t_rjm: 第r批工件第j道工序在第m台机器上的开始加工时间;

P_rjm: 第r批工件第j道工序在第m台机器上的基础加工时间;

P_rjml: 第r批工件第j道工序在第m台机器上以转速l加工的时间;

D_rjm: 第r批工件第j道工序在第m台机器上的结束加工时间;

W_jml: 第j道工序第m台机器上以转速l加工的单位能耗;

l_jm: 第j道工序第m台机器上的单位空载能耗;

S_ij: 工序O_j不同类型工件之间转换的准备时间;

X_rjml: 第r批工件第j道工序在第m台机器以转速l加工为1, 否则为0;

Y_jrr'm: 在第j道工序, J_r先于J_r'在第m台机器上加工为1, 否则为0.

基于机器转速的cell阶段绿色调度在满足约束条件的前提下, 不仅要考虑机器的选择和工件的排序, 也要考虑机器转速的选择. 即在约束条件下对每一批工件, 确定加工工序, 选择合适的机器和转速, 确保最终优化目标达到满意解. 模型中涉及的假设如下:

(1)某一时刻, 每台机器只能加工一批工件(在装配工序中, 零件A和零件B合成一批工件C), 并且加工开始后, 机器转速保持不变.

(2)某一时刻, 一批工件只能在一台机器上加工, 并且加工开始后, 加工过程不能被中断.

(3)所有机器在整个调度期间都是可用的(没有机器故障).

(4)零件A、零件B和装配后工件C的加工路径事先确定.

(5)每道工序的加工时间由机器转速和工件类型共同决定.

因此, 本文建立基于机器转速的TFT-LCD制造cell阶段绿色调度模型, 优化目标为最大完工时间 ${{{T}}_{{\rm{max}}}}$ 和总碳排放量 ${{{C}}_{{\rm{total}}}}$ .

目标函数:

${{{T}}_{{\rm{max}}}} = \max \left( {{{{t}}_{{{rjm}}}} + {{{P}}_{{{rjml}}}}{{{X}}_{{{rjml}}}}} \right)$

(1)

$\begin{aligned} {C_{\rm{total}}} = &{\varepsilon \mathop \sum \limits_{j = 1}^{O_j} \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{r = 1}^{N} \mathop \sum \limits_{l = 1}^{d}} {\left( {{P_{rjml}}{X_{rjml}}{W_{jml}}} \right.}\\ &+{\left. {\left( {{D_{jm}} - {X_{rjml}}{P_{rjml}} - {t_{jm}}} \right){l_{jm}}} \right) } \\ \end{aligned} $

(2)

约束条件:

$\mathop \sum \limits_{j = 1}^{O_j} \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{l = 1}^{d} {X_{rjml}} \le 1$

(3)

$\mathop \sum \limits_{r = 1}^{N} {X_{rjml}} \le 1$

(4)

${{{Z}}_1}{{{X}}_{{{rjml}}}} \ge {{{t}}_{{{rjm}}}}$

(5)

${{{t}}_{{{rj'm'}}}} \ge {{{t}}_{{{rjm}}}} + {{{P}}_{{{rjml}}}}{{{X}}_{{{rjml}}}}$

(6)

${T_{{\rm{max}}}} = {t_{rjm}} + {P_{rjml}}{X_{rjml}}$

(7)

${t_{rjm}} + {P_{rjml}}{X_{rjml}} + {S_{ij}} - {t_{r'jm}} + {Z_2}\left( {{Y_{jrr'm}} - 1} \right) \le 0$

(8)

$\left( {{{{Y}}_{{{jrr'm}}}} + {{{Y}}_{{{jr'rm}}}}} \right) + {{{Z}}_2}\left( {{{{X}}_{{{rjml}}}} + {{{X}}_{{{r'jml}}}} - 2} \right) \le 1$

(9)

$\left( {{{{Y}}_{{{jrr'm}}}} + {{{Y}}_{{{jr'rm}}}}} \right) - {{{Z}}_2}\left( {{{{X}}_{{{rjml}}}} + {{{X}}_{{{r'jml}}}}} \right) \le 0$

(10)

$\left( {{{{Y}}_{{{jrr'm}}}} + {{{Y}}_{{{jr'rm}}}}} \right) - {{{Z}}_2}\left( {{{{X}}_{{{rjml}}}} - {{{X}}_{{{r'jml}}}} + 1} \right) \le 0$

(11)

${{{X}}_{{{rjml}}}} = {{{X}}_{{{{r}}^{{*}}}{{jml}}}}\left( {{{j}} = {{b}} + 1} \right)$

(12)

${{{t}}_{{{rjm}}}} = {{{t}}_{{{{r}}^{{*}}}{{jm}}}}\left( {{{j}} = {{b}} + 1} \right)$

(13)

式中, ${{{Z}}_1}$ 和 ${{{Z}}_2}$ 为足够大的正数. 式(1)中, ${{{T}}_{{\rm{max}}}}$ 代表最大完工时间; 式(2)中, ${{{C}}_{{\rm{total}}}}$ 代表碳排放总量, ${{\varepsilon }}$ 为能耗与碳排放量之间的转换系数, 通常取0.7559^[20]; 式(3)表示在某一时刻, 一批工件只能在一台机器上加工; 式(4)表示在某一时刻, 一台机器只能加工一批工件; 式(5)表示任何一批工件在某一机器加工时, 都有相应开始加工时间; 式(6)表示在加工过程中, 工件要严格按照事先确定的加工路径进行加工; 式(7)表示任何一批工件的结束加工时间不能超过最大完工时间; 式(8)表示同一台机器前后两批工件的开始加工时间约束; 式(9)~式(11)表示同一台机器加工不同工件批之间关系约束; 式(12)、式(13)表示装配工序时, 零件A和零件B同时在同一机器上加工.

2 改进布谷鸟搜索算法 2.1 标准布谷鸟搜索算法描述 2.1.1 布谷鸟繁殖行为

由于布谷鸟的寄生特性, 布谷鸟依赖于一些宿主种类并在宿主巢中下蛋. 宿主鸟会把布谷鸟的蛋误认成自己的蛋, 孵出布谷鸟的幼鸟. 然而, 并不是所有的布谷鸟蛋都不会被宿主鸟发现, 一旦发现, 宿主鸟会扔掉布谷鸟蛋或选择别处重新筑巢. 因此, 布谷鸟会选择一些与自身孵化方式相似的宿主鸟.

2.1.2 莱维飞行

除了布谷鸟的寄生特征外, Yang等^[21]提出的布谷鸟搜索算法(Cuckoo Search Algorithm, CSA)依赖于布谷鸟的觅食性质. 布谷鸟的觅食模式受到一个重要因素的控制, 这个因素被称为莱维飞行, 莱维飞行是了一种步长遵循重尾概率分布的结构化随机游走. 很多动物和昆虫的觅食路径也遵循以莱维飞行为特征的重尾概率分布的结构化随机游走^[22]. Yang等^[23]证明了用基于莱维飞行的结构化随机游走代替纯随机游走的布谷鸟搜索算法比许多现有的元启发式算法(如粒子群算法、蜂群算法和差分进化算法)更有效.

2.1.3 布谷鸟搜索过程

在布谷鸟搜索算法中, 巢中的蛋是一种解决方案, 布谷鸟蛋代表一种新的解决方案. 为新一代选择的鸟蛋质量较好的鸟巢, 对应的是鸟蛋产生新布谷鸟的能力. 布谷鸟搜索算法是基于以下假设构建的:

(1)每只布谷鸟选择一个宿主巢, 然后随机下蛋.

(2)为下一代选择最好的鸟巢.

(3)巢的数量保持不变, 宿主鸟可以以一定的概率 ${{pa}} \in \left[ {0,1} \right]$ 扔掉外来的蛋.

利用莱维飞行的布谷鸟第w个鸟巢第p+1代的位置为:

${{X}}_{{w}}^{{{p}} + 1} = {{X}}_{{w}}^{{p}} + {{\alpha Levy}}\left( \lambda \right)$

(14)

式(14)中, ${{X}}_{{w}}^{{p}}$ 是当前解, ${\rm{\alpha }} > 0$ 表示步长因子, 大小取决于问题的规模. 该值是常量, 它具有固定的、有限的时间复杂度. 布谷鸟随机选择宿主巢下蛋, 采用基于莱维飞行的随机游走. 莱维飞行符合以下概率分布:

${{Levy}}\left( \lambda \right) \sim {{u}} = {{{p}}^{ - \lambda }} \in \left( {1,3} \right]$

(15)

上述莱维分布服从重尾概率分布的阶跃幂律. 方差和均值都是无穷大. 步长将搜索域划分为局部搜索空间和全局搜索空间, 为全局搜索提供了机会, 而不是停留在局部最小值上. 由于布谷鸟搜索算法采用的是在莱维飞行中进行全局随机游走, 因此能够更快的在搜索空间内达到最优.

2.2 改进布谷鸟搜索算法描述

在标准布谷鸟搜索算法中, 步长因子为固定的值. 步长因子的大小会直接影响求解的速度和效率, 当步长因子过大时, 虽具备较好的全局搜索能力, 收敛速度也快, 但易错过全局最优解或在全局最优解附近震荡; 当步长因子过小时, 收敛速度变慢, 也易陷入局部最优解中, 该缺点限制了CSA算法的快速收敛性, 并有可能导致无法获得高质量的解. 因此, 为了更好实现全局快速搜索和局部精确搜索, 朝着全局最优解快速而稳定的搜索, 本文提出一种改进布谷鸟搜索算法(Improved Cuckoo Search Algorithm, ICSA), 在步长因子 ${{\alpha }}$ 前加入动态系数 ${\rm{\beta }}$ , 如式(16):

${{\beta }} = {{\omega }}\left( {{{T}}\_{max} - {{Times}}} \right) + {{{\beta }}_0}$

(16)

式(16)中, ${{T}}\_{{max}}$ 表示最大迭代次数, ${{Times}}$ 表示当前迭代次数, ${\rm{\omega }} > 0$ 表示变化率, 控制减小的幅度, ${{\rm{\beta }}_0} > 0$ 表示最小动态系数, 防止步长因子缩减到0, ${\rm{\omega }}$ 和 ${{\rm{\beta }}_0}$ 的大小取决于问题的规模. 可以看出, 动态系数 ${\rm{\beta }}$ 随着迭代次数的增加而线性递减, 一方面, 在搜索前期, 有利于对全局进行快速搜索, 寻找优质解所在区域; 在搜索后期, 有利于加深对优质解周边区域精确搜索, 找到优质解; 另一方面, 动态系数能够有效的提高算法的搜索能力, 平衡全局搜索和局部搜索的关系, 通过迭代前期较大的动态系数, 扩大搜索空间, 加强全局搜索的能力, 迭代后期较小的动态系数, 使得算法的局部搜索能力不断加强. 因此, 改进布谷鸟搜索算法的更新位置公式为式(17):

${{X}}_{{w}}^{{{p}} + 1} = {{X}}_{{w}}^{{p}} + {{\beta \alpha Levy}}\left( \lambda \right)$

(17)

相比于其他改进方式, 本文提出的改进方式参数少, 实现方式简单, 求解速度快.

2.3 构建Pareto最优解集

与单目标优化问题不同的是, 多目标优化问题目标之间可能存在矛盾, 这时可以构建Pareto最优解集来解决. Pareto最优解集是指: 在解集K中, 对于解x、y, 若解x的所有目标函数值不劣于解y, 且解x至少存在一个目标函数值优于解y, 则称x支配y, 记作 ${{x}} \prec {{y}}$ , 若解集K中不存在任一解的所有目标函数值不劣于解x, 且存在一个目标函数值优于解x, 则称解x为Pareto最优解集中的一个解.

本文结合双元锦标赛和动态淘汰制2种方法构建Pareto最优解集. 实现过程为: 选择解集K中的一个解x, 将其与剩余解进行比较, 若存在解被x支配, 则把该解从解集K中删除, 若存在解支配x, 则直接把解x从解集K中删除, 若剩余解皆不支配x, 则把解x加入Pareto最优解集中, 并把解x从解集K中删除, 重复这一步骤, 直至解集K为空集. 若存在上代Pareto最优解集, 合并两代Pareto最优解集, 继续比较. 若Pareto最优解集规模大于规定值, 则使用聚焦距离进行筛选.

2.4 改进布谷鸟搜索算法步骤描述

改进布谷鸟搜索算法遵循以莱维飞行为特征的重尾概率分布的结构化随机游走. 莱维飞行为全局搜索提供了机会, 而改进布谷鸟搜索算法在搜索前期, 有利于对全局进行快速搜索, 寻找优质解所在区域; 在搜索后期, 有利于加深对优质解周边区域精确搜索, 找到优质解. 在结合双元锦标赛、动态淘汰制和聚焦距离筛选3种方法之后, 改进布谷鸟搜索算法步骤如下:

(1)参数初始化. 设置种群规模: z; 最大迭代次数: ${{T}}\_{{max}}$ ; 被宿主发现的概率: pa; Pareto解的个数: Z; 步长因子: ${{\alpha }}$ ; 变化率: ${{\omega }}$ ; 最小动态系数: ${{{\beta }}_0}$ .

(2)种群初始化. 随机选取z个鸟巢位置.

(3)计算鸟巢位置所对应的两个目标函数值, 构建初始Pareto最优解集.

(4)根据式(17)得到下一代鸟巢位置, 并计算其目标函数值.

(5)每个新鸟巢随机产生一个R, 如果R大于被宿主发现的概率pa, 返回步骤(4), 否则, 进入步骤(6).

(6)比较两代鸟巢目标函数值, 构建新Pareto最优解集, 如果Pareto最优解个数大于Z, 那么使用聚焦距离进行筛选.

(7)若达到最大迭代次数 ${{T}}\_{{max}}$ , 输出最终Pareto最优解集, 否则, 回到步骤(4).

3 实验与结果分析 3.1 TFT-LCD制造cell阶段问题编码

TFT-LCD制造cell阶段绿色调度需要同时考虑当前工件工序机器选择、机器转速选择和工件在机器上加工顺序, 为此, 本文设计一种基于机器选择、转速选择和工序选择相结合的三段式编码方式, 如图2所示.

图2中, 在基于机器编码中, 下行数字表示工件编号, 上行数字表示当前工件加工机器编号, 表示的机器依次是{ ${{{m}}_3},{{{m}}_5},{{{m}}_1},{{{m}}_4},{{{m}}_2},{{{m}}_3},{{{m}}_4},{{{m}}_1}$ }; 在基于转速编码中, 下行数字表示机器标号, 上行数字表示当前机器转速编号, 表示的转速依次是{ ${{{v}}_3},{{{v}}_2},{{{v}}_5},{{{v}}_3},{{{v}}_5},{{{v}}_1},{{{v}}_4},$ ${{\rm{v}}_2} $ }; 在基于工序编码中, 数字表示工件编号, 出现频次表示当前工序数, 表示的工序依次是{ ${{{O}}_{21}},{{{O}}_{31}},{{{O}}_{11}},{{{O}}_{41}},{{{O}}_{12}},$ ${{{O}}_{32}},{{{O}}_{22}},{{{O}}_{42}} $ }. 第一段编码确定当前工件工序的加工机器, 第二段编码确定当前加工机器的转速, 第三段编码确定工件工序的加工顺序, 三段编码相结合确保所求解可行.

3.2 测试实例和对比算法

Ding等^[16]提出了一种关于加工时间和能耗之间的假设: 对于确定的工序和机器, 随着转速的变大, 加工时间减少, 能耗增加, 即对于 $\forall {{{v}}_{{l}}} > {{{v}}_{{g}}},{{l}},{{g}} \in \left\{ {1,2, \cdots ,{{d}}} \right\}$ 满足 ${{{P}}_{{{rjml}}}} < {{{P}}_{{{rjmg}}}},{{{P}}_{{{rjml}}}} \times {{{W}}_{{{jml}}}} > {{{P}}_{{{rjmg}}}} \times {{{W}}_{{{jmg}}}}$ . 测试实例选取某车间的实际生产数据^[8], 产品类型及批量数如表1所示, 工序机器数如表2所示, 不同工件工序在机器上的加工时间如表3所示, 不同类型工件在各工序之间转换的准备时间如表4所示. 需要增加机器转速和能耗信息, $ {{v}} = \left\{ {1.00,1.30,1.55,1.80,2.00} \right\} $ , ${{{W}}_{{{jml}}}} = 4 \times {{v}}_{{l}}^2$ , $ {{{l}}_{{{jm}}}} =$ 1, 显然加工时间和能耗之间的关系满足上述假设.

本文选择标准布谷鸟搜索算法(CSA)和Deb等^[24]提出的带精英策略的快速非支配排序遗传算法(NSGA-II)作为对比算法. 由于原算法没有对机器转速选择进行编码, 对于CSA, 采取与本文一致的编码方式; 对于NSGA-II, 增加机器转速的选择、交叉和变异部分. 两种算法构建Pareto最优解集的方法与本文一致.

3.3 结果分析

求解cell阶段绿色调度问题算法的运行环境为: 操作系统为Windows 10, 处理器为Intel(R) Core(TM) i5-3210M, 主频为2.50 GHz, 内存为6 GB, 编程环境为Matlab R2018a.

基于大量测试得到, 当变化率 ${\rm{\omega }}$ 为0.02, 最小动态系数 ${{\rm{\beta }}_0}$ 为0.5时, 算法性能最佳, 因此ICSA的6个参数, 设计如下: 种群规模z为50, 最大迭代次数 ${{T}}\_{{max}}$ 为100, 被宿主发现的概率pa为0.25, 步长因子 ${\rm{\alpha }}$ 为0.1, 变化率 ${\rm{\omega }}$ 为0.02, 最小动态系数 ${{\rm{\beta }}_0}$ 为0.5; CSA具有4个参数, 设计如下: 种群规模z为50, 最大迭代次数 ${{T}}\_{{max}}$ 为100, 被宿主发现的概率pa为0.25, 步长因子 ${\rm{\alpha }}$ 为0.1; NSGA-II具有5个参数, 设计如下: 种群规模为50, 最大迭代次数为100, 选择概率为0.9, 交叉率为0.8, 变异率为0.1. 3种算法Pareto解的个数Z都为10.

每种算法各运行30次, 每次运行结果的最好解(取整)如表5所示.

一方面, 总共30次运行结果中, ICSA在23次运行中得到了优于CSA和NSGA-II的最好解, 剩余7次运行结果也只是单个目标值劣于CSA或NSGA-II, 没有两个目标值都劣于CSA或NSGA-II的情况发生. 另一方面, 表5中有4次最大完工时间小于450, 3次碳排放总量小于10 000, 均由ICSA运行得到, 说明ICSA能够得到更好的解.

图3是独立运行一次, 不同算法求得的Pareto解分布对比图. 图中, 叉号、五角、圆圈分别代表ICSA、CSA、NSGA-II求得的解. 可以看出, ICSA所求解最好, CSA次之、NSGA-II最差. ICSA的10个解支配CSA的8个解和NSGA-II的10个解, 即在最大完工时间相同的情况下, 碳排放总量更小. 因此, ICSA的表现要优于CSA和NSGA-II. 另外, 最大完工时间越短, 碳排放量越高, 因此在完工时间允许的情况下, 选择较低的转速, 可以有效的减少碳排放量.

综上所述, 结合表5和图3可以得到, 在求解基于机器转速的TFT-LCD制造cell阶段绿色调度问题上, ICSA的求解质量要高于CSA和NSGA-II.

4 结论与展望

本文研究基于改进布谷鸟搜索算法的TFT-LCD制造cell阶段绿色调度问题, 建立以最小化最大完工时间和碳排放总量为目标的数学模型. 对基于机器选择、转速选择和工序选择相结合的三段式编码后, 应用一种改进布谷鸟搜索算法进行求解, 该算法在步长因子前加入动态系数, 使其在搜索前期, 快速对全局进行搜索, 在搜索后期, 加深对局部进行搜索, 提高了解的质量. 并对某车间的实际生产数据进行仿真, 实验结果表明, 相比于CSA和NSGA-II, 在最大完工时间相同的情况下, ICSA可以有效的减少碳排放量. 关于TFT-LCD多目标绿色调度的研究才刚刚开始, 作者会继续研究关于TFT-LCD制造array阶段和module阶段绿色调度问题, 同时作者将深入研究ICSA和其他智能算法及改进策略, 为后续研究的问题提供算法支撑.