极限学习机由于其快速的训练速度, 良好的泛化能力, 广泛应用于各行业研究中, 例如面部识别、图像分割和人类动作识别^[1]. 在实际应用中, 为了达到理想的预测效果, 需要选取预测精度较高的机器学习方法. 极限学习机的预测精度受到隐藏层节点数目、隐藏层的任意生成的输入参数和数据噪声的影响. 这种不更新隐藏层参数, 通过最小二乘调整的输出权重使极限学习机的抗错能力较差, 容易夸大离群点和噪声的影响得到不准确的结果. 在一些应用中, 针对极限学习机隐藏层节点过多的缺陷, 在隐藏层中增加了一类分类神经元^[2]. 或者通过粒子群算法优化选择极限学习机的隐藏层偏置, 验证了粒子群极限学习机算法在隐含层节点数目选择上具有优势^[3].

现实生活中存在许多与机器学习方法的应用条件不一致的情况, 因此对大多数传统算法进行改进以适应当前情况是正常的. 王莉等^[4]在代价敏感的理论基础上, 提出一种新的基于代价敏感集成学习的非平衡数据分类方法. 郑仙花等^[5]通过进化学习改进了克隆选择算法实现了多类监督分类, 避免了只能针对某一类样本数据进行监督学习. 沈宋衍等^[6]基于在线回归学习提出一种轮廓跟踪算法, 解决了目标快速运动以及严重形变导致跟踪失败的问题. 王英博等^[7]提出采用修正型果蝇优化算法优化广义回归神经网络进行参数优化. 蒙凯等^[8]基于集成问题的离散特征, 提出面向多目标优化的改进灰狼算法. 赵燕伟等^[9]以关联函数为基础, 重新定义神经网络中的误差计算方法, 构建了一种基于改进BP神经网络的可拓分类器.

由于极限学习机的学习效果依赖于初始的隐藏层输入权值和偏置. 本研究认为极限学习机可以利用模拟退火算法不断尝试隐藏层输入权值和偏置的选择, 提升预测能力. 首先, 传统的极限学习机对训练集的学习过程, 可以得到一组隐藏层的输入权值、偏置、输出权值和均方根误差. 然后把得到的隐藏层输入权值和偏置作为初始解, 均方根误差视为目标函数, 通过模拟退火过程, 找到训练过程均方根误差最小的极限学习机的隐藏层输入权值和偏置, 再通过传统的极限学习机计算得到隐藏层输出权值. 最后文本为了测试改进后的极限学习机的预测能力, 选取了鸢尾花分类数据和波士顿房价预测数据分别进行了分类和回归实验, 实验结果表明基于模拟退火改进的极限学习机在分类和回归的预测能力上优于传统的极限学习机.

1 基于SA改进的ELM预测模型 1.1 极限学习机

极限学习机作为单隐层神经网络, 与传统的神经网络相比, 优势在于收敛速度快、泛化能力强, 并且避免了反向传播神经网络易陷入局部最优, 由于迭代, 训练过程十分耗时等特点^[10]. 极限学习机任意初始化输入权重和偏置, 通过计算隐藏层神经元的输出权值, 加快了极限学习机的学习速度. 根据线性方程组的求解方法可知, 当样本隐藏层神经元输出值矩阵是满秩时, 只需要矩阵求逆这一次性的操作, 就可以得到隐藏层神经元权重. 这一过程恰好可以学习不同的观测样本. 极限学习机的学习算法如下所示:

对于 ${{N}}$ 个随机样本 $\left( {{x_i},{y_i}} \right)$ , 其中 $ {x_i} = [{x_{i1}},{x_{i2}}, \cdots ,$ ${{{x}}_{in}}]^{\rm{T}} \in {R^n}$ . 一个具有L个隐藏层神经元, 激活函数为 ${{g}}(x)$ 的极限学习机可以表示为 $\displaystyle \sum\limits_{j = 1}^L {{\beta _j}} g\left( {{W_j}*{x_i} + {b_j}} \right) = {o_i}$ , $i = 1, \cdots ,N $ , ${W_j} = {[{w_{j1}},{w_{j2}}, \cdots ,{w_{jn}}]^{\rm{T}}} \in {R^n}$ , ${\beta _j}$ 为输出权重, ${{b}_j}$ 是第 ${j}$ 个隐藏层神经元的偏置, ${W_{j}}{*}{x_i}\;$ 表示 ${W_j}$ 和 ${x_i}$ 的内积. 极限学习机训练样本的目的是使输出的误差小, 即 $\displaystyle \sum\limits_{i = 1}^N {||{o_i} - {{{y}}_i}||} = 0$ , 也就是存在 $\;{\beta _j}$ , ${W_j}$ 和 ${b_j}$ , 使 $\displaystyle \sum\limits_{{{j = 1}}}^L {{\beta _j}} g({W_j}{{*}}{x_i} + {b_j}) = {y_i}$ , $i = {{1}}, \cdots ,{{N}}$ , 矩阵形式表示为: $H\beta = Y$ , 其中H是隐藏层神经元输出, $\;\beta $ 是输出权重, $Y$ 为样本观测值.

$ \begin{array}{l} H({W_1}, \cdots ,{W_L},{b_1}, \cdots ,{b_L},{x_1}, \cdots ,{x_N})\\ {\rm{ = }}{\left[ \begin{array}{ccc} g({W_1}*{x_1} + {b_1}) & \cdots & g({W_L}*{x_1} + {b_L})\\ \vdots & \ddots &\vdots\\ g({W_1}*{x_N} + {b_1}) & \cdots& g({W_L}*{x_N} + {b_L}) \end{array} \right]_{N \times L}} \end{array} $

$ \beta = {\left[ \begin{array}{l} \beta _1^{\rm{T}}\\ \; \vdots \\ \beta _L^{\rm{T}} \end{array} \right]_{L \times m}},Y = {\left[ \begin{array}{l} {{y}}_1^{\rm{T}}\\ \; \vdots \\ y_N^{\rm{T}} \end{array} \right]_{N \times m}} $

通过解方程得到 $\;\hat \beta $ , $\;\hat \beta = {H^+ }Y$ , H⁺是矩阵H的Moore-penrose广义逆. 为解决隐藏层输入权值和偏置的任意性, 周华平等^[11]结合改进鱼群算法对极限学习机的隐藏层偏置进行优化, 提出了乳腺肿瘤诊断的方法. 赵建堂^[12]采用有序加权平均算子融合单一极限学习的输出信息, 使分割式极限学习机的输出结果更为稳定.

1.2 模拟退火算法

模拟退火算法作为一种迭代自适应启发式概率性搜索算法, 模拟了一个高温固体的退火过程, 将优化过程分成加温、等温、冷却等3个部分, 利用Metropolis算法适当的控制温度下降过程. Metropolis准则是模拟退火算法收敛于全局最优解的关键所在, 它以一定的概率接受恶化解, 这就使算法跳离局部最优的陷阱^[13]. 具体来说, 模拟退火算法通过迭代的方式尝试改进目标函数的最优解, 改进的新解将被接受为最优解, 当新解劣于当前最优解, 由波尔茨曼概率确定一个劣解的概率, 使目标函数避免局部最优, 最终获得全局最优解^[14]. 模拟退火算法的具体实现步骤算法1所示.

算法1. 模拟退火算法

1)初始化, 取足够大的初始温度 $\scriptstyle {T_0}$ , 令 $\scriptstyle T = {T_0}$ , 任意选取初始解 $\scriptstyle{S_1}$ , 确定每个温度下的迭代次数L和结束温度 $\scriptstyle{{T}_{{\rm{end}}}}$ .

2)对当前温度T和 $\scriptstyle{k} = {{1,2,}} \cdots {{,L}}$ , 重复第3)步至第5)步.

3)随机产生一个新解 $\scriptstyle{S_2}$ .

4)计算 $\scriptstyle \Delta {f} = {f}({S_2}) - f({S_1})$ , 其中 $\scriptstyle{f}({S_1})$ , $\scriptstyle{f}(S_2)$ 分别是 $\scriptstyle{S_1}$ , $\scriptstyle{S_2}$ 的代价函数.

5)若 $\scriptstyle\Delta {{f < }}0$ , 则接受 $\scriptstyle{S_2}$ 作为新的当前解, 令 $\scriptstyle{S_1} = S_2$ ; 否则计算 $\scriptstyle{S_2}$ 的接受概率 $\scriptstyle{\exp}( - \Delta f/T)$ , 若产生(0,1)区间的随机数rand, $\scriptstyle{{\exp}}( - \Delta f/T) > {\rm{rand}}$ , 也接受 $\scriptstyle{S_2}$ 作为新的当前解, $\scriptstyle{S_1} = {S_2}$ ;否则当前解 $\scriptstyle{S_1}$ 不变.

6)降温速度为 $\scriptstyle{q}$ , $\scriptstyle{T} = {q*T}$ , 若T小于 $\scriptstyle{T_{\rm{end}}}$ , 则停止迭代, 输出当前解, 否则继续迭代.

在应用中模拟退火算法发挥了重要的作用, 高鹰等^[15]提出一种基于模拟退火的粒子群优化算法, 改善了粒子群优化算法摆脱局部极值点的能力, 提高了算法的收敛速度和精度. 杨若黎等^[16]提出一种确定模拟退火算法温度更新函数的启发式准则, 数值计算结果表明采用新的温度更新函数以及相应的概率密度函数的模拟退火算法可以显著地提高求解全局优化问题的计算效率. 张世睿等^[17]提出一种基于模拟退火算法的单隐藏层BP神经网络隐藏层节点估算算法, 通过模拟退火不断增加隐藏层节点个数直至算法结束, 得到最优解. 凌静等^[18]用模拟退火算法改进遗传算法的变异操作, 改善了遗传算法的早熟现象. 黄联标等^[19]基于模拟退火算法对多工程系统维护时刻和维护方案进行寻优, 确定各个工段最佳的预防性维护策略.

1.3 改进的极限学习机

由于极限学习机是任意给定隐藏层神经元的权值和偏置, 这导致一些隐藏层神经元在训练过程中无效, 使得极限学习机的泛化能力降低. 由于ELM学习算法随机选择隐藏层神经元的输入权值和偏置, 但是这些输入权值和偏置相对与输入数据来说, 不是最优的选择, 这使得极限学习机的泛化能力降低. 在实际应用中, 为了使神经网络有较好的泛化能力, 需要较多的隐含层神经元, 因而增加了网络的复杂度. 罗庚合^[20]为了减少隐含层神经元个数、提高网络的泛化性能, 引入可拓聚类算法, 动态调整隐藏层节点数目. 针对以上问题本文提出基于模拟退火算法的极限学习机, 利用模拟退火算法选择极限学习机的输入权值和偏置, 从而得到一个最优的训练网络.

基于模拟退火算法改进的极限学习机算法算法2所示.

算法2. 基于模拟退火算法改进的极限学习机算法

1)任意生成输入权值 $\scriptstyle W_{L \times N}^0$ 和偏置 $\scriptstyle{b}_L^0$ , 极限学习机学习训练集, 得到输出权值 $\scriptstyle{\hat \beta ^0}$ , 均方根误差为预测评价标准, 计算训练误差 $\scriptstyle{rms}e^0$ .

2)设置初始温度 $\scriptstyle{T} = T_0$ , 结束温度 $\scriptstyle{T_{{\rm{end}}}}$ , 每个温度下的迭代次数L, 降温速度 $\scriptstyle{q}$ , 令 $\scriptstyle{k} = 0$ .

3)任意生成输入权值 $\scriptstyle{W_{L \times N}}$ 和偏置 $\scriptstyle{b_L}$ , 并且 $\scriptstyle{W_{L \times N}} \ne W_{L \times N}^0$ , $\scriptstyle{b_L} \ne {{b}}_L^0$ . 极限学习机学习训练集, 得到输出权值 $\scriptstyle \;\hat \beta $ . 设置代价函数即均方根误差 $\scriptstyle rmse$ , $\scriptstyle k = k +1$ .

4)若 $\scriptstyle \Delta f = rmse - rms{e^0},\;\Delta f< 0$ 成立, 则 $\scriptstyle W_{L \times N}^0 = {W_{L \times N}}$ , $\scriptstyle{b}_L^0 = {b_L}$ ; 若不成立, 则计算输入权值 $\scriptstyle{W_{L \times N}}$ 和偏置 $\scriptstyle{b_L}$ 的接受概率 $\scriptstyle{exp}( - \Delta {{f}}/T)$ , 并且生成一个(0, 1)区间的随机数rand, 若 $\scriptstyle{exp}( - \Delta {{f}}/T) > {\rm{rand}}$ 成立, 则 $\scriptstyle W_{L \times N}^0 = {W_{L \times N}}$ , $\scriptstyle{b}_L^0 = {b_L}$ ; 否则返回第3)步.

5)若 $\scriptstyle k > L$ 成立, 则 $\scriptstyle T = T*q$ , $\scriptstyle k = 0$ , 否则返回第3)步.

6)若 $\scriptstyle T = {T_{end}}$ 不成立, 则返回第3)步, 若成立, 则算法结束, 得到最优的输入权值 $\scriptstyle W_{L \times N}^0$ 和偏置 $\scriptstyle{b}_L^0 $ .

基于模拟退火算法改进的极限学习机, 结构复杂不便理论分析, 若要了解算法的收敛性, 可采用数值实验的方法. 计算该算法的目标值与问题已有最优值之比, 利用概率统计的方法考察所得比值与1的接近程度, 比值越接近于1, 说明算法性能越好^[21].

2 实验分析

为了说明基于模拟退火算法改进的极限学习机的收敛性和泛化效果, 文本选取了鸢尾花分类样本和波士顿房价预测两个数据集分别进行定性预测和定量预测两组实验. 将基于模拟退火算法改进的极限学习机的预测结果与极限学习机等其他方法的预测结果进行对比. 两组实验参数如表1所示.

2.1 鸢尾花分类

本研究采用的鸢尾花数据包含4个解释变量分别是萼片的长度、萼片的宽度、花瓣的长度、花瓣的宽度, 被解释变量即鸢尾花的种类. 在这150条数据中, 包含了3种鸢尾花, 分别为setosa、versicolor、virginica, 每种花各有50条数据. 实验按2:1的比例将数据随机地划分成训练数据集和测试数据集. 研究选取精度为衡量预测准确性的标准, 对实验结果进行分析, 精度计算公式如表2所示.

任意选取一次实验进行观测, 结果如图1所示, 基于模拟退火改进的极限学习机在降温的过程中, 分类预测误差得到优化, 未改进的极限学习机的预测精度是88%, 改进后的极限学习机的预测精度将近98%, 预测精度提高了10%.

实验对每种分类方法的50次分类精度取平均值, 再进行比较. 实验发现极限学习机的分类精度是6种方法里最低的, 只有83.2%, 不足90%, 其余的分类方法的预测精度都高于90%. 其中, 本文方法的预测精度最高, 达到99.0%, 可见本文方法可以极大的提高极限学习机的分类预测精度. 如表3所示

通过对50次实验结果取平均值, 由表4发现随着鸢尾花样本数据规模越大, 比值越接近1, 说明样本数据越大, 改进后的极限学习机分类性能越好.

2.2 波士顿房价预测

本研究选取的波士顿房价数据集共有506条数据, 每一条数据包括13个解释变量和1个被解释变量. 解释变量包括城镇人均犯罪率、住宅用地所占面积、城镇中非商业用地的所占面积、是否邻近查尔斯河、环保指标、每栋住宅的房间数、1940年以前建成的自住建筑的比例、距离波士顿就业中心的加权距离、距离高速公路的便利指数、每万美元的不动产税率、城镇中教师学生的比例、城镇中黑人比例、房东是低收入阶层的比例. 被解释变量即自住房屋房价的中位数. 实验按2:1的比例将数据随机地划分成训练数据集和测试数据集, 选择均方根误差为预测误差的评价标准, ${{rmse}} = \sqrt {\frac{1}{m}\displaystyle \sum\limits_{i = 1}^m {{{({y_i} - {{\hat y}_i})}^2}} } $ , 其中, $m$ 是预测样本数, ${y_i}$ 是实际值, ${\hat y_i}$ 是预测值.

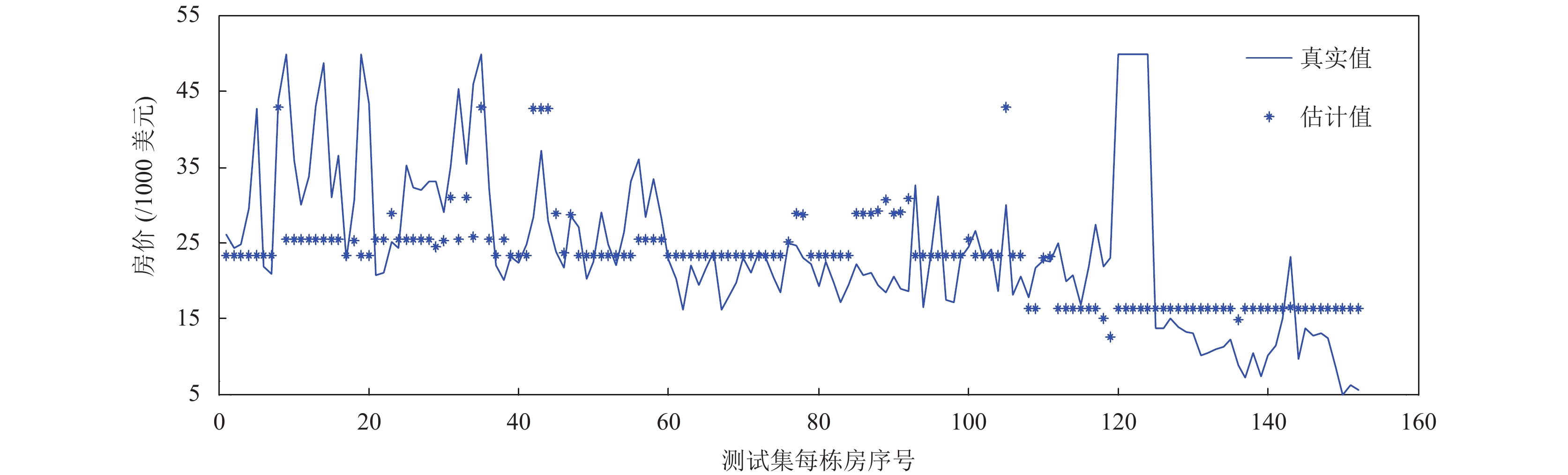
任意选取一次实验进行观测, 结果如图2~图4所示. 其中图2说明了未改进的极限学习机在测试集上的估计值和真实值的对比. 图3说明了改进后的极限学习机的在测试集上的估计值和真实值的对比.

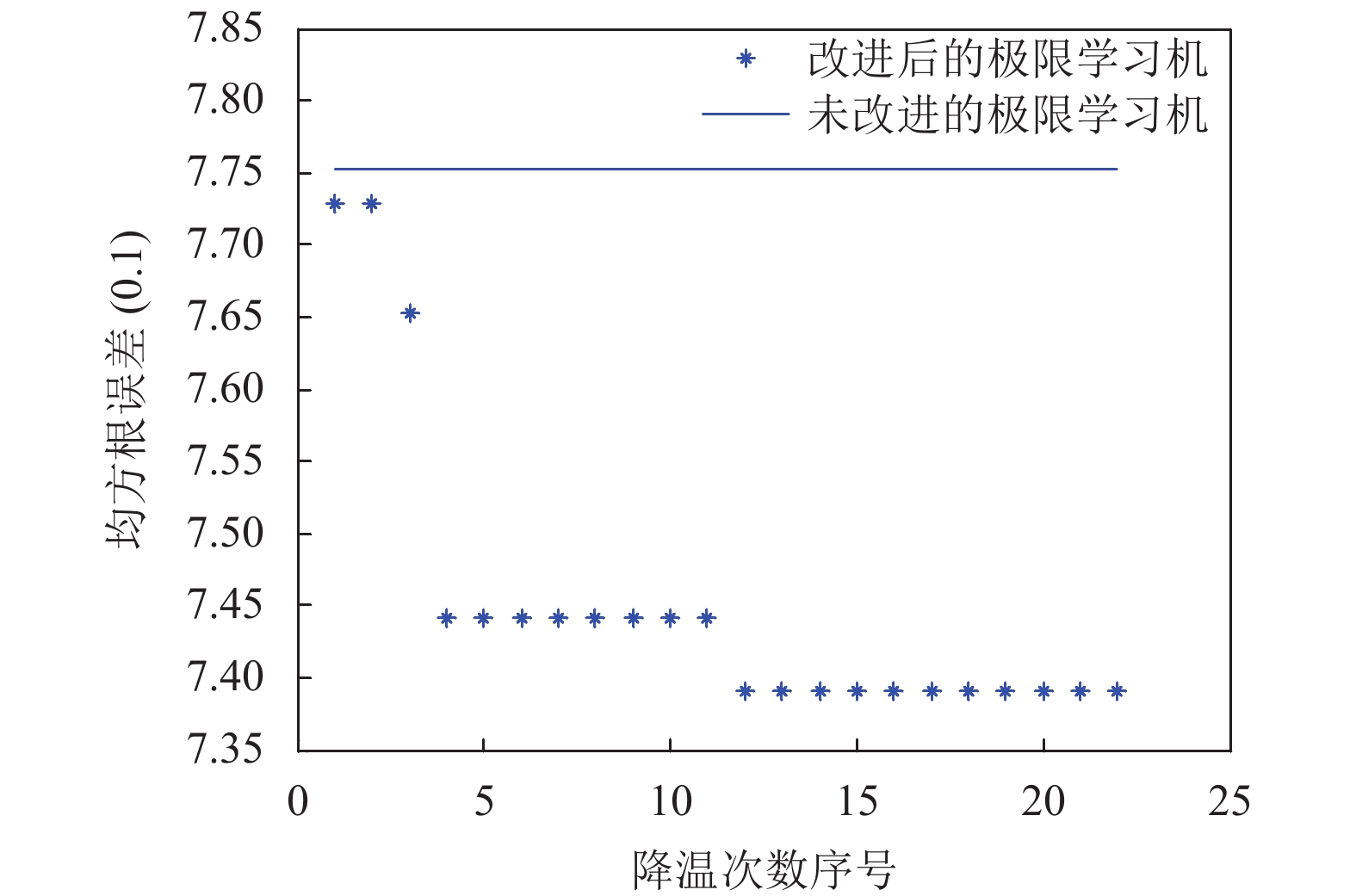
从图2中可知, 未改进的极限学习机在测试集上的一些预测值比实际值偏大. 从图3中可知, 改进后的极限学习机在测试集上的预测值相对平稳, 波动较为平缓. 图4表明基于模拟退火改进的极限学习机的优化过程, 均方根误差在优化过程中减小.

实验对每种分类方法的50次预测误差取平均值, 再进行比较, 实验结果如表5所示. 实验发现极限学习机的预测误差相比于其他传统机器学习方法偏高. 本文方法可以提高极限学习机的回归预测能力. 由表6发现波士顿房价样本数据规模越大, 比值在1附近有微小的变动, 说明改进后的极限学习机回归性能稳定.

3 结论与展望

为了提高极限学习机的分类和回归的预测能力, 提出一种基于模拟退火改进的极限学习机. 本文利用模拟退火算法的降温过程对隐藏层的输入权值和偏置进行优化, 避免了任意选择的输入权值和偏置使训练的模型无效的情况, 使极限学习机的表现更加稳定. 实验结果表明通过模拟退火算法改进的极限学习机分类预测能力极好, 回归预测能力劣于BP神经网络和回归树的预测能力.

下一步工作考虑改进的极限学习机在降温优化过程中如何选择最优的迭代次数、在优化时选择最优的隐藏层神经元个数以及如何进一步提高极限学习机的回归预测能力.