2. 广东省电信规划设计院有限公司, 广州 510630;
3. 华南理工大学, 广州 510641
2. Guangdong Planning and Designing Institute of Telecommunications Co. Ltd., Guangzhou 510630, China;
3. South China University of Technology, Guangzhou 510641, China
正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)是一种应用十分广泛的高速无线通信技术, 已经写入多个无线通信标准当中, 例如: WiFi、WiMax和LTE等. OFDM将宽带系统划分成多个相互正交的窄带子信道, 只需要在每个子信道上进行简单的单抽头均衡就可克服信道的频率选择性问题, 实现高谱效的通信. OFDM系统的对时间同步误差非常敏感, 必须为其设计可靠的同步方法[1]. 通常, OFDM系统中的定时方法分为两类: 盲方法和基于辅助数据的方法. 考虑到基于辅助数据方法在可靠性和计算复杂度方面都均优于盲同步算法, 本文研究基于辅助数据的定时同步算法.
在文献[2]中, Schmidl等提出了一种基于二段重复前导的定时和频率估计方法, 算法计算复杂度低且鲁棒性好. 然而, 其定时测度函数中存在一个平台, 使定时均方误差较大. 为了提高定时准确性, Minn等在文献[3]中通过将长度等于循环前缀的矩形与Schmidl的定时测度作卷积消除了测度函数中的平台. Shi等[4]扩展了Minn的方法并利用所有可能的自相关乘积项来获得更高的精度. 然而, 由于定时测度函数存在旁瓣, 文献[3]和[4]所提方法的估计精度仍然受限. 在文献[5]中, Park等提出了一种由两个对称部分组成的辅助数据前导, 通过对称自相关操作, 得到一个非常尖锐的定时测度. 文献[2–5]所提算法都是基于自相操作运算, 这些算法对接收机的载波偏移不敏感且实现简单.
在文献[6–8]中, 几种基于本地辅助数据与接收信号互相关操作的同步算法被提出, 这些算法的定时测度函数都具呈脉冲状. 文献[6,7]的方法容易受到载波频偏的影响. 文献[8]所提出的定时算法具备对抗微小频偏的能力, 但当频偏绝对值大于子载波间隔时, 算法不能稳健工作.
继自相关类算法与互相关类算法之后, 多个基于自相关和互相关相结合的算法被提出[9–11]. 文献[9]提出了一种伪噪声序列加权的辅助序列, 利用辅助序列特定结构设计定时算法, 显著提高了定时偏移估计的准确性. 在文献[10,11]中, Abdzadeh-Ziabari等和Liu等提出了一种与辅助数据结构无关的定时算法, 相关操作中所采用的乘积项数大大超过了其之前的算法, 使得定时精度大大增强. 值得说明的是, 文献[11]的算法与文献[10]中的算法基本思想相同, 定时精度也一样, 但前者计算复杂度更低.
为了进一步提高定时同步的性能, 本文研究基于最大似然 (Maximum-Likelihood, ML)准则的定时算法. 在文献[12–14]中, 已经提出了几种ML定时算法, 文献[12,13]中的ML估计器利用了辅助数据循环前缀中包含的冗余信息, 因而它们不适用于没有循环前缀的OFDM系统, 例如零前缀OFDM. 文献[14]中的ML估计器则依赖于具有多段重复结构的辅助数据. 与现有的ML定时算法不同, 本文研究独立于辅助数据结构的定时算法, 在无线通信工程中具有重要的应用价值.
1 信号模型在OFDM系统中, 发射机基带输出端的复值抽样信号可以表示为:
| $x(n) = \frac{1}{{\sqrt N }}\sum\limits_{k = 0}^{{N_{\rm{use}}} - 1} {{X_k}{e^{j2\pi kn/N}},{0} \le n \le N{\rm{ - }}1} $ | (1) |
其中,
| $\tilde x(n) = \left\{ {\begin{array}{*{20}{c}} {x(n + N), \; - G \le n \le - 1} \\ {x(n),\quad \quad 0 \le n \le N - 1} \end{array}} \right.$ | (2) |
其中, 循环前缀的长度应长于信道脉冲响应的可能长度.
参考文献[12,14]的做法, 本文在平坦衰落信道下推导ML定时算法. 所得算法在频率选择性信道下的性能将在算法仿真环节进行充分评估. 经过平坦衰落信道后的接收信号可以表示为:
| $r[n] = x[n - \tau ]{e^{j(2\pi \varepsilon n/N + \theta)}} + \omega [n]$ | (3) |
其中,
假设一个机基于帧传输的OFDM系统, 每个信号帧由辅助数据和M–1个OFDM符号组成. 辅助数据位于帧的起始处, 用向量表示为
不失一般性, 将接收到的与数据帧等长的抽样序列表示为:
| $\bar r = \{ r[n]|n = 0,1, \cdots ,\tau , \cdots ,MN - 1\} $ | (4) |
其中,
| $f(r(n)|\tau ,\varepsilon ,\theta)\! =\! \left\{ {\begin{aligned} & {\frac{1}{{\pi \sigma _\omega ^2}}\exp \left( - \frac{{{{\left| {r(n) \!- \!{s_{n - \tau }}{e^{j(2\pi \varepsilon n/N + \theta)}}} \right|}^2}}}{{\sigma _\omega ^2}}\right),n \!\in\! {{{I}}_p}} \\ & {\frac{1}{{\pi \sigma _1^2}}\exp \left( - \frac{{{{\left| {r(n)} \right|}^2}}}{{\sigma _1^2}}\right),n \in {{{I}}_d}} \end{aligned}} \right.$ | (5) |
显然,
| $f(\bar r|\tau ,\varepsilon ,\theta) = \prod\limits_{n \in {{\rm{I}}_p} \cup {{\rm{I}}_d}} {f(r(n)|\tau ,\varepsilon ,\theta)} $ | (6) |
因而,
| $\Lambda (\tau ,\varepsilon ,\theta) =\log\left( {f(\bar r|\tau ,\varepsilon ,\theta)} \right)$ | (7) |
通过将式(5)和式(6)代入式(7)中, 忽略其中的常数项(
| ${\Lambda ^{'}}(\tau ,\varepsilon ,\theta) = - {\rho _0}\sum\limits_{n \in {{\rm{I}}_d}} {{{\left| {r(n)} \right|}^2}} - \sum\limits_{n \in {{\rm{I}}_p}} {{{\left| {r(n) - {s_{n - \tau }}{e^{j(2\pi \varepsilon n/N + \theta)}}} \right|}^2}} $ | (8) |
其中,
| $\begin{aligned} \left( {{\tau _o},{\varepsilon _o},{\theta _o}} \right) & = \mathop {{\rm{argmax}}}\limits_{(\tau ,\varepsilon ,\theta)} - {\rho _0}\sum\limits_{n \in {{\rm{I}}_d}} {{{\left| {r(n)} \right|}^2}} - \sum\limits_{n \in {{\rm{I}}_p}} {{{\left| {r(n) - {s_{n - \tau }}{e^{j(2\pi \varepsilon n/N + \theta)}}} \right|}^2}} \\ & = \mathop {{\rm{argmax}}}\limits_{(\tau ,\varepsilon ,\theta)} \left\{ {2{\rm{Re}}\left\{ {{e^ - }^{j(2\pi \varepsilon \tau /N + \theta)}\sum\limits_{i = 0}^{N - 1} {r(\tau + i)s_i^{\rm{*}}{e^ - }^{j2\pi \varepsilon i/N}} } \right\} - {\rho _1}\sum\limits_{i = 0}^{N - 1} {{{\left| {r(\tau + i)} \right|}^2}} - {\rm{c}}} \right\} \end{aligned} $ | (9) |
这里
| $c = {\rho _0}\sum\limits_{i = 0}^{MN - 1} {{{\left| {r(i)} \right|}^2}} + \sum\limits_{i = 0}^{N - 1} {{{\left| {{s_i}} \right|}^2}}$ | (10) |
不难发现, 对于任意给定的
| $2\left| {\sum\limits_{i = 0}^{N - 1} {r(\tau + i)s_i^{\rm{*}}{e^ - }^{j2\pi \varepsilon i/N}} } \right| - {\rho _1}\sum\limits_{i = 0}^{N - 1} {{{\left| {r(\tau + i)} \right|}^2}} - c$ | (11) |
其条件是:
| $\theta = - \frac{{2\pi \varepsilon \tau }}{N} + \angle \left\{ {\sum\limits_{i = 0}^{N - 1} {r(\tau + i)s_i^{\rm{*}}{e^ - }^{j2\pi \varepsilon i/N}} } \right\}$ | (12) |
其中,
| $\left( {{\tau _o},{\varepsilon _o}} \right)\! =\! \mathop {{\rm{argmax}}}\limits_{(\tau ,\varepsilon)} \left\{\!\! {2\left| {\sum\limits_{i = 0}^{N - 1} {r(\tau \!+\! i)s_i^{*}{e^ - }^{j2\pi \varepsilon i/N}} } \right| \!- \!{\rho _1}\sum\limits_{i = 0}^{N - 1} {{{\left| {r(\tau \!+\! i)} \right|}^2}} } \!\!\right\}$ | (13) |
值得注意的是, 式(13)中的参数
| $\left( {{\tau _o},{\varepsilon _o}} \right)\mathop { = {\rm{argmax}}}\limits_{(\tau ,\varepsilon)} \left\{ {\left| {\sum\limits_{i = 0}^{N - 1} {r(\tau + i)s_i^{\rm{*}}{e^ - }^{j2\pi \varepsilon i/N}} } \right|} \right\}$ | (14) |
在载波频偏可以被忽略的OFDM应用中, 例如数字用户线(Digital Subscriber Line, DSL), 此时式(14)给出的时偏和频偏的联合估计
可以发现, 式(14)右边绝对值符号内的操作在本质上是对信号
| $\hat \tau \mathop { = {\rm{argmax}}}\limits_d \left\{ {M(d)} \right\}$ | (15) |
其中,
| $M(d) = {\rm{max}}\left\{ {\left| {\sum\limits_{i = 0}^{N - 1} {r(d + i)s_i^{\rm{*}}{e^{ - j\frac{{2\pi }}{N}ki}}} } \right|,0 \le k < N} \right\}$ | (16) |
是定时测度函数.
2.3 算法复杂度分析除了定时精度, 算法的计算复杂度也具有重要的工程意义. 这里通过比较不同时偏估计器的定时测度函数所需的乘法和加法的数量来评估同步算法的复杂性. 在OFDM系统中, 子载波数总是设置为2的整数次幂, 以便于使用FFT/IFFT操作来实现信号的调制与解调. 因此, 式(16)中的DFT也可以通过FFT来实现, 这极大地降低了计算复杂度.
为了使分析更为直观, 重写式(16)给出的定时测度函数如下:
| $M(d) = \max \{ |({R_d}\circ {S^*})W_k^{\rm{H}}|,0 \le k < {\rm{N}}\} $ | (17) |
其中,
| ${R_d} = [r(d),r(d + 1),\cdots,r(d + N - 1)]$ | (18) |
| ${W_k} = [1,{e^{j\tfrac{{2\pi }}{N}k}},{e^{j\frac{{2\pi }}{N}2k}},\cdots,{e^{j\tfrac{{2\pi }}{N}(N - 1)k}}]$ | (19) |
其中,
接下来评估对于给定的考察点
表1给出了本文提出算法与其他算法计算复杂的对比. 应该注意到, 尽管新算法的计算复杂度高于文献[2,6,9]中提出的算法, 但新算法的定时精确性远高于这些算法, 详细比较将在后文给出. 对于文献[10]中的算法, 该算法允许接收机根据接收信号的信噪比决定采用多少乘积项来构建定时测度函数, 具体来说, 该算法通过设置矩阵
| 表 1 不同算法计算复杂度比较 |
3 仿真及结果
这里采用蒙特卡罗仿真对所提出的算法与现有算法进行对比. 在仿真中, OFDM系统的子载波数设置为64、循环前缀长度为符号长度的1/8 (
图1绘出了本文所提方法与几种现有方法在SUI-1信道下的定时估计MSE的比较. 可以看出, 新提出的方法比以前的方法具有明显更好的性能. 值得一提的是, 即使HM算法将所有的相关乘积项都采用(算法复杂度达到最大), 其定时精度也弱于本文提出的算法. 此外可以看到, 受CFO的影响, 文献[6]和文献[8]的定时估计均方误差很大.
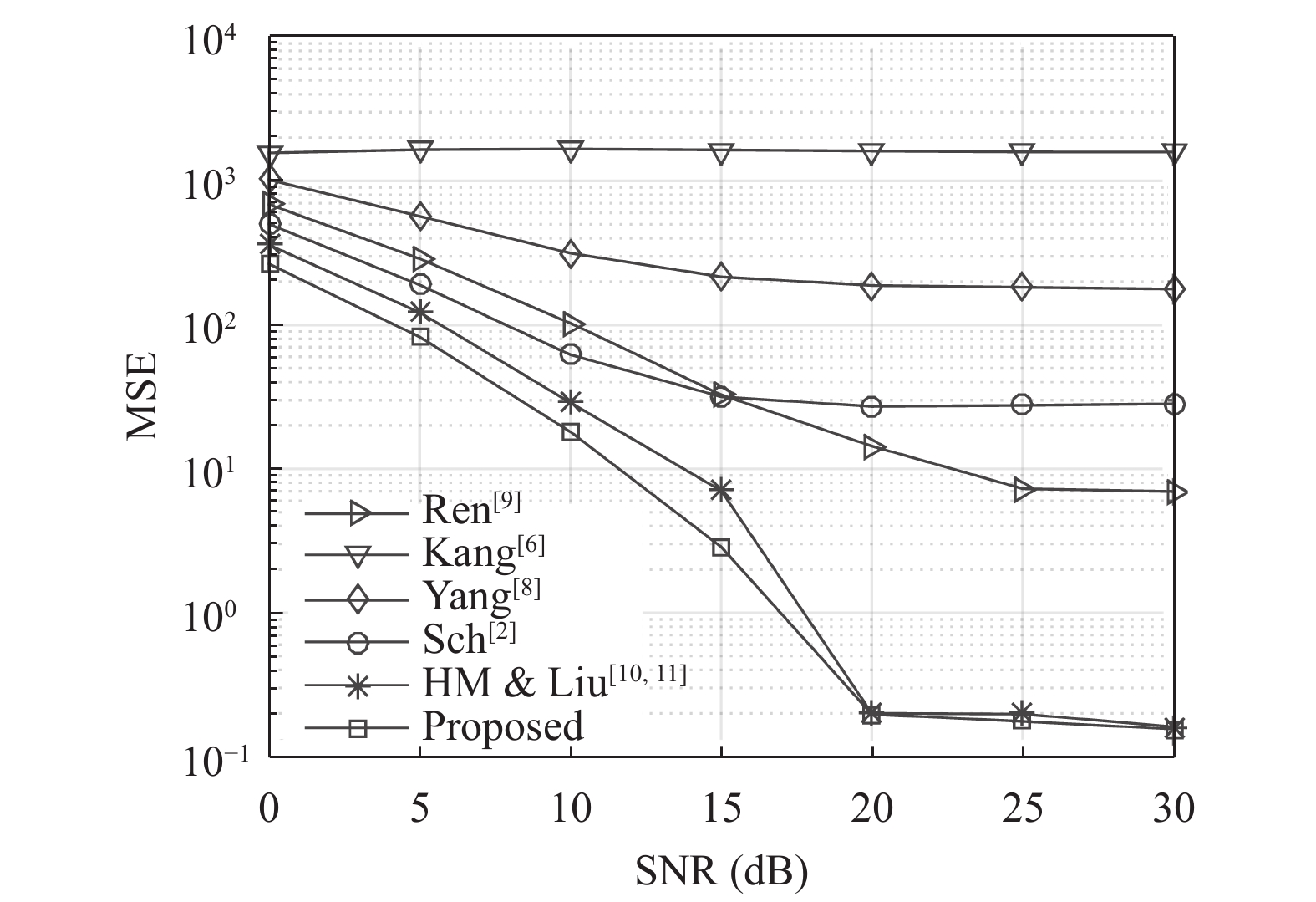
|
图 1 在SUI信道下不同定时算法的MSE对比 |
图2绘出了在一个具有5个抽头的频率选择性瑞利衰落信道中不同估计器的MSE, 抽头序号记为
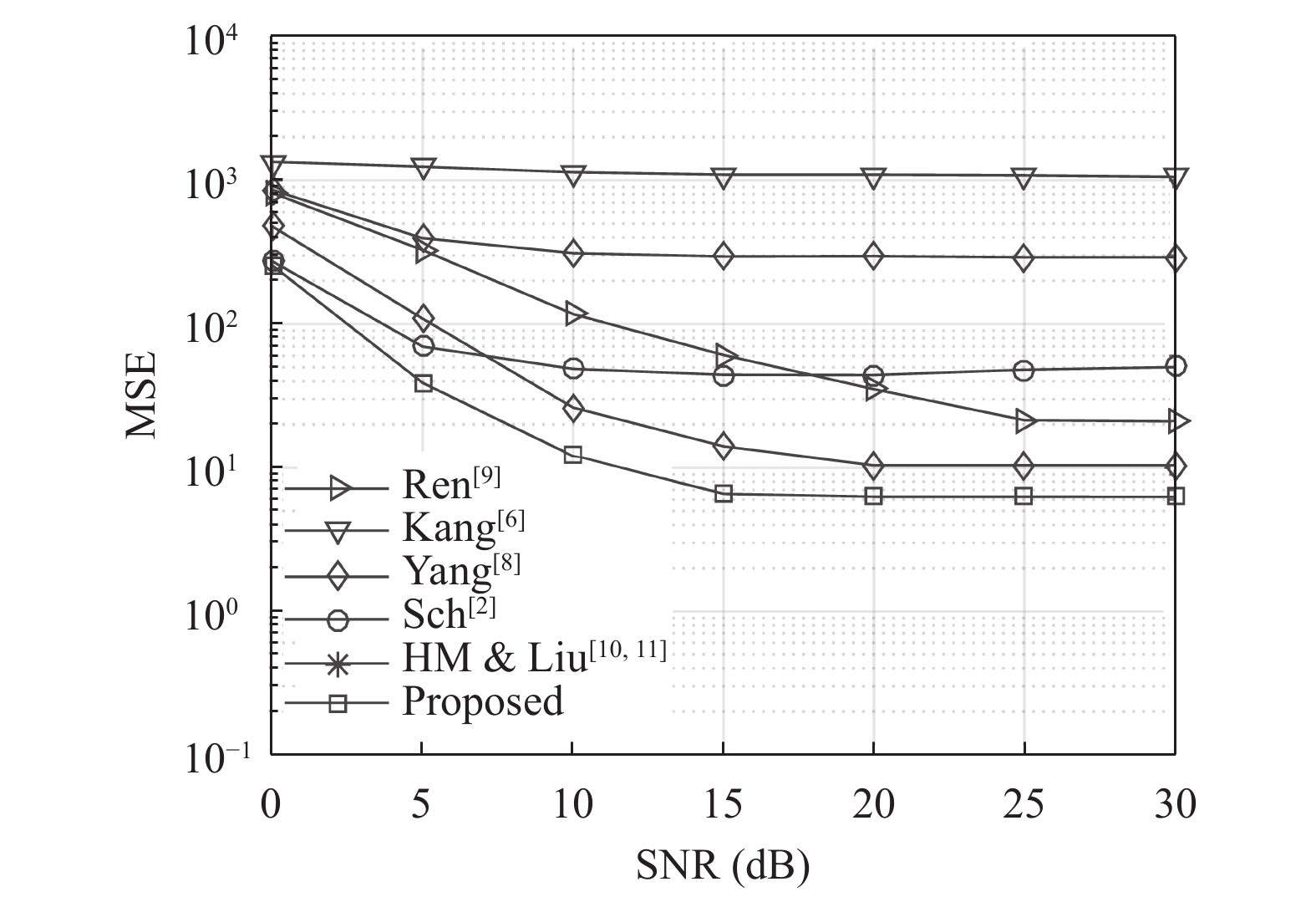
|
图 2 在一个5抽头多径信道下不同算法的MSE |
4 结语
本文中先推导了OFDM系统的定时偏移和载波频偏的ML联合估计, 然后, 基于ML估计器提出了简化的定时同步方法. 所提出的定时方法对辅助数据结构没有特殊要求, 并且对子载波频偏不敏感, 可以在任何数值的载波频偏下实现定时同步. 仿真结果表明, 本同步算法优于现有算法.
| [1] |
Parekha CD, Patel JM. Overview on synchronization in OFDM systems. Proceedings of 2016 International Conference on Advances in Computing, Communication, & Automation. Dehradun, India. 2016. 1–6.
|
| [2] |
Schmidl TM, Cox DC. Robust frequency and timing synchronization for OFDM. IEEE Transactions on Communications, 1997, 45(12): 1613-1621. DOI:10.1109/26.650240 |
| [3] |
Minn H, Zeng M, Bhargava VK. On timing offset estimation for OFDM systems. IEEE Communications Letters, 2000, 4(7): 242-244. DOI:10.1109/4234.852929 |
| [4] |
Shi K, Serpedin E. Coarse frame and carrier synchronization of OFDM systems: A new metric and comparison. IEEE Transactions on wireless Communications, 2004, 3(4): 1271-1284. DOI:10.1109/TWC.2004.828282 |
| [5] |
Park B, Cheon H, Kang C, et al. A novel timing estimation method for OFDM systems. IEEE Communications Letters, 2003, 7(5): 239-241. DOI:10.1109/LCOMM.2003.812181 |
| [6] |
Kang Y, Kim S, Ahn D, et al. Timing estimation for OFDM systems by using a correlation sequence of preamble. IEEE Transactions on Consumer Electronics, 2008, 54(4): 1600-1608. DOI:10.1109/TCE.2008.4711208 |
| [7] |
Abdzadeh-Ziabari H, Shayesteh MG, Manaffar M. An improved timing estimation method for OFDM systems. IEEE Transactions on Consumer Electronics, 2010, 56(4): 2098-2105. DOI:10.1109/TCE.2010.5681078 |
| [8] |
Yang F, Zhang X. Robust time-domain fine symbol synchronization for OFDM-based packet transmission using CAZAC preamble. Proceedings of 2013 IEEE Military Communications Conference. San Diego, CA, USA. 2013. 436–440.
|
| [9] |
Ren GL, Chang YL, Zhang H, et al. Synchronization method based on a new constant envelop preamble for OFDM systems. IEEE Transactions on Broadcasting, 2005, 51(1): 139-143. DOI:10.1109/TBC.2004.842520 |
| [10] |
Abdzadeh-Ziabari H, Shayesteh MG. Robust timing and frequency synchronization for OFDM systems. IEEE Transactions on Vehicular Technology, 2011, 60(8): 3646-3656. DOI:10.1109/TVT.2011.2163194 |
| [11] |
Liu Y, Yu H, Ji F, et al. Robust timing estimation method for OFDM systems with reduced complexity. IEEE Communications Letters, 2014, 18(11): 1959-1962. DOI:10.1109/LCOMM.2014.2358234 |
| [12] |
Van De Beek JJ, Sandell M, Borjesson PO. ML estimation of time and frequency offset in OFDM systems. IEEE Transactions on Signal Processing, 1997, 45(7): 1800-1805. DOI:10.1109/78.599949 |
| [13] |
Chin WL. ML estimation of timing and frequency offsets using distinctive correlation characteristics of OFDM signals over dispersive fading channels. IEEE Transactions on Vehicular Technology, 2011, 60(2): 444-456. DOI:10.1109/TVT.2010.2102058 |
| [14] |
Choi JW, Lee J, Zhao Q, et al. Joint ml estimation of frame timing and carrier frequency offset for OFDM systems employing time-domain repeated preamble. IEEE Transactions on Wireless Communications, 2010, 9(1): 311-317. DOI:10.1109/TWC.2010.01.090674 |
 2020, Vol. 29
2020, Vol. 29


