1 引言 1.1 研究背景

树木是户外场景的重要组成部分, 广泛地应用在虚拟地理环境, 电脑游戏, 城市仿真等领域中. 真实感较强的树木或植被模型能大大提高场景的真实感以及角色的沉浸式体验^[1-3]. 但由于树木具有复杂的拓扑结构以及丰富的几何细节, 需要大量的几何图元进行表达, 因此对树木有效的渲染是计算机图形学领域内十分富有挑战性的课题^[4,5]. 尽管计算机软硬件在近几十年间快速发展, 但仍然远远不能满足绘制复杂虚拟环境的需求^[6]. 对于包含大量树木的森林场景, 其中的数据量将轻易超出可使用的内存, 同时对所有数据的渲染也将大大超出GPU的负荷. 为了提高场景中存在大量数据时的渲染效率, 许多学者分别提出了相应的细节层次(Level Of Detail, LOD)模型^[7-9], 其主要思想是根据几何模型在三维场景中所处的不同位置、重要程度来适当降低非重要物体的几何细节, 从而获得更高效率的渲染效率. 对于树枝来说, 一般用多边形棱柱来表达其几何形状, 通过在横向和纵向上改变多边形棱柱的细分程度构建不同细节层次的树枝模型^[9-11]; 而对于树叶模型, 一般由包含两个三角形的四边形构成^[8,12,13], 其结构简单、相互独立且数量众多, 这三个特点使得对树叶进行实时简化十分富有挑战性^[14].

1.2 国内外研究现状

为了对存在大量离散树叶的树木进行有效简化, 许多学者提出了多种简化算法. 2002~2009年, 有学者通过迭代得合并两个树叶以对树木进行简化. Remolar等提出了第一个用于树叶简化的算法(Foliage Simplification Algorithm, FSA)^[12,15]. FSA算法选择两片树叶作为输入, 然后通过一个成本函数来控制树叶的合并, 进而生成一个可以大致保持原先两片树叶形状的新树叶. 重复执行以上操作即可对树冠进行简化. Zhang等在FSA算法的基础上提出了连续树叶合并(Progressive Leaves Union, PLU)算法^[16], 其改进了FSA算法中的成本函数, 选择更合理的树叶进行合并, 从而获得了更好的简化效果. 上述两种方法只对四边形形状的树叶有效, 且遍历和计算的过程相当耗时. 2006年, Zhang等将由三角形组成的树叶也考虑进来并引入了植物学中的花序, 叶序等概念. 他们使用“分级”的思想对树叶进行简化, 提出了基于植物器官的层次合并(Hierarchical Union of Organs, HUO)算法^[13]. 2009年, Deng等利用树叶密度的概念调整树冠的局部简化率, 叶密度的使用降低了树冠中稀疏部分的简化程度, 可以达到更好的简化效果^[8]. Bao等提出了一种通过使用叶片纹理来简化叶片网格的新方法^[17]. Zhang等提出了一种基于信息论的误差测量方法来测量树叶合并前后的几何误差, 从而可以生成较好的树木LOD模型^[18]. 尽管上述方法可以迭代得合并树叶从而大幅减少渲染数据量, 但往往难以取得较好的可视化效果, 尤其是当简化程度很高时, 树冠会出现严重的“失真”现象. 此外, 由于合并过程中的计算量较大, 这一类方法并不适用于对树叶的实时简化.

另一类值得提起的树叶简化方法是基于随机裁剪的树叶简化方法^[19,20]. 随机裁剪算法假定树冠中的树叶有着相同的重要程度, 在简化过程中对树叶进行随机的裁剪. 基于此, 很多学者进行了相关的研究并提出了相应的方法. Gumbau等提出了一种新颖的基于视点的树叶裁剪算法^[14]. 得益于在预处理过程中对树木中每个单元可见性的量化, 该算法的主要优势是被遮挡的更严重的树叶单元有着更高的简化程度. Bao等针对大规模的植物场景提出了一种优化的随机裁剪算法并引入了精确率与召回率(Precision and Recall, PR)作为衡量简化后视觉质量的指标^[17].

在大部分情况下, 利用随机裁剪算法可以取得较好的简化效果. 但是考虑到树木中的树叶在面积、朝向以及在树冠中的位置的不同, 不同的树叶实际上有着不同的重要度. Gasch等使用视点互信息(Viewpoint Mutual Information, VMI)的变化作为一个新的指标来衡量树叶简化过程中某一树叶被裁剪的视觉影响与依此判定树叶被裁剪的优先级^[21]. 实验结果表明基于VMI的树叶简化可以更好地保持树冠的外部轮廓,同时加大对内部树叶的简化程度.

针对大规模的森林场景渲染, 基于图像的绘制方法(Image Based on Render, IBR)可以将远处的树木几何模型用图像代替, 从而降低渲染负担, 提升渲染效率^[22,23]. 但IBR方法一般只适用于中距离或者远距离的树木渲染. 当视点距离观察对象较近时, 由于图像分辨率有限, IBR方法往往难以取得较好的可视化效果. 此外, IBR方法往往难以对光照、阴影, 树木摇曳等动态效果进行仿真与模拟^[6,24]. 另外一些学者将传统基于几何的方法与IBR方法相结合, 可以在可视化效果与渲染效率之间达到一定的平衡^[25,26]. 但树木由图像转变为几何物体时, 屏幕上往往会出现较为严重的跳变感.

1.3 研究方法概述

本文提出了一种新颖的基于视点互信息的树木实时简化算法. 在预处理阶段首先对树木建模并根据树枝间的拓扑关系将树木划分为多个节点, 然后计算节点中每片树叶的重要度并对树叶进行排序, 简化过程中重要度较低的树叶将优先被简化. 在实时浏览过程中, 根据多个影响因子计算节点的简化率, 据此在每一帧中选取出每个节点中最重要的数据进行渲染. 通过这种方法, 在取得较高简化率的同时较好的保持了树木的几何形状与外观特征, 并有效降低了不同LOD切换时的跳变感. 在实时运行阶段还使用了一些优化的措施, 使得本研究在渲染效率和可视化效果之间达到较好的平衡.

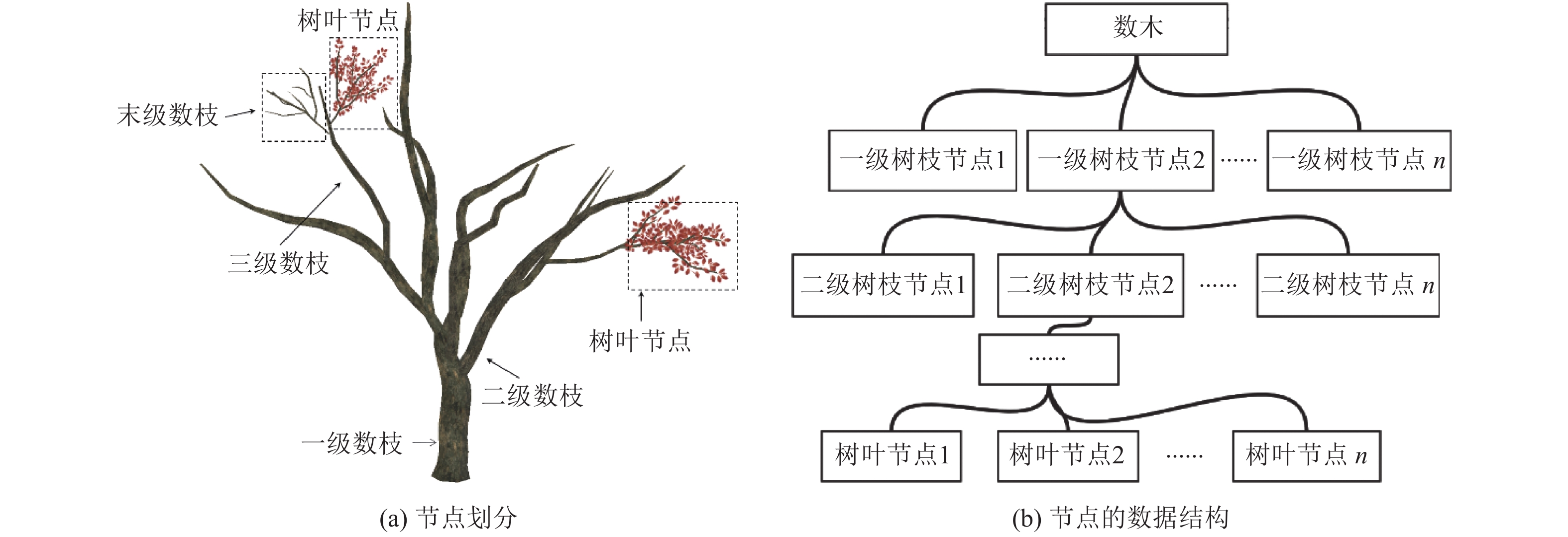
2 基于VMI的树叶简化算法 2.1 节点划分

在预处理过程中首先根据树枝间的拓扑关系将树木划分为具有父子关系的节点. 如图1所示, 每个树枝都由一个节点表示, 树枝节点具有树枝层级的属性, 树干的树枝层级为1, 后续层级的树枝依次递增1. 末级树枝下的子节点包括了所有在该树枝上生长的树叶. 节点数据以多叉树结构组织. 这样的树状数据结构使我们可以通过父节点方便地控制子节点的简化率、渲染状态等信息, 同时可以在渲染时对drawing call进行合并, 从而可以大大减少CPU与GPU间的通信.

2.2 基于VMI的树叶排序

VMI的概念由Castellό等在2008年首次提出^[27], 其基于信息论中互信息的概念, 衡量视点与物体面片之间的相关性. VMI的主要优点在于以下两个方面: (1) VMI对物体形变十分敏感, 与视觉感受有很强的相关性,可以更好的保持外部轮廓信息; (2) VMI可以更好的简化树冠内部因遮挡而不可见的树叶. 因此, 利用VMI对树叶节点进行重要度排序, 可以在达到较高简化率的同时保持与原模型的视觉相似性.

假设视点集合为 $V$ , 以相同的概率均匀分布在物体四周, 则 $V$ 的边缘概率为 $p\left( v \right) = 1/{N_v}$ , ${N_v}$ 为视点个数. 物体面片的集合设为 $O$ , ${a_o}$ 为面片 $o$ 在以视点 $v$ 为球心的球面上的投影面积, ${a_t} = \displaystyle\sum\limits_{o \in O} {a_o}$ , 它表示在视点 $v$ 下所有面片投影面积之和, 则面片 $o$ 在视点 $v$ 下的可见性的条件概率 $p\left( {o|v} \right) = {a_o}/{a_t}$ , 由此得出面片 $o$ 在所有视点下的平均可见性为:

$p\left( o \right) = \mathop \sum \limits_{v \in V} p\left( v \right)*p(o|v) = \frac{1}{{{N_v}}}*\mathop \sum \limits_{v \in V} p(o|v)$

(1)

需要注意的是, 投影面积 ${a_o}$ 指的是面片 $o$ 投影面积中可见的那一部分. 如果一个面片 $o'$ 完全被遮挡, 则 $o'$ 的投影面积为0. 最后, 即可得出VMI的定义如式(2), 其反映了物体面片集合 $O$ 在某一视点 $v$ 下的整体可见性.

$I\left( {v,O} \right) = \mathop \sum \limits_{o \in O} p\left( {o{\rm{|}}v} \right)*\log\frac{{p\left( {o{\rm{|}}v} \right)}}{{p\left( o \right)}}$

(2)

VMI对物体外部的面片非常敏感, 相比于内部被遮挡的树叶, 当外部的一片树叶被裁剪掉时, VMI值会变化更大, 因此可用来衡量节点中树叶的视觉重要程度. 当一个节点因简化从 $O$ 变为 $O'$ 时, 由此带来的VMI误差为:

${e_{\rm VMI}} = \mathop \sum \limits_{v \in V} \left| {I\left( {v,O} \right) - I\left( {v,O'} \right)} \right|$

(3)

为了实时运行阶段的树叶简化顺序更加合理, 我们在预处理中首先根据VMI对树叶按照视觉重要度进行排序. 在计算过程中, 每个树叶节点都会被看作一个包含多片树叶的物体 $O$ , 这些节点在预处理过程和实时简化过程中均相互独立. 在对树叶按照重要度排序的过程中, 每次选取 ${e_{\rm VMI}}$ 最大的树叶作为最重要的树叶. 需要注意的是, 由于一个树叶被裁剪掉之后可能会影响其它树叶的可见性, 因此每当一个树叶被裁剪掉, 需要重新进行VMI的计算.

2.3 实时简化率计算与渲染数据确定

为了使不必要的几何数据不被渲染, 在每一帧都会为每一个节点计算简化率 ${R_s}$ 以确定其LOD. 为了能够准确计算出节点的简化率, 本研究综合考虑了以下影响因子: 包围球层级(Bounding Sphere Level, BSL)、树枝层级(Branch Level, BL)、树叶密度(Leaf Density, LD)、视距(dis)、树枝方向与视线方向的夹角(dir). 在实时浏览时, BSL、BL的值不会发生变化, LD等于初始叶密度乘以当前简化率, dis、dir这两个影响因子则会随着视角、节点的不同而不同. 节点最终的简化率的计算公式如下:

$ \begin{split} {R_s} = & {\alpha _1}*{f_1}\left( {BSL} \right) + {\alpha _2}*{f_2}\left( {BL,dist} \right) + {\alpha _3}*{f_3}\left( {LD} \right)\\ &+{\alpha _4}*{f_4}\left( {dist} \right) + {\alpha _5}*{f_5}\left( {dir} \right) \end{split} $

(4)

其中, ${f_1}\left( {BSL} \right)$ , ${f_2}\left( {BL,dist} \right)$ 等函数代表根据相应的影响因子计算出的简化程度; ${\alpha _1}$ , ${\alpha _2}$ 等参数表示各个函数的权重且 ${\alpha _1} + {\alpha _2} + {\alpha _3} + {\alpha _4} + {\alpha _5} = 1$ . 各个简化函数的定义如下:

${f_1}\left( {BSL} \right) = \left\{ {\begin{array}{*{20}{c}} {0.0,\;BSL = 1} \\ {0.4,\;BSL = 2} \\ {0.8,\;BSL = 3} \end{array}} \right.$

(5)

这里BSL值表示节点在树冠包围球中靠近树冠中心的程度. 由于内部的节点往往被外部的节点所遮挡, 因此相同条件下, 内部节点应比外部节点的简化率高. $BSL = 1$ 时表示该节点暴露在树冠包围球的最外部, ${f_1}\left( {BSL} \right)$ 的值为0.0; $BSL = 3$ 时表示节点在树冠内部, 此时该节点被遮挡严重, ${f_1}\left( {BSL} \right)$ 应取较高值以降低不必要的渲染; 值为2时介于两者之间, 对应的函数值为0.4.

浏览者在近处和远处的观察重点并不一致. 在近处浏览者更多的关注视觉上的细节, 但随着视距拉远, 树木的细节逐渐模糊, 浏览者变得对树木整体结构的变化更加敏感. 为了与浏览者的关注重点一致, 本研究中利用 ${f_2}\left( {BL,dist} \right)$ 函数调节节点在近处和远处的简化策略,保证远距离观察时的视觉效果, 其定义如下:

${f_2}\left( {BL,dis} \right) = \left\{ {\begin{array}{*{20}{l}} {0.0,\;dist \le near} \\ {{k_1}*BL*\log{_h}dis,\;dis \in \left( {near,far} \right)} \\ {0.5,\;dist > far} \end{array}} \right.$

(6)

上述公式确定了在不同的视距下, 树枝参数如何影响简化率. $near$ , $far$ 分别代表视点到最精细与最粗糙LOD模型对应的距离. 当视距大于 $near$ 且小于 $far$ 时, 对于生长在BL值为1, 2, 3树枝节点上的树叶节点, 适当降低其简化率以保持树木的整体特征. 参数h控制 ${f_2}\left( {BL,dist} \right)$ 随距离变化的幅度; 参数 ${k_1}$ 保证 ${f_2}\left( {BL,dis} \right)$ 的结果不大于0.5.

${f_3}\left( {LD} \right)$ 函数用来控制稀疏的树叶节点不会被过度简化. 叶密度LD等于初始叶密度乘以简化率, 其中初始叶密度为:

$ld = \frac{{nu{m_{\rm leaves}}}}{{le{n_{\rm branch}}}}$

(7)

其中, $nu{m_{\rm leaves}}$ , $le{n_{\rm branch}}$ 分别代表初始模型中节点个数以及树枝长度, 这两个参数均可以在建模时得到. $f\left( {LD} \right)$ 的定义如下:

${f_3}\left( {LD} \right) = {k_2}*\left( {LD - ld0} \right)$

(8)

其中, $ld0 = \min\left( {ld1,0.5*ld2} \right)$ , $ld1$ , $ld2$ 分别表示初始树叶节点中的最低叶密度和平均叶密度; ${k_2} = 1/ld0$ . 当叶密度大于 $ld0$ 时, ${f_3}\left( {LD} \right)$ 为正数, 树叶密度促进节点的简化; 当叶密度小于 $ld0$ 时, ${f_3}\left( {LD} \right)$ 为正数, 树叶密度对简化率呈抑制作用.

距离参数对简化率的影响是最直接的, 也是最大的. ${f_4}\left( {dist} \right)$ 的定义如下:

${f_4}\left( {dist} \right) = \left\{ {\begin{array}{*{20}{l}} {0.0,\;dist \le near} \\ {{k_3}*{\rm{log}_{10}}dist,\;dist \in \left( {near,far} \right)} \\ {1.0,\;dist \ge far} \end{array}} \right.$

(9)

其中, ${k_3} = 1/\log{_{10}}far$ . 距离与简化率的对数关系降低了距离在远处的影响.

为实现视点相关的简化, 本研究中利用 $dir$ 参数调节节点在不同视角下的简化率, ${f_5}\left( {dir} \right)$ 定义如下:

${f_5}\left( {dir} \right) = \left\{ {\begin{array}{*{20}{l}} {\cos \left( {dir} \right),\;dir \in \left[ {0,\pi /2} \right]} \\ {0,\;dir \in \left[ {\pi /2,\pi } \right]} \end{array}} \right.$

(10)

其中, $dir$ 代表视线方向 $dir\_eye$ 与树枝节点(对于树叶节点, 则是其父节点)生长方向 $dir\_branch$ 的夹角. 当 $dir$ 处于 $\left[ {0,\pi /2} \right]$ 范围内时, 说明树枝生长在以视点为参考点的树冠的背面, 将被前面的树枝所遮挡, 且 $dir$ 值越大, 树枝被遮挡的通常会越严重; 当 $dir$ 处于 $\left[ {\pi /2,\pi } \right]$ 范围内时, 说明树枝生长在树冠的正面, 此时将 $f\left( {dir} \right)$ 的值置为0.

考虑到距离对简化率的影响最大, 在本研究中令 ${\alpha _4} = 0.3$ , ${\alpha _2} = 0.1$ , ${\alpha _1} = {\alpha _3} = {\alpha _5} = 0.2$ . 在实时运行中的每一帧, 节点最终的简化率将由以上5个简化函数加权得到.

在获得节点的简化率 ${R_s}$ 之后, 接下来要确定哪些数据应该被渲染. 由于树叶在预处理中已经按照重要性从高到低的顺序排列, 因此我们只需要简单地删除最后 $(si{\textit{z}}e\;{\rm{*}}\;|{R_c} - {R_l}|)$ 片树叶即可实现对树叶节点的简化或者细化, 其中 $si{\textit{z}}e$ 表示节点中树叶的数量, ${R_c}$ , ${R_l}$ 分别代表当前帧和上一帧的简化率. 节点的细化过程与简化过程类似, 只需要重新渲染对应的树叶即可实现.

3 渲染优化措施

在渲染大规模森林场景时, 一方面, 场景中存在着大量的几何模型, 这将会消耗大量的内存; 另一方面, 由于场景中节点数量众多, 过多的LOD模型切换使得我们很难在每一帧中为所有的节点计算出准确的LOD并进行有效的渲染. 为了解决上述的效率与内存问题, 本研究在几何着色器中实时放大树叶来保持树冠整体的视觉效果. 为了减少不必要的LOD切换, 本研究提出了一种基于距离的LOD切换控制措施以调节不同节点LOD切换的频率与幅度. 此外, 我们在预处理中生成闭合的树冠轮廓模型以代替远处树木的几何模型, 从而大大降低渲染负担.

3.1 树冠外观保持

当简化率过大时, 往往无法用剩余的树叶较好的表达出原始树冠的视觉效果, 这时可能会给浏览者带来一些视觉上不好的体验, 比如树冠逐渐由树叶的颜色变为树枝的颜色. 但由于此时节点往往距离较远或者被严重遮挡, 因此我们可以在实时运行过程中执行一些补偿措施以弥补简化率较大时的“失真”现象. 在本研究中采用Gumbau等在文献[14]中的提出的策略: 在实时浏览过程中改变树叶面积并保持树叶的总面积大致不变. 对于节点i, 假设其初始状态下树叶个数为n, 所有树叶的总面积为S. 当在某一时刻简化率变为r, 意味着将有 $n \times r$ 片树叶被裁剪掉. 此时树叶的总面积可以近似的表示为 $S*\left( {1 - r} \right)$ . 为弥补由于简化而造成的视觉损失, 我们将剩余的树叶沿树叶的中心向外扩展s倍以保持树叶总面积大致不变, 其中:

$s = sqrt\left( {\left( {1.0 - {R_l}} \right)/\left( {1.0 - {R_c}} \right)} \right)$

(11)

此时该节点的树叶总面积为:

${S_{\rm cur}} = {S_{\rm last}}*s*s$

(12)

其中, ${S_{\rm cur}}$ , ${S_{\rm last}}$ 分别表示节点i在上一帧和当前帧的树叶总面积. 树叶中心的坐标等于树叶的4个顶点的平均值. 上述操作在GPU渲染管线中的几何着色器阶段执行, 几乎不会带来额外的渲染成本.

3.2 基于泊松表面重建算法的树木轮廓模型构建

当照相机距离树木较远时, 此时, 树木内部的细节已经基本不可见, 浏览者此时往往只能注意到树木的整体轮廓. 在浏览场景时, 这些树木模型占据了较多的内存, 但是对浏览者的观感作用有限. 同时, 这些树木中的节点也没有必要进行过多的LOD切换, 否则在电脑屏幕上将会出现一些不断闪烁的“噪点”, 这将给用户带来非常不好的体验.

为了解决上述问题, 本研究在预处理过程中为树木预先构建外部轮廓模型. 这种模型是一种连续的网格结构, 与实际上的树木模型相差较远, 但远距离观察时, 这种简化的轮廓模型与树木整体的形状十分相似, 因此可以在距离较远时代替原始树木模型进行渲染. 具体操作步骤如图2所示: 首先选取所有树枝的顶部端点作为特征点, 其发现方向为树冠中心指向该点的方向. 但是有些特征点会更靠近树冠内部而不是外部轮廓. 为此我们设置一个距离阈值θ, 将所有到树冠中心的距离小于θ的特征点删除, 然后利用泊松表面重建算法^[28,29]生成树冠轮廓模型, 如图2(b)、图2(c). 生成的树冠模型可以比较真实的展现出树冠的整体轮廓, 最后利用边折叠的方式进一步的压缩顶点数量, 最终结果如图2(d)所示. 相比于原先树冠中310 364个顶点, 最终所构建的树冠轮廓模型中仅有744顶点, 降低了渲染负担.

3.3 LOD管理系统

在对LOD切换的实验过程中, 我们发现对近处和远处的节点应采取不同的LOD管理方式. 具体来说: 近处的节点由于更靠近照相机, 在屏幕上往往会占据更多的像素, 因此其LOD变化不应太剧烈, 否则将产生强烈的跳变感; 而对于远处的节点, 由于距离较远且遮挡严重, LOD变化较小时几乎不会被浏览者注意到. 因此对于这些节点, LOD没有必要变化太频繁.

在上述的讨论中, LOD变化的频率与幅度都与距离紧密相关. 在具体的实施过程中, 我们在每一帧中为每个节点记录其简化率的变化 $\Delta rate$ 以及该简化率保持不变的时间 $tim{e_{\rm last}}$ . 只有当 $\Delta rate$ 与 $tim{e_{\rm last}}$ 满足式(13)时, 节点的LOD才会被更新.

$\left\{ {\begin{array}{*{20}{l}} {\Delta rate < {\delta _1}*{{\left( {dist - near} \right)}^{{k_1}}}} \\ {\Delta tim{e_{\rm last}} > {\delta _2}*{{\left( {dist - near} \right)}^{{k_2}}}} \end{array}} \right.$

(13)

式中, ${\delta _1} = 1/{\left( {far - near} \right)^{{k_1}}}$ , ${\delta _2} = 1/{\left( {far - near} \right)^{{k_2}}}$ . ${k_1}$ , ${k_2}$ 均大于0, 分别用来控制 $\Delta rate$ , $\Delta tim{e_{\rm last}}$ 随距离变化的强度.

由于近处节点的距离较小, 此时的 $\Delta rate$ 阈值也较小, 保证了近处节点不会产生视觉上的突变; 而对于远处的节点, $\Delta tim{e_{\rm last}}$ 阈值较大, 这确保了远处的节点不会频繁的改变其细节层次.

4 结果与讨论

本文中三维算法是使用OpenSceneGraph^[30] API开发的, 编程语言为C++. 试验环境为: 2.8 GHz Intel Core i7-7700HQ CPU、16 GB RAM以及NVIDIA GeForce 940MX GPU. 本研究中所使用的树的实验参数列于表1.

4.1 树木可视化效果

为了阐明本文中的方法的合理性, 我们进行了一系列的实验来验证本文中的因子以及优化措施是如何提高效率并改善视觉效果. 图3(a)表示树木的初始状态, 图3(b), 图3(c)分别表示不使用BL参数时树木的简化效果; 对应的, 图3(d), 图3(e)表示使用BL参数时的树木的简化效果. 图3(b)–图3(e)的简化率分别为50%, 80%, 43%, 71%, 从图3中可以看出, 使用BL参数虽然会轻微的增加渲染数据, 但却大大提高了树木的可视化效果.

本研究利用Dir参数实现视点相关的实时树木简化. 如图4所示, 图4(b)–图4(d)展示了夏栎树在简化率为50%, 距离为25 m时各个角度的观察效果. 从图中可以明显看出, 背面的节点相比于正面的节点有着更高的简化率.

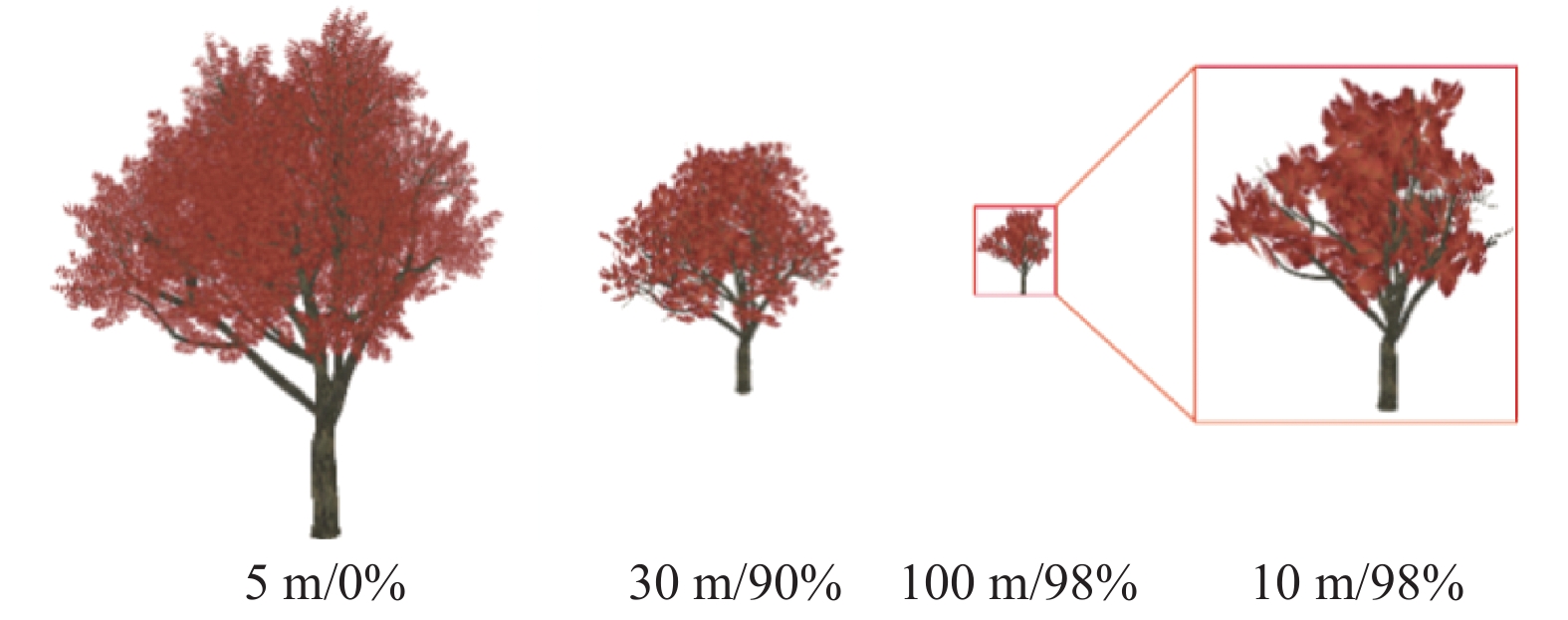
图5展示了在相同的简化程度下, 放大树叶与不放大树叶所造成的效果差异. 从左到右树木的距离与简化率分别为5 m/0%, 30 m/90%, 100 m/98%, 10 m/98%. 显然, 放大之后的树叶可以有效地保持树冠外观在不同LOD下的一致性.

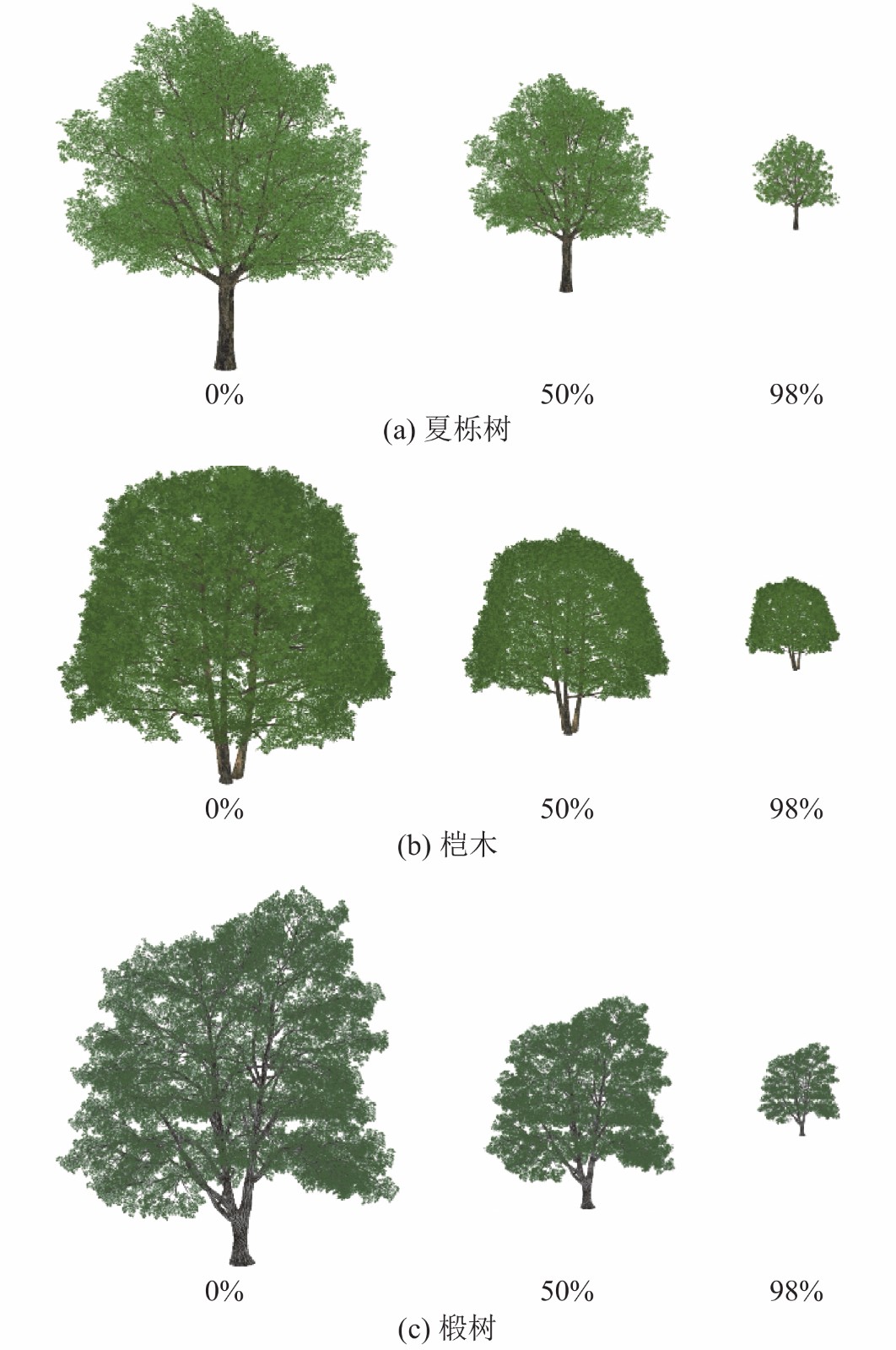
在综合考虑了本文中的所有影响因子之后, 我们为表1中的3种典型树木生成相应的LOD模型. 如图6所示: 自上到下分别是夏栎树, 桤木以及椴树, 从左往右简化率分别为0%, 50%, 98%. 结果表明我们的方法可以在大大降低渲染数据时保持较高的保真度.

由于我们在预处理中为树木生成与原始模型十分相似的三维轮廓模型, 我们可以轻易地渲染出包含大量树木的森林场景. 图7展示了一个包含1660棵树的森林场景, 其中视锥体内共有621棵树, 对应的初始状态下共有4251万个三角形图元. 而在当前帧中仅有199.75万个三角形图元需要渲染, 整个场景的平均简化率为4.7%, 平均帧率为30.21 fps, 是不做任何简化处理的15.18倍.

4.2 对比分析

在森林场景中实时浏览时, 存在两个不可避免的难题. 首先, 表达整个场景所需的几何数据将很容易超出可用内存; 其次, 浏览中大量的LOD切换不仅会导致屏幕闪烁, 而且还会带来很多drawing calls, 这将大大降低渲染效率. 对于第一个问题, 本研究基于泊松表面重建算法, 在预处理中生成了封闭的树木轮廓模型以用于远处树木的渲染. 如图8所示: 第一行以线模式展示了5种树木模型的轮廓模型, 第二行以点模式展示了对应树木的原始形态, 最后一行将两者叠加以展示其形状对比. 表2对比了轮廓模型和原始模型之间的顶点数量. 结合图8以及表2可以看出该方法在保持树的整体形状的同时可以大大降低渲染负担.

为解决第二个问题, 本研究提出了一种基于距离的LOD控制方案, 它使得近处和远处的节点具有不同的LOD转换条件. 这种措施减少了附近节点突然改变的可能性, 并降低了远处节点的LOD转换的频率. 我们的方法对于包含了成千上万个节点的大规模森林场景尤其有效. 在图7的场景中, 与没有LOD转换控制的实验相比, 帧率平均提高了12.6 fps.

得益于在预处理中对树叶按照视觉上的重要程度进行排序, 我们的方法在裁剪树叶的顺序方面比其它树叶简化方法明显更加合理, 因此也有着更好的可视化效果. 图9展示了我们的方法与随机裁剪算法的对比. 从左到右, 分别为树木初始状态, 基于随即裁剪算法的效果以及我们算法的效果, 简化率均为50%. 我们使用PR值定量比较这两种算法的优劣. 基于随机裁剪算法的PR值分别为0.90/0.71、0.92/0.78, 而使用本文中的方法得到的PR值分别为0.95/0.82、0.96/0.88. 从中可以看出, 我们的算法在取得高简化率时可以更好地保持树木的外观特征.

5 总结与展望

我们提出了一种基于VMI的树木实时渲染算法. 我们使用VMI值的变化作为为树叶简化顺序的依据. 在实时运行阶段, 综合考虑遮挡, 视距等因素, 在视觉效果和简化率上达到了较好的平衡. 为了有效处理大规模森林场景中存在的大量LOD变换, 我们提出了一套新的判断准则来决定节点的LOD应该改变. 此外, 我们在预处理中为树木生成闭合的三维轮廓模型以供视距较远时动态加载, 这大大降低了场景中的内存与渲染负担. 实验结果表明我们的方法在渲染效率和可视化效果上都可以取得令人满意的效果.

我们计划在以下方面继续改进我们的研究. 第一, 探索更优或者自动化的参数确定方法以提供更好的简化策略; 其次, 我们将研究如何更高效的利用粗糙的LOD模型取代那些被遮挡的树木; 最后, 我们考虑将本研究中提出的LOD数据结构应用在对树木的网络传输中以降低网络传输和客户端渲染的压力.