2. 海南医学院 公共卫生学院, 海口 571101;
3. 黑龙江大学 数据科学与技术学院, 哈尔滨 150080
2. School of Public Health, Hainan Medical University, Haikou 571101, China;
3. Institute of Data Science and Technology, Heilongjiang University, Harbin 150080, China
图像匹配[1]是计算机视觉中的重要研究技术之一, 是一种图像处理技术. 目前, 图像匹配的两种主流方法可以分为: 基于像素灰度[2]的图像匹配和基于特征[3]的图像匹配. 前者就是逐像素地把一个实时图像窗口的灰度矩阵与参考图像的所有可能的窗口灰度矩阵按某种相似性度量方法进行搜索比较的匹配方法, 包括绝对误差和算法SAD (Sum of Absolute Differences)[4]、误差平方和算法SSD (Sum of Squared Differences)[5]、归一化积相关算法NCC (Normalized Cross Correlation)[6]等, 但是该类匹配算法计算量较大, 且对噪声敏感, 导致匹配效果很差; 基于特征的匹配方法是在原始图像中提取特征, 然后用相似性度量和一些约束条件确定几何变换, 最后将该变换作用于待匹配图像, 包括SUSAN(Small Univalve Segment Assimilating Nucleus)角点检测[7]、Harris角点检测[8]等方法. 现有的基于特征的匹配方法虽然可以解决旋转、平移等问题, 但是, 当存在复杂变化时, 如: 大尺度、光照、模糊等, 都会使得上述方法失效. 2004年, Low提出了一种尺度不变特征变换算法SIFT (Scale Invariant Feature Transform)[9,10], 该算法对尺-度、旋转、缩放、仿射变换等具有不变性, 而且有很好的稳定性和鲁棒性, 但是SIFT算法复杂度较高, 计算量很大, 需要耗费较长时间完成特征描述和匹配. 因此, Bay等针对SIFT算法的不足提出了改进算法SURF (Speeded Up Robust Features), SURF[11,12]算法具有良好的鲁棒性, 速度也比SIFT提高了3倍左右. 但是由于目前的SURF算法存在错误匹配的问题, 使得匹配结果的准确度有所降低, 速度也会由于不稳定特征点及误匹配对的存在而大大减慢, 本文基于SURF提出了一种优化算法, 并通过Matlab语言进行了算法的实现, 分析其在光照、模糊、JPEG压缩变化下的鲁棒性.
1 传统SURF算法特征检测与匹配 1.1 提取特征点SURF算法采用Hessian矩阵行列式来检测特征点, 每一个像素点都可以求出一个Hessian矩阵:
| $H(x,\delta ) = \left[ \begin{array}{l} {L_{xx}}(x,\delta ),{L_{xy}}(x,\delta ) \\ {L_{xy}}(x,\delta ),{L_{yy}}(x,\delta ) \\ \end{array} \right]$ | (1) |
其中, L(x, δ)是经过高斯滤波器、二阶微分在点X=(x, y)处和图像I的卷积. Lxx(x, δ)、Lyy(x, δ)有类似的含义. 为了提高运算速度, SURF使用盒式滤波器(box filter)来近似高斯滤波器, 卷积运算后的值分别为Dxx、Dyy、Dxy, 因此, Hessian矩阵的行列式最终简化为:
| $det(H) = {D_{xx}}*{D_{yy}} - {D_{xy}}*{D_{xy}}$ | (2) |
其中, det(H)表示点X附近区域的盒式滤波响应值, 用它检测极值点. 为了平衡因使用盒式滤波器近似所带来的误差, 在Dxy上乘了一个加权系数ω, ω一般取值为0.9. 因此每个像素的Hessian矩阵判别式的近似值为:
| $det(H) = {D_{xy}}*{D_{yy}} - {(\omega *{D_{xy}})^2}$ | (3) |
盒式滤波器对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题, 只需要简单几次查找积分图就可以完成.
1.2 在尺度空间中实现特征点定位为了获得不同尺度的采样点, 需要构建图像的尺度空间, 在尺度空间上提取特征点. SURF的尺度空间是由O组L层组成, 同一组间不同层间使用相同尺寸的滤波器, 但是滤波器的模糊系数逐渐增大. 如图1所示, 图1(a)是传统方式建立的金字塔结构; 图1(b)是SURF算法的金字塔结构, 它使原始图像保持不变而只改变滤波器大小.

|
图 1 尺度空间对比 |
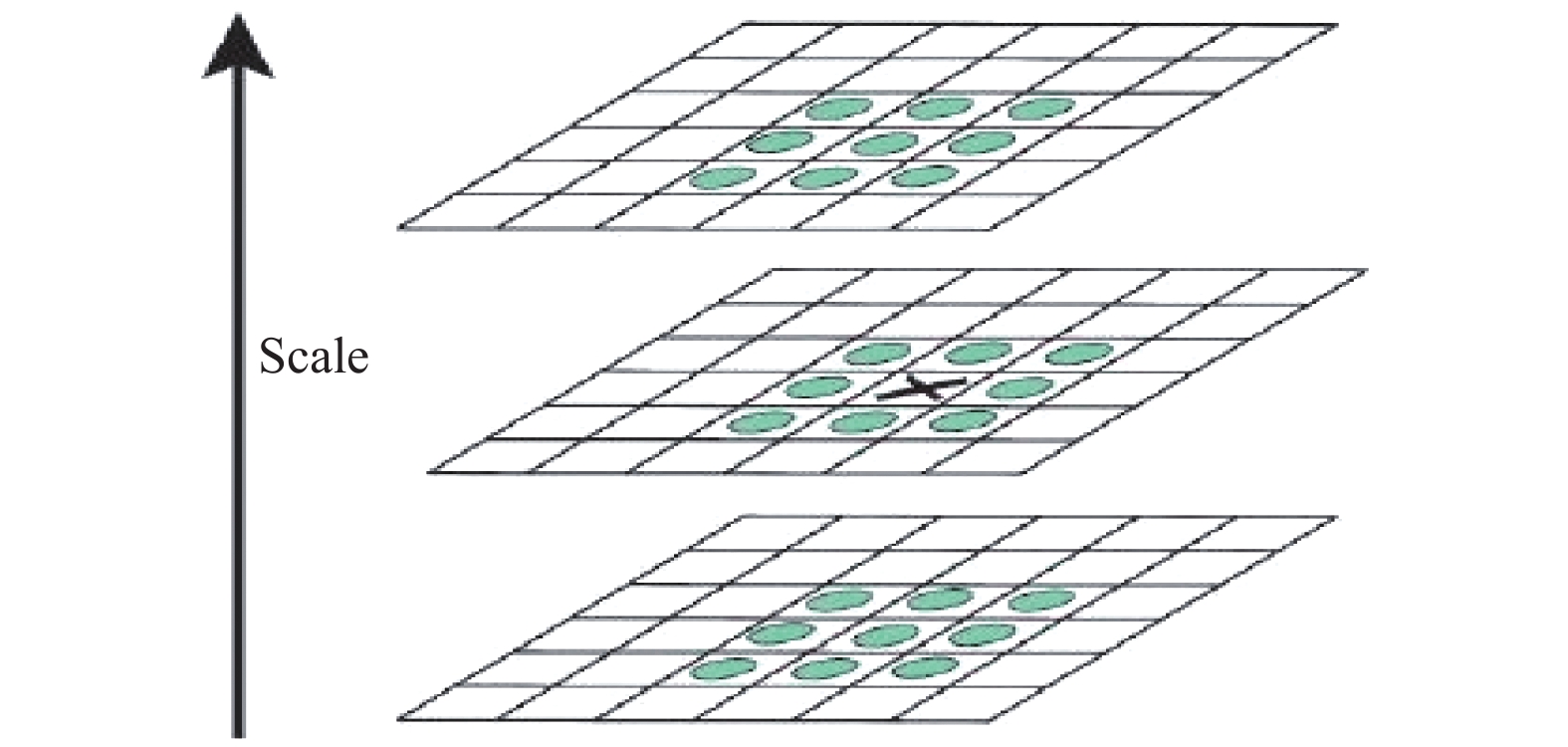
SURF特征点的定位是在不同尺度特征点的响应图像上采用邻域非极大值抑制, 将每个像素点与二维图像空间和尺度空间邻域内的26个点进行比较, 选出特征点候选点; 再利用三维线性插值法对候选点进行定位, 获得亚像素级别的特征点, 由此完成特征点的提取. 具体过程如图2所示.
|
图 2 极值点检测 |
1.3 确定特征点方向
为了满足旋转不变性, 必须确定特征点的主方向. 具体做法是统计特征点领域内的Haar小波特征, 即在特征点的领域内, 统计60度扇形内所有点的水平Haar小波特征和垂直Haar小波特征总和, 这样一个扇形就得到了一个响应值. 将响应值分别加起来, 形成矢量, 选择其中最长的矢量方向, 作为最终特征点的主方向. 该过程的示意图如图3所示.

|
图 3 特征点主方向 |
1.4 构建特征描述子实现匹配
特征点确定之后, 就要根据特征点构建描述子. 具体做法是在特征点周围取一个4×4的矩形区域块, 所取得矩形区域方向是沿着特征点的主方向. 每个子区域统计25个像素的水平方向和垂直方向的Haar小波特征. 把Haar小波值作为每个子块区域的特征向量, 所以一共有4×4×4=64维向量作为SURF特征的描述子. 具体过程见图4.
根据描述子进行特征匹配, 传统SURF是通过计算两个特征点间的欧式距离来确定匹配度, 实现匹配, 欧氏距离越短, 代表两个特征点的匹配度越好.
2 改进的SURF算法SURF算法分为特征检测和特征匹配两个阶段, 在特征检测阶段, 由于存在错误检测, 使得一些误点被检测为特征点, 降低匹配精度. 在匹配阶段, 错误的匹配对的存在, 使得匹配精度降低的同时, 增加了计算量. 本文针对这两个阶段对SURF算法进行了改进, 在特征点检测阶段, 引入图像的局部二维熵[13,14], 从降低冗余信息出发, 实现对不稳定特征点的剔除. 在匹配阶段, 引用曼哈顿距离[15]代替传统的欧式距离, 降低复杂度, 减少计算量, 并引入最近邻和次近邻[16]的概念实现特征匹配. 改进算法和原始SURF算法图像特征匹配流程图如图5所示.

|
图 4 构建特征描述子 |

|
图 5 改进SURF算法和原算法特征匹配对比流程图 |
2.1 基于局部熵的SURF算法特征点检测
图像熵[17], 一种特征的统计形式, 反映了图像中包含平均信息量的多少, 当图像为纯色图时(纯白或者纯黑图), 图像就只包含一种灰度值, 此时熵最小, H=0, 认为图像的信息量为0. 当图像包含多个灰度值时, 也就是说图像每个像素的灰度值都不一样, 此时熵最大, H=
| ${p_{ij}} = f(i,j)/{N^2}$ | (4) |
式(4)能反映某像素位置上的灰度值与其周围像素灰度分布的综合特征, f(i, j)为特征二元组(i, j)出现的频数, N为图像的尺度. 定义离散的图像二维熵为:
| $H = - \sum\limits_{i = 0}^{255} {{p_{ij}}\log{p_{ij}}} $ | (5) |
想要建立图像特征点的局部二维熵[18], 可以在特征点所包含信息量的前提下, 突出反映该像素位置的灰度信息, 以及其邻域内灰度分布的综合特征. 由图像局部熵的特性, 本文根据采样点的局部二维熵来刻画特征点的独特性, 检测真正属于特征的采样点. 特征点的局部邻域二维熵越大, 其与邻域像素灰度值相差越大, 即携带的信息量越大, 特征点则更稳定. 具体策略如下:
(1)选择某一采样点的局部邻域(本文用3×3邻域), 计算该点邻域二维熵, 统计所有SURF提取出的采样点的局部邻域二维熵.
(2)设置合适的阈值, 当采样点的二维熵值大于阈值T1
具体做法是根据二维熵定义计算待匹配图和参考图特征点位置的二维熵值, 假设为Q, 判断其与阈值[T1, T2]的关系, 若Q < T1或者Q > T2,则认为该点不是稳定的点, 予以删除. 通过遍历图像中的所有采样点的二维熵值, 得出大部分的熵值都在[2, 4.5]之间, 当取值小于2或者大于6时, 则难以剔除不稳定的特征点, 故本文选取T1 = 2, T2 = 4.5, 选取阈值范围内的点, 有效剔除一部分不稳定的点.
2.2 基于曼哈顿距离的SURF匹配算法在匹配阶段, SURF 算法是通过计算一幅图像中所有特征点与另外一幅图像中所有特征点之间的欧氏距离来实现. SURF特征描述符是64维, 遍历计算所有对应点的欧式距离, 导致匹配阶段的计算效率极低, 为了减少计算量, 本文从两个方面来提高匹配阶段的效率:
(1)用曼哈顿距离代替欧式距离, 作为衡量特征点描述符相似度的标准, 减少了计算量.
(2)引入最近邻与次近邻比, 减少特征点相似性比较过程中的次数, 降低时间复杂度.
2.2.1 曼哈顿距离代替欧式距离n维点X = (x1, x2, x3, …, xn)与Y = (y1, y2, y3, …, yn)之间的欧式距离定义为:
| ${D_0} = \sqrt {\sum\limits_{i = 1}^n {{{({x_i} - y{}_i)}^2}} } $ | (6) |
二者的曼哈顿距离定义为:
| ${D_1} = \sum\limits_{i = 1}^n {|{x_i} - {y_i}|} $ | (7) |
通过验证我们可以知道, D1 ≥ D0, 而且根据定义不难看出D1的计算比D0简单, SURF的描述符是64维的, 对于每个特征点, 需要计算64次欧式距离, 包含64次减法, 64次平方, 64次加法和一次开方; 对于曼哈顿距离的计算则需要64次减法, 64次绝对值运算和63次加法运算. 显然, 曼哈顿距离比欧式距离少了开方运算, 极大地减少了计算量.
2.2.2 采用最近邻次近邻的特征匹配为了排除因为图像遮挡和背景混乱而产生的无匹配关系的关键点, 引入最近邻距离与次近邻距离比进行匹配: 求取一幅图像中的一个SURF关键点X1, 并找出其与另一幅图像中某一特征点X2的曼哈顿距离, 求其最近邻C1和次近邻C2, 得出C1和C2的比值, 记为
为了验证本文改进算法的鲁棒性, 将Mikolajczyk[19]图像库中的数据作为测试数据, 采用计算机为i5处理器, 4 GB内存, 进行程序开发, 实验验证; 本文用到了数据库中的leuven、trees、ubc图像, 分别在光照、模糊和JPEG压缩等条件下, 对SURF算法、BRISK算法、Harris算法与本文算法在匹配准确率和时间上进行比较分析, 给出了算法的定量评估结果.
3.1 光照条件下鲁棒性比较不同光照下, 图像的某些特征会被弱化, 本实验通过将原图与数据集中亮度变化最大的图进行匹配, 观察结果. 光照变化匹配结果如图6所示, 数据分析如表1所示. 其中, 正确率=(正确匹配对数/总的匹配对数).
由匹配图可知, SURF、BRISK、Harris算法在进行光照变化的匹配时, 都有无序匹配对的存在, 改进后的算法相比于其他算法有更好的匹配效果, 不存在无序匹配连线对.

|
图 6 光照变化匹配效果图 |
| 表 1 图像光照变化匹配结果分析 |
分析表中数据易知, 由于leuven图像光照变化较大, 使得算法在待匹配图中检测到较少的特征点. SURF算法在特征检测阶段没有剔除不稳定点, BRISK、Harris及改进后的算法对光照变化条件下的图像能有效检测特征点, 并在特征点检测阶段剔除部分不稳定的点; 在匹配阶段各个算法均对误匹配点进行了剔除. 观察数据可知本文算法与SURF、BRISK、Harris相比, 速度加快的同时正确率也得到了提高.
3.2 模糊条件下鲁棒性比较图像模糊处理后, 分辨率会降低, 特征点的识别度也会随之下降, 本实验用数据集中模糊度最高的的图像与原图匹配, 实验结果如图7所示, 数据分析如表2所示. 其中, 正确率=(正确匹配对数/总的匹配对数).
从匹配结果中可以看出, 对于模糊条件下的匹配, SURF、BRISK、Harris算法匹配效果都变得有些无序, 本文改进的算法, 表现出更好的优势, 几乎不存在无序匹配对, 直观上来看匹配效果达到最好.
分析表2中的数据, 由数据可知, 在对模糊图像进行特征检测时, 由于trees图像模糊度较大, 在待匹配图中检测到的特征点数目较少. 观察数据可知SURF算法在特征点检测阶段没有进行误点的剔除, BRISK、Harris和本文改进后的算法对模糊条件下的图像进行匹配时, 能有效检测特征点并在特征点检测阶段剔除部分不稳定的特征点, 在匹配阶段, 各算法都剔除部分误匹配点. 本文算法在速度上相比于SURF有所加快, 与BRISK、Harris算法几乎相当, 正确率比SURF算法高出将近20%, 比BRISK、Harris稍高, 因此可以看出在处理模糊变化的图像时, 本文算法有更好的鲁棒性.

|
图 7 模糊变化匹配效果图 |
| 表 2 图像模糊变化匹配结果分析 |
3.3 JPEG压缩条件下鲁棒性比较
对图像进行JPEG压缩, 会使得图像信息发生变化, JPEG压缩属于有损压缩, 去掉了视角的冗余信息和数据本身的冗余信息, 对压缩处理最严重的图像与原图匹配, 各个算法结果如图8所示. 数据分析总结如表3所示. 其中, 正确率=(正确匹配对数/总的匹配对数).
观察匹配结果图, 对于JPEG压缩条件下的图像匹配, 几种算法都达到良好的效果, SURF和BRISK存在少量错误无序匹配, Harris相比之下无序对数较多, 改进后的算法几乎无无序匹配对, 匹配效果达到最好.
分析数据如表3所示, 由数据可知, SURF在特征点检测阶段没有进行不稳定点的剔除, BRISK、Harris和改进后的算法对JPEG条件下的图像匹配能有效检测特征点并剔除部分误点, 由于JPEG压缩改变了图像的信息, 因此改进算法采用局部熵对误点进行剔除时, 能剔除更多无效的点; 在匹配阶段各个算法都进行了误匹配点的剔除. 可以看到改进后的算法与其他算法相比, 正确率得到提高的同时, 也减少了计算量.

|
图 8 JPEG压缩鲁棒性效果图 |
| 表 3 JPEG压缩变化下的匹配结果分析 |
4 总结
本文在传统SURF算法图像匹配的基础上, 提出了一种改进算法, 特征提取阶段, 结合了局部二维熵, 用于剔除误点; 特征匹配阶段, 用曼哈顿距离代替欧式距离, 降低计算复杂度, 并引入了最近邻和次近邻比实现匹配. 实验结果表明, 改进后的算法能够有效剔除误点, 减少误匹配, 降低匹配时间, 与传统算法相比, 本文算法有很好的鲁棒性和准确率.
| [1] |
戴涛, 朱长仁, 胡树平. 图像匹配技术综述. 数字技术与应用, 2012(3): 174-175, 177. |
| [2] |
Hu JW. Fast image matching algorithm based on pixel gray value. Proceedings of the 2017 5th International Conference on Frontiers of Manufacturing Science and Measuring Technology. Taiyuan, China. 2017. 166.
|
| [3] |
陶静, 李逸琳, 霍艺文, 等. 基于特征点匹配的图像配准研究. 现代电子技术, 2019, 42(20): 90-93. |
| [4] |
李养胜, 李俊. 基于角点检测与特征点配准的图像拼接算法. 舰船电子工程, 2018, 38(4): 69-72. |
| [5] |
汪宋, 费树岷. SSD(Single Shot MultiBox Detector)目标检测算法的研究与改进. 工业控制计算机, 2019, 32(4): 103-105. |
| [6] |
杨通钰, 彭国华. 基于NCC的图像匹配快速算法. 现代电子技术, 2010, 33(22): 107-109. |
| [7] |
崔乐, 李春, 李英. Harris算法和Susan算法的实现及分析. 计算机与数字工程, 2019, 47(10): 2396-2401. |
| [8] |
韩松奇, 于微波, 杨宏涛, 等. 改进Harris角点检测算法. 长春工业大学学报, 2018, 39(5): 470-474. |
| [9] |
冯文斌, 刘宝华. 改进的SIFT算法图像匹配研究. 计算机工程与应用, 2018, 54(3): 200-205, 232. |
| [10] |
Ren DF, Wang QB. An improved SIFT matching algorithm for multi-source satellite images with multiple similar contents. Proceedings of 2014 International Conference on Remote Sensing and Smart City (RSSC2014). Shenzhen, China. 2014. 229–235.
|
| [11] |
Zhang HJ, Hu Q. Fast image matching based-on improved SURF algorithm. Proceedings of 2011 International Conference on Electronics, Communications and Control. Ningbo, China. 2011. 1460–1463.
|
| [12] |
张文卿, 李为相, 李为, 等. 改进的SURF特征快速匹配算法. 计算机工程与设计, 2019, 40(12): 3526-3532. |
| [13] |
马海波, 张鹏程, 张权, 等. 基于二维熵的快速SIFT图像匹配方法. 中北大学学报(自然科学版), 2019, 40(1): 63-69. |
| [14] |
Zhao SJ. Coagulation detection method based on the image information entropy from a new microscopic dew-point hygrometer. Proceedings of 2018 4th International Conference on Green Materials and Environmental Engineering (GMEE 2018). Beijing, China. 2018. 65–72.
|
| [15] |
Huang YK, Jin WD, Li B, et al. Automatic modulation recognition of radar signals based on Manhattan distance-based features. IEEE Access, 2019, 7: 41193-41204. DOI:10.1109/ACCESS.2019.2907159 |
| [16] |
刘星毅, 韦小铃. 基于欧式距离的最近邻改进算法. 广西科学院学报, 2010, 26(4): 409-411. |
| [17] |
程玉胜, 汪辉, 李雨, 等. 基于熵值优化的图像感兴趣区域提取改进方法. 安庆师范学院学报(自然科学版), 2017, 23(3): 48-52. |
| [18] |
Dong KK, Hu MZ. A new parallel algorithm for image matching based on entropy. Journal of Harbin Institute of Technology (New Series), 2001, 8(4): 399-402. |
| [19] |
Mikolajczyk K, Schmid C. A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630. DOI:10.1109/TPAMI.2005.188 |
 2020, Vol. 29
2020, Vol. 29



