2. 武汉大学 计算机学院, 武汉 430072
2. School of Computer Science, Wuhan University, Wuhan 430072, China
随着医学成像规模的不断扩大和高精度成像技术的不断发展, 处理病理图像的方法越来越多, 为医用图像应用带来了极大的便利. 例如当前已提出的病灶检测、肺部分割[1]等多种方法, 已逐渐应用于临床图像诊断. 病例诊断图像不仅需要直观呈现器官轮廓, 同时对纹路清晰度的要求也十分严格. 依靠传统的图像处理方法很难实现对图像的精准处理, 并且需要大量的时间和精力. 随着大数据、云计算技术的飞速发展, 如何快速有效地利用相关技术优势对临床诊断图像进行处理, 已成为一个热点话题. 在此背景下提出了基于稀疏理论与快速有限剪切变换的医学图像融合算法.
日趋成熟的大数据技术[2,3]在分析处理相关数据时具有快速而精准的优势, 当前该技术已广泛运用于用户行为识别、各种数据流量分析等技术领域. 近年来, 为了解决大规模集群数据的内存计算问题, 人们在海量数据处理领域引入了弹性数据集(Resilient Distributed Dataset, RDD)的概念[4-6], 并提供了基于Java、Python和Scala等语言的API, 实现与其他系统的完美结合, 以此来提高图像处理效率.
快速有限剪切波变换[7]在图像处理过程中优势明显, 应用起来也十分简便. 剪切波变换[8]是一种多尺度几何分析的工具, 近几年来逐渐成为研究热点. 剪切波变换克服了传统方向表达能力的缺点, 采用特有的方法可同时处理连续数据和离散数据. 结合剪切变换的特点, 快速有限剪切变换在图像处理方面的能力更强, 然而处理低频系数的能力却几乎为零, 若直接对图像进行处理, 则会造成无法获取最佳图像信息的结果.
在图像融合过程中, 由于高低子带系数的不同, 处理方法也有差异, 研究人员逐渐将目光转向稀疏理论[9]. 比如Shahdoosti[10]、Yu[11]等将稀疏理论运用到图像融合中, 并结合数据字典, 大大提高了子带系数的稀疏度. 因此, 将稀疏理论与快速有限剪切变换有效融合, 可以同时处理高频和低频子带系数, 提高图像处理效率和图像清晰度, 达到医学诊断的需求.
基于以上分析, 本文提出了将稀疏理论和快速有限剪切变换相结合, 对医用诊断源图像进行处理的研究方案. 首先, 采用快速有限剪切波(FFST)[12]分解源图像, 将其分解为高频系数和低频系数两部分; 其中, 高频子带含有源图像细节的重要信息, 低频子带则是源图像的近似图像; 其次, 根据高频和低频系数的不同性质, 提供不同的融合策略, 通过相对标准差比较法[13]对高频系数进行处理; 然后, 对于稀疏性差的低频系数利用K-SVD方法[14]进行训练, 得到数据字典并采用稀疏原理做相应处理; 最后, 将融合后的高频和低频系数通过FFST逆变换融合到医学图像中, 以获取更加清晰直观的图像效果.
1 快速有限剪切波变换和稀疏理论 1.1 快速傅里叶变换快速傅里叶变换[15]是1965年由J.W.库利和T.W.图基提出的. 快速傅里叶变换(FFT)是指利用计算机来计算离散傅里叶变换(DFT)的快速、高效计算方法的统称[16]. 采用这种算法可以使计算离散傅里叶变换所需要的乘法次数大大减少, 特别是被变换的抽样点数N越多, 那么FFT算法计算量就越少. FFT根据离散傅里叶变换的奇、偶、虚、实等特性, 对离散傅立叶变换进行改进所得而来.
根据图像亮度变换剧烈程度不同, 图片可分为高频、中频和低频3种类型. 图像中强度(亮度/灰度)变换平缓的属于低频图像, 高频图像则是图像强度变化较为剧烈, 中频图像亮度变换剧烈程度处于低频图像和高频图像二者之间. 傅里叶变换根据正弦函数来进行判别, 如果在一个变换周期内, 频率变高, 则是高频子带系数; 否则是低频子带系数. 对式(1)进行傅里叶变换, 得:
| $ \varphi \left( {{{{y}}_1},{y_2}} \right) = {\varphi _1}({y_1})\varphi \left(\dfrac{{{y_2}}}{{{y_1}}}\right) $ | (1) |
相应的傅里叶变换的公式为:
| $ \begin{split} {\varphi _{h,j,l}}(w) &= \varphi \left( {B_{{b_h}}^{\rm T}R_{{r_{h,j}}}^{\rm T}} \right){e^{ - 2\pi i\langle y,{t_{{l}}}\rangle }} \\ &={\varphi _1}({4^{ - h}}{y_1}){\varphi _2}\left({2^h}\frac{{y2}}{{y1}} + j \right){e^{ - 2\pi i\langle y,\left( {\frac{{{l_1}}}{L},\frac{{{m_1}}}{M}} \right)\rangle }},w \in \delta \end{split} $ | (2) |
其中,
剪切波变换(Shearlet Transform)是继FFT变换后又一高效的算法, 其将一个基函数进行剪切、缩放和平移等操作并以小波理论为基础进行仿射变换来构造不同特性函数的模型[17].
其公式可以表示为:
| $ {\varphi _{{\rm{b}},r,t}} = {{{b}}^{ - 3/4}}\varphi \left( {B_b^{ - 1}R_r^{ - 1}(x - t)} \right){\rm{ = }}{{{b}}^{ - 3/4}}\varphi \left( {\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{b}}}}&{{\rm{ - }}\dfrac{{{r}}}{{{b}}}}\\ 0&{\dfrac{1}{{\sqrt b }}} \end{array}} \right]{{(x - t)}}} \right) $ | (3) |
其中, b为尺度参数, r为剪切参数, t为平移参数.
剪切波理论可以用来表征除二维以外的其他高维度曲线的特性, 极大地弥补了小波变换的缺点. 令
| $\left\{ \begin{split} &\left\{ {\left( {\frac{{{l_1}}}{L},\frac{{{m_1}}}{M}} \right);({l_1},{m_1}) \in \tau } \right\}\\ &\tau = \{ ({l_1},{m_1}) ;\;{l_1} = 0,\cdots,L - 1;\;{m_1} = 0,\cdots,M - 1\} \end{split}\right. $ | (4) |
将b、r、t分别离散化以加强变换速率, 其公式如下:
| $ \left\{ {\begin{array}{l} {{{{b}}_h} = {2^{ - 2h}} = \dfrac{1}{{4h}},\;h = 0,1,\cdots,{h_0} - 1} \\ {{r_{h,j}} = j{2^{ - h}}, \;- {2^h} < {{j}} < {2^h}} \\ {{t_l} = \left( {\dfrac{{{l_1}}}{L},\dfrac{{{m_1}}}{M}} \right),\;l \in \tau } \end{array}} \right. $ | (5) |
稀疏理论作为图像处理及其应用领域中的不可或缺的一部分, 其实质是用稀疏的系数来简洁地表示原始信号. 稀疏表示是存储和记录图像中基本的关键信号即原子, 用其较少的线性组合来表示大部分或者全部的原始信号. 稀疏表示是原子数目最少的表示形式, 其基本识别原理可以如下表示.
设共有m个类, 每个类下的单个样本用矩阵D中的一个列向量di,j来表示. 如果第i个类包含n个样本, 则:
| $ {{{D}}_{{i}}} = [{d_{i1}},{d_{i2}},\cdots,{d_{i{n_{\rm{i}}}}}] \in {R^{m \times {n_{{i}}}}},D = [{D_1},{D_2},\cdots,{D_m}] $ | (6) |
若x属于第个i类, 则:
| $ {{x}} = {\gamma _{i1}}{d_{i1}} + {\gamma _{i2}}{d_{i2}} + \cdots + {\gamma _{i{n_{{i}}}}}{d_{i{n_{{i}}}}} $ | (7) |
即x可以由第i个类的样本进行线性组合来表示, 也就是已知D和x, 可求出γ, 即:
| $ {\gamma _{{i}}} = \arg {\min _\gamma }\left\| {{x_i} - {D_{(k - 1)}}\gamma } \right\|_2^2,\; {\rm{s.t.}}\;{\left\| a \right\|_0} \ll {L_0} $ | (8) |
再结合K-SVD算法训练完备字典, 使构建出的学习字典能够对稀疏度不同的领域进行稀疏表示, 一次即可提取图像中的相关特征.
2 稀疏理论与快速有限剪切波变换融合算法稀疏理论与快速有限剪切波变换融合策略主要分为3步.
首先, 采用快速傅里叶变换(FFST)分解源图像, 将其分解为高频系数和低频系数两部分. 其中, 高频子带含有源图像细节的重要信息, 低频子带则是源图像的近似图像.
其次, 根据高频和低频系数的不同性质, 选择不同的融合策略. 使用相对标准差比较法对高频系数进行处理; 对于稀疏性差的低频系数, 其包含了源图像的大量能量, 为提高其稀疏度, 引用稀疏理论, 利用K-SVD方法进行训练, 得到字典并采用稀疏原理进行处理.
最后, 将融合后的高频和低频系数通过FFST逆变换融合到医学图像中, 以获取更清晰的效果.
融合算法具体流程如图1所示. 源图像通过FFST进行分解, 分解为高频子带系数和低频子带系数; 高频子带系数通过高频融合规则进行融合, 而低频子带系数则通过训练得到字典, 结合稀疏理论进行处理, 得到融合后的低频子带系数; 最终通过FFST逆变换得到最终融合图像.
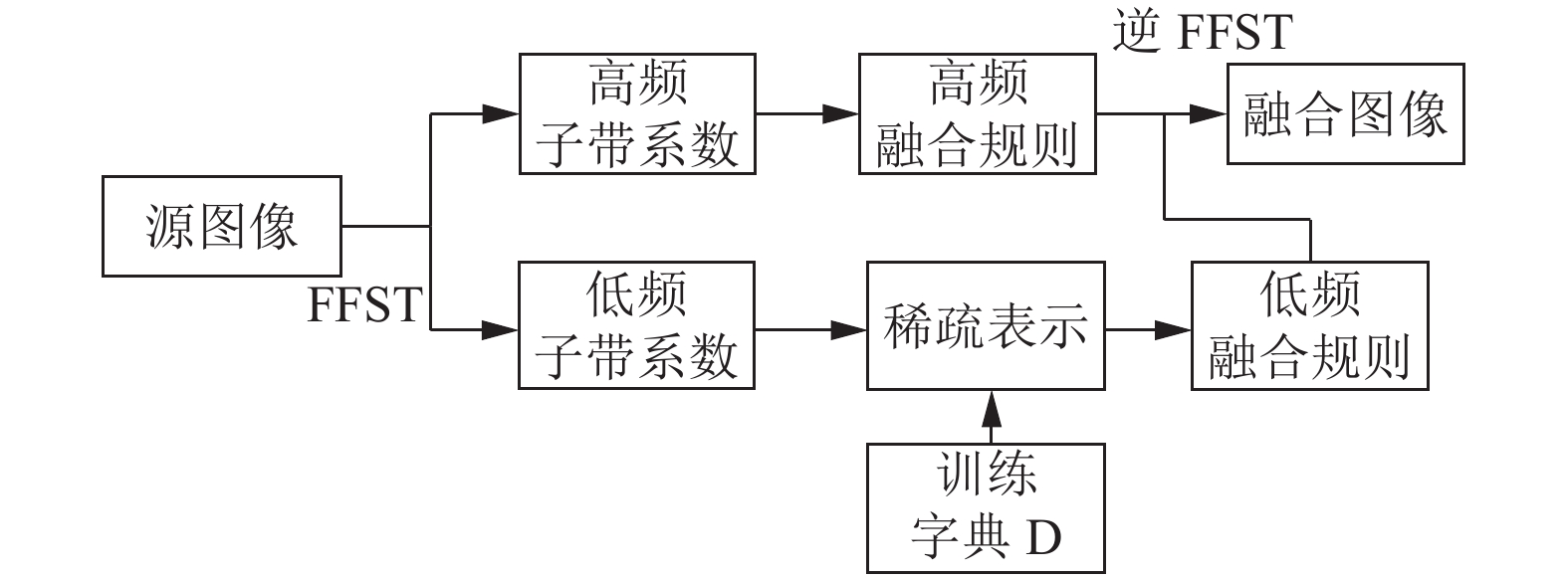
|
图 1 融合过程示意图 |
2.1 高频子带系数的融合策略
在医学界, 为了防止错误诊断, 对于图片处理的要求极其严苛, 尤其是对图像的边缘部位, 处理效果越清晰越好. 然而传统处理方法大多模糊不清, 有时还存在边缘带撕裂等问题. 为了解决上述问题, 引用了文献[18]的相对标准差比较法, 该方法在处理图像边缘时相对于传统方法效果更清晰, 弥补了传统方法的不足, 其具体步骤如下:
1) 取源图形A的区域高频系数
2) 求解
| $ {{{S}}^{l,k}}(i,j) = \left[F_1^{l,k}(i,j) - F_2^{l,k}(i,j)\right]/F_1^{l,k}(i,j) $ | (9) |
为了便于快速计算, 将窗口大小设为3×3, 则
3) 计算
4) 求出
| ${{T = }}\frac{1}{{56}}\left[ {\begin{array}{*{20}{c}} 1&2&1 \\ 2&4&2 \\ 1&2&1 \end{array}} \right]$ |
5) 综合判断
在低频子带系数中, 主要集中的是图像的轮廓信息. 使用梯度加权法、取大方差法等传统方法处理图像时, 所得图像的轮廓会相对比较清晰. 但随着医学诊断需求的不断发展, 使用传统方法处理所得图像的清晰度已逐渐不能满足日常诊断需要. 本文提出的稀疏理论在处理图像稀疏度时效果明显提高, 对图像清晰、轮廓分明等方面也有明显改善, 其具体方法如下:
1) 利用式(5)中的FFST变换分解源图像A, 得到低频子带系数
2) 求解
3) 根据K-SVD算法对
将上述处理后的图像进行融合, 具体步骤如下:
1) 将得到的高频子带系数和低频子带系数分别记为
2) 利用K-SVC算法训练低频子带, 并利用OMP算法进行预估, 最后得到
3) 高频子带运用相对比较差进行融合, 得到高频系数
4) 最后利用逆FFST, 将图像进行融合, 并根据相应指标对其进行判断和分析.
3 仿真实验及结果分析为了验证算法在图像检测应用中的实用性, 选择了3组算法进行对比, 并根据标准差(SD)、空间频率(SF)、结构相似(SSIM)指标[19]等参数对图像进行评价, 一般情况下, 这些指标系数越高说明图像融合效果就越好. 为了让算法的有效性更加具有说服力, 本文将所有实验均在Windows 10操作系统和Matlab 2013环境下进行仿真.
实验选择了2组尺寸大小为512×512的源图像进行仿真, 如图2及图3所示.
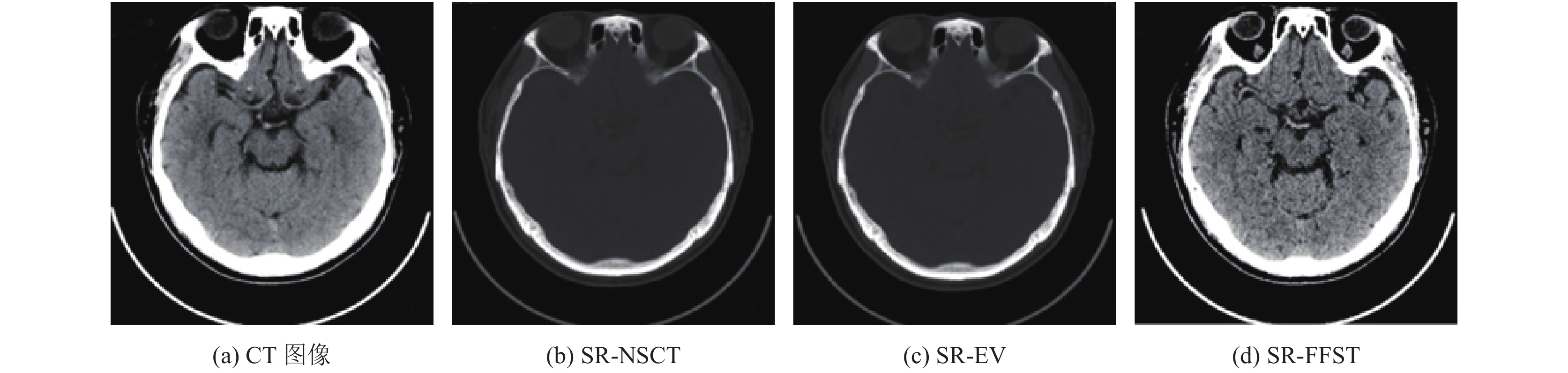
|
图 2 多发性脑梗塞CT/融合图像 |
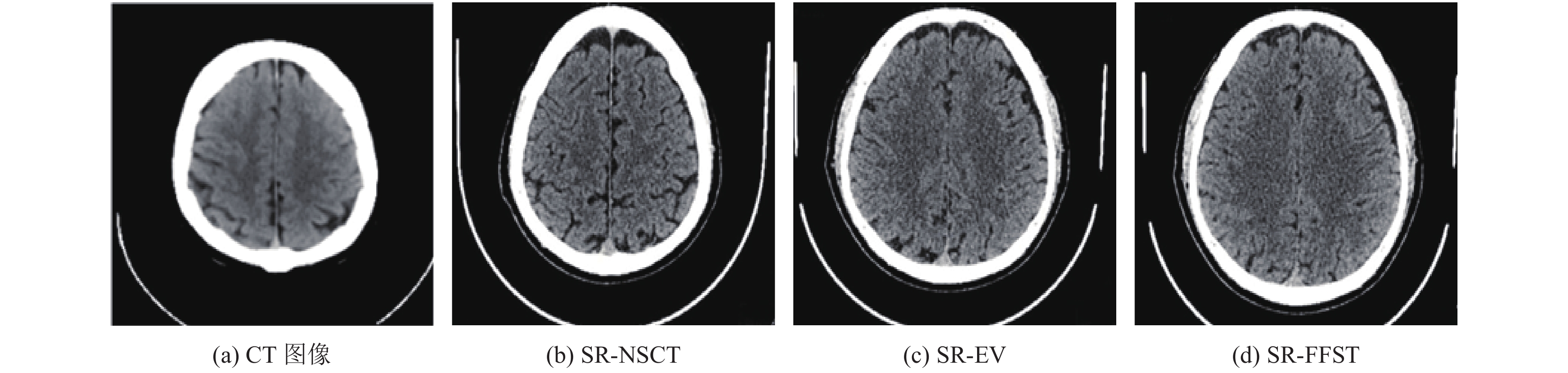
|
图 3 脑卒患者的CT/融合图像 |
图2(a)~图2(d)分别为多发性脑梗塞图; 图3(a)~图3(d)表示脑卒患者的脑部CT图. 图2(a)、图3(a)图像表示CT下的图像; 图2(b)、图3(b)是利用文献[20]提出的低频系数结合稀疏理论(SR-NSCT), 再根据点火次数选择高频系数进行处理所得; 图2(c)、图3(c)是利用文献[21]提出的对高频系数采用激励向量值生成神经网络的方法(SR-EV)以及对低频系数绝对值及其权重进行综合处理所得结果; 图2(d)、图3(d)是利用本文算法(SR-FFST)得到的图像.
从图2和图3可以看出, 本文算法在处理图像的亮度、对比度、清晰度、视觉效果及纹理边缘清晰度等方面均明显高于其他图像, 尤其是边缘纹理的细节特征更加清晰地得以展现.
对上述图像进行3种指标的技术分析, 得到的相关指标参数结果如表1、表2所示.
| 表 1 图2中不同融合算法的相关融合指标 |
| 表 2 图3中不同融合算法的相关融合指标 |
从表1、表2所示结果可知, 文献[20,21]算法的融合指标偏低, 不突出, 融合效果差. 例如, 表1、表2中本文算法的SD值均比较低, 这说明该算法在处理图像时, 得到的图像边缘比较模糊; 而表1、表2中本文算法的指标均占优势, 表明该算法在处理图像时表现良好, 具有较高的处理能力, 同时也验证了本文算法的有效性和优越性.
4 总结图像融合技术的不断发展与提高对医学诊断领域产生了极大的促进, 为改善人们的健康水平提供技术保障. 本文提出的基于稀疏理论与快速有限剪切变换的医学图像融合算法有效解决了处理诊断图片时边缘不清晰、视觉效果差等问题, 结合其他算法案例, 为对比相关指标多次进行仿真实验, 结果表明, 本文算法处理所得的图片清晰度、亮度、边缘清晰度与其他算法相比, 均具有一定的优越性.
| [1] |
焦庆磊, 陈宇彤, 朱明. 融合位置尺度信息的胸部X光肺结节检测. 小型微型计算机系统, 2019, 40(6): 1324-1329. |
| [2] |
陈曦. 视频图像处理技术在安防行业的应用. 电子技术与软件工程, 2019(3): 61. |
| [3] |
陈博恒. 基于特征编码与深度学习的图像识别算法[博士学位论文]. 广州: 华南理工大学, 2018.
|
| [4] |
彭翔. 分布式流处理的铁道供电监控大数据集群容错技术研究[硕士学位论文]. 上海: 华东交通大学, 2018.
|
| [5] |
艾玮. 云计算环境下大规模文本挖掘并行处理技术研究[博士学位论文]. 长沙: 湖南大学, 2017.
|
| [6] |
马宁. 大数据在视频图像信息分析中的运用. 法制博览, 2018(36): 281, 280. |
| [7] |
朱达荣, 许露, 汪方斌, 等. 基于快速有限剪切波变换与引导滤波的多聚焦图像融合算法. 激光与光电子学进展, 2018, 55(1): 011001. |
| [8] |
Zhang L, Tang JT. Seismic data denoising via shearlet transform and data-driven tight frame. Acta Geologica Sinica-English Edition, 2019, 93(S1): 298-299. DOI:10.1111/1755-6724.14105 |
| [9] |
Wang YL, Tang YY, Li LQ, et al. Block sparse representation for pattern classification: Theory, extensions and applications. Pattern Recognition, 2019, 88: 198-209. DOI:10.1016/j.patcog.2018.11.026 |
| [10] |
Shahdoosti HR, Khayat O. Image denoising using sparse representation classification and non-subsampled shearlet transform. Signal, Image and Video Processing, 2016, 10(6): 1081-1087. DOI:10.1007/s11760-016-0862-0 |
| [11] |
Yu NN, Qiu TS, Bi F, et al. Image features extraction and fusion based on joint sparse representation. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 1074-1082. DOI:10.1109/JSTSP.2011.2112332 |
| [12] |
方云录. 基于容量评估与径向和谐傅里叶矩的图像水印算法. 电子测量与仪器学报, 2018, 32(6): 139-147. |
| [13] |
Song Y, Liu Y, Gao QX, et al. Euler label consistent K-SVD for image classification and action recognition. Neurocomputing, 2018, 310: 277-286. DOI:10.1016/j.neucom.2018.05.036 |
| [14] |
Yazdi SV, Douzal-Chouakria A. Time warp invariant kSVD: Sparse coding and dictionary learning for time series under time warp. Pattern Recognition Letters, 2018, 112: 1-8. DOI:10.1016/j.patrec.2018.05.017 |
| [15] |
陈晋. 快速傅里叶变换的研究. 黑龙江科学, 2018, 9(24): 62-63. |
| [16] |
蒋燕, 范恩. 基于非下采样剪切波变换域的图像增强方法. 控制工程, 2018, 25(11): 2022-2026. |
| [17] |
Dalrymple B. Fast fourier transform: A Niche, but critical strategy in optimizing impression evidence. Journal of Forensic Science and Medicine, 2018, 4(4): 192-196. DOI:10.4103/jfsm.jfsm_35_18 |
| [18] |
李晓军, 戴文战, 李俊峰. 结合稀疏理论与非下采样剪切波变换的多模态医学图像融合算法. 浙江理工大学学报(自然科学版), 2018, 39(6): 723-731. |
| [19] |
邓杰航, 毋鹏杰, 余汉君, 等. 基于扩展梯度算子的结构相似度图像质量评价方法. 科学技术与工程, 2018, 18(27): 42-47. |
| [20] |
陈轶鸣. 基于稀疏表示图像融合算法的研究及应用[硕士学位论文]. 南京: 南京信息工程大学, 2018.
|
| [21] |
潘辑, 王雷, 徐韶华. 高频彩色多普勒超声对血液透析患者继发甲状旁腺功能亢进的临床研究. 吉林医学, 2017, 38(10): 1862-1863. |
 2020, Vol. 29
2020, Vol. 29



